Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Curvas de los Límites Norte y Sur del Eclipse Total Central
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo de las Curvas de los Límites Norte y Sur del Eclipse Total Central
[editar]
Sabiendo que la Conjunción Sol-Luna, en Ascensión Recta, ocurre a las 19:21:36 hs. (GMT = Greenwich Meridian Time), tomamos 7 horas para los cálculos respectivos. T₀ = 19 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para las tablas para ±3 hs. a partir de esa T₀, es decir para las 16 hs., 17 hs., 18 hs., 19 hs., 20 hs., 21 hs. y 22 hs. (GMT).
Según los tiempos del primer y último contacto del Eje de Cono de la Sombra Lunar o del punto Z con el horizonte (tangente), que se han hallado en el capítulo Comienzo y Fin del Eclipse Total Central, se comienzan los cálculos desde las 18 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 20,8 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
En este capítulo calcularemos todos los puntos de las curvas correspondientes a los límites Norte y Sur del Eclipse Total Central que se dan, en ambos casos, en los contactos interiores de la Luna con el Sol (ver imagen debajo). Notar que calcularemos las mismas fórmulas del capítulo Curva del Eclipse Total Central. Eclipse Máximo y Ancho de la Sombra y que van desde la (173) a la (184).
Comenzamos entonces, con esta repetición, con γ y en [°]
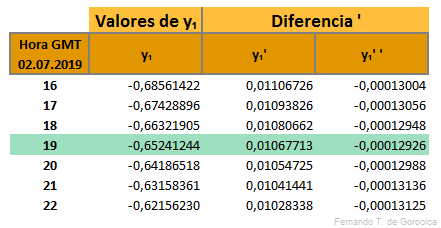
- γ = Atan(x / y₁) (173)
el ángulo γ debe estar comprendido entre 0° y 360°. Si y₁ es negativo sumar 180° a γ.
Luego β en [°]
- β = Aseno(x / Seno(γ)) (174)
el ángulo β debe estar comprendido entre 0° y 360°.
Ahora calcular C en [°] y c
- C = Atan(y₁ / Coseno (β)) (175)
el ángulo C debe estar comprendido entre 0° y 360°. Si Coseno (β) es negativo sumar 180° a C, luego calcular c según C
- c = y₁ / Seno (C) (176)
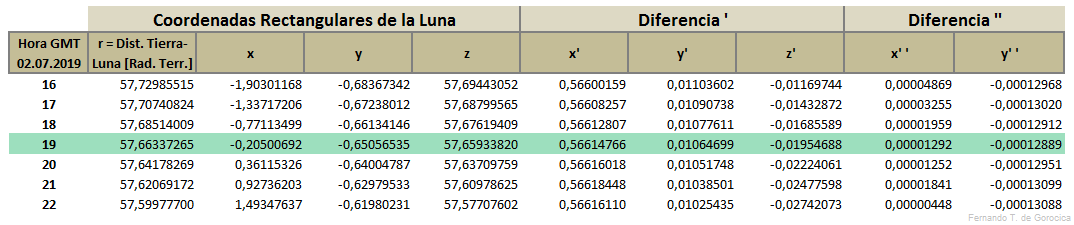
Hallar luego el valor de d en [°], siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también d₁ en [°] siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (177)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Seguido calculamos θ que es el ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar o bien en la Longitud ω, que es aproximadamente el Ángulo Horario del Sol, y correspondiente también a ese instante Tᵢ, entonces
- θ = Atan(x / (c * Coseno(C + d₁))) (178)
el ángulo θ debe estar comprendido entre 0° y 360°, si (c * Coseno(C + d₁)) es negativo (-) sumar 180° a θ. Para el Tiempo Aparente Local que es aproximadamente la Hora Solar Verdadera, dividir θ por 15.
Luego calculamos φ₁ en [°] para hallar después la latitud geográfica φ también en [°]
- φ₁ = Acoseno(c * Seno(C + d₁)) (179)
Después los valores de L y a, primero interpolando, en las tablas correspondientes (más abajo), los valores l₂, i₂, b' , c₂' y f para el instante en cuestión y según las siguientes fórmulas se tiene
- L = Abs(l₂ - i₂ * Coseno(β)) (180)
- a = c₂' - f * Coseno(β) (181)
el valor de f, de ésta última fórmula, lo hallamos en la tabla E, e, F y f (más abajo).
Con las formulas anteriores encontraremos ahora el valor Q en [°]
- Q = Atan(a / b') (182)
el ángulo Q debe estar comprendido entre 0° y 360°. Si b' es negativo (-) sumar 180° a Q.
Por último, hallaremos las coordenadas terrestres para el instante Tᵢ, pero primero μ₁, siendo el ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en Greenwich, ángulo comprendido entre 0° y 360°, para el instante Tᵢ interpolando [1] en la tabla correspondiente (más abajo).
Entonces, para el punto de la curva del Eclipse Total Central para ese instante Tᵢ tenemos:
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) (183) |
| Longitud ω (al W) = μ₁ - θ (184) |
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
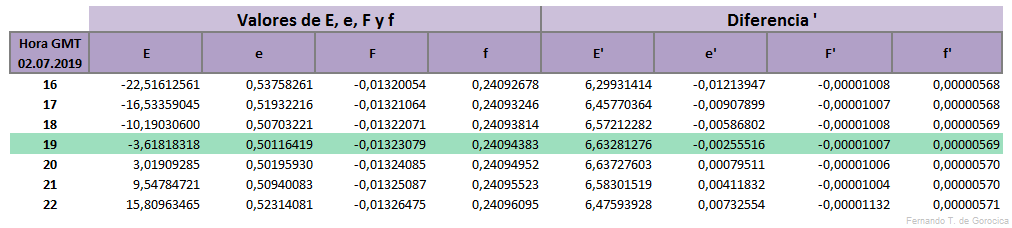
Ahora hallar el valor de E en [°], por medio de la interpolación [1] en la correspondiente tabla (más abajo), seguido el valor de ν' también en [°]
- ν' = Atan((f / e) * Coseno(β)) (213)
los valores de f y e se encuentran interpolando [1] en la tabla correspondiente (más abajo).
Luego calcular Q en [°] según
- Q = Atan(Tan(45 + ν') * Tan(E / 2)) + E / 2 (214)
Después calcular λ en [']
- λ = (l₂ / Seno(1 / 60)) / Coseno(β) - (ι₂ / Seno(1 / 60)) (215)
Ahora H en [°]
- H = Atan(Coseno(Q) / (Seno(Q) * Seno(d₁))) (216)
el ángulo H debe estar comprendido entre 0° y 180°. Si (Seno(Q) * Seno(d₁)) es negativo sumar 180° a H para que luego h sea positivo (+).
Luego h
- h = Coseno(Q) / Seno(H) (217)
después las derivadas de la latitud geográfica φ y de la longitud ω ambas en [']
- dφ = λ * h * Seno(θ - H) (218)
- dω = λ * [h * Coseno(θ - H) * Tan(φ₁) + Seno(Q) * Coseno(d₁)] (219)
Finalmente, las coordenadas terrestres ambas en [°] y para a ese instante Tᵢ tenemos:
para el punto de la curva del Límite Norte del Eclipse Total Central
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) + dφ / 60 (220) |
| Longitud ω (al W) = μ₁ - θ + dω / 60 (221) |
para el punto de la curva del Límite Sur del Eclipse Total Central
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) - dφ / 60 (222) |
| Longitud ω (al W) = μ₁ - θ - dω / 60 (223) |
En el caso de los Eclipses Anulares los signos en color bordó de estas cuatro últimas fórmulas deben invertirse, es decir los positivos + pasan a ser negativos - y los negativos - en positivos +.
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Ejemplo práctico:
[editar]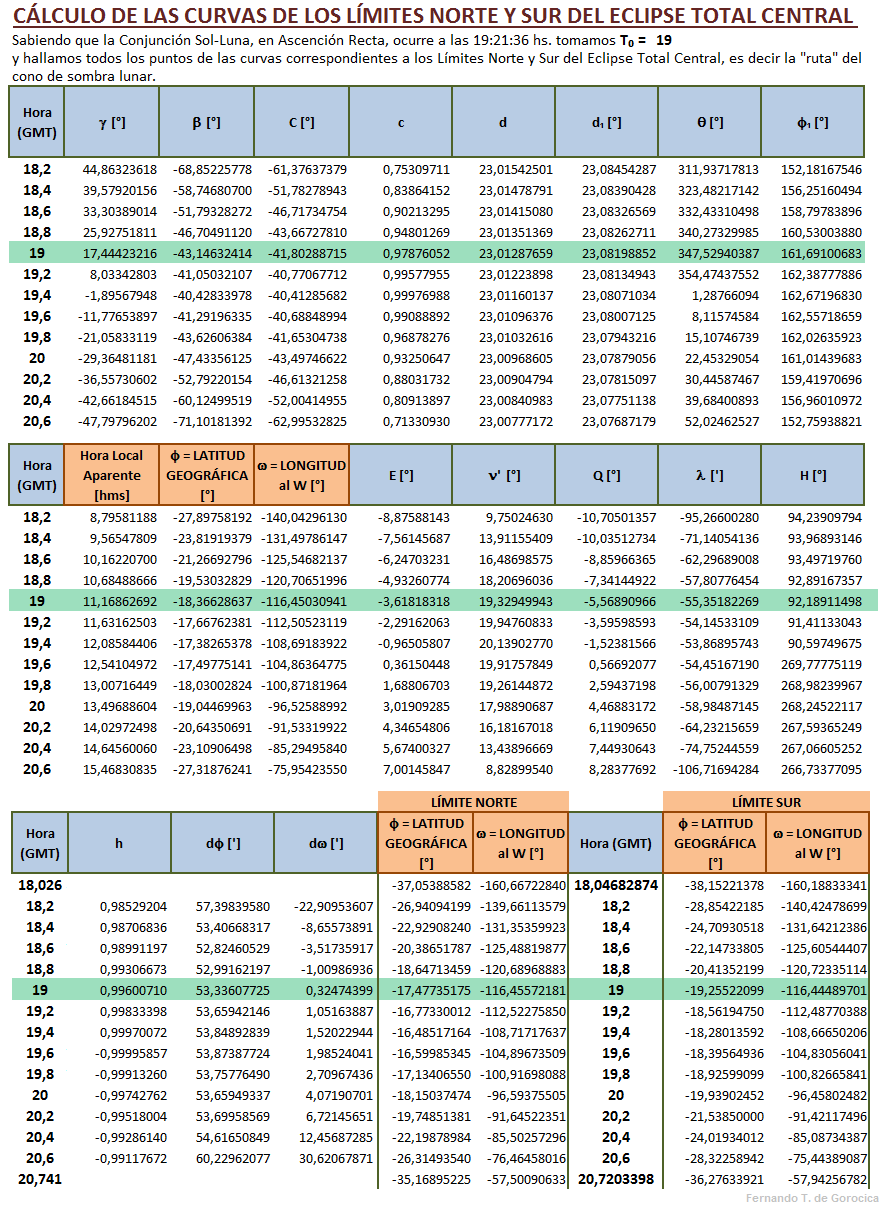
Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |