Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Comienzo y Fin del Eclipse en un Lugar Dado (Ciudad de Buenos Aires)
| Capítulo Anterior | Contenidos |
Cálculo del Comienzo y Fin del Eclipse en un Lugar Dado (Ciudad de Buenos Aires)
[editar]Sabiendo, por la curva de la totalidad (en Longitud terrestre), que el Eclipse Medio en este lugar ocurre poco antes de las 21:00 hs (GMT) tomamos T₀ = 21 hs.
El cálculo del Comienzo y Fin del Eclipse en un Lugar Dado lo realizaremos para observadores ubicados en la Ciudad de Buenos Aires siendo su
| Latitud Geográfica φ = -34,59972222 (224) |
| Latitud Geocéntrica φ' = Atan(Seno(φ) * (1 - e^2) / Coseno(φ)) (225) |
| Longitud ω = 58,381944444 (226) |
| Huso = -3 (227) |
| ρ = 0,99833132881 + 0,0007271 * Coseno(2 * φ) - 0,0000018 * Coseno(4 * φ) (228) |
ρ es la distancia en [Radios Terrestres] desde el centro de la Tierra hasta la Latitud Geográfica φ. e lo encontramos en la tabla de las Constantes (más abajo).
Comenzamos entonces calculando L en [°] donde l₁, i₁ y ζ para T₀ = 21 hs. como primera aproximación, hallando estos valores en las tablas correspondientes (más abajo)
- L = l₁ - i₁ * ζ (229)
Luego calcular M₀ en [°] donde x₀ e y₀ son las Coordenadas Rectangulares de la Luna, ξ y η para T₀ = 21 hs. como primera aproximación, hallando estos valores en las tablas correspondientes (más abajo)
- M₀ = Atan((x₀ - ξ) / (y₀ - η)) (230)
el ángulo M₀ debe estar comprendido entre 0° y 360°. Si (y₀ - η) es negativo sumar 180° a M₀ para que luego m sea positivo (+).
Luego m
- m = (x₀ - ξ) / Seno(M₀) (231)
Calculamos después N₀ en [°] donde x' , y' son las diferencias derivadas de las Coordenadas Rectangulares de la Luna, ξ' y η' también para T₀ = 21 hs., hallando estos valores en las tablas correspondientes (más abajo)
- N₀ = Atan((x' - ξ') / (y' - η')) (232)
el ángulo N₀ debe estar comprendido entre 0° y 180°. Si (y' - η') es negativo sumar 180° a N₀ para que luego n sea positivo (+).
Luego n
- n = (x' - ξ') / Seno(N₀) (233)
Seguido calcular ψ en [°]
- ψ = Aseno(m * Seno(M₀ - N₀) / L) (234)
Luego Δ en [hms]
- Δ = -m * Coseno(M₀ - N₀) / n (235)
Por lo tanto, los Tiempos en [hms (GMT)] del Comienzo y Fin del Eclipse en el lugar de observación (contactos exteriores) serán:
| Comienzo T₁ = T₀ + Δ - L * Coseno(ψ) / n (236) |
| Fin T₂ = T₀ + Δ + L * Coseno(ψ) / n (237) |
donde Coseno(ψ) debe ser tomado con signo tanto (-) como (+), siendo el primero para el comienzo y el segundo para el fin del Eclipse Local (contactos exteriores).
Comenzamos luego con una segunda aproximación, pero primero calcularemos para el Comienzo T₁ y Fin T₂ los valores de τ, argumentos para interpolar [1] en la tabla correspondiente (más abajo) y en los subsiguientes valores a hallar.
Para el comienzo:
- τ = Δ - L * Coseno(ψ) / n (238)
Para el fin:
- τ = Δ + L * Coseno(ψ) / n (239)
Luego calcular θ en [°] para el Comienzo T₁ y Fin T₂ y de ahora en más también para el resto de los valores a hallar
- θ = μ₁ + ω (240)
μ₁ se hallará interpolando en la tabla correspondiente (más abajo) y según el argumento τ hallado anteriormente. El ángulo θ debe estar comprendido entre 0° y 360°.
Seguido calcular B en [°]
- B = Atan(Seno(φ') / (Coseno(φ') * Coseno(θ))) (241)
siendo φ' la latitud geocéntrica en [°], el ángulo B debe estar comprendido entre 0° y 180°. Si (Coseno(φ') * Coseno(θ)) es negativo sumar 180° a B.
luego calcular A
- A = ρ * Seno(φ') / Seno(B) (242)
donde ρ es la distancia en [Radios Terrestres] desde el centro de la Tierra hasta la Latitud Geográfica φ.
Ahora calcular los nuevos valores de ξ, η y ζ entonces
- ξ = ρ * Coseno(φ') * Seno(θ) (243)
- η = A * Seno(B - d) (244)
- ζ = A * Coseno(B - d) (245)
d es la Declinación del Eje del Cono de la Sombra Lunar o del punto Z. Calcularlo para el comienzo y fin interpolando en la tabla correspondiente (más abajo).
Luego los valores ξ' , η' se hallan interpolando en la tabla respectiva (más abajo).
Ahora sí, comenzamos con una segunda aproximación nuevamente desde la fórmula (229) hasta la (237) tanto para el comienzo como para el fin del Eclipse. En el transcurso del cálculo nos dará los tiempos T₁ y T₂ ya ajustados [hms (GMT)]. Recordar que las nuevas interpolaciones se realizarán también con el nuevo argumento de τ actualizado con los nuevos valores recientemente hallados en esta segunda aproximación.
Los nuevos tiempos T₁ y T₂ en [hms (GMT)], del comienzo y fin del Eclipse observado en el lugar dado, llevarlos a la Hora Local según
| Comienzo T₁ = T₁ + Huso (246) |
| Fin T₂ = T₂ + Huso (247) |
donde el Huso es el del lugar de observación (227)
La Hora del Eclipse Máximo o Máximo Oscurecimiento en [hms] (hora local) será
| Hora Local del Eclipse Máximo = T₀ + Δ + Huso (248) |
El Δ debe ser tomado de la primera aproximación, fórmula (235).
Luego calcular φ₁, latitud geográfica corregida en [°]
- φ₁ = Atan(Tan(φ) * (1 - e^2)^0.5) (249)
Para determinar si el primer contacto de la Luna con el Sol (Comienzo), el eclipse máximo local y el último contacto de la Luna con el Sol (Fin) ocurren por encima del horizonte, se dan si 0 <= (ζ₁ * ρ₁ * Sin(φ') / Sin(φ₁)) <= 1, donde φ' lo tomamos de la fórmula (225) y ζ₁ y ρ₁ los hallamos interpolando según las tablas del capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos y para T₁, Hora Local del Eclipse Máximo y T₂.
A continuación, calcular γ en [°] según cada τ, para luego calcular el Ángulo desde el Vértex también en [°]
- γ = Atan((ξ + ξ' * τ) / (η + η' * τ)) (250)
el ángulo γ debe estar comprendido entre 0° y 360°. Si (η + η' * τ) es negativo sumar 180° a γ
También para cada τ, tomamos con el nuevo ψ para el comienzo del Eclipse, es decir el primer contacto exterior
- ψ = 180 - ψ (251)
y 360° + ψ para el fin del Eclipse, es decir el último contacto exterior.
Finalmente, con el nuevo N (232), calculamos el Ángulo desde el Vértex
- Ángulo desde el Vértex = N + ψ - γ (252)
El Ángulo de Posición del Punto de Contacto Luna-Sol contado en sentido antihorario sobre el limbo solar desde el punto Norte Celestial en [°] y para cada τ será
- Ángulo de Posición del Punto de Contacto Luna-Sol = N + ψ (253)
para el 1° contacto Luna-Sol el ángulo debe estar comprendido entre 180° y 360°, para el último contacto Luna-Sol el ángulo debe estar comprendido entre 0° y 180°.
Para el cálculo de la Magnitud del Eclipse Máximo en el Lugar y la Razón Luna/Sol primero calcular ΔSL la distancia angular en [°] desde el centro de la Luna al centro del Sol en el Eclipse Máximo en el lugar con los valores interpolados con el argumento [Hora Local del Eclipse Máximo [h] - Huso - T₀], donde el huso es el del lugar de observación (227), entonces
- ΔSL = ABS(((x - ξ) * (y' - η') - (x' - ξ') * (y - η)) / ((x' - ξ')^2 + (y' - η')^2)^0,5) (254)
Los valores L₁ y L₂ se interpolarán en la tabla correspondiente (más abajo) y también como argumento [Hora Local del Eclipse Máximo [h] - Huso - T₀].
Por último, la Magnitud del Eclipse Máximo en el Lugar en [Fracción del Diámetro Solar] será
| Magnitud del Eclipse Máximo = (L₁ - ΔSL) / (L₁ + L₂) (255) |
William Chauvenet lo llama "Grado de Oscurecimiento" expresado en fracción del diámetro solar (= 1).
Y la Razón Luna/Sol, razón del diámetro de la Luna dividido el diámetro del Sol, será
| Razón Luna/Sol = (L₁ - L₂) / (L₁ + L₂) (256) |
Ejemplo práctico:
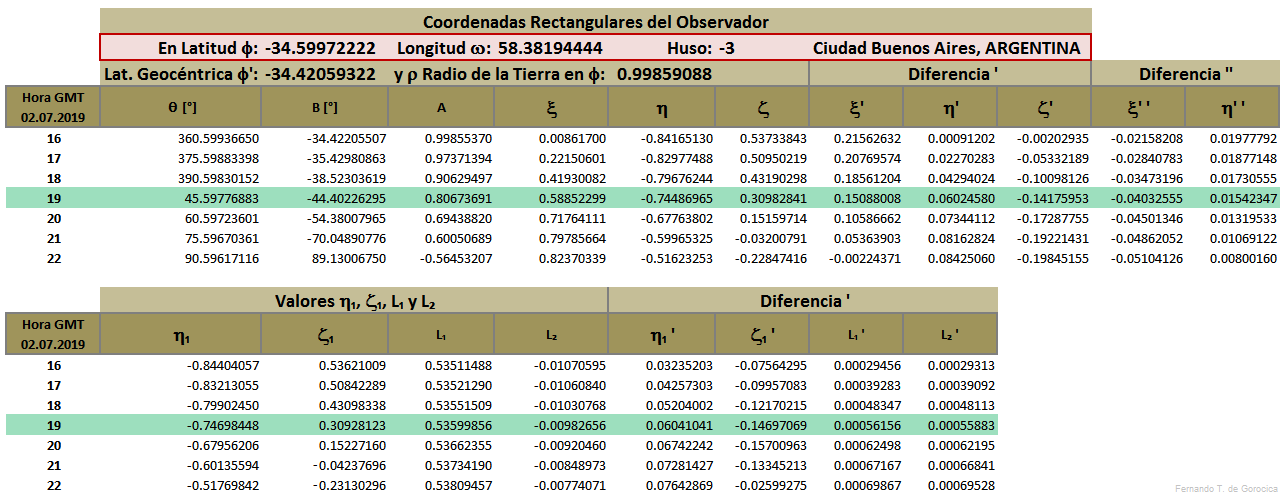
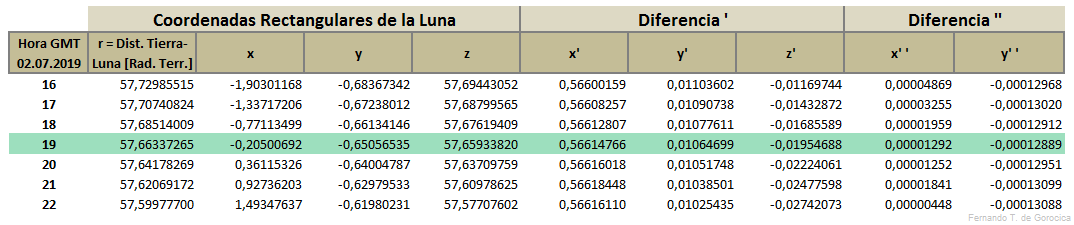
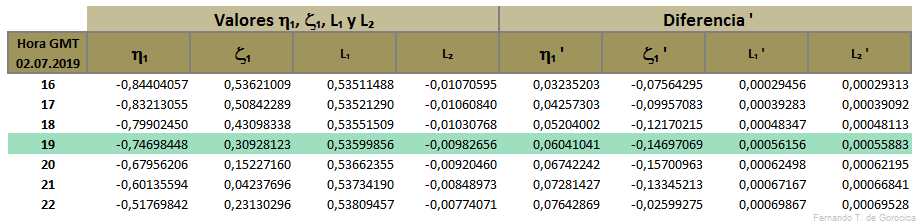
[editar]Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |