Matemáticas/Geometría Analítica/Circunferencia/Ecuaciones de la circunferencia

Ecuación en coordenadas cartesianas

circunferencia de radio dos en un sistema de coordenadas

En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

$(x-a)^{2}+(y-b)^{2}=r^{2}\,$.

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica a

$x^{2}+y^{2}=r^{2}\,$.

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia se deduce que:

$x^{2}+y^{2}+Dx+Ey+F=0\,$

resultando:

$a=-{\frac {D}{2}}$

$b=-{\frac {E}{2}}$

$r={\sqrt {a^{2}+b^{2}-F}}$

Si conocemos los puntos extremos de un diámetro: $(x_{1},y_{1}),(x_{2},y_{2})\,$, la ecuación de la circunferencia es:

$(x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.\,$

Ecuación vectorial de la circunferencia

En el espacio vectorial R², la circunferencia con centro en el origen y radio R, viene dada por la ecuación vectorial:

$\mathbf {r} (\theta )=(R\cos(\theta ),R\operatorname {sen}(\theta ))\,$,

donde $\theta \,$ es el parámetro de la curva, además cabe destacar que $\theta \in [0,2\pi )$. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente x y la componente y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio vectorial R³ esta misma ecuación da como resultado un cilindro, dejando el parámetro z libre.

De manera más general, si c es un punto fijo, x un punto variable cualquiera (ambos de R²) y r un real positivo, la ecuación vectorial

$\|\mathbf {x} -\mathbf {c} \|=r$

representa una circunferencia de centro c y radio r. La doble barra vertical representa la norma vectorial; en este caso corresponde a la distancia euclidiana constante de valor r.

Ecuación en coordenadas polares

Circunferencia unitaria.

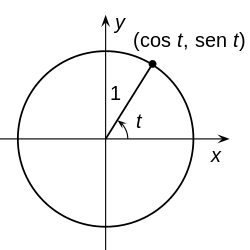
Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como $(r,\theta )\,$

$r=c.\,$

Cuando el centro no está en el origen, sino en el punto $(s,\alpha )\,$ y el radio es $c\,$, la ecuación se transforma en:

$r^{2}-2sr\cos(\theta -\alpha )+s^{2}=c^{2}$

Ecuación paramétrica de la circunferencia

La circunferencia con centro en (a, b) y radio r se parametriza con funciones trigonométricas como:

${\begin{cases}x=&a+r\cos t\\y=&b+r\,\operatorname {sen} t\end{cases}}\qquad t\in [0,2\pi )$

donde t es el parámetro, que varía en el rango indicado. También se puede parametrizar con funciones funciones racionales como

${\begin{cases}x=&a+r\left({\frac {1-t^{2}}{1+t^{2}}}\right)\\y=&b+r\left({\frac {2t}{1+t^{2}}}\right)\end{cases}}\qquad t\in {\widehat {\mathbb {R} }}$

donde t no solo recorre todos los valores reales, sino también un punto en el infinito.

Ecuación en el plano complejo

En el plano complejo, una circunferencia con centro c y radio (r) tiene como ecuación $|z-c|=r\,$. En forma paramétrica puede ser escrita como $z=re^{it}+c$.