Física/Electromagnetismo/Campo Magnético

Fuerza de Lorentz

Entre las definiciones de campo magnético se encuentra la dada por la fuerza de Lorentz. Esto sería el efecto generado por una corriente eléctrica o un imán, sobre una región del espacio en la que una carga eléctrica puntual de valor (q), que se desplaza a una velocidad $\mathbf {(v)}$, experimenta los efectos de una fuerza que es secante y proporcional tanto a la velocidad (v) como al campo (B). Así, dicha carga percibirá una fuerza descrita con la siguiente ecuación.

$\mathbf {F} =q\mathbf {v} \times \mathbf {B}$

donde F es la fuerza magnética, v es la velocidad y B el campo magnético, también llamado inducción magnética y densidad de flujo magnético. (Nótese que tanto F como v y B son magnitudes vectoriales y el producto vectorial tiene como resultante un vector perpendicular tanto a v como a B). El módulo de la fuerza resultante será:

$|\mathbf {F} |=|q||\mathbf {v} ||\mathbf {B} |\cdot \mathop {\operatorname {sen} } (\theta )$

La existencia de un campo magnético se pone de relieve gracias a la propiedad (la cual la podemos localizar en el espacio) de orientar un magnetómetro (laminilla de acero imantado que puede girar libremente). La aguja de una brújula, que evidencia la existencia del campo magnético terrestre, puede ser considerada un magnetómetro.

Fuentes del campo magnético

Un campo magnético tiene dos fuentes que lo originan. Una de ellas es una corriente eléctrica de conducción, que da lugar a un campo magnético estático, si es constante. Por otro lado una corriente de desplazamiento origina un campo magnético variante en el tiempo, incluso aunque aquella sea estacionaria.

La relación entre el campo magnético y una corriente eléctrica está dada por la ley de Ampère. El caso más general, que incluye a la corriente de desplazamiento, lo da la ley de Ampère-Maxwell.

Campo magnético producido por una carga puntual

El campo magnético generado por una única carga en movimiento (no por una corriente eléctrica) se calcula a partir de la siguiente expresión:

$\mathbf {B} ={\frac {\mu _{0}}{4\pi }}{\frac {(q\mathbf {v} )\times {\hat {\mathbf {u} }}_{r}}{r^{2}}}$

Donde $\mu _{0}=4\pi \cdot 10^{-7}{\frac {\mbox{N}}{{\mbox{A}}^{2}}}$. Esta última expresión define un campo vectorial solenoidal, para distribuciones de cargas en movimiento la expresión es diferente, pero puede probarse que el campo magnético sigue siendo un campo solenoidal.

Campo magnético producido por una distribución de cargas

• La inexistencia de cargas magnéticas lleva a que el campo magnético es un campo solenoidal lo que lleva a que localmente puede ser derivado de un potencial vector $\mathbf {A}$, es decir:

$\mathbf {B} =\nabla \times \mathbf {A}$

A su vez este potencial vector puede ser relacionado con el vector densidad de corriente mediante la relación:

$\Delta \mathbf {A} =\mu _{0}\mathbf {j}$

La ecuación anterior planteada sobre $\scriptstyle \mathbb {R} ^{3}$, con una distribución de cargas contenida en un conjunto compacto, la solución es expresable en forma de integral. Y el campo magnético de una distribución de carga viene dado por:

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int _{V_{1}}{\frac {\mathbf {j} _{1}\times \mathbf {\hat {u}} _{r}}{\|\mathbf {r} -\mathbf {r} _{1}\|^{2}}}\ \mathrm {d} V_{1}$

Inexistencia de cargas magnéticas aisladas

Cabe destacar que, a diferencia del campo eléctrico, en el campo magnético no se ha comprobado la existencia de monopolos magnéticos, sólo dipolos magnéticos, lo que significa que las líneas de campo magnético son cerradas, esto es, el número neto de líneas de campo que entran en una superficie es igual al número de líneas de campo que salen de la misma superficie. Un claro ejemplo de esta propiedad viene representado por las líneas de campo de un imán, donde se puede ver que el mismo número de líneas de campo que salen del polo norte vuelve a entrar por el polo sur, desde donde vuelven por el interior del imán hasta el norte.

Ilustración de un campo magnético alrededor de un alambre a través del cual fluye corriente eléctrica.

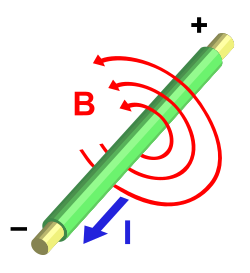
Como se puede ver en el dibujo, independientemente de que la carga en movimiento sea positiva o negativa, en el punto A nunca aparece campo magnético; sin embargo, en los puntos B y C el campo magnético invierte su dirección dependiendo de si la carga es positiva o negativa. La dirección del campo magnético viene dado por la regla de la mano derecha, siendo las pautas las siguientes:

• en primer lugar se imagina un vector qv, en la misma dirección de la trayectoria de la carga en movimiento. La dirección de este vector depende del signo de la carga, esto es, si la carga es positiva y se mueve hacia la derecha, el vector +qv estará orientado hacia la derecha. No obstante, si la carga es negativa y se mueve hacia la derecha, el vector es -qv va hacia la izquierda;
• a continuación, vamos señalando con los cuatro dedos de la mano derecha (índice, medio, anular y meñique), desde el primer vector qv hasta el segundo vector Ur, por el camino más corto o, lo que es lo mismo, el camino que forme el ángulo menor entre los dos vectores. El pulgar extendido indicará en ese punto la dirección del campo magnético.

Energía almacenada en campos magnéticos

La energía es necesaria para generar un campo magnético, para trabajar contra el campo eléctrico que un campo magnético crea y para cambiar la magnetización de cualquier material dentro del campo magnético. Para los materiales no-dispersivos, se libera esta misma energía tanto cuando se destruye el campo magnético para poder modelar esta energía, como siendo almacenado en el campo magnético.

Para materiales lineales y no dispersivos (tales que $\scriptstyle B=\mu H$ donde μ es independiente de la frecuencia), la densidad de energía es:

${\mathcal {E}}_{M}={\frac {B^{2}}{2\mu }}={\frac {\mu H^{2}}{2}}$

Si no hay materiales magnéticos alrededor, entonces el μ se puede substituir por μ₀. La ecuación antedicha no se puede utilizar para los materiales no lineales, se utiliza una expresión más general dada abajo.

Generalmente la cantidad incremental de trabajo por el δW del volumen de unidad necesitado para causar un cambio pequeño del δB del campo magnético es: δW= H*δB

Una vez que la relación entre H y B se obtenga, esta ecuación se utiliza para determinar el trabajo necesitado para alcanzar un estado magnético dado. Para los materiales como los ferromagnéticos y superconductores el trabajo necesitado también dependerá de cómo se crea el campo magnético.