Física/Lo que aprendí leyendo a Feynman - Electromagnetismo/Dentro de los Dielectricos

Dentro de los Dieléctricos

---

En esta seccion veremos porque los materiales son diélectricos. Discutiremos el mecanismo por el cual la polarización se lleva a cabo cuando existe un campo eléctico dentro del material. Empecemos con el ejemplo más sencillo, la polarización de los gases. Se distinguen dos tipos de moleculas de gases, las que no tienen un momento dipolar inherente,llamadas moléculas no-polares, como la molécula de oxídeno,la cuál posee un par de átomos simétricos; y las que si lo tienen, como la molécula del agua, la cual tiene un arreglo no simétrico de entre sus átomos de hidrógrno y oxígeno. A este tipo de moléculas se les llama polares.

Empezaremos discutiendo la polarización de moleculas no-polares. Consideremos un gas monoatómico, como el helio. Cuando un átomo de este tipo es sometido a un campo eléctrico, los electrones son jalados hacia un lado del campo y los nucleos hacia el otro. Esto induce un momento dipolar, que es proporcional al campo eléctrico cuando éste no es muy fuerte. El desplazamiento de la distribución del electrón que produce este tipo de momentos dipolares inducidos es llamado polarización electrónica.

Es posible demostrar que, cuando el átomo es sometido a un campo eléctrico oscilatorio, el centro de carga del electron obedece la ecuación diferencial

$m{\frac {d^{2}x}{dt^{2}}}+mw_{0}^{2}x=q_{e}E$

El primer término es la masa multiplicada por la aceleración, y el segundo es una fuerza restauradora, mientras que el termino del lado derecho es la fuerza que ejerce el campo eléctrico. Esta ecuación tiene la solución

$x={\frac {q_{e}E}{mw_{0}^{2}}}$

Multiplicando esta expresion por la carga del electrón obtenemosel momento dipolar p de un átomo

$p=q_{e}x={\frac {q_{e}^{2}E}{mw_{0}^{2}}}$

Se suele considerar que el momento dipolar es proporcional al campo eléctrico, y se escribe:

${\vec {p}}=\alpha \epsilon _{0}{\vec {E}}$

donde $\alpha$ es una constante con dimensiones $L^{3}$ llamada polarizabilidad del átomo, que nos indica que tan facil es polarizar el átomo en cuestion. Comparando las dos pasadas ecuaciones, obtenemos una expresión para la polarizabilidad

$\alpha ={\frac {q_{e}^{2}}{\epsilon _{0}mw_{0}^{2}}}={\frac {4\pi e^{2}}{mw_{0}^{2}}}$

Si tenemos N átomos por unidad de volumen, la polarización P es dada por

$(*){\vec {P}}=N{\vec {p}}=N\alpha \epsilon _{0}{\vec {E}}$

Recordemos que la polarización es proporcional al campo electrico:

${\vec {P}}=\chi \epsilon _{0}{\vec {E}}$

Expresando esta ecuación en terminos de la constante dielectrica $\kappa$:

$\kappa -1={\frac {P}{\epsilon _{0}E}}$ donde $\kappa =1+\chi$

Igualando esta ultima ecuación con (*) tenemos

$\kappa -1={\frac {P}{\epsilon _{0}E}}={\frac {N}{\alpha }}$

Sutituyendo la polarizabilidad:

$\kappa -1={\frac {4\pi Ne^{2}}{mw_{0}^{2}}}$

Nuestra fórmula es solamente una aproximación, ya que hemos dejado de lado las complicaciones de la mecánica cuántica. Pero veamos que tan buena es nuestra aproximacion calculando $\kappa$, la constante dieléctrica del hidrogeno.

La energía necesaria para ionizar al átomo de hidrógeno es aproximadamente

$E\approx {\frac {me^{4}}{2\hbar ^{2}}}$

Para un estimado de la frecuencia natural $w_{0}$, podemos hacer esta energía igual a $\hbar w_{0}$, la energía de un oscilador atómico cuya frecuencia natural es $w_{0}$. Entonces tenemos:

$w_{0}\approx {\frac {1}{2}}{\frac {me^{4}}{\hbar ^{3}}}$

Sustituyendo este valor para la ecuación de la polarizabilidad tenemos

$\alpha \approx 16\pi [{\frac {\hbar ^{2}}{me^{2}}}]^{3}$

La cantidad ${\frac {\hbar ^{2}}{me^{2}}}$ es el radio de la orbita del estado más bajo en el átomo de Bohr. Ahora, para un gas a presión y temperatura estandar, es decir, 1 atmósfera y 0°C, ahi 2.69x10^19 átomos/cm^3. Entonces resulta ser que

$k\approx 1+(2.69\times 10^{19})16\pi (0.528\times 10^{-8})^{3}=1.0002$

La constante dielectrica para el hidrogeno es medida experimentalmente, y su valor es

$k_{exp}\approx 1.00026$

Felizmente encontramos que la teoría va por buen camino.

Ahora pasemos a las moléculas que tienen un momento dipolar permanente $p_{0}$, como la molécula del agua. En ausencia de campo magnético, los dipolos individuales apuntan en direcciones arbitrarias, produciendo un momento total cero. Cuando se aplica un campo eléctrico, pasan dos cosas: primero, hay un momento dipolar inducido debido a la fuerza sobre los electrones, esta parte da la misma polarizabilidad electrónica que encontramos para moleculas no-polares. Segundo, el campo eléctrico tiende a alinear los dipolos individuales para producir un momento neto por unidad de volumen. Si la alineación fuera perfecta, el momento dipolar sería muy grande, pero eso no sucede ya que, a temperaturas y campos electricos ordinarios las colisiones entre las moléculas evitan este alineamiento. La polarización es calculada mediante métodos de mecánica estadística. Para el uso de este tipo de métodos necesitamos conocer la energía de un dipolo en un campo eléctrico. Consideremos un dipolo con momento $p_{0}$ en un campo eléctrico. Sea $q\phi (1)$ la energía de la carga positiva y $-q\phi (2)$ la energía de la carga negativa. Entonces la enrgía del dipolo es

$U=q\phi (1)-q\phi (2)=q{\vec {d}}\cdot {\vec {\nabla }}\phi$

$U=-{\vec {p}}_{0}\cdot {\vec {E}}=-p_{0}Ecos(\theta )$

A partir de la mecánica estadística se sabe que, en estado de equilibrio térmico, el número relativo de moléculas con energía potencial U es proporcional a

$e^{\frac {-U}{kT}}$

Ahora, sea $n(\theta )$ el número de moléculas por unidad de ángulo sólido en $\theta$, tenemos

$n(\theta )=n_{0}e^{p_{0}Ecos\theta /kt}$

Para temperaturas y campos de magnitud normal, el exponente es un número pequeño, entonces, podemos exandir el exponencial en una serie para obtener

$n(\theta )=n_{0}(1+{\frac {p_{0}Ecos\theta }{kT}})$

Podemos encontrar $n_{0}$ si integramos esta expresión sobre todos los ángulos, el resultado debe ser N, el número total de moleculas por unidad de volúmen. El valor promedio de $\theta$ sobre todos los angulos es cero, entonces la integral es sólo $n_{0}$ multiplicado por el ángulo sólido $4\pi$

$n_{0}={\frac {N}{4\pi }}$

Ahora, para calcular la polarización P necesitamos el vector suma de todos los momentos de las moléculas en una unidad de volúmen. Como sabemos que el resultado será en la dirección de E, sumaremos sólo las componentes en esa dirección (las componente en angulos rectos sumarán cero):

$P=\sum p_{0}cos\theta _{i}$

Podemos evaluar esta suma integrando sobre la distribución de angulos. El angulo sólido en $\theta$ es $2\pi sin\theta d\theta$, entonces

$P=\int _{0}^{\pi }n(\theta )p_{0}cos\theta 2\pi sin\theta d\theta$

Sustituyendo la expresion que habíamos encontrado un poco antes para $n(\theta )$

$P=-{\frac {N}{2}}\int _{0}^{\pi }(1+{\frac {p_{0}Ecos\theta }{kT}})p_{0}cos\theta d(cos\theta )$

$P={\frac {Np_{0}^{2}E}{3kT}}$

La polarización es normal al campo electrico, por lo que hay comportamiento de un dieléctrico normal, además, P depende inversamente de la temperatura, ya que a temperaturas más altashay más desalineación por las colisiones. Esta dependencia de 1/T es llamada ley de Curie. Vemos que $p_{0}$ aparece elevado al cuadrado, esto se debe a que, en un campo electrico dado la fuerza de alineación depende de $p_{0}$, y el momento medio que se produce por esta alineación es otra ves proporcional a $p_{0}$. El momento inducido promedio es proporcional al cuadrado de este momento dipolar permanente.

Campos eléctricos en cavidades de dieléctricos

Consideremos ahora el problema de la constante dieléctrica en la materia densa. Supón que tenemos helo líquido, o argón liquido. Esperamos que halla polarización, pero esta ves P puede ser muy grande, ya que el campo sobre un átomo individual se ve influenciado por la polarización de los átomos vecinos a éste. Nos hacemos la siguiente pregunta: ¿Qué campo eléctrico actúa en el átomo individual?

Si ponemos el líquido entre las placas de un condenador cargado, existirá un campo eléctrico que será la suma del campo del condensador mas el campo producido por las cargas de los átomos. Ignorando las pequeñas variaciones, diremos que el campo eléctrico promedio es $E={\frac {V}{d}}$ donde d es la distsncia de separación entre las placas y V la diferncia de potencial entre ellas. Podríamos pensar que un átomo promedio en una localización promedio sentirá este campo promedio, pero no es así. Consideremos hoyos con diferentes formas en el diélectrico. Supon primero que cortamos un hoyo como en la figura (a), la integral de linea del campo electrico sobre la curva es cero. El campo dentro de la ranura debe contribuir con una parte que cancele el campo afuera. Por lo tanto, el campo que encontramos dentro de una ranura larga y delgada es igual al campo eléctrico promedio encontrado en el diélctrico.

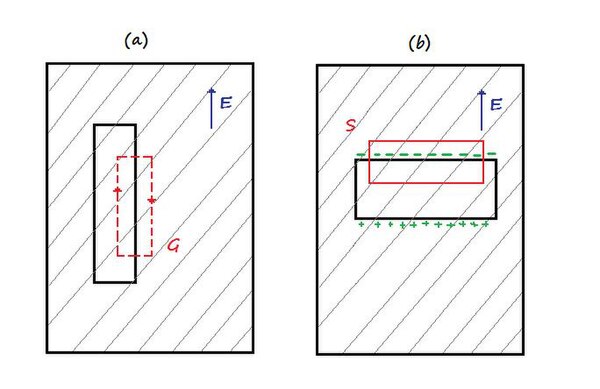
Ahora consideremos una ranura como se muestra en la parte (b), en este caso, el campo que encontramos enla renura no es el mismo que hay en el diélectrico debido a las cargas de polarización que aparecen en la superficie. Si usamos la ley de Gauss sobre la supreficie S que se muestra en la misma figura (b), encontramos que el campo electrico dentro de la ranura es

$E_{ranura}=E+{\frac {P}{\epsilon _{0}}}$

Donde E es el campo electrico dentro del dielectrico. Observese que la superficie gaussiana contiene la carga de polarizacion $\sigma _{pol}=P$

Ahora, ¿Cuál será el campo electrico dentro de un hoyo esférico? Imaginemo que recortamos una esfera de material dieléctrico y la sacamos de este, entonces, por el principio de superposición, podemos escribir el campo E promedio del dieléctrico como la suma del campo electrico dentro de la ranura esférica más el campo electrico del trozo esféreico de dielectrico que sacamos, denotaremos este ultimo por $E_{plug}$

$E=E_{hoyo}+E_{plug}$

El campo electrico dentro de la esfera es uniforme, y su valor es

$E_{plug}=-{\frac {P}{3\epsilon _{0}}}$

Y entonces

$E_{hoyo}=E+{\frac {P}{3\epsilon _{0}}}$

El campo dentro de una cavidad esférica es mayor que el promedio por una cantidad ${\frac {P}{3\epsilon _{0}}}$

Dielécticos Sólidos

El primer hecho interesante sobre los dieléctricos sólidos es que pueden estar permanentemente polarizados. Los materiales solidos de este tipo se llaman electrets. Un electret posee cargas de polarizacion permanentes en su superficie, es una especie de imán electrico, pero no es muy útil, porque cargas libres del aire son atraidas por eléctret y cancelan las cargas de polarización. En algunas sustancias critalinas podemos encontramos polarizacion interna permanente. Si cambiamos este momento dipolar, aparecen campo externos debido a que no hay tiempo de que las cargas se reordenen y se junten para cancelar las cargas de polarización. Por ejemplo, el momento puede ser cambiado calentando el dieléctrico, debido a la expansión termica. A este fenómeno se le conoce como piroelectricidad. Si el momento es cambiado mediante la aplicacion de tension sobre el material, encontramos pequeños efectos electricos, llamados piezoelectricidad.