Matemáticas/Geometría/Teorema de Tales
Teorema de Tales
[editar]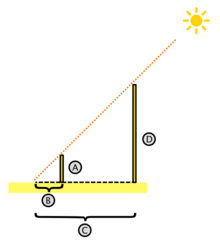
Se nombra así en nombre del geometro griego Tales de Mileto. El teorema de tales sirve para hacer dibujos a escala.
Primer teorema
[editar]Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:
"Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes." A el se debe una de las numerosas aplicaciones que tiene la semejanza, que es la determinación de la distancia entre dos puntos inaccesibles entre sí; para ello se dice que calcula la altura de una de las pirámides de Egipto sin medirla directamente, basándose en la longitud de la sombra de su bastón; así logró realizar una brillante triangulación.
Segundo teorema
[editar]
El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los [ángulos inscritos, consiste en el siguiente enunciado:
"Sea B un punto de la circunferencia de diámetro AC y centro "O", distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo donde <ABC = 90º"
