Matemáticas/Matemática Discreta/Texto completo

Matemática Discreta

La matemática discreta es un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables.

En oposición a las matemáticas continuas, que se encargan del estudio de conceptos como la continuidad y el cambio continuo, la matemáticas discretas estudian estructuras cuyos elementos pueden contarse uno por uno separadamente. Es decir, los procesos en matemáticas discretas son contables, como por ejemplo, los números enteros, grafos y sentencias de lógica.

Mientras que el cálculo infinitesimal está fundado en los números reales que no son numerables, la matemática discreta es la base de todo lo relacionado con los números naturales o conjuntos numerables. Son fundamentales para la ciencia de la computación, porque sólo son computables las funciones de conjuntos numerables.

• Definicion
• Proposicionalidad
• Predicados
• Teoría de Axiomas
• Definiciones
• Operaciones
• Axiomas

Definición

Se define cómo el residuo de una división no exacta donde

${\frac {a}{b}}=c+r$

Donde 'r es un número natural y se vuelve el módulo del número,mientras que es el divisor b y a el número modulado siempre y cuando sean números enteros:

$a,b\in \mathbb {Z}$ y $r\in \mathbb {N}$

Quedando expresado cómo:

$a{\pmod {b}}\equiv r$

Historia

En matemática, la aritmética modular es un sistema aritmético para clases de equivalencia de números enteros llamadas clases de congruencia. La aritmética modular fue introducida en 1801 por Carl Friedrich Gauss en su libro Disquisitiones Arithmeticae.

Algunas veces se le llama, sugerentemente, aritmética del reloj, ya que los números «dan la vuelta» tras alcanzar cierto valor llamado módulo.

Operaciones con Modulos

Suma y Resta

(+),Podemos definir las propiedades aritméticas para las sumas de congruencias:

Propiedad asociativa: a + (b + c) (mod (m)) = (a + b) + c (mod (m))

Elemento neutro: Existe un elemento 0 ∈ Zm, tal que a + 0 (mod (m)) = a (mod (m))

Elemento opuesto: Existe un elemento b ∈ Zm, tal que a + b = 0 (recordemos que 0 es el elemento neutro de la suma)

Propiedad conmutativa: a + b (mod (m)) = b + a (mod (m))

Propiedades principales

Clases de equivalencia módulo n

La aritmética modular se basa en una relación de equivalencia, y las clases de equivalencia de un entero a se denota con [a]_n (o simplemente [a] si sobreentendemos el módulo.) Otras notaciones son por ejemplo a + nZ o a mod n. El conjunto de todas las clases de equivalencia se denota con Z/nZ = { [0]_n, [1]_n, [2]_n,..., [n-1]_n }.

Esta relación de equivalencia tiene importantes propiedades que se siguen inmediatamente de la definición:

Si

$a_{1}\equiv b_{1}{\pmod {n}}$

y

$a_{2}\equiv b_{2}{\pmod {n}}$

entonces

$a_{1}+a_{2}\equiv b_{1}+b_{2}{\pmod {n}}$

y

$a_{1}a_{2}\equiv b_{1}b_{2}{\pmod {n}}$

Lo que muestra que la suma y la multiplicación son operaciones bien definidas sobre el conjunto de las clases de equivalencia. En otras palabras, la suma y la multiplicación están definidas sobre Z/nZ mediante las fórmulas siguientes:

$[a]_{n}+[b]_{n}=[a+b]_{n}\,\!$

$[a]_{n}\cdot [b]_{n}=[a\cdot b]_{n}$

De este modo, Z/nZ se convierte en un anillo con n elementos. Por ejemplo, en el anillo Z/12Z, se tiene :[8]₁₂[3]₁₂ + [6]₁₂ = [30]₁₂ = [6]₁₂.

El conjunto de enteros en Z/pZ forma un cuerpo finito si y sólo si p es primo.

Resolución de congruencias

Si a y b son enteros, la congruencia: ax ≡ b (mod n) tiene solución x si y sólo si el máximo común divisor (a, n) divide a b. Los detalles están recogidos en el teorema de congruencia lineal. Sistemas de congruencias más complicados con módulos diferentes se pueden resolver usando el teorema chino del resto o el método de sustitución sucesiva.

En el anillo de enteros, si consideramos la ecuación ax ≡ 1 (mod n), vemos que a tiene un inverso multiplicativo si y sólo si a y n son coprimos. Por tanto, Z/nZ es un cuerpo si y sólo si n es un primo. Se puede probar que cada cuerpo finito es una extensión de Z/pZ para algún primo p.

Pequeño teorema de Fermat y teorema de Euler

Un hecho importante sobre aritmética modular, cuando los módulos son números primos es el pequeño teorema de Fermat: si p es un número primo, entonces:

Si a es cualquier entero:

$a^{p}\equiv a{\pmod {p}}$

Si a es un entero no divisible entre p:

$a^{p-1}\equiv 1{\pmod {p}}$

Esto fue generalizado por Euler: para todo entero positivo n y todo entero a relativamente primo a n, :a^φ(n) ≡ 1 (mod n), donde φ(n) denota función phi de Euler que cuenta el número de enteros entre 1 y n que sean coprimos con respecto a n. El teorema de Euler es una consecuencia del teorema de Lagrange, aplicado al caso del grupo de las unidades del anillo Z/nZ.

Generalizaciones

Dos enteros a, b son congruentes módulo n, escrito como:a ≡ b (mod n) si su diferencia a − b es divisible entre n, esto es, si a − b = kn para algún entero k.

Usando esta definición, podemos generalizar a módulos no enteros. Por ejemplo, podemos definir a ≡ b (mod 2π) si a − b = k2π para algún entero k. Esta idea se desarrolla plenamente en el contexto de la teoría de los anillos y funciones trigonométricas.

En Álgebra abstracta se ve que la aritmética modular es un caso especial del proceso de crear un anillo factorial de un anillo módulo un ideal. Si R es un anillo conmutativo, e I es un ideal de R, entonces dos elementos a y b de R se dicen congruentes módulo I si a − b es un elemento de I. Como pasaba con el anillo de enteros, esto se convierte en una relación de equivalencia, y la suma y la multiplicación se convierten en operaciones bien definidas sobre el anillo factorial R/I.

Fuentes

http://gaussianos.com/teoria-de-numeros-elemental-aritmetica-modular/

https://es.wikipedia.org/wiki/Aritm%C3%A9tica_modular

https://es.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/what-is-modular-arithmetic

http://www.dma.fi.upm.es/recursos/aplicaciones/matematica_discreta/web/aritmetica_modular/

http://www.fiwiki.org/images/d/d3/MD_Tema3_AritmeticaModular.pdf

http://www.dma.fi.upm.es/recursos/aplicaciones/matematica_discreta/web/aritmetica_modular/congruencias.html La combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.

Combinaciones sin repetición

Dado un conjunto de n elementos distinguibles, se llama combinación sin repetición de p elementos, con p < n, elegidos entre los n, a cualquier subconjunto de p elementos distintos del conjunto.

El número de combinaciones sin repetición de p elementos elegidos entre los n se nota habitualmente

$C_{p}^{n}={\binom {n}{p}}={\frac {n!}{p!(n-p)!}}$ .

Ejemplo

Un estudiante debe responder a seis de las diez preguntas de las que consta un examen, ¿entre cuántos grupos de preguntas distintas puede elegir?

Se trata de determinar el número de grupos distintos de seis preguntas escogidas del conjunto de las diez, sabiendo que dos grupos con las mismas preguntas, aún en distinto orden, coinciden. En este caso, el número de grupos de preguntas distintos entre los que se puede elegir es

$C_{6}^{10}={\binom {10}{6}}={\frac {10!}{6!4!}}=210$

Combinaciones con repetición

Dado un conjunto de n elementos distinguibles, se llama combinación con repetición de p elementos escogidos entre los n a cualquier colección de p elementos del conjunto, con repeticiones eventuales de algunos de ellos.

El número de combinaciones con repetición de p elementos elegidos entre los n se nota habitualmente

$CR_{n}^{p}=C_{n+p-1}^{p}={\binom {n+p-1}{p}}={\frac {(n+p-1)!}{p!(n-1)!}}$

Ejemplo

¿De cuántas formas pueden elegirse simultáneamente tres bolas de una urna en la que hay al menos tres bolas blancas y tres negras indistinguibles?

Cada grupo es una disposicion no ordenada de tres colores formada por los colores blanco y negro con repeticion de alguno de ellos. Por tanto, se trata de determinar el número de grupos de tres elementos no ordenados. En este caso, el número de formas distintas de elegir simultáneamente tres bolas del conjunto es

$CR_{2}^{3}={\binom {4}{3}}={\frac {4!}{3!1!}}=4$

Fuente

Resumen adaptado de Wikipedia

La Teoría de grafos, también llamada Teoría de gráficas, es una rama de las matemáticas y las ciencias de la computación que estudia las propiedades de los grafos, y que no se debe confundir con las gráficas que tienen una acepción muy amplia. Formalmente, un grafo $G=(V,E)$ es una pareja ordenada en la que $V$ es un conjunto no vacío de vértices y $E$ es un conjunto de aristas. Donde $E$ consta de pares no ordenados de vértices, tales que si {${x,y}$}$\in E$ entonces decimos que $x$ e $y$ son adyacentes; y [en el grafo] se representa mediante una línea no orientada que una a dichos vértices. Si el grafo es dirigido se le llama digrafo, se denota $D$, y entonces el par $(x,y)$ es un par ordenado, y se representa con una flecha que va de $x$ a $y$, y decimos que $(x,y)\in A$.

La teoría de grafos tiene sus fundamentos en las matemáticas discretas y de las matemáticas aplicadas. Es una teoría que requiere de diferentes conceptos de diversas áreas como combinatoria, álgebra, probabilidad, geometría de polígonos, aritmética y topología. Actualmente ha tenido mayor preponderancia en el campo de la informática, las ciencias de la computación y telecomunicaciones. Debido a la gran cantidad de aplicaciones en la optimización de recorridos, procesos, flujos, algoritmos de búsquedas, entre otros, se generó toda una nueva teoría que se conoce como análisis de redes.

Historia

Los 7 puentes del río Pregel en Königsberg.

El origen de la teoría de grafos se remonta al siglo XVIII con el problema de los puentes de Königsberg, el cual consistía en encontrar un camino que recorriera los siete puentes del río Pregel (Plantilla:Coord) en la ciudad de Königsberg, actualmente Kaliningrado, de modo que se recorrieran todos los puentes pasando una sola vez por cada uno de ellos. El trabajo de Leonhard Euler sobre el problema titulado Solutio problematis ad geometriam situs pertinentis (La solución de un problema relativo a la geometría de la posición) en 1736, es considerado el primer resultado de la teoría de grafos. También se considera uno de los primeros resultados topológicos en geometría (que no depende de ninguna medida). Este ejemplo ilustra la profunda relación entre la teoría de grafos y la topología.

Luego, en 1847, Gustav Kirchhoff utilizó la teoría de grafos para el análisis de redes eléctricas publicando sus leyes de los circuitos para calcular el voltaje y la corriente en los circuitos eléctricos, conocidas como leyes de Kirchhoff, considerado la primera aplicación de la teoría de grafos a un problema de ingeniería.

En 1852 Francis Guthrie planteó el problema de los cuatro colores el cual afirma que es posible, utilizando solamente cuatro colores, colorear cualquier mapa de países de tal forma que dos países vecinos nunca tengan el mismo color. Este problema, que no fue resuelto hasta un siglo después por Kenneth Appel y Wolfgang Haken en 1976, puede ser considerado como el nacimiento de la teoría de grafos. Al tratar de resolverlo, los matemáticos definieron términos y conceptos teóricos fundamentales de los grafos.

En 1857, Arthur Cayley estudió y resolvió el problema de enumeración de los isómeros, compuestos químicos con idéntica composición (fórmula) pero diferente estructura molecular. Para ello representó cada compuesto, en este caso hidrocarburos saturados C_nH_2n+2, mediante un grafo árbol donde los vértices representan átomos y las aristas la existencia de enlaces químicos.

El término «grafo», proviene de la expresión H«graphic notation» usada por primera vez por Edward Frankland y posteriormente adoptada por Alexander Crum Brown en 1884, y hacía referencia a la representación gráfica de los enlaces entre los átomos de una molécula.

El primer libro sobre teoría de grafos fue escrito por Dénes Kőnig y publicado en 1936.

Aplicaciones

Gracias a la teoría de grafos se pueden resolver diversos problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o sistemas de apertura. Se utiliza para diferentes áreas por ejemplo, Dibujo computacional, en toda las áreas de Ingeniería.

Los grafos se utilizan también para modelar trayectos como el de una línea de autobús a través de las calles de una ciudad, en el que podemos obtener caminos óptimos para el trayecto aplicando diversos algoritmos como puede ser el algoritmo de Floyd.

Para la administración de proyectos, utilizamos técnicas como técnica de revisión y evaluación de programas (PERT) en las que se modelan los mismos utilizando grafos y optimizando los tiempos para concretar los mismos.

La teoría de grafos también ha servido de inspiración para las ciencias sociales, en especial para desarrollar un concepto no metafórico de red social que sustituye los nodos por los actores sociales y verifica la posición, centralidad e importancia de cada actor dentro de la red. Esta medida permite cuantificar y abstraer relaciones complejas, de manera que la estructura social puede representarse gráficamente. Por ejemplo, una red social puede representar la estructura de poder dentro de una sociedad al identificar los vínculos (aristas), su dirección e intensidad y da idea de la manera en que el poder se transmite y a quiénes.

Se emplea en problemas de control de producción, para proyectar redes de ordenadores, para diseñar módulos electrónicos modernos y proyectar sistemas físicos con parámetros localizados (mecánicos, acústicos y eléctricos).

Se usa para la solución de problemas de genética y problemas de automatización de la proyección (SAPR). Apoyo matemático de los sistemas modernos para el procesamiento de la información. Acude en las investigaciones nucleares (técnica de diagramas de Feynman).

Los grafos son importantes en el estudio de la biología y hábitat. El vértice representa un hábitat y las aristas (o "edges" en inglés) representa los senderos de los animales o las migraciones. Con esta información, los científicos pueden entender cómo esto puede cambiar o afectar a las especies en su hábitat.

• 
  Mapas conceptuales
• 
  Plano de estaciones del metro.
• 
  Plano de autopistas.
• 
  Circuito eléctrico
• 
  Sociograma de una red social
• 
  Topología de red de computadores
• 
  Organigramas
• 
  Isomeros
• 
  Arquitectura de redes de telefonía móvil
• 
  Draws de eliminación directa (ej: tenis)

Entre las aplicaciones de la Teoría de gráficas que se han vuelto importantes en la actualidad podemos encontrar el estudio de las redes sociales, cuya importancia radica en el adecuado almacenamiento de datos, puesto que el costo del tiempo de búsqueda de la información de cada miembro que pertenece a esta red puede tornarse demasiado alto debido al número de usuarios. Por ejemplo, el número de usuarios que hay actualmente en una importante red social tan solo en México es de 49 millones -cifra reportada por el periódico El economista en 2014-, si este número lo multiplicamos por 194 que es el número aproximado de países que hay en el mundo, se percibe la posibilidad de un grave problema de almacenamiento para los servidores que hay destinados para ello y para la búsqueda de información. Este mismo fenómeno pasa en otras redes de fotografías, mensajes, etc. El modelado de este tipo de problemas ha sido abordado principalmente por estudiantes de doctorado de universidades como Stanford, Massachusetts Institute of Technology (MIT), Berkeley, Oxford, Rice y también por la NASA; en México, tanto el Instituto Politécnico Nacional (IPN) como la Universidad Nacional Autónoma de México (UNAM) son los principales promotores en estas áreas a través de los grupos académicos de combinatoria y de computación científica. Podemos considerar que este tipo de problemas son tratados por expertos en matemáticas y ciencias de la computación, debido a su alto grado de complejidad.

El cerebro humano es una red compleja que  interactúa en regiones conectadas por tractos de sustancia blanca. La caracterización de características estructurales y funcionales de una red tal en sujetos sanos y personas enfermas tiene la posibilidad de mejorar nuestra comprensión de la fisiopatología y las manifestaciones neurológicas y condiciones psiquiátricas. Esto ha llevado al uso de nuevas herramientas para el análisis de sistemas complejos para hacer frente enfermedades cerebrales. Entre estos, la teoría de grafos es un marco matemático que permite describir una red en forma de una  gráfica, que consiste en una colección de los nodos (es decir, regiones del cerebro) y los bordes (es decir, estructurales y conexiones funcionales) .El uso de la teoría de grafos, distinto modificaciones de la topología de red cerebro han sido identificados durante el desarrollo y el envejecimiento normal, y se rompieron conectividades funcionales y estructurales han sido asociado con varios trastornos neurológicos y psiquiátricos, incluyendo demencia, esclerosis lateral amiotrófica, y la esquizofrenia. En este último enfoque se ha contribuido a probar la teoría de esta condición como un síndrome de desconexión. En la esclerosis múltiple (MS), la ocurrencia de la desconexión ha sido corroborada por estudios de resonancia magnética estructural de topología de la red cerebral que mostró una disminución de la conectividad estructural de las regiones de los lóbulos fronto-temporal.

Otra aplicación de las gráficas consiste en tomar datos de resonancia magnética del cerebro adquiridos en condición ausente ( estado de reposo ) requieren nuevos análisis de datos técnicas que no dependen de un modelo de activación, una alternativa son los métodos libre de parámetro en base a una forma particular de la centralidad del vector propio asociado a un nodo llamado de centralidad; la centralidad del vector propio asigna atributos de un valor a cada voxel en el cerebro de manera que un voxel recibe un valor grande si está fuertemente correlacionada con muchos otros nodos que son centrales dentro de la red; el algoritmo PageRank de Google es una variante del vector propio centralidad el cual es utilizado en las búsquedas que se efectúan en internet. Hasta el momento, otras medidas de centralidad - en particular centralidad de intermediación - se han aplicado a datos de la fMRI usando un conjunto pre-seleccionado de nodos que consisten en varios cientos de elementos. Centralidad del Vector Propio es computacionalmente mucho más eficiente que centralidad de intermediación y no requiere de umbrales de valores de similitud de modo que se puede aplicar a miles de voxels en una región de interés que cubren la totalidad del cerebro que habría sido inviable el uso de centralidad de intermediación. Centralidad del Vector Propio se puede utilizar en una variedad de diferentes medidas de similitud. (Lohmann et al., 2010). “La teoría de redes complejas juega un papel importante en una amplia variedad de disciplinas, que van desde la informática, sociología, ingeniería y física, para molecular y la biología de la población. Dentro de los campos de la biología y la medicina, el potencial de aplicaciones de análisis de redes incluyen, por ejemplo, la identificación objetivo de drogas, determinando una función del gen de la proteína, o diseñar estrategias eficaces para el tratamiento de diversas enfermedades o proporcionar el diagnóstico precoz de trastornos. “ (Pavlopoulos et al., 2011) La teoría de gráficas, es adecuada para que los informáticos modelen problemas, pero también es adecuado para los matemáticos que tienen interés en la complejidad computacional. La mayoría de los conceptos clásicos de la teoría de grafos teórica y aplicada (árboles de expansión, conectividad, género, colorabilidad, fluye en las redes, los apareamientos y recorridos). Se usa en la solución de problemas.(Czumaj, Jansen, Meyer auf der Heide, & Schiermeyer, 2006)

Tipos de grafos

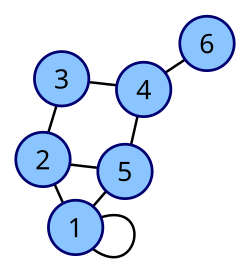
• Grafo simple. o simplemente grafo es aquel que acepta una sola arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un grafo.
• Multigrafo. Es el que acepta más de una arista entre dos vértices. Estas aristas se llaman múltiples o lazos (loops en inglés). Los grafos simples son una subclase de esta categoría de grafos. También se les llama grafos general.
• Pseudografo. Si incluye algún lazo.
• Grafo orientado, dirigido o digrafo. Son grafos en los cuales se ha añadido una orientación a las aristas, representada gráficamente por una flecha.
• Grafo etiquetado. Grafos en los cuales se ha añadido un peso a las aristas (número entero generalmente) o un etiquetado a los vértices.
• Grafo aleatorio. Grafo cuyas aristas están asociadas a una probabilidad.
• Hipergrafo. Grafos en los cuales las aristas tienen más de dos extremos, es decir, las aristas son incidentes a 3 o más vértices.
• Grafo infinito. Grafos con conjunto de vértices y aristas de cardinal infinito.

Representación de grafos

El artículo principal de esta categoría es Grafo (estructura de datos).

Existen diferentes formas de representar un grafo (simple), además de la geométrica y muchos métodos para almacenarlos en una computadora. La estructura de datos usada depende de las características del grafo y el algoritmo usado para manipularlo. Entre las estructuras más sencillas y usadas se encuentran las listas y las matrices, aunque frecuentemente se usa una combinación de ambas. Las listas son preferidas en grafos dispersos porque tienen un eficiente uso de la memoria. Por otro lado, las matrices proveen acceso rápido, pero pueden consumir grandes cantidades de memoria.

Estructura de lista

• Lista de incidencia - Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.

• Lista de adyacencia - Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.

• Lista de grados - También llamada secuencia de grados o sucesión gráfica de un grafo no-dirigido es una secuencia de números, que corresponde a los grados de los vértices del grafo.

Estructuras matriciales

• Matriz de adyacencia - El grafo está representado por una matriz cuadrada M de tamaño $n^{2}$, donde $n$ es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento $m_{x,y}$ es 1, de lo contrario, es 0.

• Matriz de incidencia - El grafo está representado por una matriz de A (aristas) por V (vértices), donde [vértice, arista] contiene la información de la arista (1 - conectado, 0 - no conectado)

Grafo G(V,A)	Conjuntos	Matriz de adyacencia	Matriz de incidencia	Secuencia de grados	Lista de Adyacencia
	V = { 1, 2, 3, 4, 5, 6 } A = { {1,1}, {1,2}, {1,5}, {2,3}, {2,5}, {3,4}, {4,5}, {4,6} }	${\begin{pmatrix}1&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{pmatrix}}$	${\begin{pmatrix}1&1&1&0&0&0&0&0\\0&1&0&1&1&0&0&0\\0&0&0&1&0&1&0&0\\0&0&0&0&0&1&1&1\\0&0&1&0&1&0&1&0\\0&0&0&0&0&0&0&1\\\end{pmatrix}}$	(4,3,3,3,2,1)	{ {1,2,5}, {3,5}, {4}, {5,6} }

Problemas de teoría de grafos

Ciclos y caminos hamiltonianos

El artículo principal de esta categoría es Ciclo hamiltoniano.

Ejemplo de un ciclo Hamiltoniano.

Un ciclo es una sucesión de aristas adyacentes, donde no se recorre dos veces la misma arista, y donde se regresa al punto inicial. Un ciclo hamiltoniano tiene además que recorrer todos los vértices exactamente una vez (excepto el vértice del que parte y al cual llega).

Por ejemplo, en un museo grande (al estilo del Louvre), lo idóneo sería recorrer todas las salas una sola vez, esto es buscar un ciclo hamiltoniano en el grafo que representa el museo (los vértices son las salas, y las aristas los corredores o puertas entre ellas).

Se habla también de Camino hamiltoniano si no se impone regresar al punto de partida, como en un museo con una única puerta de entrada. Por ejemplo, un caballo puede recorrer todas las casillas de un tablero de ajedrez sin pasar dos veces por la misma: es un camino hamiltoniano. Ejemplo de un ciclo hamiltoniano en el grafo del dodecaedro.

Hoy en día, no se conocen métodos generales para hallar un ciclo hamiltoniano en tiempo polinómico, siendo la búsqueda por fuerza bruta de todos los posibles caminos u otros métodos excesivamente costosos. Existen, sin embargo, métodos para descartar la existencia de ciclos o caminos hamiltonianos en grafos pequeños.

El problema de determinar la existencia de ciclos hamiltonianos, entra en el conjunto de los NP-completos.

Un grafo es plano si se puede dibujar sin cruces de aristas. El problema de las tres casas y los tres pozos tiene solución sobre el toro, pero no en el plano.

Grafos planos

El artículo principal de esta categoría es Grafo plano.

Cuando un grafo o multigrafo se puede dibujar en un plano sin que dos segmentos se corten, se dice que es plano.

Un juego muy conocido es el siguiente: Se dibujan tres casas y tres pozos. Todos los vecinos de las casas tienen el derecho de utilizar los tres pozos. Como no se llevan bien en absoluto, no quieren cruzarse jamás. ¿Es posible trazar los nueve caminos que juntan las tres casas con los tres pozos sin que haya cruces?

Cualquier disposición de las casas, los pozos y los caminos implica la presencia de al menos un cruce.

Sea K_n el grafo completo con n vértices, K_{n, p} es el grafo bipartito de n y p vértices.

El juego anterior equivale a descubrir si el grafo bipartito completo K_3,3 es plano, es decir, si se puede dibujar en un plano sin que haya cruces, siendo la respuesta que no. En general, puede determinarse que un grafo no es plano, si en su diseño puede encontrase una estructura análoga (conocida como menor) a K₅ o a K_3,3.

Establecer qué grafos son planos no es obvio, y es un problema que tiene que ver con topología.

Coloración de grafos

El artículo principal de esta categoría es Coloración de grafos.

Si G=(V, E) es un grafo no dirigido, una coloración propia de G, ocurre cuando coloreamos los vértices de G de modo que si {a, b} es una arista en G entonces a y b tienen diferentes colores. (Por lo tanto, los vértices adyacentes tienen colores diferentes). El número mínimo de colores necesarios para una coloración propia de G es el número cromático de G y se escribe como C (G). Sea G un grafo no dirigido sea λ el número de colores disponibles para la coloración propia de los vértices de G. Nuestro objetivo es encontrar una función polinomial P (G,λ), en la variable λ, llamada polinomio cromático de G, que nos indique el número de coloraciones propias diferentes de los vértices de G, usando un máximo de λ colores.

Descomposición de polinomios cromáticos. Si G=(V, E) es un grafo conexo y e pertenece a Ε, entonces: P (G,λ)=P (G+e,λ)+P (G/e,λ), donde G/e es el grafo se obtiene por contracción de aristas.

Para cualquier grafo G, el término constante en P (G,λ) es 0

Sea G=(V, E) con |E|>0 entonces, la suma de los coeficientes de P (G,λ) es 0.

Sea G=(V, E), con a, b pertenecientes al conjunto de vértices V pero {a, b}=e, no perteneciente a al conjunto de aristas E. Escribimos G+e para el grafo que se obtiene de G al añadir la arista e={a, b}. Al identificar los vértices a y b en G, obtenemos el subgrafo G++e de G.0000

Teorema de los cuatro colores

El artículo principal de esta categoría es Teorema de los cuatro colores.

Plantilla:Imagen múltiple Otro problema famoso relativo a los grafos: ¿Cuántos colores son necesarios para dibujar un mapa político, con la condición obvia que dos países adyacentes no puedan tener el mismo color? Se supone que los países son de un solo pedazo, y que el mundo es esférico o plano. En un mundo en forma de toroide; el teorema siguiente no es válido:

Cuatro colores son siempre suficientes para colorear un mapa.

El mapa siguiente muestra que tres colores no bastan: Si se empieza por el país central a y se esfuerza uno en utilizar el menor número de colores, entonces en la corona alrededor de a alternan dos colores. Llegando al país h se tiene que introducir un cuarto color. Lo mismo sucede en i si se emplea el mismo método.

La forma precisa de cada país no importa; lo único relevante es saber qué país toca a qué otro. Estos datos están incluidos en el grafo donde los vértices son los países y las aristas conectan los que justamente son adyacentes. Entonces la cuestión equivale a atribuir a cada vértice un color distinto del de sus vecinos.

Hemos visto que tres colores no son suficientes, y demostrar que con cinco siempre se llega, es bastante fácil. Pero el teorema de los cuatro colores no es nada obvio. Prueba de ello es que se han tenido que emplear ordenadores para acabar la demostración (se ha hecho un programa que permitió verificar una multitud de casos, lo que ahorró muchísimo tiempo a los matemáticos). Fue la primera vez que la comunidad matemática aceptó una demostración asistida por ordenador, lo que creó en su día una cierta polémica dentro de dicha comunidad.

Caracterización de grafos

Grafos simples

Un grafo es simple si a lo sumo existe una arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos.

Un grafo que no es simple se denomina multigrafo.

Grafos conexos

Un grafo es conexo si cada par de vértices está conectado por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde a hacia b.

Un grafo es doblemente conexo si cada par de vértices está conectado por al menos dos caminos disjuntos; es decir, es conexo y no existe un vértice tal que al sacarlo el grafo resultante sea disconexo.

Es posible determinar si un grafo es conexo usando un algoritmo Búsqueda en anchura (BFS) o Búsqueda en profundidad (DFS).

En términos matemáticos la propiedad de un grafo (fuertemente) conexo permite establecer una relación de equivalencia para sus vértices, la cual lleva a una partición de estos en "componentes (fuertemente) conexos", es decir, porciones del grafo, que son (fuertemente) conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

Grafo conexo y no conexo

Grafos completos

El artículo principal de esta categoría es Grafo completo.

Un grafo es completo si existen aristas uniendo todos los pares posibles de vértices. Es decir, todo par de vértices (a, b) debe tener una arista e que los une.

El conjunto de los grafos completos es denominado usualmente $\mathbb {K}$, siendo $\mathbb {K} _{n}$ el grafo completo de n vértices.

Un $\mathbb {K} _{n}$, es decir, grafo completo de $n$ vértices tiene exactamente ${\frac {n(n-1)}{2}}$ aristas.

La representación gráfica de los $\mathbb {K} _{n}$ como los vértices de un polígono regular da cuenta de su peculiar estructura.

Grafos bipartitos

El artículo principal de esta categoría es Grafo bipartito.

Un grafo G es bipartito si puede expresar como $G=\{V_{1}\cup V_{2},A\}$ (es decir, sus vértices son la unión de dos grupos de vértices), bajo las siguientes condiciones:

• $V_{1}$ y $V_{2}$ son disjuntos y no vacíos.
• Cada arista de A une un vértice de V₁ con uno de V₂.
• No existen aristas uniendo dos elementos de V₁; análogamente para V₂.

Bajo estas condiciones, el grafo se considera bipartito, y puede describirse informalmente como el grafo que une o relaciona dos conjuntos de elementos diferentes, como aquellos resultantes de los ejercicios y puzzles en los que debe unirse un elemento de la columna A con un elemento de la columna B.

Homeomorfismo de grafos

El artículo principal de esta categoría es Homeomorfismo de grafos.

Dos grafos $G_{1}$ y $G_{2}$ son homeomorfos si ambos pueden obtenerse a partir del mismo grafo con una sucesión de subdivisiones elementales de aristas.

Árboles

El artículo principal de esta categoría es Árbol (teoría de grafos).

Ejemplo de árbol.

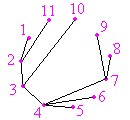
Un grafo que no tiene ciclos y que conecta a todos los puntos, se llama un árbol. En un grafo con n vértices, los árboles tienen exactamente n - 1 aristas, y hay n^n-2 árboles posibles. Su importancia radica en que los árboles son grafos que conectan todos los vértices utilizando el menor número posible de aristas. Un importante campo de aplicación de su estudio se encuentra en el análisis filogenético, el de la filiación de entidades que derivan unas de otras en un proceso evolutivo, que se aplica sobre todo a la averiguación del parentesco entre especies; aunque se ha usado también, por ejemplo, en el estudio del parentesco entre lenguas.

Grafos ponderados o etiquetados

En muchos casos, es preciso atribuir a cada arista un número específico, llamado valuación, ponderación o coste según el contexto, y se obtiene así un grafo valuado.
Formalmente, es un grafo con una función v: A → R₊.

Por ejemplo, un representante comercial tiene que visitar n ciudades conectadas entre sí por carreteras; su interés previsible será minimizar la distancia recorrida (o el tiempo, si se pueden prever atascos). El grafo correspondiente tendrá como vértices las ciudades, como aristas las carreteras y la valuación será la distancia entre ellas.
Y, de momento, no se conocen métodos generales para hallar un ciclo de valuación mínima, pero sí para los caminos desde a hasta b, sin más condición.

Diámetro

En la figura se nota que K₄ es plano (desviando la arista ab al exterior del cuadrado), que K₅ no lo es, y que K₃,₂ lo es también (desvíos en gris).

En un grafo, la distancia entre dos vértices es el menor número de aristas de un recorrido entre ellos. El diámetro, en una figura como en un grafo, es la mayor distancia de entre todos los pares de puntos de la misma.

El diámetro de los K_n es 1, y el de los K_n,_p es 2. Un diámetro infinito puede significar que el grafo tiene una infinidad de vértices o simplemente que no es conexo. También se puede considerar el diámetro promedio, como el promedio de las distancias entre dos vértices.

El mundo de Internet ha puesto de moda esa idea del diámetro: Si descartamos los sitios que no tienen enlaces, y escogemos dos páginas web al azar: ¿En cuántos clics se puede pasar de la primera a la segunda? El resultado es el diámetro de la Red, vista como un grafo cuyos vértices son los sitios, y cuyas aristas son lógicamente los enlaces.

En el mundo real hay una analogía: tomando al azar dos seres humanos del mundo, ¿En cuántos saltos se puede pasar de uno a otro, con la condición de sólo saltar de una persona a otra cuando ellas se conocen personalmente? Con esta definición, se estima que el diámetro de la humanidad es de... ¡ocho solamente!

Este concepto refleja mejor la complejidad de una red que el número de sus elementos.

Véase también: Glosario en teoría de grafos

Algoritmos importantes

• Algoritmo de búsqueda en anchura (BFS)
• Algoritmo de búsqueda en profundidad (DFS)
• Algoritmo de búsqueda A*
• Algoritmo del vecino más cercano
• Ordenación topológica de un grafo
• Algoritmo de cálculo de los componentes fuertemente conexos de un grafo
• Algoritmo de Dijkstra
• Algoritmo de Bellman-Ford
• Algoritmo de Prim
• Algoritmo de Ford-Fulkerson
• Algoritmo de Kruskal
• Algoritmo de Floyd-Warshall

Investigadores relevantes en Teoría de grafos

• Alon, Noga
• Berge, Claude
• Bollobás, Béla
• Brightwell, Graham
• Chung, Fan
• Dirac, Gabriel Andrew
• Dijkstra, Edsger
• Edmonds, Jack
• Erdős, Paul
• Euler, Leonhard
• Faudree, Ralph
• Golumbic, Martin
• Graham, Ronald
• Harary, Frank
• Heawood, Percy John
• Kaufmann, Walter Arnold
• Kőnig, Dénes
• Kuratowski, Kazimierz
• Lovász, László
• Nešetřil, Jaroslav
• Rényi, Alfréd
• Ringel, Gerhard
• Robertson, Neil
• Seymour, Paul
• Szemerédi, Endre
• Thomas, Robin
• Thomassen, Carsten
• Turán, Pál
• Tutte, W. T.
• Whitney, Hassler

Véase también

• Grafo
• Anexo:Galería de grafos
• Teorema de König (teoría de grafos)

Referencias

Czumaj, A., Jansen, K., Meyer auf der Heide, F., & Schiermeyer, I. (2006). Algorithmic Graph Theory. Oberwolfach Reports, 379–460.

Hinz, A. M. (2012). Graph theory of tower tasks. In Behavioural Neurology (Vol. 25, pp. 13–22).

Lohmann, G., Margulies, D. S., Horstmann, A., Pleger, B., Lepsien, J., Goldhahn, D., … Turner, R. (2010). Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain. PLoS ONE, 5(4). http://doi.org/10.1371/journal.pone.0010232

Pavlopoulos, G. a, Secrier, M., Moschopoulos, C. N., Soldatos, T. G., Kossida, S., Aerts, J., … Bagos, P. G. (2011). Using graph theory to analyze biological networks. BioData Mining, 4(1), 10. Retrieved from http://www.biodatamining.org/content/4/1/10

Rocca, M. A., Valsasina, P., Meani, A., Falini, A., Comi, G., & Filippi, M. (2014). Impaired functional integration in multiple sclerosis: a graph theory study. Brain Structure and Function, 115–131. http://doi.org/10.1007/s00429-014-0896-4

Enlaces externos

Commons

• Wikimedia Commons alberga contenido multimedia sobre Matemáticas/Matemática Discreta/Texto completo.
• Sobre los grafos VPT y los grafos EPT. Mazzoleni, María Pía. 30 de mayo de 2014.

En Matemáticas, una relación de recurrencia es una ecuación que define una secuencia recursiva; cada término de la secuencia es definido como una función de términos anteriores.

Definición

Una ecuación recurrente es un tipo específico de relación de recurrencia. Una relación de recurrencia para la sucesión $a_{0},a_{1},a_{2},\ldots$ es una ecuación que relaciona $a_{n}\,$ con alguno de sus predecesores $a_{0},a_{1},\ldots ,a_{n-1}$. Las condiciones iniciales para la sucesión $a_{0},a_{1},\ldots$ son valores dados en forma explícita para un número finito de términos de la sucesión.

Resolver una relación de recurrencia consiste en determinar una fórmula explícita (cerrada) para el término general $a_{n}\,$, es decir una función no recursiva de n.

Hay tres métodos para resolver relaciones recurrentes: iteración, transformada Z y un método especial que se aplica a las relaciones de recurrencia lineales homogéneas con coeficientes constantes.

Un ejemplo de una relación de recurrencia es el siguiente:

$x_{n+1}=rx_{n}(1-x_{n})\,$

Algunas definiciones de recurrencia pueden tener relaciones muy complejas (caóticas), y sus comportamientos a veces son estudiados por los físicos y matemáticos en un campo conocido como análisis no lineal.

Resolución

Por hipótesis comprobada

La forma más sencilla para resolver una relación de recurrencia es formular una posible solución (hipótesis) y comprobar por inducción la validez de la misma.

En el caso de las "Torres de Hanoi", siendo $t$ el número de pasos para resolver el problema con $n$ discos, $t_{n}$ está dado por la siguiente ecuación de recurrencia:

$t_{1}:=1;\,t_{n}:=2t_{n-1}+1$

Resolver la recurrencia sería encontrar la ecuación que nos da el valor de $t_{n}$ en términos de $n$.

Al analizar la correspondencia para cada valor de $t_{n}$ con n desde $\{1,2,3,4,5\}\rightarrow \{1,3,7,15,31\}$ especulamos que quizás la solución sea $t_{n}:=2^{n}-1$, por lo que para comprobarla se procede a sustituir la hipótesis en la ecuación de recurrencia:

$t_{n}=2t_{n-1}+1=2(2^{n-1}-1)+1=2({\frac {2^{n}}{2}}-1)+1=(2^{n}-2)+1=2^{n}-1$

comprobándose la hipótesis como verdadera.

Iteración

Para resolver una relación de recurrencia asociada a la sucesión: $a_{0},a_{1},a_{2}\,$ por iteración, utilizamos la relación de recurrencia para escribir el n-ésimo término $a_{n}\,$ en términos de algunos de sus predecesores. Luego utilizamos de manera sucesiva la relación de recurrencia para reemplazar cada uno de los términos por algunos de sus predecesores. Continuamos hasta llegar a alguno de los casos base.

Recurrencias Lineales

Una relación de recurrencia es lineal de grado k si tiene la siguiente estructura:

$c_{0}(n)a_{n}+c_{1}(n)a_{n-1}+...+c_{k-1}(n)a_{n-k+1}+c_{k}(n)a_{n-k}\,=0$

siendo $c_{i}(n)\,$ funciones reales de $n\,$, y $F(n)\,$ una función de n.

El adjetivo lineal indica que cada término de la secuencia está definido como una función lineal de sus términos anteriores. El orden de una relación de recurrencia lineal es el número de términos anteriores exigidos por la definición.

En la relación $a_{n}=a_{n-2}\,$ el orden es dos, porque debe haber al menos dos términos anteriores (ya sean usados o no).

Ejemplos :

$3a_{n}-{n-1}a_{n-1}+2a_{n-2}=0\,$

Ecuación de Recurrencia lineal homogénea con coeficientes constantes

Se llama ecuación de recurrencia lineal homogénea de grado k, con coeficientes constantes, a una expresión del tipo:

$a_{n}+c_{1}a_{n-1}+c_{2}a_{n-2}+\cdots +c_{k}a_{n-k}=0,c_{i}\in \mathbf {R} ,c_{k}\neq 0$

Para poder encontrar una solución, hacen falta unas condiciones de contorno o iniciales $a_{0},a_{1},\cdots ,a_{k-1}$, siendo k el grado de la ecuación.

La recurrencia lineal, junto con las condiciones iniciales $a_{0},\cdots ,a_{k-1}$, determinan la secuencia única.

Sea la ecuación de recurrencia lineal homogénea de orden k anterior, se denomina ecuación característica a la ecuación de grado k:

$x^{k}+c_{1}x^{k-1}+\cdots +c_{k}$

La generación de la función racional

Las secuencias lineales recursiva son precisamente las secuencias cuya función de generación es una función racional: el denominador es el polinomio auxiliar (a una transformación), y el numerador se obtiene con los valores iniciales.

El caso más sencillo son las secuencias periódicas,$a_{n}=a_{n-d}$, n≥d que tienen secuencia $a_{0},a_{1},\cdots ,a_{d-1},a_{0},\cdots$ y función de generación una suma de una serie geométrica:

${\begin{array}{ll}{\cfrac {a_{0}+a_{1}x^{1}+\dots +a_{d-1}x^{d-1}}{1-x^{d}}}=&(a_{0}+a_{1}x^{1}+\dots +a_{d-1}x^{d-1})+\\&(a_{0}+a_{1}x^{1}+\dots +a_{d-1}x^{d-1})x^{d}+\\&(a_{0}+a_{1}x^{1}+\dots +a_{d-1}x^{d-1})x^{2d}+\\&\dots \end{array}}$

Más general, dada la relación de recurrencia:

$a_{n}=c_{1}a_{n-1}+c_{2}a_{n-2}+...+c_{d}a_{n-d}\,$

con función de generación

$a_{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots$

la serie es aniquilada por $a_{k}$ y anteriormente por el polinomio:

$1-c_{1}x^{1}-c_{2}x^{2}-\cdots -c_{d}x^{d}$

Eso es, multiplicando la función de generación por el polinomio

$b_{n}=a_{n}-c_{1}a_{n-1}-c_{2}a_{n-2}-\cdots -c_{d}a_{n-d}$

como el coeficiente en $x^{n}$, que desaparece (por la relación de recurrencia) para n ≥ d. Así:

$(a_{0}+a_{1}x^{1}+a_{2}x^{2}+\dots )(1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d})=(b_{0}+b_{1}x^{1}+b_{2}x^{2}+\dots +b_{d-1}x^{d-1})$

como dividiendo:

$a_{0}+a_{1}x^{1}+a_{2}x^{2}+\dots ={\cfrac {b_{0}+b_{1}x^{1}+b_{2}x^{2}+\dots +b_{d-1}x^{d-1}}{1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}}}$

expresando la función de generación como una función racional. El denominador es $x^{d}p(1/x)$, una transformación del polinomio auxiliar (equivalente, invirtiendo el orden de los coeficientes); también se puede usar cualquier múltiplo de esta, pero esta normalización es elegida por ambas porque la relación simple del polinomio auxiliar, y de ese modo $b_{0}=a_{0}$.

Relación con la diferencia de ecuaciones

Dada una secuencia $\{a_{n}\}\,$ de números reales: la primera diferencia $d(a_{n})\,$ se define como $a_{n}-a_{n-1}\,$

La segunda diferencia $d^{2}(a_{n})\,$ se define como $d(a_{n})-d(a_{n-1})\,$,

que se puede simplificar a $a_{n}-2a_{n-1}+a_{n-2}\,$.

Más general: la diferencia $d^{k}\,$ se define como $d^{k-1}(a_{n})-d^{k-1}(a_{n-1})\,$

A diferencia de la ecuación es una ecuación compuesta por $a_{n}$ y sus diferencias. Cada relación de recurrencia puede ser formulada como una ecuación de diferencia. Por el contrario, cada ecuación de diferencia puede ser formulada como una relación de recurrencia. Algunos autores así utilizan los dos términos intercambiables. Por ejemplo, la ecuación de la diferencia:

$3d^{2}(a_{n})+2d(a_{n})+7a_{n}=0\,$

es equivalente a la relación de recurrencia:

$12a_{n}=8a_{n-1}-3a_{n-2}\,$

De este modo se puede resolver relaciones de recurrencia por la reiteración como ecuaciones diferencia, y luego la solución de la ecuación de diferencia, análogamente como una solución de ecuaciones diferenciales ordinarias.

Ver escala de tiempo de cálculo para la unificación de la teoría de las ecuaciones de diferencia con la de las ecuaciones diferenciales.

Resolución

Sean

$c_{0}a_{n}+c_{1}a_{n-1}+c_{2}a_{n-2}+\cdots +c_{k}a_{n-k}=0$

una ecuación de recurrencia lineal homogénea, $x^{k}+c_{n-1}x^{k-1}+\cdots +c_{n-k}$ su ecuación característica y, $x_{1},x_{2},\cdots ,x_{s}$ las raíces de la ecuación característica con multiplicidades $m_{1},m_{2},\cdots ,m_{s}$ respectivamente. La solución de esta ecuación sería:

Definición. $a_{n}=P_{1}(n)(x_{1})^{n}+P_{2}(n)(x_{2})^{n}+\cdots +P_{s}(n)(x_{s})^{n}$

Con $P_{i}(n)\$ el polinomio de grado menor o igual que $m_{i}-1\,$. Para poder calcular los coeficientes de los polinomios $P_{i}(n)\,$, necesitamos saber las condiciones iniciales de la ecuación de recurrencia.

Ejemplo : Números de Fibonacci

Los números de Fibonacci están definidos usando la siguiente relación de recurrencia lineal:

$F_{n}=F_{n-1}+F_{n-2}\,$

con los valores iniciales:

$F_{0}=0\,$

$F_{1}=1\,$

La secuencia de los números de Fibonacci comienza: 0, 1, 1, 2, 3 ,5, 8, 13, 21 ,34, 55, 89... El objetivo de la resolución de la ecuación de recurrencia es encontrar una forma cerrada para calcular los números de Fibonacci.

La ecuación característica es la siguiente:

$x^{2}-x-1=0\,$

$x_{1}={\frac {1+{\sqrt {5}}}{2}}\,$

$x_{2}={\frac {1-{\sqrt {5}}}{2}}\,$

por lo tanto, la solución general es:

$F(n)=A_{1}\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}+A_{2}\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}$

Para hallar el valor de $A_{1}$ y $A_{2}$ resolvemos las siguientes ecuaciones:

$F_{0}=A_{1}\left({\frac {1+{\sqrt {5}}}{2}}\right)^{0}+A_{2}\left({\frac {1-{\sqrt {5}}}{2}}\right)^{0}$

$F_{1}=A_{1}\left({\frac {1+{\sqrt {5}}}{2}}\right)^{2}+A_{2}\left({\frac {1-{\sqrt {5}}}{2}}\right)^{2}$

Entonces:

$A_{1}={\frac {1}{\sqrt {5}}}$

y

$A_{2}={\frac {-1}{\sqrt {5}}}$

La forma cerrada para los números de Fibonacci es:

$F(n)={\frac {1}{\sqrt {5}}}\left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right)$

Ecuación de Recurrencia lineal no homogénea con coeficientes constantes

Recibe el nombre de ecuación de recurrencia lineal no homogénea de grado k, con coeficientes constantes, una expresión del tipo: $c_{0}a_{n}+c_{1}a_{n-1}+c_{2}a_{n-2}+\cdots +c_{k}a_{n-k}=F(n),c_{i}\in \mathbf {R} ,c_{k}\neq 0$.

Resolución

La solución general sería: $a_{n}=a_{n}^{(h)}+a_{n}^{(p)}$ , donde $a_{n}^{(h)}$ es la solución de la ecuación de recurrencia lineal homogénea asociada es decir la ecuación : $c_{0}a_{n}+c_{1}a_{n-1}+c_{2}a_{n-2}+\cdots +c_{k}a_{n-k}=0,c_{i}\in \mathbf {R} ,c_{k}\neq 0$ y donde $a_{n}^{(p)}$ es la solución particular que depende de la función F(n). Por lo tanto los pasos a seguir serían, primero calcular la solución de la ecuación homogénea, calcular una solución particular para F(n) y sumarla a la homogénea, y a continuación aplicar las condiciones iniciales para calcular las constantes. En la siguiente tabla, encontramos cuales son las posibles soluciones particulares:

$F(n)$		${a_{n}}^{(p)}$
$C,{\rm {constante}}$		$C_{0},{\rm {constante}}$
$n$		$C_{0}+C_{1}n$
$n^{2}$		$C_{0}+C_{1}n+C_{2}n^{2}$
$n^{t},t\in \mathbf {Z} ^{+}$		$C_{0}+C_{1}n+\cdots +C_{t}n^{t}$
$r^{n},r\in \mathbf {R}$		$C_{0}r^{n}$
$n^{t}r^{n}$		$r^{n}(C_{0}+C_{1}n+C_{2}n^{2})$
$\sin(An),A\in \mathbf {R}$		$C_{0}\sin(An)+C_{1}\cos(An)$
$\cos(An),A\in \mathbf {R}$		$C_{0}\sin(An)+C_{1}\cos(An)$
$r^{n}\sin(An),A\in \mathbf {R}$		$C_{0}r^{n}\sin(An)+C_{1}r^{n}\cos(An)$
$r^{n}\cos(An),A\in \mathbf {R}$		$C_{0}r^{n}\sin(An)+C_{1}r^{n}\cos(An)$

• Consideraciones:

1.- Si F(n) es una combinación lineal de algunas de las funciones de la tabla anterior, su solución particular es la combinación lineal de las soluciones particulares de esas mismas funciones.

2.- Si uno de los sumandos de F(n) es el producto de una constante por una solución de la ecuación característica homogénea asociada, entonces es necesario multiplicar la solución particular correspondiente a este sumando por la menor potencia de n, n´ tal que este nuevo producto no sea solución de la ecuación característica homogénea asociada.

Ejemplo: Torres de Hanói

La ecuación de recurrencia asociada con el problema de las Torres de Hanói es la siguiente:

$T_{n}=2T_{n-1}+1\,$

Con las condiciones iniciales:

$T_{1}=1\,$

Se resuelve la siguiente homogénea:

$T_{n}^{(h)}=2T_{n-1}$

La ecuación característica es: $x-2=0$, entonces $x=2$

Entonces : $T_{n}^{(h)}=A2^{n}$

A continuación, se resuelve la ecuación particular:$T_{n}^{(p)}=B=2B+1$, entonces $B=-1$.

$T_{n}=A2^{n}-1\,$, entonces igualando con las condiciones iniciales la solución es : $T_{n}=2^{n}-1\,$

Recurrencias No lineales

Para resolver recurrencias no lineales tenemos muchas opciones de las cuales:

• Buscar transformaciones o cambios de variables que hagan la recurrencia lineal.
• Para el caso $t(n)=a\cdot t\left({\frac {n}{b}}\right)+f(n)$ , hay un teorema muy útil que es el Teorema Maestro.

La recurrencia en la computación

La conexión con el análisis de algoritmos estriba en que la forma que se ha adoptado para medir las complejidades, utiliza funciones cuyo dominio son los números naturales, o en otras palabras, sucesiones. Si el algoritmo es recurrente, es de esperarse que las complejidades, como funciones que estiman la demanda de recursos a lo largo de la ejecución, sean sucesiones que satisfacen ciertas ecuaciones de recurrencia. En un algoritmo recursivo, la función t(n) que establece su complejidad viene dada por una ecuación de recurrencia. Una ecuación de recurrencia nos permiten indicar el tiempo de ejecución para los distintos casos del algoritmo recursivo (casos base y recursivo).

Ejemplo : Cálculo del factorial

int Fact(int n){
        if(n<=0)
            return 0;
        else if(n==1)
            return 1;
        return n*Fact(n-1);
}

Considerando el producto como operación básica, podemos construir la ecuación recurrente para calcular la complejidad del algoritmo como sigue:

Como se ve en el código el caso base es para n<=1, para estos valores de n el número de multiplicaciones que se realiza es 0. Y en otro caso es 1 más las necesarias para calcular el factorial de n-1. Así construimos la función recurrente:

$t(n)={\begin{cases}0&{\mbox{si }}n\leq 1\\t(n-1)+1&{\mbox{si }}n>1\end{cases}}$

Ahora si resolvemos la ecuación recurrente sabremos la complejidad de este algoritmo en función de n. Procedemos a resolver esta ecuación recurrente no lineal:

$t(n)=t(n-1)-1\,$

resolvemos la homogénea:

$t(n)=t(n-1)\longrightarrow \quad r-1=0\longrightarrow \quad r=1a_{n}^{h}=c1^{n}\longrightarrow \quad a_{n}^{h}=c$

resolvamos ahora la particular:

como la particular' coincide con la r, debemos aumentar el grado multiplicando por n

$\longrightarrow a_{n}^{p}=n1^{n}\longrightarrow \quad a_{n}^{p}=n$

por lo que la solución de la ecuación recurrente queda como sigue:

$t(n)=c+n\,$

Ahora calculamos c utilizando el caso base, t(1) = 0

$t(1)=c+1=0\longrightarrow \quad c=-1$

ya tenemos la solución: t(n) = n - 1

La ecuación que nos ha quedado es de grado 1 por lo que la complejidad es del orden exacto de n -> θ(n)

Por ejemplo para calcular el factorial de 3 necesitaremos t(3) productos lo que es igual a

$3-1=2\longrightarrow \quad 3\cdot (2\cdot (1))$

Como vemos son 2 productos como nos ha devuelto la ecuación.

Aplicaciones

Entre otras:

• En la óptica
• En la teoría de la probabilidad
• En el estudio de los árboles binarios, pilas y algoritmos de ordenación

Véase también

• Teorema Maestro
• Recursividad