Problemario de Señales y Sistemas/Ancho de banda y rapidez del sistema

← Convolución		Diagramas de Bode. Ancho de banda y rapidez del sistema	Sistemas realimentados →
Problemario de Señales y Sistemas

Ancho de banda y rapidez del sistema

En esta serie de problemas se busca que el estudiante se familiarice con el concepto de ancho de banda y desarrolle el criterio necesario para identificar sistemas de respuesta rápida o lenta según alguna referencia.

Problemas

Problema #1

Se tiene un sistema cuya función de transferencia es:

$H(s)={\frac {15(s/20+1)}{(s+1)(s/5+1)(s/50+1)}}\,$

¿Cuál es la ganancia DC del sistema?
Dibuje el diagrama de polos y ceros
Dibuje el Diagrama de Bode del sistema. Identifique en el diagrama la ubicación de polos y ceros.

Se desea conocer la respuesta del sistema a las siguientes señales

$x(t)=2(\sin(x)-{\frac {\sin(2x)}{2}}+{\frac {\sin(3x)}{3}}\ldots )\,$
$x(t)={\frac {\pi }{2}}+2(\sin(x)+{\frac {\sin(3x)}{3}}+{\frac {\sin(5x)}{5}}\ldots )\,$
$x(t)={\frac {1}{2}}+\sum _{n=1}^{\infty }({\frac {2}{n^{2}\pi ^{2}}}((-1)^{n}-1)\cos(n{\frac {\pi x}{2}})+{\frac {2}{n\pi }}(-1)^{n+1}\sin(n{\frac {\pi x}{2}}))\,$

¿Puede identificar a que señal converge la serie en cada caso?. Use los diagramas de Bode calculados en la primera parte para determinar cuáles de las frecuencias son filtradas por el sistema y cuáles no son atenuadas. Usando sólo las señales que no son atenuadas, grafique un aproximado de la salida del sistema

Subsección 1

Realizado por: Eylin Noguera 05-38629

La ganancia DC es de 15

Diagrama de Polos y Ceros del Sistema

Subsección 2

Realizado por: Romel Torres 05-38996

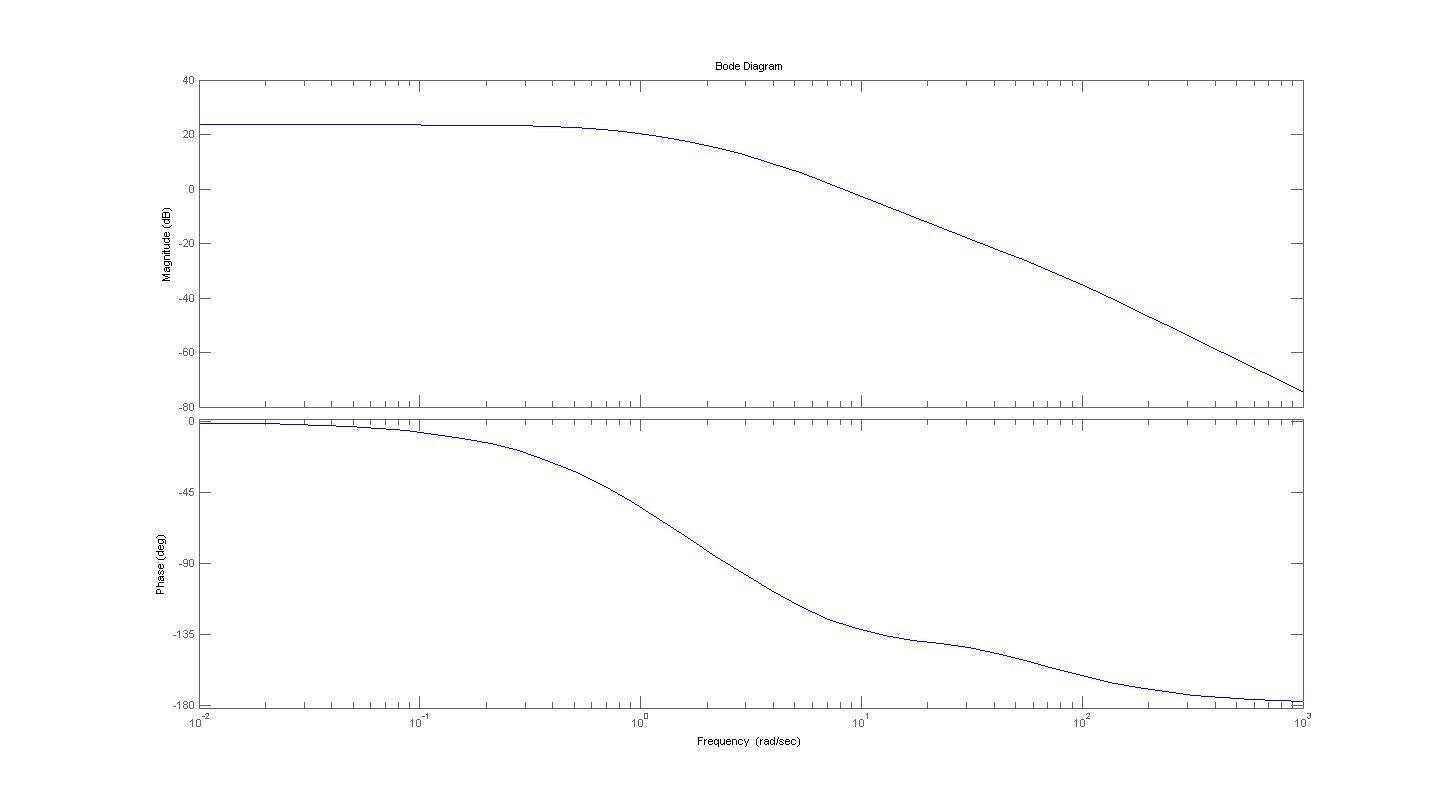
Este es el Diagrama real de Bode de magniud y fase:

En la aproximación a lineas rectas podemos ver mejor, que hay un cero en s=20 y tres polos en: s=-1; s=-5; s=-50.

Podemos ver que para frecuencias altas, el modulo de la respuesta estacionaria del sistema a la señal: == $x(t)=2(sin(t)-sin(2t)+sin(3t)-...)$

empieza a decaer (hacerse más pequeño) de esta manera, sólo necesitamos sumar los primeros 8 terminos de nuestra respuesta en estado estacionario será aproximadamente:

10.41sin(t-54,6°)-6.25sin(3t-81,8°)+4.05sin(3t-97.4°)-2.89sin(4t-107.9°)+2.13sin(5t-115.5°)-1.63sin(6t-120.9°)+1.29sin(7t-125.1°)-1.05sin(8t-128.2°)+...

Entrada

Salida

Subsección 3

Realizado por: Izquiams Martínez 05-38479

Entrada

Como se puede apreciar en la gráfica, la señal #2 converge a un tren de pulsos con un período de aproximadamente 6 unidades de tiempo. Posee una ganancia DC de 0.8 y una amplitud de 1.55. La respuesta del sistema dado a esta señal es como se aprecia en el siguiente gráfico.

Salida

Subsección 4

Realizado por: Eylin Noguera 05-38629

Respuesta del sistema a la señal #3

Entrada

Salida

Problema #2

Considere el sistema que se muestra en el que una señal de entrada $x(t)$ es procesada por un sistema con función de transferencia $G(s)$ para obtener $y(t)$ que luego es amplificada por una ganancia $K$ para obtener $z(t)$ .

La función de transferencia del sistema es:

$G(s)={\frac {50}{(s+10)(s^{2}+s+1)}}\,$ y $K=1\,$

Dibuje el Diagrama de Bode de Magnitud y determine el ancho de banda y el punto de cruce de la ganancia
¿Qué sucede con el ancho de banda y el punto de cruce si la ganancia se aumenta en 10 y se disminuye en 10?
¿En qué caso es sistema es más rápido?

Subsección 1

Realizado por: David Bentolila. Carnet:04-36741

1.-La función de transferencia puede ser reescrita como:

$G(s)={\frac {5}{((s/10)+1)(s^{2}+s+1)}}\,$

Por lo que en el diagrama de Magnitud de Bode vamos a tener cambios de pendiente en w=1 y w=10.

Quedandonos el siguiente diagrama:

-Para hallar el punto de cruce igualamos la ecuación de la recta de pendiente -20 a "0".

Ec. de la recta:

20log(5)-20log(w)=0, la solución a esta ecuación es w=5.

-Para hallar el ancho de banda igualamos la ecuación de la recta dependiente -20 a 20log(5)-3

20log(5)-20log(w)=20log(5)-3, por lo tanto 20log(w)=3, y esta igualdad se cumple para w=1.413 que corresponde al ancho de banda.

Subsección 2

Xavier Perez 0437405

Consideramos para el primer caso una ganancia 10, entonces la funcion de transferencia quedaría:

$H(s)={\frac {50}{((s/10)+1)(s^{2}+s+1)}}\,$

El diagrama de Bode es muy parecido al de la parte A, con la diferencia de que este último empieza en 33.98 dB. El ancho de banda es EL MISMO. Esto se debe a que la caida de 3 dB con relacion a la ganancia en o se da en el mismo punto w=1.41 . Para el punto de corte, en éste caso debemos usar la ecuación de la recta de pendiente 13.98-60log(w/10)=0, w=16.98

Para el segundo caso, tomamos la ganancia reducida en 10 veces:

$H(s)={\frac {0.5}{((s/10)+1)(s^{2}+s+1)}}\,$

De nuevo el diagrama es muy parecido, pero en esta ocasión comienza en el semiplano inferior, específicamente en -6dB. La frecuencia de ancho de banda es la misma(w=1.41). Este diagrama no corta con el punto de ganancia 0, ya que esta es siempre negativa.

Subsección 3

Xavier Perez 0437405

Al comparar los diagramas de fase se observa que el más rápido es el de la ganancia aumentada en 10, ya que para frecuencias mas altas todavía tiene una ganania considerable cuando los otros ya la han bajado en gran proporción.

Problema #3

Para las funciones de transferencia que se muestran a continuación dibuje los diagramas de polos y ceros, indique los sistemas que son estables o no y dibuje los diagramas de Bode aproximados y exactos. ¿Cuáles son las similitudes y cuáles las diferencias en sus respuestas frecuenciales?

$H_{1}(s)={\frac {s+1}{s^{2}+2s+5}}\,$
$H_{2}(s)={\frac {s-1}{s^{2}+2s+5}}\,$
$H_{3}(s)={\frac {s+1}{s^{2}-2s+5}}\,$

Andreina Benezra 05-37901

Para H1(s): # $H_{1}(s)={\frac {s+1}{s^{2}+2s+5}},$ tenemos los siguientes polos complejos conjugado S1= -1+j2, S2=-1-j2. Estos polos se encuentran en el semiplano izquierdo lo que significa que el sistema es estable. Tenemos un cero en s=-1

Para H2(s): # $H_{2}(s)={\frac {s-1}{s^{2}+2s+5}}\,$ tenemos los siguientes polos complejos conjugado S1= -1+j2, S2=-1-j2. Estos polos se encuentran en el semiplano izquierdo lo que significa que el sistema es estable. Tenemos un cero en s=1, este cero en el plano derecho añade un comportamiento inverso pero no inestabilidad.

Para H3(s): # $H_{3}(s)={\frac {s+1}{s^{2}-2s+5}}\,$ tenemos los siguientes polos complejos conjugados S1= 1+j2, S2=1-j2. Estos polos se encuenran en el semiplano derecho lo que significa que el sistema es inestable. Tenemos un cero en s=-1.

En cuanto a la respuesta frecuencial se puede observar que la magnitud para los tres casos es la misma. Sustituyendo s=jw en H1(s), H2(s), H3(s) tenemos:

# $H_{1}(jw)=H_{2}(jw)={\frac {1/5(w^{2}+1)^{1}/2}{((1-w^{2}/5)^{2}+4w^{2}/25)^{1}/2}}\,$

La diferencia esta en la fase.

En el caso de H1(s): El cero ubicado en 1 introduce un desfasaje de 90º mientras que el cero en raiz de 5 (frecuencia fundamental) introduce un desfasaje -180º.

En el caso de H2(s): H_2(s)=tg^-1 w/-1 - tg^-1 {(2/5w)/(1-w^2/5)}. El primer termino hace que todos los angulos esten en el segundo cuadrante.

En el caso de H3(s): H_3(s)=tg^-1w/1 - tg^-1 {(-2/5w)/(1-w^2/5)}. Para W=0 empieza en -360º y para W=infinito termina en -180º.

Mayra Castellanos 05-37997