Problemario de Señales y Sistemas/Señales Periódicas
Señales Periódicas
[editar]En esta serie de problemas se busca que el estudiante se familiarice con el concepto período, frecuencia y suma de señales periódicas (cuando son señales sinusoidales, ¿puede extenderse a la multiplicación?.
Problemas
[editar]Problema 2 02 08
[editar]Para las señales que se listan a continuación determine cuáles son periódicas y cuáles no. Para las señales periódicas calcule su período y frecuencia (rad/s), su área absoluta, energía, potencia y valor RMS en un período. En todos los casos grafique la señal en el intervalo -6<t<6. Si hubiera señales complejas grafique parte real e imaginaria.
Problema #1
[editar]Para las señales que se listan a continuación determine cuáles son periódicas y cuáles no. Para las señales periódicas calcule su período y frecuencia (rad/s), su área absoluta, energía, potencia y valor RMS en un período. En todos los casos grafique la señal en el intervalo -6<t<6. Si hubiera señales complejas grafique parte real e imaginaria.
Problema #1. Subproblema 1=
[editar]Realizado por Esteban Bacilio 05-37871
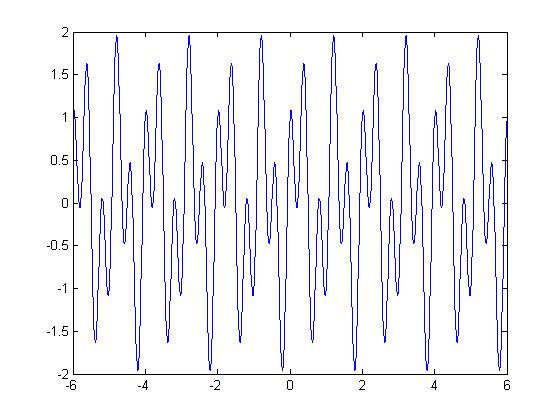
Se tienen w1=1/3; w2=1/2; w3=2;. Se puede ver que la razón de cualquier par de frecuencias individuales es una fracción racional => la señal es periódica.
La frecuencia natural wn es el MCD de las frecuencias individuales: wn=MCD(1/3,1/2,2)=1/6 rad/seg.
El período natural correspondiente Tn=2/wn=2/(1/6)=12
La Potencia de la señal X1(t) es la suma de las potencias individuales:
El valor rms de la señal:
Entonces la energía en un período Tn:
La gráfica de esta señal es la siguiente:
a) Para un tiempo entre -6 < t < 6
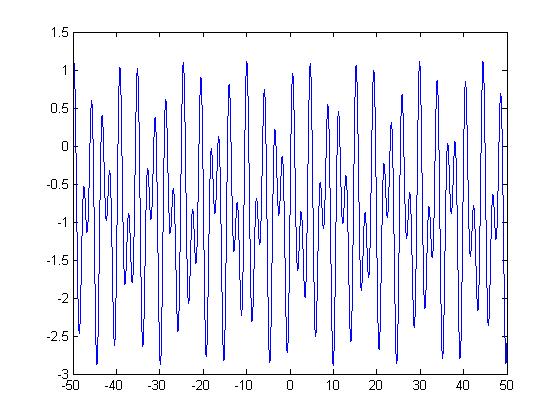
b) Para un tiempo entre -80 < t < 80 ( En donde podemos apreciar la frecuencia y periodo fundamental.
Problema #1. Subproblema 2=
[editar]Realizado por Esteban Bacilio 05-37871
como
nos queda:
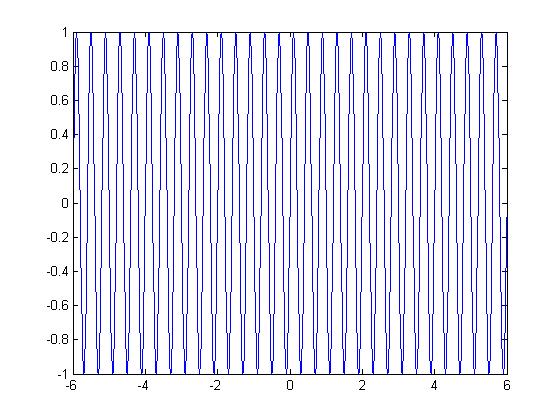
Parte real. Se tienen w1=2 y w2=5, entonces, como la razón de ambas frecuencias es un número racional: w1/w2=2/5 => la parte real de la señal es periódica.
La frecuencia natural wn de la parte real: El período, Tn=2.
La Potencia de esta señal en un período Tn es la suma de las potencias individuales:
El valor rms de la señal (para la parte real):
La energía en un período Tn:
La gráfica de la parte real de la función para un intervalo de tiempo entre -6 < t < 6:
Parte imaginaria. La señal está dada por un solo seno => es periódica
La gráfica de la parte imaginaria:
Problema #1. Subproblema 3
[editar]Realizado por Euro Rivero 03-36396
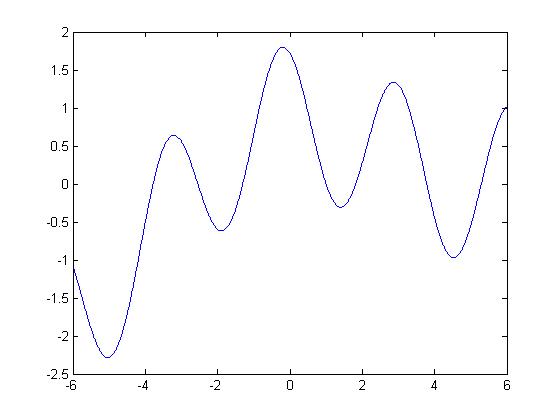
Se tienen las frecuencias individuales: w1=3 w2= w3=
La razón entre un par de frecuencias: w1/w2= nos da un número no racional => la señal no es periódica.
La gráfica de esta señal es:








![{\displaystyle P=P_{1}+P_{2}+P_{3}={\frac {1}{Tn}}\int _{0}^{Tn}\sin \left({\frac {1}{3}}t\right)dt+{\frac {1}{Tn}}\int _{0}^{Tn}\cos \left({\frac {1}{2}}t+{\frac {\pi }{5}}\right)dt+{\frac {1}{Tn}}\int _{0}^{Tn}\sin(2t+2)dt={\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}={\frac {3}{2}}[W]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06eaa5bcf3b4e276e47eb596ba470a148c5656a4)

![{\displaystyle E=Tn.P=18[J]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc85e07518a047792b083b1efa3034573963a508)




![{\displaystyle P=P_{1}+P_{2}={\frac {1}{Tn}}\int _{0}^{Tn}\sin(2\pi t)dt+{\frac {1}{Tn}}\int _{0}^{Tn}\cos(5\pi t)dt={\frac {1}{2}}+{\frac {1}{2}}=1[W]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbb737cf42e69beef5e7a509fd8f104577e764cc)

![{\displaystyle E=Tn.P=2[J]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d335fbbac24cd80e678d1c9aad5eff5da19510f)