		Sonido en el Dominio Temporal	Sonido en el Dominio Digital →
Teoría de la Síntesis de Sonido

El Sonido en el Dominio Temporal

La apariencia y el comportamiento de las ondas de sonido

La definición métrica (acústica) del sonido es la variación en las ondas de presión y la densidad causada por la propagación de las ondas a través de un medio. Entre aproximadamente 25 Hz y 18 kHz, los sistemas auditivos humanos detectan estas ondas ya que hacen que el tímpano se mueva. Este movimiento mecánico se transduce en señales electroquímicas en la cóclea como impulsos nerviosos, y se envía a la región auditiva del cerebro para su análisis. Las ondas sonoras, que son variaciones en la presión del aire a lo largo del tiempo, pueden representarse como una tensión variable o como una corriente de datos a lo largo del tiempo. Esta es una representación del sonido en 'tiempo/amplitud', también conocida como línea de tiempo de amplitud. La amplitud representa el desplazamiento molecular causado por los cambios en la presión del aire. En el dominio digital, la amplitud se representa típicamente como un valor entre 1 y -1 donde 1 y -1 representan las máximas amplitudes positiva y negativa de la señal, y 0 representa cero amplitud.

**Figura 1.1**. Una forma de onda sinusoidal simple representada como amplitud variable a lo largo del tiempo.

La forma de onda en la Fig. 1.1 se llama onda sinusoidal o sinusoide. Las ondas sinusoidales pueden considerarse los bloques de construcción fundamentales del sonido. La figura demuestra que la amplitud varía con el tiempo, pero ese patrón de varianza se repite periódicamente.

**Figura 1.2**. Una forma de onda más compleja.

La forma de onda en la Fig. 1.2 es más complicado que la sinusoide en 1.1. Hay picos y valles (la parte más alta y la parte más baja) de diferentes amplitudes, y, aunque el patrón se repite con el tiempo (mira si puedes encontrarlo) es más difícil de detectar. De la misma manera que una onda sinusoidal se comporta de una manera simple y suena simple, este sonido se comporta con mayor complejidad y también suena más complejo. Por esta razón, los sonidos detallados y complejos que cambian con el tiempo a menudo no tienen características discernibles cuando se ven de cerca; puede que no haya un patrón o comportamiento repetitivo que podamos usar para decirnos algo sobre el sonido.

**Figura 1.3**. Un gráfico en el dominio temporal de un kit de batería a través de 2 segundos.

En la Fig. 1.3 damos un vistazo a un sonido en el transcurso de aproximadamente 2 segundos en lugar de 2 milisegundos. Desde esta perspectiva, podemos ver la forma en que la amplitud del sonido general cambia con el tiempo; en particular, las partes con gran amplitud se pueden ver fácilmente como golpes de batería: aparecen de repente y caen en amplitud muy rápidamente, como cabría esperar al golpear la cabeza de un tambor. Puede haber sido muy difícil decir qué tipo de instrumento se estaba reproduciendo si este sonido se visualizara en el rango de unos pocos milisegundos. A partir de esto, debemos concluir que las perspectivas de intervalo de tiempo corto e intervalo de tiempo largo muestran diferentes tipos de información y que la selección de la perspectiva correcta para satisfacer nuestras necesidades es importante.

Sinusoides, Frecuencia y Tono

Como se indica en Fig. 1.1, la onda sinusoidal tiene una forma periódica que se repite cada $T\,$ segundos que se conoce como el período, ciclo. La onda también tiene una amplitud máxima positiva, $A\,$ y una amplitud máxima negativa, $-A\,$ . La frecuencia, $f\,$ de una onda senoidal es el número de ciclos por segundo y se mide en Hertz (Hz). Podemos obtener la frecuencia de la longitud de onda de la siguiente ecuación:

f={\frac {1}{T}}\,

Además, podemos expresar una onda sinusoidal con la siguiente forma matemática (con ángulos en radianes). Esta forma puede ser útil para los programadores interesados en crear sus propias funciones senoiales controlables en el código:

p(t)=Asin\left({\frac {2\pi t}{T}}\right)=Asin(2\pi ft)

Psicométricamente, las frecuencias más altas (por ejemplo, más de 1,5 kHz) a menudo se asocian con palabras como 'brillo', mientras que las frecuencias más bajas (por ejemplo, por debajo de 200 Hz) a menudo se asocian con 'profundidad' o 'bajo'. El rango intermedio puede estar asociado con el término 'calidez'. Por ejemplo, un instrumento como una guitarra eléctrica que se tocó limpio puede llamarse 'brillante' o 'nítido', mientras que un contrabajo acústico puede denominarse 'oscuro' y 'cálido'. Siendo psicométricos, términos como estos no son cantidades objetivas que podamos medir con precisión, pero a menudo se usan para describir el "timbre" o el color tonal de un sonido en particular. Las diversas amplitudes de frecuencias presentes en un sonido y su evolución en el tiempo son los principales factores asociados con el timbre, y hay infinitos tonos de timbre que se pueden lograr a través de combinaciones de diferentes frecuencias que componen un sonido. En términos psicométricos, el oído humano asocia relaciones de frecuencia de números enteros con "tono" y asocia frecuencias particulares con notas particulares en la escala occidental estándar:

Longitud de onda (t)	Frecuencia (Hz)	Nombre de la nota
156.82 cm	220.0	A3
139.71 cm	246.94	B3
131.87 cm	261.63	C4
117.48 cm	293.66	D4
104.66 cm	329.63	E4
98.79 cm	349.23	F4
88.01 cm	392.0	G4
78.41 cm	440.0	A4

Fig. 1.4. La relación entre la longitud de onda, la frecuencia y el nombre de la nota.

Ten en cuenta que esta tabla cubre el rango de una octava. La frecuencia se duplica y la longitud de onda se divide en mitades.

Construcción y deconstrucción de sinusoides

Usando el análisis de Fourier, las ondas sinusoidales pueden considerarse los componentes fundamentales del sonido, ya que una sola onda sinusoidal es una sola frecuencia. Dentro del análisis de Fourier, la combinación de sinusoides de diferente frecuencia, amplitud y fase puede recrear el espectro de frecuencia de cualquier sonido. Del mismo modo, los sonidos complejos pueden analizarse en términos de frecuencias, amplitudes y fase.

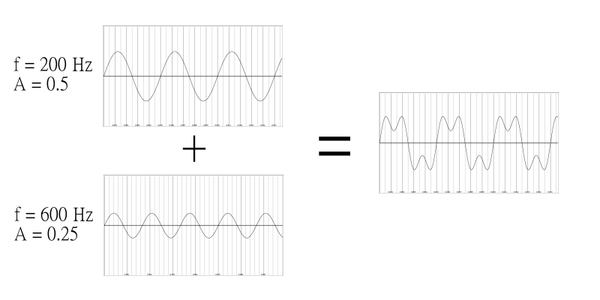
La Fig. 1.5 demuestra la apariencia de dos ondas sinusoidales sumadas. Las características de ambas ondas se combinan en la forma de onda resultante. Esta técnica es la base de la síntesis aditiva que se trata más adelante en el libro. Además, en la forma en que se construye el sonido, es posible filtrar las dos frecuencias componentes del todo; esto se hace típicamente mediante el análisis de la forma de onda en el dominio frecuencial, que se trata en el capítulo siguiente.