Wikichicos/Geometría/Capítulo 13. Construcciones: Regla y compás

En esta sección aprenderemos a construir líneas y figuras con regla y compás.

Esta es una imagen de un compás y una regla.

Cómo dibujar una línea

Usando una regla podemos dibujar un segmento de recta

Utilizaremos la notación${\overline {AB}}$ para el segmento de recta que empieza en A y acaba en B. Obsérvese que no nos importa la dirección del segmento y, por tanto, ${\overline {AB}}$ es lo mismo que ${\overline {BA}}$.

Segmento de línea ${\overline {AB}}$

Segmento de línea ${\overline {BA}}$

Cómo dibujar un círculo

• Usando el compás

Usamos la notación $\circ A,{\overline {AB}}$ para la circunferencia cuyo centro es el punto A y su longitud de radio es igual a la del segmento ${\overline {AB}}$.

La notación centro-radio se eligió por su idoneidad para construir círculos con regla y compás.

Cómo trazar líneas paralelas a otra

• Utilizamos la regla y la escuadra.
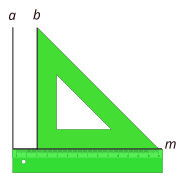
• Situamos la regla de forma vertical al papel y situamos al lado de ella la escuadra (fig.1)
• Trazamos una recta siguiendo la escuadra y sin mover la regla (recta a)
• Desplazamos la escuadra hacia abajo y vamos trazando las líneas que queramos (figs. 2, 3 y 4)

• 
  fig. 1
• 
  fig. 2
• 
  fig. 3
• 
  fig. 4

Cómo trazar líneas perpendiculares a otra

• Utilizamos la regla y la escuadra.
• Situamos la regla de forma horizontal al papel y trazamos la línea $m$ (fig.1)
• Situamos al lado de ella la escuadra (fig.1)
• Trazamos una recta siguiendo la escuadra y sin mover la regla (recta a)
• Desplazamos la escuadra hacia la derecha y vamos trazando las líneas que queramos (figs. 2 y 3 )

• 
  fig. 1
• 
  fig. 2
• 
  fig. 3

Cómo trazar una línea perpendicular a otra utilizando el compás

1. Trazamos un recta horizontal y en ella marcamos dos puntos $A$ y $B$ distantes lo que queramos. Serán los centros de las circunferencias que trazaremos´.
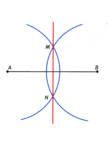
2. Con centro en $A$ y con una abertura del compás mayor que la mitad del segmento marcado en la recta se traza una circunferencia que vaya de arriba a abajo del segmento (en color azul en la imagen).
3. Con centro en $B$ se traza otra circunferencia como anteriormente.
4. Estas circunferencias determinan al cortarse los puntos $M$ y $N$
5. Unimos con una recta estos puntos y ya tenemos la mediatriz del segmento perpendicular a la recta.

• 
  Tramos un segmento y el arco de circunferencia
• 
  Estos arcos determinan al cortarse los puntos de la mediatriz
• 
  Unimos con una recta estos puntos

Cómo dibujar la bisectriz de un ángulo

Dibujar la bisectriz de un ángulo

1. Trazamos el ángulo que queramos
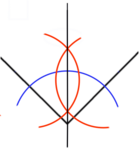
2. Con el compás hacemos centro en el vértice y trazamos una circunferencia que pase aproximadamente por el centro de los lados del ángulo (en azul en la imagen 2)
3. Hacemos centro con el compás en la intersección de la circunferencia azul con uno de los lados y trazamos un arco que corte a la circunferencia azul (arco rojo, fig. 3).
4. Hacemos lo mismo desde la otra intersección del otro lado (el otro arco rojo) y vemos que los arcos rojos se cortan en dos puntos que serán por donde pase la bisectriz

• 
  Trazamos un ángulo
• 
  Trazamos la circunferencia
• 
  Trazamos el arco rojo
• 
  Trazamos el otro arco rojo
• 
  Unimos los puntos de corte

Cómo trazar un ángulo recto o una perpendicular en el extremo de un segmento

Trazar un ángulo recto o una perpendicular en el extremo de un segmento

1. Trazamos la recta $h$ con un punto $A$ en un extremo
2. Señalamos un punto $M$ fuera de la recta.
3. Con una abertura de compás igual a la distancia desde el punto al extremos $A$ del segmento trazamos una circunferencia que pase por $A$ ( punto $P$ )
4. La circunferencia cortará a la recta en un punto $B$
5. Se une el punto $M$ con $B$ y se prolonga la recta hasta que corte a la circunferencia en otro punto $P'$.
6. Uniendo este punto $P'$ con el extremo del segmento $A$ tendremos la perpendicular y el ángulo recto.

Construcción de un triángulo conociendo la medida de sus tres lados

1. Trazamos los lados que formarán el triángulo: $a$, $b$ y $c$
2. Trazamos el lado más largo $a$ debajo, como base.
3. Con una abertura de compás igual a la distancia desde un extremo de $b$ a su otro extremo y haciendo centro en un extremo de $a$ (punto verde) trazamos una circunferencia (roja en el ejemplo).
4. Con una abertura de compás igual a la distancia desde un extremo de $c$ al otro extremo y haciendo centro en el otro extremo de $a$ (punto verde) trazamos otra circunferencia (roja en el ejemplo).
5. El punto de cruce de las dos circunferencias será el vértice que faltaba. Con la regla llevaremos los segmentos $b$ y $c$ desde $a$ hasta el punto de cruce y ya está trazado el triángulo.

• 
  Trazamos los lados y la circunferencia (fg.1)
• 
  Trazamos la otra circunferencia (fg.2)
• 
  Unimos con el vértice (fg.3)

Construcción de un hexágono regular

1. Trazamos una línea horizontal y un punto en ella aproximadamente en su centro (fig 1)
2. Haciendo centro en el punto elegido trazamos con el compás una circunferencia tomando como radio la longitud a un extremo de la línea. (fig 1)
3. Haciendo centro en el punto donde se cortan la línea y la circunferencia trazamos una semicircunferencia con radio igual al de la circunferencia primera (semicircunferencia verde) (fig. 1)
4. Hacemos lo mismo pero desde el otro punto de la línea en el cruce con la circunferencia (la otra semicircunferencia verde)
5. Ya tenemos los seis vértices del hexágono. Los unimos con segmentos y ya tenemos el hexágono regular (fig.2, 3 y 4)

• 
  Trazamos la línea, el punto y las circunferencias (fg.1)
• 
  Unimos los vértices (fg.2)
• 
  Unimos los vértices (fg.3)
• 
  El hexágono regular (fg.)

Construcción de un triángulo equilátero

Introducción

Triángulo equilátero

En este capítulo te enseñaremos a dibujar un triángulo equilátero. ¿Qué significa "equilátero"? Significa simplemente que los tres lados del triángulo tienen la misma longitud.

Cualquier triángulo cuyos vértices (puntos) sean A, B y C se escribe así: $\triangle ABC$.

Y si es equilátero, se parecerá al de la imagen.

La construcción

1. Usando tu regla, dibuja un segmento de cualquier longitud que quieras que tengan los lados de tu triángulo.
   Llama un extremo del segmento de línea A y el otro extremo B.
   Ahora tienes un segmento de línea llamado ${\overline {AB}}$.
   Debería parecerse al dibujo siguiente.
   
2. Usando tu compás, dibuja el círculo $\circ A,$ cuyo centro es A y el radio es ${\overline {AB}}$.
   
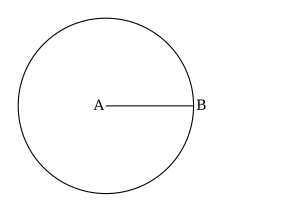
3. Nuevamente usando tu compás dibuja el círculo $\circ B,{\overline {AB}}$, cuyo el centro es B y el radio es ${\overline {AB}}$.
   
4. ¿Puedes ver cómo los círculos se cruzan (se cruzan entre sí) en dos puntos?
   Los puntos se muestran en rojo en la imagen de abajo.
   
5. Elegimos uno de estos puntos y lo llamamos C.
   Elegimos el punto superior, pero usted puede elegir el punto inferior si lo desea. Si eliges el punto inferior, tu triángulo parecerá al revés, pero seguirá siendo un triángulo equilátero.
   
6. Dibuja un segmento entre A y C y obtener el segmento de línea ${\overline {AC}}$.
   
7. Dibuja un segmento entre B y C y obtener el segmento de línea ${\overline {BC}}$.
   
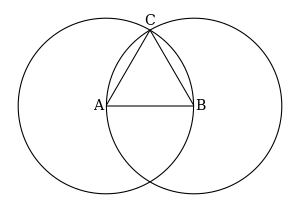
8. Se completa la construcción de $\triangle ABC$.

....................................................................................................................................................