Wikichicos/Geometría/Capítulo 3. Triángulos

Un triángulo es una forma geométrica (polígono) que posee tres lados y tres ángulos. Un triángulo tiene tres ángulos interiores, tres lados y tres vértices entre otros elementos.
Elementos
[editar]
Vértices
[editar]
Los vértices son cada uno de los puntos que determinan un triángulo, los puntos donde se cortan dos lados. Tal como los vértices de un polígono, suelen ser denotados por letras latinas mayúsculas: .
Un triángulo se nombra designando sucesivamente sus vértices, por ejemplo ABC. En el caso del triángulo, los vértices pueden darse en cualquier orden, por cualquiera de las 6 maneras posibles (ABC, ACB, BAC, BCA, CAB, CBA), corresponde a un recorrido de su perímetro.
Lados
[editar]
Cada par de vértices determina un segmento, que se conoce como lado del triángulo. No importa el orden de los vértices para nombrar un lado de modo que AB y BA nombran a un mismo lado.
Los lados del triángulo se denotan, como todos los segmentos, por sus extremos: AB, BC y AC.
Para nombrar la longitud de un lado, por lo general se utiliza el nombre del vértice opuesto, convertido a minúscula latina: para BC, para AC, para AB.
La suma de los lados de un triángulo se conoce como perímetro, denotado por p ; cumple la ecuación:
Ángulos
[editar]
Cada par de lados con origen común al vértice de un triángulo y que contienen dos de esos lados concurrentes se llama ángulo del triángulo u -ocasionalmente- ángulo interior.
La notación general para el ángulo entre dos lados es con una letra minúscula (del alfabeto español o del alfabeto griego) colocada entre los lados que forman el ángulo y cerca del vértice.[1]
La suma de los ángulos de un triángulo es igual a 180º
Altura
[editar]Se llama altura de un triángulo al segmento de recta perpendicular que une un vértice del triángulo con el lado opuesto de este o su prolongación. El lado opuesto se llama base del triángulo. Se suele escribir como h
Clasificación de los triángulos
[editar]Los triángulos pueden clasificarse de dos formas:
Por la amplitud de sus ángulos
[editar]
- Acutángulo: sus tres ángulos son menores a 90°.
- Rectángulo: uno de sus ángulos es de 90°.
- Obtusángulo: tiene un ángulo mayor a 90°.
Por la longitud de sus lados
[editar]
- Equilátero: todos sus lados son iguales.
- Isósceles: tiene dos lados iguales, y uno distinto.
- Escaleno: todos sus lados son diferentes entre ellos.
Los triángulos también pueden ser
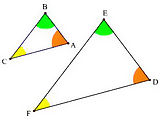
[editar]- Semejantes: son los que tienen la misma forma pero distinta extensión.
- Simétricos: son los que tienen la misma forma pero colocadas en distinto sentido
-
Triángulos semejantes
-
Triángulos simétricos
Área del triángulo
[editar]
El área del triángulo es igual a la mitad del producto de su base por su altura.
La formula se escribe así: (base por altura dividido por dos)

Hallar el área de un triángulo
Hallar el área de un triángulo que mide 4 cm de base y 5 cm de altura

Aplicando la fórmula (base por altura dividido por dos)
El triángulo rectángulo
[editar]
Un triángulo rectángulo es el que tiene un ángulo de 90 grados. Los otros dos ángulos siempre suman 90 grados, pero pueden ser de distinto tamaño. El lado opuesto al ángulo recto es la hipotenusa; es el lado más largo del triángulo rectángulo. Los otros dos lados son los catetos del triángulo.
Los lados o ángulos que faltan en un triángulo rectángulo pueden hallarse utilizando el teorema de Pitágoras. En cualquier triángulo todos los ángulos suman 180 grados.
Teorema de Pitágoras
[editar]
Υ2+β2= ᾳ2. El cuadrado rojo tiene 16 cuadrados de área, el amarillo 9 y el correspondiente a la hipotenusa 25, que es la suma 16 + 9
El teorema de Pitágoras es una afirmación sobre los lados de un triángulo rectángulo.
Afirmación de la teoría
[editar]El teorema de Pitágoras dice que el área de un cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos.
En la imagen de la derecha, el área del cuadrado rojo sumada al área del cuadrado amarillo es igual al área del cuadrado de la hipotenusa. Debe su nombre al matemático griego Pitágoras:
Si las longitudes de los catetos son a y b, y la longitud de la hipotenusa es c, entonces se cumple que .
Aplicación de la teoría
[editar]
Hallar la hipotenusa de un triángulo rectángulo
Hallar la hipotenusa de un triángulo rectángulo cuyos catetos miden: 3 cm en cateto menor y 4 cm el cateto mayor.

Aplicando la fórmula: hipotenusa c2 = cateto a2 + cateto b2
= + ;
= ;
Referencias
[editar]
.....................................................................................................................................................
Ejercicios
[editar]
....................................................................................................................................................