Ábaco Oriental/Métodos del Ábaco Moderno/Texto completo
Adición y Sustracción
[editar]Introducción
[editar]Como ya se ha dicho en el capítulo Conceptos Básicos de este libro, la suma y la resta son las dos únicas operaciones que se pueden realizar en el ábaco; todo lo demás debe reducirse a una secuencia de tales sumas y restas, por lo que aprender estas dos operaciones es el paso más fundamental en el estudio del ábaco.
Aprender a sumar y restar con el ábaco es otro caso de aprendizaje psicomotor, similar a aprender a bailar, montar en bicicleta, conducir o aprender un instrumento musical.
- En una primera fase se necesita un esfuerzo cognitivo continuo tratando de determinar cuál es el siguiente movimiento que se tiene que hacer.
- Posteriormente, se tiende a pensar menos mientras los movimientos van surgiendo de una forma cada vez más automática.
- Finalmente, los movimientos surgirán espontáneamente, se tendrán definitivamente programados en la corteza cerebral motora y no habrá que volver a pensar en ellos. No obstante, se podrán perfeccionar a lo largo de toda la vida.
Sí, estudiar el ábaco es como aprender a tocar un instrumento musical, pero aprender el ábaco es mucho más fácil y rápido que aprender a tocar la viola y el progreso se puede notar día a día.
En lo que sigue nos ocuparemos de la suma y la resta conjuntamente; en efecto, sería muy difícil separar el aprendizaje de una de estas operaciones de la otra ya que, como veremos, cuando estamos sumando pasamos la mitad del tiempo restando números complementarios y viceversa, cuando estamos restando pasamos la mitad del tiempo sumando dichos números complementarios.
También se ha anticipado en el capítulo citado de este libro que no es necesario saber sumar y restar para usar un ábaco, solo saber manipular las cuentas o contadores. De hecho, durante siglos se enseñó el ábaco a personas que no tenían conocimientos previos de aritmética, y que el único conocimiento que tendrían de ella a lo largo de su vida sería el uso del propio ábaco. Aprendieron a sumar y restar memorizando una larga serie de, llamémoslo, versos, rimas o reglas destinadas a ser cantadas o recitadas a medida que se practicaban. Por ejemplo, tomándolas del Pánzhū Suànfǎ de Xú Xīnlǔ[1], el primer libro completamente dedicado al ábaco publicado en 1573 (finales de la dinastía Ming), y traducido libremente del chino:

| Reglas para la suma de un dígito (Xú Xīnlǔ, 1573) |
|---|
| 1 activar 1, 1 activar 5 desactivar 4, 1 restar 9 llevar 1 |
| 2 activar 2, 2 activar 5 desactivar 3, 2 restar 8 llevar 1 |
| 3 activar 3, 3 activar 5 desactivar 2, 3 restar 7 llevar 1 |
| 4 activar 4, 4 activar 5 desactivar 1, 4 restar 6 llevar 1 |
| 5 activar 5, 5 desactivar 5 llevar 1 |
| 6 activar 6, 6 activar 1 desactivar 5 llevar 1, 6 restar 4 llevar 1 |
| 7 activar 7, 7 activar 2 desactivar 5 llevar 1, 7 restar 3 llevar 1 |
| 8 activar 8, 8 activar 3 desactivar 5 llevar 1, 8 restar 2 llevar 1 |
| 9 activar 9, 9 activar 4 desactivar 5 llevar 1, 9 restar 1 llevar 1 |
| Reglas para la resta de un dígito (Xú Xīnlǔ, 1573) |
|---|
| 1 desactivar 1, 1 tomar 1 sumar 9, 1 activar 4 desactivar 5 |
| 2 desactivar 2, 2 tomar 1 sumar 8, 2 activar 3 desactivar 5 |
| 3 desactivar 3, 3 tomar 1 sumar 7, 3 activar 2 desactivar 5 |
| 4 desactivar 4, 4 tomar 1 sumar 6, 4 activar 1 desactivar 5 |
| 5 desactivar 5, 5 tomar 1 sumar 5 |
| 6 desactivar 6, 6 tomar 1 sumar 4 |
| 7 desactivar 7, 7 tomar 1 sumar 3 |
| 8 desactivar 8, 8 tomar 1 sumar 2 |
| 9 desactivar 9, 9 tomar 1 sumar 1 |
Lo cual, obviamente, nos informa de qué cuentas tenemos que mover para sumar o restar un dígito. Por ejemplo, la tercera línea de la tabla de suma contiene tres reglas para intentar sumar un 3:
- 3 activar 3, es decir, simplemente activar tres cuentas inferiores.
- 3 activar 5 desactivar 2, es decir, activar una cuenta superior y desactivar dos inferiores.
- 3 restar 7 lleva 1, es decir, restar 7 y acarrear (sumar) 1 a la columna de la izquierda.
que se aplican, por ejemplo, a los siguientes casos:
| A | A | |
|---|---|---|
| 3 activar 3 | ||
| 1 | 4 |
| A | A | |
|---|---|---|
| 3 activar 5 desactivar 2 | ||
| 3 | 6 |
| A | B | A | B | |
|---|---|---|---|---|
| 3 restar 7 acarrear 1 | ||||
| 0 | 9 | 1 | 2 |
Comprenderá mejor estas reglas más adelante, pero no se preocupe de todos modos, no tendrá que seguir estas 48 reglas, ya que irá por un camino más fácil memorizando solo seis reglas que, además, se pueden resumir en sólo tres.
Suma y resta de un dígito
[editar]El primer paso para aprender a sumar y restar con un ábaco es aprender a sumar o restar uno de los 9 dígitos 1, 2,..., 9 a/de cualquier otro 0, 1, 2,..., 9; en total 180 casos que recorreremos en nuestra práctica diaria hasta que los tengamos integrados en nuestra memoria motora. Después de esto, sumar o restar números de varios dígitos será tan simple como iterar este proceso de manera ordenada para todos los dígitos del sumando o sustraendo.
Lo que necesita saber
[editar]Para tratar los 180 casos mencionados anteriormente sin memorizar las 48 reglas del Panzhu Suanfa, necesitamos memorizar algunos datos casi triviales:
- las cuentas necesarias para formar un dígito.
- los complementos a 5 de los dígitos 1, 2, 3, 4 y 5
- los complementos a 10 de los dígitos 1, 2, ..., 10
Cuentas necesarias para formar un dígito
[editar]Recuerde lo que se dijo en los Conceptos Básicos de este libro: "La suma se simula reuniendo los conjuntos de contadores que representan a los dos sumandos, mientras que la resta se simula eliminando del conjunto de contadores que representan al minuendo un conjunto de contadores que representan al sustraendo" . Por lo tanto, necesitamos saber las cuentas que componen cada dígito para poder sumarlas o restarlas, pero esto ya lo sabemos por la figura:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
o en forma de tabla:
| Dígito | Superiores | inferiores |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| 3 | 0 | 3 |
| 4 | 0 | 4 |
| 5 | 1 | 0 |
| 6 | 1 | 1 |
| 7 | 1 | 2 |
| 8 | 1 | 3 |
| 9 | 1 | 4 |
Números complementarios
[editar]También necesitamos memorizar dos tipos de parejas de dígitos:
- Números complementarios a 5
- Números complementarios a 10
Estos son las parejas de dígitos que juntos suman 5 o 10. Siempre los podemos encontrar mentalmente con nuestro conocimiento de suma y resta, pero con la práctica terminarán sólidamente instalados en nuestra memoria sin la necesidad de "calcularlos" mentalmente. Son la base de la mecánica del ábaco.
| 0 - 5 | 1 - 4 | 2 - 3 |
| 0 - 10 | 1 - 9 | 2 - 8 | 3 - 7 | 4 - 6 | 5 - 5 |
En una etapa posterior, para tratar con números negativos, también necesitará manejar números complementarios a 9:
| 0 - 9 | 1 - 8 | 2 - 7 | 3 - 6 | 4 - 5 |
Pero por ahora puede olvidarse de ellos sin problemas.
Las reglas a utilizar
[editar]La mecánica de la suma y la resta se basa en tres reglas que se probarán en secuencia tomando en cuenta lo siguiente:
- Sólo si una regla fracasa (porque no dispongamos de las cuentas necesarias para completar la operación) procederemos a probar con la siguiente regla.
- La segunda de las reglas solo funciona para los dígitos 1, 2, 3 y 4.
- La tercera regla descompone la operación en otras dos "más simples" : un acarreo a la columna directamente a la izquierda, sea llevar (sumar 1) o tomar prestado (restar 1) de esa columna, más una operación del tipo opuesto (es decir, una resta si estamos sumando o una suma si estamos restando). En este caso:
- La primera operación, con la columna de la izquierda (llevar o tomar prestado), es trivial la mayor parte de las veces, pero no siempre.
- La segunda operación (la opuesta a la inicial) culminará usando las reglas 1 o 2 (nunca 3) de la operación contraria; es decir, la operación acabará aquí.
- Necesitaremos decidir en qué orden haremos estas dos operaciones.
Reglas para la suma
[editar]Estas son las reglas para la suma de un dígito:
| 1 | Trate de añadir las cuentas necesarias |
|---|---|
| 2 | Trate de añadir 5 (una cuenta superior) y retirar el complementario a 5 (cuentas inferiores) |
| 3 | Lleve 1 a la izquierda y reste el complementario a 10 |
Reglas para la resta
[editar]Y estas son las reglas para su sustracción:
| 1 | Trate de retirar las cuentas necesarias |
|---|---|
| 2 | Trate de retirar 5 (cuenta superior) y añadir el complementario a 5 (cuentas inferiores) |
| 3 | Tome prestado 1 de la izquierda y sume el complementario a 10 |
Reglas conjuntas de suma y resta
[editar]Las reglas anteriores para la suma y la resta son de estructura idéntica, por lo que podemos fusionarlas en:
| 1 | Trate de añadir/retirar las cuentas necesarias |
|---|---|
| 2 | Trate de añadir/retirar 5 (cuenta superior) y retirar/añadir el complementario a 5 (cuentas inferiores) |
| 3 | Lleve/tome prestado 1 de la izquierda y reste/sume el complementario a 10 |
¡y así sólo tendremos tres reglas que memorizar! Estas reglas nos ayudarán en la fase inicial de nuestra práctica a decidir qué cuentas hemos de mover, pero con el tiempo las iremos necesitando cada vez menos, conforme vayamos integrando en nuestra memoria motora cada uno de los 180 casos de suma y resta de un dígito y, con la práctica, llegaremos a prescindir totalmente de ellas. Entonces podremos decir que hemos aprendido a sumar y restar con el ábaco.
Las reglas anteriores nos muestran la absoluta simetría de las operaciones de suma y resta con el ábaco y justifican que tratemos ambas operaciones conjuntamente.
Orden de las operaciones
[editar]Antes de pasar a algunos ejemplos preliminares tenemos que decidir qué orden de operación usar en caso de llegar a la regla 3, lo que sucederá la mitad de las veces. Esta regla nos lleva a dividir el problema original en dos partes, con suerte más simples: un acarreo (llevada o préstamo) y una operación del tipo opuesto a la que estamos realizando. ¿Qué hacemos primero?
El método estándar japonés que se enseña actualmente y desde finales del siglo XIX propone realizar primero el préstamo y luego la suma del número complementario en el caso de la resta (lo cual recibe el nombre de sakidama 先珠 en japonés), mientras que en el caso de la suma, la resta del número complementario se hace primero y luego se lleva 1 a la columna de la izquierda (atodama 後珠)[2]. Esto parece inspirado en la estructura de las reglas / versos / rimas chinas utilizadas para enseñar el ábaco desde la antigüedad, pero no parece haber ninguna razón lógica convincente para hacerlo y no todos están de acuerdo.[3].
Como veremos, con el ábaco se trabaja de izquierda a derecha durante la suma y resta de números de varios dígitos, por lo que parece natural intentar respetar este movimiento de izquierda a derecha de la mano sin molestarla con continuas idas y venidas a la columna de la izquierda. Usar siempre sakidama (llevar y tomar prestado primero), tanto para la suma como para la esta, parece lo más natural.
No hace falta decir que si tiene un profesor o un entrenador debe seguir escrupulosamente sus instrucciones, pero si es autodidacta no dude en experimentar hasta encontrar su camino.
Por cierto, en algunos países asiáticos se enseña a usar la mano izquierda para llevar y tomar prestado.
Algunos ejemplos preliminares
[editar]- Ejemplo
- Ponga un 1 en una columna de su ábaco y súmele 3:
- ¿Tenemos a nuestra disposición (inactivas) las cuentas necesarias (3 inferiores) para sumarlas al 1 de nuestro ábaco? ¡Sí!
- * entonces, las activamos y hemos completado la operación con la primera regla.
| A | A | |
|---|---|---|
| Regla 1 | ||
| 1 | 4 |
- Ejemplo
- Entre 3 en una columna de su ábaco y súmele otro 3:
- ¿Tenemos a nuestra disposición (inactivas) las cuentas necesarias (3 inferiores) para sumarlas a las 3 de nuestro ábaco? ¡No!
- * entonces, pasamos a la segunda regla.
- Como el sumando 3 es menor que 5 podemos probar la segunda regla: ¿Tenemos a nuestra disposición (inactiva) una cuenta superior? ¡Sí!
- * entonces, aplicamos la segunda regla: activamos la cuenta superior y retiramos dos cuentas inferiores (el complemento a 5 del sumando 3).
| A | A | |
|---|---|---|
| Regla 2 | ||
| 3 | 6 |
- Ejemplo
- Ponga 9 en una columna de su ábaco y sume 3:
- ¿Tenemos a nuestra disposición (inactivas) las cuentas necesarias (3 inferiores) para sumarlas a las 3 de nuestro ábaco? ¡No!
- * entonces, pasamos a la segunda regla.
- Como el sumando 3 es menor que 5 podemos probar la segunda regla: ¿Tenemos a nuestra disposición (inactiva) una cuenta superior? ¡No!
- * Entonces procedemos a la tercera regla:
- Sume 1 a la columna A y reste 7 (el complemento a 10 de 3) de B
- ¿Tenemos a nuestra disposición (activas, estamos restando ahora de la columna B) las cuentas necesarias (una cuenta superior y 2 inferiores) para retirarlas del 9 de nuestro ábaco? ¡Sí!
- * entonces, retírelas y habremos completado esta parte de la operación con la primera regla.
| A | B | A | B | |
|---|---|---|---|---|
| Regla 3 | ||||
| 0 | 9 | 1 | 2 |
Como puede ver, las reglas utilizadas aquí son las mismas que aparecieron en el Panzhu Suanfa de Xu Xinlu, ¡pero condensadas en sólo tres reglas gracias al concepto de números complementarios!
Veamos ahora los movimientos inversos para la resta:
- Ejemplo
- Ingrese 4 en una columna de su ábaco y reste 3 de la misma:
- ¿Tenemos a nuestra disposición (activas) las cuentas necesarias (3 inferiores) para retirarlas de las 4 en nuestro ábaco? ¡Sí!
- * entonces, las desactivamos y habremos completado la operación con la primera regla.
| A | A | |
|---|---|---|
| Regla 1 | ||
| 4 | 1 |
- Ejemplo
- Entre 6 en una columna de su ábaco y reste 3 de ella:
- ¿Tenemos a nuestra disposición (activas) las cuentas necesarias (3 inferiores) para restarlas a las 6 de nuestro ábaco? ¡No!
- * entonces, pasamos a la segunda regla.
- Como el sustraendo 3 es menor que 5 podemos probar la segunda regla: ¿Tenemos a nuestra disposición (activa) una cuenta superior? ¡Sí!
- * Entonces aplicamos la segunda regla: desactivamos la cuenta superior y agregamos dos cuentas inferiores (el complemento a 5 del sustraendo 3).
| A | A | |
|---|---|---|
| Regla 2 | ||
| 6 | 3 |
- Ejemplo
- Entre 12 en un par de columnas de su ábaco (AB) y reste 3 de B:
- ¿Tenemos a nuestra disposición (activas) las cuentas necesarias (3 inferiores) para retirarlas de B? ¡No!
- * Entonces, intentamos la segunda regla.
- Como el sustraendo 3 es menor que 5 podemos probar la segunda regla: ¿Tenemos a nuestra disposición (activa) una cuenta superior? ¡No!
- * Entonces, pasamos a la tercera regla:
- Tome prestado (reste) 1 de A y sume 7 (el complemento a 10 de 3) a B
- ¿Tenemos a nuestra disposición (inactivas, estamos sumando ahora) Las cuentas necesarias (una cuenta superior y 2 inferiores) para agregarlas a las 2 en B? ¡Sí!
- * entonces, actívelas y habremos completado esta parte de la operación con la primera regla.
| A | B | A | B | |
|---|---|---|---|---|
| Regla 3 | ||||
| 1 | 2 | 0 | 9 |
Tipos de suma y resta de un solo dígito
[editar]La siguiente tabla muestra para cada una de las 180 operaciones elementales de suma y resta qué regla nos resuelve el problema. Puede serle útil durante sus primeras prácticas, para elegir qué dígitos sumar o restar.
| Suma | Resta | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| +1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 3 | -1 | 3 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | |
| +2 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 1 | 3 | 3 | -2 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 1 | |
| +3 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 3 | 3 | 3 | -3 | 3 | 3 | 3 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | |
| +4 | 1 | 2 | 2 | 2 | 2 | 1 | 3 | 3 | 3 | 3 | -4 | 3 | 3 | 3 | 3 | 1 | 2 | 2 | 2 | 2 | 1 | |
| +5 | 1 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | -5 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | |
| +6 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | -6 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | |
| +7 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | -7 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 1 | |
| +8 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | -8 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | |
| +9 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | -9 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | |
Como puede ver, las tablas anteriores para la suma y la resta son imágenes especulares entre sí. Observe también cómo la mitad de los casos corresponden a la regla tres, es decir, requieren acarreos, y de ellos, los marcados en negrita, terminan con una operación de tipo 2 opuesta. Verifique también cómo la regla 2 solo afecta la suma o resta de dígitos menores que 5.
Ejemplos
[editar]Estudie detenidamente los siguientes ejemplos.
- Ejemplo
- Ponga 5 en una columna de su ábaco y sume 7:
En este ejemplo, que requiere un acarreo (regla 3), la resta del número complementario a su vez requiere el uso de la regla 2, que afecta a la cuenta superior.
| A | B | A | B | |
|---|---|---|---|---|
| Regla 3 seguida de regla 2 | ||||
| 0 | 5 | 1 | 2 |
- Ejemplo
- Entre 95 en el ábaco y súmele 7:
Ahora el acarreo conduce a otra operación de tipo 3, que requiere a su vez un nuevo acarreo. En esta operación se ven afectadas tres columnas del ábaco.
| A | B | C | A | B | C | |
|---|---|---|---|---|---|---|
| Regla 3 + regla 3 | ||||||
| 0 | 9 | 5 | 1 | 0 | 2 |
- Ejemplo
- Entre 999995 en el ábaco y súmele 7:
Se trata de una situación extrema, extrapolación del caso anterior, que conviene estudiar detenidamente. ¡El acarreo se extiende o corre a través de las columnas de la izquierda hasta que encuentra un hueco para alojarse!
| A | B | C | D | E | F | G | A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regla 3 + Regla 3 +... | ||||||||||||||
| 0 | 9 | 9 | 9 | 9 | 9 | 5 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
Piense que, si tuviéramos a nuestra disposición una quinta cuenta inferior, como en el caso del ábaco tradicional, podríamos haber evitado este "acarreo" al menos temporalmente.
| A | B | C | D | E | F | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regla 3 | ||||||||||||
| 9 | 9 | 9 | 9 | 9 | 5 | 9 | 9 | 9 | 9 | 10 | 2 |
Para obtener detalles sobre el uso de la quinta bola inferior, puede consultar el capítulo correspondiente una vez que haya adquirido suficiente práctica.
- Ejemplo
- Entre 50 en su ábaco y reste 3:
En este caso de una operación de tipo 3, el acarreo (préstamo) a su vez requiere una operación de tipo 2 (que afecta a la cuenta superior).
| A | B | A | B | |
|---|---|---|---|---|
| ... | ||||
| 5 | 0 | 4 | 7 |
- Ejemplo
- Introduzca 10006 en su ábaco y reste 7:
Finalmente, este es un caso de "pedir prestado" donde tenemos que viajar lejos hacia la izquierda para encontrar algo de lo que poder restar. Estudie también este caso detenidamente.
| A | B | C | D | E | A | B | C | D | ||
|---|---|---|---|---|---|---|---|---|---|---|
| ... | ||||||||||
| 1 | 0 | 0 | 0 | 6 | 0 | 9 | 9 | 9 | 9 |
Se trata también de una situación que se intenta paliar con el uso de una quinta cuenta inferior en los ábacos tradicionales.
Dos consejos
[editar]Hasta aquí nuestras explicaciones teóricas o intelectuales sobre el ábaco. Ahora ya sabe lo que "es" el ábaco oriental y está en camino. Este conocimiento intelectual será su guía durante sus primeros pasos, pero con la práctica, los movimientos de las cuentas se convertirán en una segunda naturaleza para usted y nunca volverá a pensar en todas estas reglas (al menos, hasta que escriba su primer libro sobre el ábaco). Para lograr esto necesitará practicar y practicar y te ofrecemos un par de consejos importantes que le ayudarán a completar el camino que está tomando ahora.
- Nunca lea los resultados intermedios. Este es un mal hábito que no conduce a nada, sólo a perder tiempo y energía mental, y lo que quiere es adquirir rapidez y confort en el uso del ábaco. Su ábaco está ahí para mantener sus números seguros sin que tenga que preocuparse de ellos. Debería limitarse a "reaccionar" a la disposición de las cuentas sin ser consciente del número que estas representan.
- Olvídese de las tablas de sumar y restar, salvo lo que hemos extraído de ellas en forma de números complementarios a 5 y 10. En particular, nunca piense: "Tengo que sumar 7+8, esto da 15, luego tiene que aparecer un quince en el ábaco". Si hace esto, estará "pensando" mientras suma y resta, y eso lo cansará y lo frenará. Si tiene que pensar en algo, piense en las reglas de movimiento de las cuentas y no en los números, ...hasta que sea capaz de sumar y restar mecánicamente mientras piensa en cualquier otra cosa.
Si no sigue estos consejos, probablemente desarrollará un mal hábito que puede ser muy difícil de corregir posteriormente, como ocurre con los malos hábitos que se adquieren, por ejemplo, al estudiar un instrumento musical.
Y ahora la práctica
[editar]Sus primeros ejercicios deben ser lo más simples posible y nada parece más fácil que elegir aleatoriamente dos dígitos, por ejemplo: 6 y 8, y tratar de sumarlos o restarlos (quizás agregando un uno delante del primer número si al restar el segundo necesita tomar prestado). Puede utilizar la tabla de tipos de operaciones explicada anteriormente en este capítulo para conocer de antemano el tipo de operación a realizar.
Posteriormente, se debe proceder a una práctica sistemática de los 180 casos de suma y resta de un solo dígito, para lo cual se propone el siguiente ejercicio que también servirá como introducción a la suma y resta de números de varios dígitos.
Comience con el ábaco en el siguiente estado, con el número 123456789, y agregue el mismo dígito a cada una de las nueve columnas B - J procediendo de izquierda a derecha
| A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Por ejemplo, para sumar 1 a cada uno de los dígito de 123456789; es decir, para sumar 111111111 a 123456798, siga los pasos indicados en la siguiente tabla
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJ | |
| 123456789 | Empezar con esto |
| +1 | Sumar 1 a B (Tipo 1) |
| +1 | Sumar 1 a C (Tipo 1) |
| +1 | Sumar 1 a D (Tipo 1) |
| +1 | Sumar 1 a E (Tipo 1) |
| +1 | Sumar 1 a F (Tipo 1) |
| +1 | Sumar 1 a G (Tipo 1) |
| +1 | Sumar 1 a H (Tipo 1) |
| +1 | Sumar 1 a I (Tipo 1) |
| +1 | Sumar 1 a J (Tipo 3 con doble acarreo) |
| 234567900 | Resultado |
| ABCDEFGHIJ |
y debería llegar al resultado indicado: 123456789 + 111111111 =234567900. La siguiente tabla muestra los resultados de sumar 111111111, 222222222, ... 999999999 a 1234568789.
| d | Resultado |
|---|---|
| 1 | 234567900 |
| 2 | 345679011 |
| 3 | 456790122 |
| 4 | 567901233 |
| 5 | 679012344 |
| 6 | 790123455 |
| 7 | 901234566 |
| 8 | 1012345677 |
| 9 | 1123456788 |
En cuanto a la resta, añadiremos un 1 adicional a la columna A para futuros acarreos:
| A | B | C | D | E | F | G | H | I | K |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y procederemos de forma similar
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJ | |
| 1123456789 | Inicio |
| -1 | Restar 1 de B (Tipo 1) |
| -1 | Restar 1 de C (Tipo 1) |
| -1 | Restar 1 de D (Tipo 1) |
| -1 | Restar 1 de E (Tipo 1) |
| -1 | Restar 1 de F (Tipo 2) |
| -1 | Restar 1 de G (Tipo 1) |
| -1 | Restar 1 de H (Tipo 1) |
| -1 | Restar 1 de I (Tipo 1) |
| -1 | Restar 1 de J (Tipo 3) |
| 1012345678 | Resultado |
| ABCDEFGHIJ |
y deberiamos obtener: 1012345678 = 1123456789-111111111. Para el resto de dígitos, la siguiente tabla muestra los resultados de restar 111111111, 222222222, ... 999999999 de 1123456789.
| d | Resultado |
|---|---|
| 1 | 1012345678 |
| 2 | 901234567 |
| 3 | 790123456 |
| 4 | 679012345 |
| 5 | 567901234 |
| 6 | 456790123 |
| 7 | 345679012 |
| 8 | 234567901 |
| 9 | 123456790 |
Durante un tiempo debería practicar estos ejercicios a diario hasta que note que poco a poco va sustituyendo su trabajo intelectual (pensando en las reglas a utilizar) por una respuesta mecánica instintiva.
Sumas y restas de varios dígitos
[editar]Trabajar siempre de izquierda a derecha
[editar]En castellano, los números se nombran comenzando con la potencia más alta de diez; 327 es "trescientos veintisiete" y no "siete veinte trescientos". Este es el caso de muchos otros idiomas, incluidos el chino y el japonés, pero no de otros como los de la familia semítica. Esta es la razón principal por la que en el ábaco la suma o resta de números de varios dígitos se trabaja de izquierda a derecha; esto hará las cosas más sencillas, tanto si tenemos que leer los números de una lista como si alguien nos los dicta.
Por ejemplo, obtengamos 44 + 78. Comencemos con un ábaco puesto a cero e introduzcamos el primer sumando 44 en cualquier lugar del mismo (alineado con una marca de varilla unitaria si lo desea, esto es conveniente pero no esencial)
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
ponga 4 (40) en B
| A | B | C |
|---|---|---|
| 0 | 4 | 0 |
ahora 4 en C
| A | B | C |
|---|---|---|
| 0 | 4 | 4 |
ahora sume 7 (70) a B
| A | B | C |
|---|---|---|
| 1 | 1 | 4 |
por último sume 8 a C
| A | B | C |
|---|---|---|
| 1 | 2 | 2 |
El resultado: 122 aparece en ABC.
En una forma más compacta:
| Abacus | Comment |
|---|---|
| ABC | |
| . | Marca unidad en C |
| 4 | Entre 4 en B (40) |
| 44 | Entre 4 en C |
| +7 | Sume 7 a B (70) |
| 114 | |
| +8 | Sume 8 a C |
| 122 | Resultado |
| . | Marca unidad en C |
Otro ejemplo. Supongamos que tenemos que obtener el total de estas cantidades en euros:
| 7.77 € |
| 11.99 € |
| 69.62 € |
| 54.43 € |
| -96.99 € |
| Total |
|---|
| 46.82 € |
Comience poniendo a cero su ábaco e introduzca el primer número (de izquierda a derecha). Puede alinearlo con algunos de los marcadores de puntos unitarios si lo desea.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 0 | 7 | 7 | 7 | 0 |
| Ábaco | Comentario |
|---|---|
| ABCDEF | |
| . . | Marca unidad |
| 777 | Entre 7.77 € |
| +1 | Sumar 11.99 € |
| +1 | |
| +9 | |
| +9 | |
| 1976 | Resultado intermedio |
| +6 | Sumar 69.62 € |
| +9 | |
| +6 | |
| +2 | |
| 8938 | Resultado intermedio |
| +5 | Sumar 54.43 € |
| +4 | |
| +4 | |
| +3 | |
| 14381 | Resultado intermedio |
| -9 | Restar 96.99 # |
| -6 | |
| -9 | |
| -9 | |
| 4682 | Total: 46.82 € |
| . . | Marca unidad |
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 4 | 6 | 8 | 2 | 0 |
Formas de practicar la suma y la resta
[editar]Con hojas de ejercicios
[editar]Debería comenzar su práctica sumando y restando series cortas de números enteros pequeños; por ejemplo, de 3 a 5 números de 2 o 3 dígitos. Por ejemplo:
| 594
807 -660 -466 275 |
880
343 -181 -580 462 |
480
879 -472 19 906 |
336
309 450 -335 760 |
480
-269 -122 780 869 |
963
744 -154 -811 742 |
29
261 909 186 1385 |
373
-163 423 -445 188 |
Aumente progresivamente el tamaño de estas series hasta llegar a 10 números y, a partir de aquí, aumente progresivamente el tamaño de los números a sumar / restar a 5 o 6 dígitos. Por ejemplo:
| 514299
127127 774517 -895449 907858 67913 -918061 930513 -582082 -722266 204369 |
375287
611780 -312229 618415 -78719 -467463 -406146 481087 958663 216295 1996970 |
351129
806691 600755 -368489 815758 573731 51556 668536 -609796 713031 3602902 |
882678
876701 -365479 -157706 17497 999762 -262868 -910991 -56430 -333692 689472 |
758320
769094 991286 -49973 74914 -590317 644711 -900673 -449638 -380293 867431 |
562337
315480 -540643 513724 -651332 359925 285750 883744 -591941 75119 1212163 |
388730
-287030 -11891 323483 212117 373242 118641 -693301 442672 -370874 495789 |
798306
-483827 572862 840450 452414 -298427 503089 175358 918199 315118 3793542 |
Por lo tanto, necesitará colecciones de problemas de este tipo que puede generar con algunas utilidades gratuitas en Internet[4] [5] [6].
Con este tipo de práctica desarrollarás dos habilidades diferentes
- Sumar y restar eficientemente con el ábaco.
- leer números de un vistazo y guardarlos en la memoria el tiempo suficiente para trabajarlos en el ábaco.
Esto último es fundamental para, por ejemplo, hacer uso del ábaco en contabilidad.
Sin hojas de ejercicios
[editar]El ejercicio 123456789
[editar]En los libros antiguos sobre el ábaco era común demostrar la suma y la resta mediante un conocido ejercicio que consiste en sumar el número 123456789 nueve veces a un ábaco puesto a cero hasta llegar al número 1111111101, y luego borrarlo nuevamente restando el mismo número otras nueve veces. Este es un ejercicio conveniente porque usa muchos de los 180 casos de suma y resta de 1 dígito (pero no todos) y permite practicar la suma y resta con el ábaco solo, sin hojas de ejercicios en papel, pero no es un ejercicio elemental dada su longitud. Necesitará, por lo tanto, algo de tiempo de práctica para completarlo sin errores.
A lo largo de este ejercicio se obtienen los siguientes resultados parciales:
| 000000000 |
| 123456789 |
| 246913578 |
| 370370367 |
| 493827156 |
| 617283945 |
| 740740734 |
| 864197523 |
| 987654312 |
| 1111111101 |
Para más detalles, consulte el capítulo: Variantes del Ejercicio 123456789.
Sumas y restas con otros ábacos
[editar]Todo lo que aprenda sobre el ábaco oriental funcionará bien con otros tipos de ábaco o al menos simplificará su aprendizaje. Recuerde que las operaciones básicas del ábaco son la suma y la resta y todo lo demás debe reducirse a una secuencia de estas dos operaciones y al problema de cómo organizar tal secuencia de operaciones en el ábaco.
Varillas de cálculo
[editar]Las varillas de cálculo son otro ejemplo de un ábaco bi-quinario, por lo que se aplican las mismas tres reglas de suma y resta estudiadas aquí. Solo tiene que tener en cuenta que los conceptos de activar/desactivar cuentas se traducen en colocar/retirar varillas de la mesa y que "tener a nuestra disposición" varillas para añadir no se refiere al montón de varillas listas para usar que tenemos en la caja, sino a "encajar" dentro de los límites de representación de los números (una varillas de valor 5 y 5 varillas de valor 1 como máximo).
Ábaco ruso
[editar]El ábaco ruso (Schoty) no es un ábaco bi-quinario; por lo que la segunda de las reglas de suma y resta que se dan aquí no funciona. todo se resuelve con la ayuda de la primera y la tercera reglas exclusivamente.
Recursos externos
[editar]- Uitti, Stephen. «Soroban Sheets (Addition and subtraction)». Soroban.
- Uitti, Stephen. «Soroban Sheets (Multiplication)». Soroban.
- «The generator». Practicing the soroban.
Referencias
[editar]- ↑ Xú Xīnlǔ (徐心魯) (1993) [1573] (en Chino). Pánzhū Suànfǎ (盤珠算法). Zhōngguó kēxué jìshù diǎnjí tōng huì (中國科學技術典籍通彙).
- ↑ Kojima Takashi (1954). The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle Co., Inc.. ISBN 978-0-8048-0278-9. https://archive.org/details/japaneseabacus00taka.
- ↑ Abraham, Ralph (2011). «Smart Moves». The Soroban Site of the Visual Math Institute. Archivado desde el original, el 18 de Enero de 2020. Consultado el 20 de Septiembre de 2021.
- ↑ Uitti, Stephen. «Soroban Sheets (Addition and subtraction)». Soroban.
- ↑ Uitti, Stephen. «Soroban Sheets (Multiplication)». Soroban.
- ↑ «The generator». Practicing the soroban.
Multiplicación Moderna
[editar]|
Debería lograr algunas habilidades básicas de suma y resta antes de intentar la multiplicación. |
Introducción
[editar]El concepto básico de multiplicación de números naturales es el de una suma repetida.
Por ejemplo, para multiplicar 47 por 23 solo es necesario sumar 23 47 veces o sumar 47 23 veces; lo podemos hacer con nuestro ábaco:
| Ábaco | Comentario |
|---|---|
| ABCDEFHIJ | |
| . . . | Marcas de unidad |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 1 47 | |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 2 94 | |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 3 141 | |
| ... | Continuar del mismo modo
19 veces...! |
| 22 1034 | |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 23 1081 | Fin. 23×47=1081 |
| . . . | Marcas de unidad |
Donde repetimos 23 veces la suma de 47 a las columnas IJ mientras sumamos 1 a C para tener un "contador" a nuestra disposición. ¡Pero esto es tremendamente lento! Una forma más eficiente de hacer lo mismo puede ser la siguiente:

| Ábaco | Comentario |
|---|---|
| ABCDEFHIJ | |
| . . . | Marcas unidad |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 1 47 | |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 2 94 | |
| +1 +47 | Sumar 1 a C y 47 a IJ |
| 3 141 | |
| +1 +47 | Sumar 1 a B y 47 a HI |
| 13 511 | |
| +1 +47 | Sumar 1 a B y 47 a HI |
| 23 1081 | Fin. 23×47=1081 |
| . . . | Marcas unidad |
Donde esta vez, después de agregar 47 tres veces a IJ (y 1 a C), nos hemos desplazado una columna a la izquierda y hemos comenzado a agregar 47 a las columnas HI (y 1 a B). Sumar 47 en HI equivale a sumar 470 = 10 × 47 a HIJ (10 a BC) reduciendo drásticamente el número de operaciones a realizar, porque después de hacerlo solo dos veces llegamos a 23 en el contador BC y 1081 en GHIJ, el resultado final. Esta forma de multiplicar fue la habitual en las calculadoras mecánicas que aparecieron a finales del siglo XIX y que se siguieron utilizando hasta la década de los 70. Pero esto sigue siendo excesivamente lento.
Piense que el ábaco tal como lo conocemos ahora permite sumar muy rápido, pero que antes de su invención se usaban varillas de cálculo que son extraordinariamente lentas de manejar. Por lo tanto, no es sorprendente que los matemáticos chinos, buscando abreviar los cálculos, finalmente inventaran la tabla de multiplicar decimal, tal como la conocemos nosotros, unos siglos antes de nuestra era.
La tabla de multiplicar
[editar]
Esta es la tabla de multiplicar decimal como la aprendemos en la escuela:
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Pero viviendo en la era de las computadoras, lo más probable es que pronto comencemos a usar una calculadora electrónica y en la edad adulta hagamos pocas multiplicaciones a mano. A menudo, muchos de nosotros, incluso los matemáticos, no tenemos la tabla de multiplicar "fresca" en la memoria y esto puede ser una mala noticia para quien se inicia: si se quiere multiplicar (y dividir) de manera eficiente con un ábaco, es necesario "refrescar" la tabla de multiplicar en la memoria y esto puede requerir un cierto tiempo de práctica.
Usando la tabla de multiplicar podemos resolver el problema de multiplicación en la forma:
es decir, solo tenemos que recuperar los productos parciales: de la tabla de multiplicar y sumarlos en los lugares correctos, como hacemos con papel y lápiz
47 ×23 ----- 21 12 (×10) 14 (×10) + 8 (×100) ----- 1081
Esto es absolutamente paralelo al método de multiplicación que vamos a seguir con el ábaco.
El método de multiplicación moderno
[editar]Cuando multiplicamos dos números y , llamamos a ambos números factores y producto al resultado , pero también es común llamar multiplicando a uno de los factores y multiplicador al otro. Sin embargo, a la hora de multiplicar con el ábaco:
- Multiplicando
- Es el factor que vamos a manipular sobre el ábaco y que nos guiará para obtener los productos parciales de forma ordenada y alinearlos correctamente para su suma en las posiciones correctas.
- Multiplicador
- Es el factor que no vamos a manipular sobre el ábaco. de hecho no es obligatorio ni siquiera ingresarlo (pero es conveniente). Por lo general, será el factor con menos dígitos de los dos.
Disposición de multiplicación
[editar]Hay dos formas de introducir ambos factores en el ábaco que pueden considerarse prácticamente equivalentes; Cada uno de ellos tiene sus propias ventajas y desventajas. Lo mismo puede decirse de la división que estudiaremos en el próximo capítulo. Siéntase libre de experimentar con ambos arreglos.
Disposición china tradicional
[editar]El multiplicando se pone a la izquierda en el ábaco y el multiplicador lo suficientemente alejado del mismo. Al menos tantas columnas como dígitos tenga el multiplicador más dos, o mejor tres, deben dejarse libres a la derecha del multiplicando.
- Ejemplo
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 |
o en forma de tabla:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 345 67 |
Disposición tradicional japonesa
[editar]Esta es la forma inversa. El multiplicador se sitúa a la izquierda y el multiplicando a la derecha, dejando al menos dos columnas vacías en el medio. Necesitamos tener al menos tantas columnas libres a la derecha del multiplicador como el número de dígitos del multiplicador más uno.
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 7 | 3 | 4 | 5 |
o en forma de tabla:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 67 345 |
Esta es la forma que ha sido más popular en Japón.[1] y terminó siendo importada también a China. También es la disposición que usaremos en este capítulo.
Multiplicación de 1 dígito × 1 dígito
[editar]Por supuesto, esto es tan trivial que no necesitamos un ábaco, pero sirve para introducir el resto de ejemplos. Supongamos que tenemos que multiplicar, tomemos 7 como multiplicador, 8 como multiplicando y adoptemos disposición japonesa que acabamos de explicar; es decir, partimos de:
| A | B | C | D | E | F | G | ||
|---|---|---|---|---|---|---|---|---|
| 7 | 8 |
y procedamos del siguiente modo:
| Ábaco | Comentario |
|---|---|
| ABCDEFG | |
| 7 8 | Planteando el problema |
| +56 | Multiplicar D×A y sumarlo a EF |
| 7 856 | |
| 7 |
Borrar D |
| 7 56 | Resultado: 7×8=56 en EF |
| A | B | C | D | E | F | G | ||
|---|---|---|---|---|---|---|---|---|
| 7 | 5 | 6 |
Sí, tiene razón; es usted quien hizo la multiplicación, no el ábaco. En el siguiente ejemplo sin embargo, el ábaco comienza a mostrar su utilidad.
Multiplicación de 1 dígito × 2 dígitos
[editar]Multipliquemos: , el multiplicando será 83.
| A | B | C | D | E | F | G | H | ||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 8 | 3 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGH | |
| 7 83 | Planteo |
| +21 | Multiplicar E × A y sumarlo a FG |
| 7 8321 | |
| 7 8 |
Borrar E |
| 7 8 21 | |
| +56 | Multiplicar D × A y sumarlo a EF |
| 7 8581 | |
| 7 |
Borrar D |
| 7 581 | Resultado: 7×83=581 |
| A | B | C | D | E | F | G | H | ||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 5 | 8 | 1 |
Al menos, el ábaco ha servido para sumar los dos productos parciales enFG y EF.
Multiplicación de 2 dígitos × 2 dígitos
[editar]Ahora multipliquemos .
| A | B | C | D | E | F | G | H | I | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 8 | 3 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 79 83 | Planteo |
| +21 | Multiplicar F×A y sumarlo a GH |
| +27 | Multiplicar F×B y sumarlo a HI |
| 79 83237 | |
| 79 8 |
Borrar F |
| 79 8 237 | |
| +56 | Multiplicar E×A y sumarlo a FG |
| +72 | Multiplicar E×B y sumarlo a GH |
| 79 86557 | |
| 79 |
Borrar E |
| 79 6557 | Resultado: 79×83=6557 en FGHI |
| A | B | C | D | E | F | G | H | I | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 6 | 5 | 5 | 7 |
Multiplicación de varios dígitos
[editar]Generalizando lo visto en los ejemplos anteriores:
- Para cada dígito del multiplicando, comenzando por la derecha
-
- Multiplicar el dígito actual del multiplicando por los dígitos del multiplicador (de izquierda a derecha), sumando el primer producto parcial a las dos columnas a la derecha del dígito actual del multiplicando, y el resto de los productos desplazandonos sucesivamente una columna a la derecha cada vez.
- Borrar el dígito multiplicando actual.
Veámoslo con el siguiente ejemplo: :
| A | B | C | D | E | F | G | H | I | K | J | L | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 9 | 8 | 3 | 5 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKL | |
| 799 835 | Planteamiento |
| +35 | Multiplicar H×A y sumarlo a IJ |
| +45 | Multiplicar H×B y sumarlo a JK |
| +45 | Multiplicar H×C y sumarlo a KL |
| 799 8353995 | |
| 799 83 |
Borrar H |
| 799 83 3995 | |
| +21 | Multiplicar G×A y sumarlo a HI |
| +27 | Multiplicar G×B y sumarlo a IJ |
| +27 | Multiplicar G×C y sumarlo a JK |
| 799 8327965 | |
| 799 8 |
Borrar G |
| 799 8 27965 | |
| +56 | Multiplicar F×A y sumarlo a GH |
| +72 | Multiplicar F×B y sumarlo a HI |
| +72 | Multiplicar F×C y sumarlo a IJ |
| 799 8667165 | |
| 799 |
Borrar F |
| 799 667165 | Resultado: 799×835=667165 |
| A | B | C | D | E | F | G | H | I | K | J | L | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 9 | 6 | 5 | 7 | 1 | 6 | 5 |
Ceros embebidos
[editar]Sea particularmente cuidadoso cuando alguno de los factores tiene ceros internos; por ejemplo:
| A | B | C | D | E | F | G | H | I | K | J | L | M | N | O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 0 | 7 | 5 | 2 | 7 | 0 | 7 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLMNO | |
| 3075 2707 | Planteamiento |
| +21 | Multiplicar JxA, y sumarlo a KL |
| +49 | Multiplicar JxC, y sumarlo a MN! |
| +35 | Multiplicar JxD, y sumarlo a NO |
| 3075 270721525 | |
| 3075 270 |
Borrar J |
| 3075 27 21525 | |
| +21 | Multiplicar HxA, y sumarlo a IJ |
| +49 | Multiplicar HxC, y sumarlo a KL! |
| +35 | Multiplicar HxD, y sumarlo a LM |
| 3075 2 |
|
| 3075 272174025 | Borrar H |
| 3075 2 2174025 | |
| +06 | Multiplicar GxA, y sumarlo a HI |
| +14 | Multiplicar GxC, y sumarlo a JK! |
| +10 | Multiplicar GxD, y sumarlo a KL |
| 3075 2 8324025 | |
| 3075 |
Borrar G |
| 3075 8324025 | Resultado: 3075×2707=8324025 |
| A | B | C | D | E | F | G | H | I | K | J | L | M | N | O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 0 | 7 | 5 | 8 | 3 | 2 | 4 | 0 | 2 | 5 |
La columna de la unidad y los decimales
[editar]Por favor, revise todos los ejemplos vistos hasta ahora y compruebe que, en todos los casos:
|
La columna de las unidades del producto se ubica columnas a la derecha de la columna de la unidades del multiplicando; donde es el número de dígitos del multiplicador. |
Esta es una regla general para la multiplicación de números naturales siguiendo el método moderno de multiplicación que estamos estudiando. Es conveniente tener en cuenta esta regla ya que el producto podría tener ceros al final, como en el caso ; lo que podría confundirle. Por ejemplo:
| A | B | C | D | E | F | G | H | I | K | J | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 1 | 6 | 2 | 5u |
En el diagrama anterior, la barra unitaria del multiplicando es la columna H (señalada con un punto blanco en la barra). Después de la multiplicación, el ábaco muestra:
| A | B | C | D | E | F | G | H | I | K | J | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 5 | 2 | 0 | 0 | 0u |
Necesita saber que la barra unitaria del resultado es varillas a la derecha de H (es decir, en J) para leer correctamente el resultado 52000.
Podemos extender esta regla a números decimales :
|
La columna de las unidades del producto se encuentra columnas a la derecha de la columna de las unidades del multiplicando; donde es el número de dígitos del multiplicador a la izquierda de su punto decimal (¡que podría ser negativo!). |
La siguiente tabla muestra los valores para algunos multiplicadores:
| Multiplicadores | n |
|---|---|
| 32.7 | 2 |
| 3.27 | 1 |
| 0.327 | 0 |
| 0.00327 | -2 |
Multipliquemos ; La varilla de las unidades es F.
| A | B | C | D | E | F | G | H | I | K | J | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 1 | 6 | 2 | 5 |
y para el multiplicador , tenemos
| A | B | C | D | E | F | G | H | I | K | J | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 0 | 0 | 5 | 2 |
de modo que la barra unitaria del producto es barras a la derecha de F, es decir, una barra a su izquierda ( E ) y el resultado debe leerse como .
Referencias
[editar]- ↑ The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle Co., Inc.. 1954. ISBN 978-0-8048-0278-9. https://archive.org/details/japaneseabacus00taka.
Recursos externos
[editar]Hojas de ejercicios
- Uitti, Stephen. «Soroban Sheets (Multiplication)». Soroban.
- «The generator». Practicing the soroban.
Otras lecturas
[editar]- «Multiplication». The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle Co., Inc.. 1954. ISBN 978-0-8048-0278-9. https://archive.org/details/japaneseabacus00taka/page/52/mode/2up.
- Heffelfinger, Totton (2004). «Multiplication». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el June 29, 2021.
División Moderna
[editar]Introducción y primeros métodos
[editar]División euclidiana
[editar]Si consideramos dos números naturales y , la división de por (indicado como o ) responde a la pregunta de cuántas veces el número está contenido en el número . El número en es el dividendo y el divisor. La respuesta o resultado se denomina cociente.
Tomemos y como ejemplo. No hay forma más sencilla de proceder para responder a la pregunta que mediante la resta repetida, contando el número de veces que podemos restar el divisor del dividendo. Podemos hacerlo directamente sobre el ábaco usando una columna como contador:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKL | |
| 35 1225 | |
| +1 -35 | Restar 35 de KL, sumar 1 al contador en F |
| 35 1 1190 | |
| +1 -35 | Restar 35 de KL, sumar 1 al contador en F |
| 35 2 1155 | |
| +1 -35 | Restar 35 de KL, sumar 1 al contador en F |
| 35 3 1120 | |
| ... | Continuar 33 veces mas del mismo modo... |
| 35 33 70 | |
| +1 -35 | Restar 35 de KL, sumar 1 al contador en F |
| 35 34 35 | |
| +1 -35 | Restar 35 de KL, sumar 1 al contador en F |
| 35 35 00 | Hecho!, el cociente es 35 en EF |
Así descubrimos que el número está contenido exactamente veces en , ya que no podemos continuar restando sin empezar a tratar con números negativos. Por lo tanto, en este ejemplo, el cociente es: .
Como podemos ver, en este caso podemos escribir , o bien:
lo que no podemos esperar en el caso general. Si repitiéramos el proceso con , veríamos que después de restar por nos quedaría en el ábaco, del que no podríamos seguir restando sin introducir números negativos. Por lo tanto, tenemos que ; es decir, el resultado de dividir por da un cociente de dejando un resto de . En general tendremos:
dónde:
- : dividendo
- : divisor
- : cociente
- : resto
En el caso de que el resto sea cero, decimos que la división es exacta y el dividendo es un múltiplo del divisor.
Este es el concepto de división euclidiana para números naturales a la que se puede reducir la división de números con fracciones decimales sin más que multiplicar y/o por potencias de 10 adecuadas y después ajustar el punto decimal en el resultado.
Algunas mejoras: métodos de división a trozos
[editar]El procedimiento seguido en la sección anterior es el más simple posible conceptualmente, pero es extraordinariamente largo e ineficiente. En lugar de comenzar directamente restando el divisor () del dividendo, comencemos preguntando qué potencia de 10 veces el divisor podemos restar del dividendo; en nuestro caso: ¿podemos restar 3500, 350 o solo 35? Claramente podemos restar 350 y comenzaremos a restar trozos de 350 , y cuando no podamos continuar, comenzaremos a restar trozos de 35 de la siguiente manera:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Comienzo, contador en D |
| 35 1 875 | Restar 35 de GH, sumar 1 al contador D |
| 35 2 525 | Restar 35 de GH, sumar 1 al contador D |
| 35 3 175 | Restar 35 de GH, sumar 1 al contador D |
| 35 31140 | Restar 35 de HI, sumar 1 al contador E |
| 35 32105 | Restar 35 de HI, sumar 1 al contador E |
| 35 33 70 | Restar 35 de HI, sumar 1 al contador E |
| 35 34 35 | Restar 35 de HI, sumar 1 al contador E |
| 35 35 00 | Restar 35 de HI, sumar 1 al contador E |
| 35 35 | Sin resto, hecho!. El cociente es 35 |
Lo cual ha sido mucho más rápido. Como ve en el proceso anterior, hemos reducido intencionadamente la distancia entre el contador y el dividendo tanto como nos ha sido posible. Esto quizás oscurezca un poco el proceso, pero nos acerca a lo que haremos habitualmente con el método de división moderno que explicamos más abajo. Estudie el cálculo anterior cuidadosamente usando su propio ábaco. El método de división que hemos seguido aquí es el usado por las calculadoras mecánicas que mencionamos en el capítulo dedicado a la multiplicación.
Continuemos desde aquí buscando aún más eficiencia.
Si podemos duplicar fácilmente el divisor y retenerlo en la memoria, podemos acortar la operación restando trozos de una o dos veces el divisor.
| Veces | Trozo |
|---|---|
| 1 | 35 |
| 2 | 70 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Comienzo, contador en D |
| 35 2 525 | Restar 70 de GH, sumar 2 al contador en D |
| 35 3 175 | Restar 35 de GH, sumar 1 al contador en D |
| 35 32105 | Restar 70 de HI, sumar 2 al contador en E |
| 35 34 35 | Restar 70 de HI, sumar 2 al contador en E |
| 35 35 00 | Restar 35 de HI, sumar 1 al contador en E |
| 35 35 | Sin resto. Hecho, El cociente es 35 |
O incluso mejor si podemos construir una tabla como la de abajo doblando el divisor tres veces[1]:
| Veces | Trozo |
|---|---|
| 1 | 35 |
| 2 | 70 |
| 4 | 140 |
| 8 | 280 |
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Comienzo, contador en D |
| 35 2 525 | Restar 70 de GH, sumar 2 al contador en D |
| 35 3 175 | Restar 35 de GH, sumar 1 al contador en D |
| 35 34 35 | Restar 140 de HI, sumar 4 al contador en E |
| 35 35 00 | Restar 35 de HI, sumar 1 al contador en E |
| 35 35 | Sin resto. Hecho, El cociente es 35 |
que es algo más corto y, claramente, nada podría ser más rápido que tener una tabla de multiplicar completa del divisor.
Tabla de multiplicación del divisor
[editar]Si disponemos de la tabla de múltiplos del divisor, en nuestro caso 35
| Veces | Trozo |
|---|---|
| 1 | 35 |
| 2 | 70 |
| 3 | 105 |
| 4 | 140 |
| 5 | 175 |
| 6 | 210 |
| 7 | 245 |
| 8 | 280 |
| 9 | 315 |
entonces podemos abreviar las cosas aún más.
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 35 1225 | Comienzo, contador en D |
| 35 3 175 | Restar 105 de GH, sumar 3 al contador en D |
| 35 35 00 | Restar 175 de HI, sumar 5 al contador en E |
| 35 35 | Resto nulo. Hecho, el cociente es 35 |
No hay duda, este es un método de división óptimo, ya que nada puede ser más rápido y cómodo... una vez que tengamos una tabla como la de arriba. Pero calcular la tabla de multiplicar de un divisor lleva tiempo, requiere papel y lápiz para anotarla y este trabajo adicional sólo estaría justificado si tenemos una gran cantidad de divisiones por hacer con el mismo divisor común.
En 1617 John Napier (Neper), el padre de los logaritmos, presentó un invento para aliviar este problema que consiste en una serie de tablillas, conocidas como ábaco neperiano o tablas neperianas, con la tabla de multiplicar de un dígito escrita en ellos y que podían combinarse para obtener la tabla de multiplicar de cualquier número. Por ejemplo, en nuestro caso

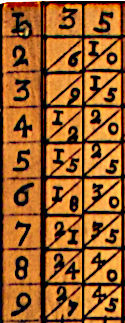
|
1 | 35 |
| 2 | 70 | |
| 3 | 105 | |
| 4 | 140 | |
| 5 | 175 | |
| 6 | 210 | |
| 7 | 245 | |
| 8 | 280 | |
| 9 | 315 |
No hay duda de que tal invento se extendió muy pronto a Oriente de mano de los misioneros Jesuitas[2] y se usó junto con el ábaco, pero este uso debe considerarse excepcional; no todo el mundo tenía tablillas neperianas al alcance de la mano. Se necesita otra herramienta y esa herramienta es la tradicional tabla de multiplicar de 1 dígito que se aprende de memoria y que vamos a usar como aproximación a la tabla de multiplicar específica del divisor (la que se usó arriba), esta tabla nos guiará para elegir el dígito del cociente que debemos probar.
Cabe señalar que los procedimientos anteriores no agotan las posibilidades de los métodos de división por trozos[3].
División moderna
[editar]División moderna vs tradicional
[editar]El método moderno de división se llama así porque, a lo largo de la primera mitad del siglo XX, su uso ha desplazado al del método tradicional, pero de hecho es mucho más antiguo que éste, habiendo sido desplazado por él en el siglo XIII. Una característica del método moderno es el uso de la tabla de multiplicar de 1 dígito como guía para la elección de la cifra provisional que tenemos que probar como cociente y para el cálculo del trozo que tenemos que restar del dividendo.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
En comparación, el método tradicional utiliza tanto una tabla de división especial como guía para la cifra provisional del cociente como la tabla de multiplicar para calcular la parte a sustraer.
La razón principal por la que el método moderno comenzó a desplazar al método tradicional en Japón, después de la Restauración Meiji, es que puede ser aprendido de manera más fácil y rápida por quienes ya saben dividir con papel y lápiz al no requerir la memorización de una compleja tabla de división. Por otro lado, anticipemos que el método tradicional hace de la división un proceso completamente automatizado, sin necesidad de pensar; solo hay que seguir las reglas para obtener el resultado, lo que permite realizar la operación sin ningún cansancio mental. Trataremos sobre esta división tradicional el la sección de este libro dedicada a los métodos tradicionales.
Punto clave de la división con el ábaco
[editar]Uno de los puntos clave del aprendizaje del ábaco es ser conscientes de que este instrumento nos permite corregir algunas cosas de forma muy rápida y sin dejar rastros, lo que convierte al ábaco en un instrumento especialmente indicado para procedimientos de prueba y error. Esto nos es especialmente útil en el caso de la división. Si tenemos que dividir , en lugar de forzar nuestra mente tratando de encontrar la cifra correcta del cociente, simplemente elegimos una cifra aproximada provisional o interina simplificando el problema original a y la probamos intentando restar el trozo (cociente provisional)✕79283 del dividendo; al hacerlo, ocurrirá una de las siguientes situaciones:
- El dígito del cociente intermedio es correcto
- es decir, podemos restar el fragmento (dígito del cociente intermedio) ✕ (divisor), pero no podemos restar el cociente una vez más porque el resto es menor que el divisor.
- Es insuficiente y debemos revisarlo al alza
- podemos restar el fragmento (dígito intermedio del cociente) ✕ (divisor), pero aún podemos restar el cociente una vez más porque el resto es mayor o igual que el divisor. Agregamos uno al cociente intermedio y restamos el divisor nuevamente del resto.
- Es excesivo y debemos revisarlo a la baja.
- esta es la situación más compleja y propensa a errores. Por lo general, descubrimos demasiado tarde (en medio de la resta de fragmentos) que la cifra intermedia es excesiva y tenemos que retroceder, restar uno del cociente y restaurar el dividendo/resto agregándole lo que se le ha restado en exceso antes de que podamos seguir.
Por tanto, el proceso de obtención de un dígito del cociente tiene dos fases (prueba y error):
- Elegir un dígito de cociente provisional.
- Probar si es correcto y modificarlo si no lo es.
Una vez que hayamos encontrado la cifra correcta, generalmente tendremos un resto distinto de cero que actuará como dividendo si queremos extender la división al siguiente dígito del cociente.
Veremos todo esto a lo largo de los ejemplos que siguen, pero primero, necesitamos algunas palabras sobre cómo organizar la división en el ábaco.
Disposición en el ábaco de la división moderna
[editar]El dividendo es el término activo con el que vamos a trabajar en el ábaco, el divisor es inactivo y permanecerá invariable durante la operación, de hecho no es imprescindible introducirlo en el ábaco pero sí recomendable, especialmente para los principiantes. Como en el caso de la multiplicación, existen dos estilos para colocar dividendo y divisor en el ábaco, cada uno con sus ventajas y desventajas. Siéntase libre de probar ambas formas.
Disposición tradicional china
[editar]El divisor se sitúa en el extremo derecho del ábaco mientras que el dividendo se coloca hacia la izquierda, dejando al menos dos columnas libres a su izquierda.
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 5 | 3 | 5 |
Disposición tradicional japonesa
[editar]El divisor va al extremo izquierdo del ábaco mientras que el dividendo se sitúa a su derecha, dejando al menos cuatro columnas libres entre los dos términos.
| A | B | C | D | E | F | G | H | I | K | J | L | M | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 1 | 2 | 2 | 5 |
En este capítulo usaremos el estilo japonés para los ejemplos, pero siéntase libre de probar ambos.
Colocando la cifra del cociente
[editar]La cifra del cociente intermedio se coloca en una de las dos columnas directamente a la izquierda del dividendo. Para decidir en cuál, necesitamos comparar el divisor con un número igual de cifras de los primeros dígitos del dividendo, agregando ceros a su derecha si fuera necesario; llamemos a estas cifras el dividendo de trabajo:
- Dividendo de trabajo mayor o igual que el divisor
- esto significa que el divisor cabe en el dividendo de trabajo y el cociente, es decir, el número de veces que el divisor entra en el dividendo de trabajo, se sitúa en la segunda columna a la izquierda del primer dígito del dividendo
- Ejemplo: 827÷46. El dividendo de trabajo 82 es mayor que el divisor 46, luego el cociente intermedio va a la segunda columna a la izquierda del dividendo. La tabla de multiplicar sugiere que usemos 2 como cociente provisional (simplificando 827÷46 a 8÷4)
827÷46 Ábaco Comentario ABCDEFGHIJKLM 46 827 46 2 827 Situamos el cociente provisional 2 en E
- Dividendo de trabajo menor que el divisor
- esto significa que el divisor no cabe en el dividendo de trabajo. En este caso, necesitamos incluir el siguiente dígito del dividendo, o un cero si no quedan más, en nuestro dividendo de trabajo, y el cociente, el número de veces que el divisor entra en este dividendo de trabajo ampliado, se sitúa en la columna directamente a la izquierda del primer dígito del dividendo
- Ejemplo: 18÷467, el dividendo de trabajo 180 es menor que 467, entonces lo ampliamos a 1800 y el cociente provisional se situará en la primera columna a la izquierda del dividendo. La tabla de multiplicar sugiere que usemos 4 como cociente intermedio después de simplificar 1800÷467 a 18÷4.
Caption text Ábaco Comentario ABCDEFGHIJKLM 467 18 467 418 Situamos el cociente provisional 4 en G
Ejemplos
[editar]Debe comenzar haciendo ejercicios con divisores de un solo dígito y luego probar con divisores de dos, tres, etc. cifras. Con divisores de un dígito, nunca debería tener que revisar al alza o la baja. Por ejemplo, empiece por dividir 123456789 por los dígitos 2, 3, ..., 9. Veamos la división por 9 aquí.
Ejemplo: 123456789÷9 = 13717421
[editar]- Por favor lea el símbolo "->" como: "la tabla de multiplicar sugiere usar ...".
- Como verá, en todos los casos excepto en el último, el dividendo de trabajo es menor que el divisor y necesitamos expandirlo a dos dígitos.
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLMNO | |
| 9 123456789 | 12/9 -> 1 como cociente provisional |
| 9 1123456789 | situar cociente prov. en E |
| -9 | restar 9✕1=9 de FG |
| 9 1 33456789 | 33/9 -> 3 como cociente provisional |
| 9 1333456789 | situar cociente prov. en F |
| -27 | restar 9✕3=27 de GH |
| 9 13 6456789 | 64/9 -> 7 como cociente provisional |
| 9 1376456789 | situar cociente prov. en G |
| -63 | restar 9✕7=63 de HI |
| 9 137 156789 | 15/9 -> 1 como cociente provisional |
| 9 1371156789 | situar cociente prov. en H |
| -9 | restar 9✕1=9 de IJ |
| 9 1371 66789 | 66/9 -> 7 como cociente provisional |
| 9 1371766789 | situar cociente prov. en I |
| -63 | restar 9✕7=63 de JK |
| 9 13717 3789 | 37/9 -> 4 como cociente provisional |
| 9 1371743789 | situar cociente prov. en J |
| -36 | restar 9✕4=36 de KL |
| 9 137174 189 | 18/9 -> 2 como cociente provisional |
| 9 1371742189 | situar cociente prov. en K |
| -18 | restar 9✕2=18 de LM |
| 9 1371742 9 | 9/9 -> 1 como cociente provisional |
| 9 13717421 9 | situar cociente prov. en L |
| -9 | restar 9✕1=9 de MN |
| 9 13717421 | Resto nulo, hecho!
123456789÷9 = 13717421 |
123456789 es un número curioso, es precisamente el producto de 9 por 13717421, ¡un número primo grande!
Ejemplo: 1225 ÷ 35 = 35 Divisor de dos dígitos. Revisando al alza y a la baja
[editar]| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJ | |
| 35 1225 | 12÷3↦4 como cociente provisional |
| +4 | situar cociente prov. en F |
| 35 41225 | Tratar de restar 4✕35 de GHI, |
| -12 | primero 4✕3 de GH |
| 35 40025 | ahora 4✕5 de HI |
| -20 | ¡No se puede! |
| -1 | Revisar a la baja la cifra del cociente |
| 35 30025 | |
| +3 | Devolver lo sustraido en exceso de GH[1] |
| 35 30325 | |
| -15 | continuar normalmente: restar 3✕5 de HI |
| 35 3 175 | 17÷3↦5 como cociente provisional |
| +5 | situar cociente prov. en G |
| 35 35175 | Tratar de restar 5✕35 de HIJ |
| -15 | primero 5✕3 de HI |
| 35 35025 | |
| -25 | ahora 5✕5 de IJ |
| 35 35 | Resto nulo, fin! 1225÷35 = 35 |
Hemos restado 4 × 3 = 12 de 'FGH' , pero si el dígito del cociente correcto es 3, deberíamos haber restado 3 × 3 = 9, por lo que restamos 3 en exceso (solo el primer dígito del divisor ). Debemos devolver este exceso antes de continuar.
Ahora, supongamos que después de nuestra "mala experiencia" revisando a la baja la primera cifra del cociente, y en exceso de prudencia, elegimos 4 como segundo cociente provisional en lugar de 5 como sugiere la tabla de multiplicar. Esta sería la continuación:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHI | |
| 35 3 175 | 17÷3 -> 5, pero usaremos 4 4! |
| +4 | situar cociente prov. en G |
| 35 34175 | Tratamos de sustraer 4✕35 de HIJ |
| -12 | primero 4✕3 = 12 de HI |
| -20 | ahora 4✕5 = 20 de IJ |
| 35 34 20 | ¡Resto mayor o igual al divisor! |
| +1 | Revisar al alza G |
| -20 | restar divisor del resto HI |
| 35 34 | Resto nulo, fin! 1225÷35 = 35 |
Ejemplo 1÷327
[editar]Hasta ahora hemos considerado divisiones entre números naturales con cocientes y residuos, así como números naturales, pero podemos operar con números decimales exactamente como lo hacemos en el cálculo escrito con división larga. Por ejemplo, encontremos el inverso de 327; es decir, 1/327 en un ábaco con 13 columnas.
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 327 1 | 10/3 -> 3 como cociente provisional |
| 327 31 | situar cociente prov. en G |
| -09 | restar 3✕3=9 de HI |
| 327 3 1 | |
| -06 | restar 3✕2=6 de IJ |
| 327 3 4 | |
| -21 | restar 3✕7=21 de JK |
| 327 3 19 | 19/3 -> 6 como cociente provisional |
| 327 30619 | situar cociente prov. en I |
| -18 | restar 6✕3=18 de JK |
| 327 306 1 | |
| -12 | no se puede restar 6✕2=12 de KL! |
| -1 | revisar a la baja I |
| +3 | restaurar el exceso sustraido de JK |
| 327 305 4 | |
| -10 | continuar normalmente, restar 5✕2=10 de KL |
| 327 305 30 | |
| -35 | restar 5✕7=35 de LM |
| 327 305 265 | 36/3 -> 8 como cociente provisional |
| 327 3058265 | situar cociente prov. en J |
| -24 | restar 8✕3=24 de KL |
| 327 3058 25 | |
| -16 | restar 8✕2=16 de LM |
| 327 3058 9 | Resultado hasta aquí: 3058 |
Hemos obtenido como los primeros dígitos de , pero por lo que nuestro resultado es en realidad . Mas abajo daremos una regla para encontrar la varilla unidad de la división.
Ejemplo: 634263 ÷ 79283 = 7,999987 ..., un caso complicado
[editar]Finalmente, obtengamos el primer dígito del cociente de esta división especialmente maliciosa.
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 79283 634263 | 63/7 -> Probamos 9 |
| 79283 9634263 | |
| -63 | restar 9*7=63 de HI |
| 79283 9004263 | |
| -81 | no se puede restar 9*9=81 de IJ! |
| -1 | revisar D a la baja |
| +7 | restaurar lo restado en exceso del dividendo |
| 79283 8 74263 | |
| -72 | continuar restando 8x9=72 de IJ |
| 79283 8 02263 | |
| -16 | restar 8*2=16 de JK |
| 79283 8 00663 | |
| -64 | restar 8*8=64 de KL |
| 79283 8 00023 | no se puede restar 9*3=27 de LM! |
| -1 | revisar D a la baja |
| +7928 | restaurar lo restado en exceso del dividendo |
| 79283 7 79303 | |
| -21 | continuar restando 7x3=21 de LM |
| 79283 7 79282 | cociente: 7, resto: 79283 |
No hay duda de que en este caso redondear el divisor 79283 a 80000 nos habría dado mejores resultados ya que 63÷8 sugiere usar 7 (la cifra correcta) como dígito del cociente provisional.
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 79283 634263 | 63/8 -> probamos 7 |
| 7634263 | |
| -49 | restar 7*7=49 del dividendo HI |
| 79283 7144263 | |
| -63 | restar 7*9=63 del dividendo IJ |
| 79283 7 81263 | |
| -14 | restar 7*2=14 del dividendo JK |
| 79283 7 79863 | |
| -56 | restar 7*8=56 del dividendo KL |
| 79283 7 79303 | |
| -21 | restar 7*3=21 del dividendo LM |
| 79283 7 79282 | cociente: 7, resto: 79283 |
La varilla unidad y los decimales
[editar]La contrapartida de la regla para encontrar la varilla unidad en el caso de la multiplicación es la siguiente regla para la división:
|
La columna de las unidades de los cocientes se ubica columnas a la izquierda de la columna de las unidades del dividendo; donde es el número de dígitos del divisor a la izquierda de su punto decimal (¡que puede ser negativo!). |
La siguiente tabla muestra los valores de para algunos divisores:
| Divisor | n |
|---|---|
| 32.7 | 2 |
| 3.27 | 1 |
| 0.327 | 0 |
| 0.00327 | -2 |
Ejemplo: 1/327 (lo hemos visto arriba)
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJKLM | |
| 327 1 | el divisor tiene 3 dígitos. n=3 |
| . | varilla unidad del dividendo |
| ... | |
| 327 3058 9 | Fin de la división. Resultado: 3058 |
| . | varilla unidad del dividendo |
| <--- | desplazarla n+1 = 4 posiciones a la izquierda |
| . | varilla unidad del cociente |
| 3058 | por lo tanto, ésto... |
| .003058 | ... debe leerse: 0.003058 |
Multiplicación y división como operaciones inversas
[editar]En los cálculos escritos siempre podemos revisar nuestro trabajo para asegurarnos de que no hemos cometido errores y que el resultado obtenido es el correcto. En los cálculos con el ábaco esto no es posible ya que el ábaco no guarda memoria del pasado y de los resultados intermedios. Podemos recurrir a algunos artificios como la prueba del nueve o del once, pero la forma tradicional de verificar los resultados con el ábaco ha sido repetir los cálculos o deshacerlos.
Deshacer sumas y restas es tan simple como partir del resultado y restar lo que hemos sumado y sumar lo que hemos restado; Si hacemos tanto el cálculo como la verificación correctamente, deberíamos terminar con un ábaco limpio, puesto a cero. Para verificar una multiplicación usaremos la división y, recíprocamente, para verificar una división usaremos la multiplicación, sumando el resto si lo hay. Después de hacer esto, devolveremos el ábaco a su estado inicial con los dos operandos originales en sus posiciones de partida. Veamos un ejemplo:
| Ábaco | Comentario |
|---|---|
| ABCDEFGHIJ | |
| 64 2461 | 24/6 -> 4 como cociente provisional |
| 42461 | situar cociente prov. en F |
| -24 | restar 4✕6=24 del dividendo GH |
| 64 4 61 | |
| -16 | no se puede restar 4✕4=16 del dividendo HI |
| -1 | revisar cociente a la baja |
| 64 3 61 | |
| +6 | restaurar lo restado en exceso del dividendo GH |
| 64 3 661 | |
| -12 | continuar normalmente, restar 3✕4=12 del dividendo HI |
| 64 3 541 | 54/6 -> 9, pero vamos a usar 8 |
| 64 38541 | |
| -48 | restar 8✕6=48 del dividendo HI |
| 64 38 61 | |
| -32 | restar 8✕4=32 del dividendo IJ |
| 64 38 29 | cociente: 38, resa 29 |
| La revisión por multiplicación empieza aquí | |
| +48 | sumar 8✕6=48 a HI |
| 64 38509 | |
| +32 | sumar 8✕4=32 a IJ |
| 64 38541 | |
| 64 3 541 | borrar G |
| +18 | sumar 3✕6=18 a GH |
| 64 32341 | |
| +12 | sumar 3✕4=12 a HI |
| 64 32461 | |
| 64 2461 | borrar F. Estado inicial! |
En este libro se ha sugerido usar el número 123456789 para sus primeros ejercicios tanto de multiplicación como de división por un solo dígito. Intente combinarlos con la operación inversa; por ejemplo: divida 123456789 por 9 para obtener 13717421 y multiplique este resultado por 9 para que 123456789 vuelva a la misma posición inicial en el ábaco. O bien comience multiplicando 123456789 por 9 para obtener 1111111101 y luego divida este resultado por 9 para volver al punto de partida. Pruebe todos los dígitos del 2 al 9. Es un buen ejercicio de rutina.
Referencias
[editar]- ↑ Wilson, Jeff. «Long Division Teaching Aid, "Double Division"». Double Division. Archivado desde el original, el March 02, 2021.
- ↑ *Michael R. Williams, Michael R. (1990). «Early Calculation». En Aspray, William. Computing Before Computers. Iowa State University Press,. ISBN 0-8138-0047-1. http://ed-thelen.org/comp-hist/CBC.html.
- ↑ «The Definitive Higher Math Guide on Integer Long Division (and Its Variants)». Math Vault. Archivado desde el original, el May 14, 2021.
Recursos externos
[editar]Hojas de ejercicios
- «The generator». Practicing the soroban.
Otras lecturas
[editar]- «Division». The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle Co., Inc.. 1954. ISBN 978-0-8048-0278-9. https://archive.org/details/japaneseabacus00taka/page/64/mode/2up.
- Heffelfinger, Totton (2004). «Division». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el June 29, 2021.
- Siqueira, Edvaldo (2004). «Decimals & Division». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el May 6, 2021.













































