Curso de alemán nivel medio con audio/Lección 001fm
Apariencia
- índice
- Lección 001fm → Lección 002fm
Fachkurs Mathematik
MMMM
- Zahlenbereiche (Vorbereitungszeit: 1 Stunde - Curso de alemán para principiantes con audio/Lección 089 - Übung Nummer 4129b)
- ---
- Erklären Sie die Zahlenbereiche!
- Warum gibt es verschiedene Zahlenbereiche?
- Wurden diese Zahlenbereiche erfunden oder entdeckt? Begründen Sie ihre Meinung!
- Welche Rechenoperationen sind in welchen Zahlenbereichen möglich?
MMMM

- Zahl
- ---
- Eine Zahl ist ein Zeichen, um eine Menge von Gegenständen oder Menschen zu beschreiben und sich diese Menge besser merken zu können. Mit Zahlen kann man rechnen oder einem anderen Menschen zum Beispiel sagen, wieviel Eis er für sein Geld bekommt.
- ---
- Die einzelnen Zahl-Zeichen von 0 bis 9 nennt man auch Ziffer. Aus mehreren Ziffern kann man auch große Zahlen zusammensetzen, zum Beispiel eine Million aus einer 1 und sechs Nullen.
- ---
- Zahlen gibt es schon seit langer Zeit. Früher waren es einfache Striche, manchmal wurden auch Gegenstände aufgemalt. Die alten Römer nutzten bestimmte Buchstaben als Zahlen, zum Beispiel X für 10 oder M für 1000. Erst sehr viel später übernahm man die arabischen Zahlen, die wir heute verwenden.
- ---
- Die Null ist eine besondere Zahl. Sie ist nicht nur das Zeichen für „Nichts“, sondern hilft auch, große Zahlen zu schreiben. Dabei kommt es nicht nur auf den Wert des Zeichens selbst an, sondern auch darauf, an welcher Stelle es steht. Eine 100 ist deshalb mehr als eine 10, und 1100 ist mehr als 1001.
- ---
- Es gibt auch noch andere besondere Zahlen, die einen eigenen Namen haben, zum Beispiel Pi. Es wird oft mit dem griechischen Buchstaben geschrieben: π. Das sind meistens Zahlen, die in der Wissenschaft eine große Bedeutung haben: Mit Pi etwa kann man ausrechnen, wie groß die Fläche eines Kreises ist.
fuente: Klexikon - CC-BY-SA - fuente/Quelle: http://klexikon.zum.de/wiki/Zahl (Klexikon - die „Wikipedia für Kinder“)
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
MMMM
- Geometrische Formen und geometrische Körper (Vorbereitungszeit: 1 Stunde - Curso de alemán para principiantes con audio/Lección 089 - Übung Nummer 4126; UND: Curso de alemán para principiantes con audio/Lección 123 - Übungen Nummer 5421 und 5422)
- ---
- Erklären Sie die verschiedenen geometrischen Figuren und Formen!
- Wodurch sind sie charakterisiert?
- Wie unterscheiden sie sich voneinander?
MMMM

- Menge
- ---
- Die Menge ist eines der wichtigsten und grundlegenden Konzepte der Mathematik. Man fasst im Rahmen der Mengenlehre einzelne Elemente zu einer Menge zusammen (in der Mathematik insbesondere Zahlen, aber auch z. B. in der Statistik die in einer Stichprobe getesteten Personen, Personen eines Jahrganges, Personen mit Bluthochdruck als vermutetem Risikofaktor für Krankheiten). Eine Menge muss kein Element enthalten (es gibt genau eine Menge ohne Elemente, die „leere Menge“). Bei der Beschreibung einer Menge geht es ausschließlich um die Frage, welche Elemente in ihr enthalten sind. Es wird nicht danach gefragt, ob ein Element mehrmals enthalten ist oder ob es eine Reihenfolge unter den Elementen gibt.
- ---
- In der modernen Mathematik werden die Zahlenbereiche rein mit den Methoden der Mengenlehre (mit der leeren Menge als einzigem Grundbaustein) schrittweise aufgebaut, von den natürlichen Zahlen über die ganzen Zahlen und die rationalen Zahlen zu den reellen Zahlen (und evtl. weiter zu den komplexen Zahlen und noch darüber hinaus).
MMMM
- Mengendiagramm
- ---
- Mengendiagramme dienen der grafischen Veranschaulichung der Mengenlehre. Es gibt unterschiedliche Arten von Mengendiagrammen, insbesondere Euler-Diagramme (nach Leonhard Euler) und Venn-Diagramme (nach John Venn).
- ---
- Euler-Diagramme werden in erster Linie dazu eingesetzt, mengentheoretische Sachverhalte, zum Beispiel die Teilmengeneigenschaft, anschaulich zu machen. Folgende Veranschaulichungen sind üblich:
-
; ist ein Element von .
-
; ist nicht Element von .
-
; ist eine Teilmenge von .
- ---
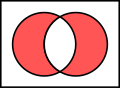
- Venn-Diagramme stellen alle Relationen zwischen den betrachteten Mengen dar. Daher kann man an ihnen Zusammenhänge ablesen und aus dem Vorliegen einzelner Relationen auf das Vorliegen anderer Relationen schließen:
-
(Schnittmenge)
-
(Vereinigungsmenge)
-
(Differenzmenge)
-
(Symmetrische Differenz)
-
(Komplement von A)
MMMM
- Andere Schreibweisen für Mengen
- ---
- Die aufzählende Schreibweise M = { blau, gelb, rot } kann als eine Abkürzung für die umständlichere Schreibweise M = { x | x = blau oder x = gelb oder x = rot } verstanden werden.
- Bei der Schreibweise mit Auslassungspunkten werden nur einige Elemente als Beispiele aufgeführt, etwa: M = { 3, 6, 9, 12, …, 96, 99 }. Sie ist nur verwendbar, wenn das Bildungsgesetz aus diesen Beispielen oder aus dem Zusammenhang klar ist. Hier ist offenbar die Menge gemeint, die sich intensional als M = { x | x ist eine durch 3 teilbare Zahl zwischen 1 und 100 } schreiben lässt. Diese Schreibweise wird häufig für unendliche Mengen angewendet. So beschreibt G = { 4, 6, 8, 10, … } die Menge der geraden natürlichen Zahlen, die größer sind als 2.
MMMM
- Funktion
- ---
- In der Mathematik ist eine Funktion oder Abbildung eine Beziehung (Relation) zwischen zwei Mengen, die jedem Element der einen Menge (x-Wert) genau ein Element der anderen Menge (y-Wert) zuordnet.
- Das Konzept der Funktion oder Abbildung nimmt in der modernen Mathematik eine zentrale Stellung ein.
- Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y einer Zielmenge Z zu.
- Die Umkehrung gilt nicht: Ein Element der Zielmenge kann einem, mehreren, aber auch keinem Element der Definitionsmenge zugeordnet sein.
- ---
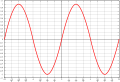
- Beispiele einiger Funktionsgraphen:
-
Lineare Funktion
-
Polynomfunktion 5. Grades
-
Sinusfunktion
-
Gaußsche Glockenkurve
MMMM
- Punkt, Strecke, Gerade, Linie
- ---
- Ein Punkt (als Raumpunkt) ist ein grundlegendes Element der Geometrie. Anschaulich stellt man sich darunter ein Objekt ohne jede Ausdehnung vor.
- Der Punkt ist ein spezieller Kreis mit einem Radius von null.
- Der Punkt ist etwas, das keine Teile hat.
- „Ein Punkt ist genau das, was der intelligente, aber harmlose, unverbildete Leser sich darunter vorstellt.“
- Obwohl Punkte keine Ausdehnung haben, haben die aus ihnen zusammengesetzt vorgestellten Linien eine Ausdehnung.
- ---

- Eine Strecke (auch Geradenabschnitt oder Geradenstück) ist eine gerade Linie, die von zwei Punkten begrenzt wird; sie ist die kürzeste Verbindung ihrer beiden Endpunkte. Die Begrenzung einer Strecke durch diese Punkte unterscheidet sie von Geraden, die beidseitig unbegrenzt sind, und von Halbgeraden, die nur auf einer Seite begrenzt sind.
- abgeschlossene Strecke [AB]: beide Endpunkte sind eingeschlossen
- offene Strecke (AB): beide Endpunkte sind ausgeschlossen
- halboffene Strecke [AB) bzw. (AB]: einer der Endpunkte ist eingeschlossen, der andere ausgeschlossen
- ---

- Eine gerade Linie oder kurz Gerade ist ein Element der Geometrie. Die kürzeste Verbindung zweier Punkte ist gerade und wird als Strecke bezeichnet. Eine gerade, unendlich lange, unendlich dünne und in beide Richtungen unbegrenzte Linie nennt man eine Gerade.
- Eine Gerade ist eine Menge von Punkten.
MMMM

- Mathematik
- ---
- unendlich
- ---
- Der Begriff Unendlichkeit bezeichnet die Negation bzw. Aufhebung von Endlichkeit, weniger präzise auch deren „Gegenteil“. Sein mathematisches Symbol ist das Unendlichzeichen (∞). Theoretisch beschreibt der Begriff „unendlich“ ein Objekt, welches kein Ende oder Schluss hat, aber einen Anfang oder Beginn haben kann, in der Geometrie würde also ein Strahl oder eine Kreisbahn als unendlich beschrieben werden.
- ---
- Die Unendlichkeit lässt sich geistes- oder naturwissenschaftlich nur abstrakt in der Vorstellung entwickeln und wird auf Objekte und Begriffe angewendet, die keine räumlichen oder zeitlichen Grenzen haben.
- ---
- In der Mathematik gibt es keinen definierten Begriff mit dem Namen „Unendlichkeit“, jedoch wird das Adjektiv unendlich zur näheren Charakterisierung einiger mathematischer Begriffe verwendet. In der Regel ist diese Charakterisierung komplementär zum Begriff endlich. Ein Beispiel für solch eine Begriffsbildungen ist:
- unendliche Menge als komplementärer Begriff zur endlichen Menge.
- ---
- Unendliche Werte werden in der Mathematik durch das Unendlichzeichen ∞ dargestellt. Dieses Symbol wurde 1655 von dem englischen Mathematiker John Wallis als Zeichen für eine abstrakte unendliche Größe eingeführt.
MMMM

- Pi
- ---
- Die Kreiszahl π (Pi) ist eine mathematische Konstante, die als Verhältnis des Umfangs eines Kreises zu seinem Durchmesser definiert ist. Dieses Verhältnis ist unabhängig von der Größe des Kreises.
- Pi ist eine irrationale Zahl und kommt in zahlreichen Teilgebieten der Mathematik, auch außerhalb der Geometrie, vor.
- Die Kreiszahl Pi beginnt mit:
- π = 3,1415926...
- Die Kreiszahl und manche ihrer Eigenschaften waren bereits in der Antike bekannt, die Bezeichnung mit dem griechischen Buchstaben Pi (π) (nach dem Anfangsbuchstaben des griechischen Wortes „peripheria“ („Randbereich“) bzw. perimetros („Umfang“) wurde im 18. Jahrhundert durch Leonhard Euler populär.
- ---
- Die Zahl π ist eine irrationale Zahl, also eine reelle, aber keine rationale Zahl. Das bedeutet, dass sie nicht als Verhältnis zweier ganzer Zahlen p, q, also nicht als Bruch p/q dargestellt werden kann.
- Da π eine irrationale Zahl ist, ist die Darstellung stets unendlich lang und nicht periodisch. Bei den ersten 100 Nachkommastellen ist keine Regelmäßigkeit ersichtlich.
- π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 …
- Auch weitere Nachkommastellen genügen statistischen Tests auf Zufälligkeit.
- ---
- Erste Schätzungen
- ---
- Aus praktischen Erwägungen heraus versuchten die Menschen schon in sehr früher Zeit, dem Phänomen Kreis näherzukommen. So ist das Verhältnis vom Umfang zum Durchmesser eines Kreises beispielsweise wichtig für die Berechnung der Länge des Beschlages eines Rades, der Fläche eines runden Feldes oder des Rauminhalts eines zylindrischen Getreidespeichers.
- Als Näherung für π benutzten die Babylonier einfach nur 3 oder auch 3,125.
- Handwerker benutzten in Zeiten vor Rechenschieber und Taschenrechner die Näherung 22/7 ≈ 3,142857 und berechneten damit vieles im Kopf. Der Fehler gegenüber \pi beträgt etwa 0,04 %. Für alltägliche praktische Situationen war das völlig ausreichend.
MMMM
- Primzahl
- ---
- Eine Primzahl ist eine natürliche Zahl, die größer als 1 und ausschließlich durch sich selbst und durch 1 ganzzahlig teilbar ist. Eine Primzahl ist also eine natürliche Zahl, die genau zwei natürliche Zahlen als Teiler hat. Die kleinsten Primzahlen sind:
- P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...}
- ---
- Eine natürliche Zahl größer als 1 heißt prim, wenn sie eine Primzahl ist, andernfalls heißt sie zusammengesetzt. Die Zahlen 0 und 1 sind weder prim noch zusammengesetzt.
- Das Wort „Primzahl“ kommt aus dem Lateinischen (numerus primus) und bedeutet „die erste Zahl“.
- Die Primzahlen P haben für viele Bereiche der Mathematik eine Bedeutung.
- Primzahlen lassen sich nicht als Produkt zweier natürlicher Zahlen, die beide größer als 1 sind, darstellen.
- Jede natürliche Zahl, die größer als 1 und selbst keine Primzahl ist, lässt sich als Produkt von mindestens zwei Primzahlen schreiben. Diese Produktdarstellung ist bis auf die Reihenfolge der Faktoren eindeutig.
- Schon im antiken Griechenland interessierte man sich für die Primzahlen und entdeckte einige ihrer Eigenschaften. Obwohl Primzahlen seit damals stets einen großen Reiz auf die Menschen ausübten, sind viele die Primzahlen betreffenden Fragen bis heute ungeklärt, darunter solche, die mehr als hundert Jahre alt und leicht verständlich formulierbar sind.
- Noch nicht bewiesen ist die „Goldbachsche Vermutung“, wonach außer 2 jede gerade Zahl als Summe zweier Primzahlen darstellbar ist.
- Auch noch nicht beweisen ist die Vermutung, dass es unendlich viele Primzahlzwillinge gibt (das sind Paare von Primzahlen, deren Differenz gleich 2 ist).
- Über 2000 Jahre lang konnte man keinen praktischen Nutzen aus dem Wissen über die Primzahlen ziehen. Dies änderte sich erst mit dem Aufkommen elektronischer Rechenmaschinen, bei denen die Primzahlen beispielsweise in der Kryptographie eine zentrale Rolle spielen.
MMMM
- Eigenschafen von Primzahlen
- ---
- Mit Ausnahme der Zahl 2 sind alle Primzahlen p ungerade, denn alle größeren geraden Zahlen lassen sich außer durch sich selbst und 1 auch noch (mindestens) durch 2 teilen. Damit hat jede Primzahl außer 2 die Form 2k+1 mit einer natürlichen Zahl k.
- ---
- Größte bekannte Primzahl
- ---
- Der Grieche Euklid hat im vierten Jahrhundert vor Christus logisch geschlussfolgert, dass es unendlich viele Primzahlen gibt; diese Aussage wird als Satz von Euklid bezeichnet. Euklid führte einen Widerspruchsbeweis für die Richtigkeit dieses Satzes.
- Der Satz von Euklid besagt, dass es keine größte Primzahl gibt. Es ist jedoch kein Verfahren bekannt, das effizient beliebig große Primzahlen generiert – deshalb gab es stets eine jeweils größte bekannte Primzahl, seitdem sich die Menschen mit Primzahlen befassen. Derzeit ist es 2 hoch 274.207.281 − 1, eine Zahl mit 22.338.618 (dezimalen) Stellen, die am 7. Januar 2016 berechnet wurde.
- Die Differenz zwischen zwei benachbarten Primzahlen heißt Primzahllücke. Diese Differenz schwankt, und es gibt Primzahllücken beliebiger Größe.
MMMM
- Generierung von Primzahlen
- ---
- Einer der ältesten Algorithmen zur Bestimmung von Primzahlen ist das Sieb des Eratosthenes. Bis heute ist kein effizienter Primzahlgenerator bekannt.
- Das Sieb des Eratosthenes ist ein Algorithmus zur Bestimmung einer Liste oder Tabelle aller Primzahlen kleiner oder gleich einer vorgegebenen Zahl. Er ist nach dem griechischen Mathematiker Eratosthenes von Kyrene benannt. Allerdings hat Eratosthenes, der im 3. Jahrhundert v. Chr. lebte, das Verfahren nicht entdeckt, sondern nur die Bezeichnung „Sieb“ für das schon lange vor seiner Zeit bekannte Verfahren eingeführt.
- ---

- Das Sieb des Eratosthenes ist ein Algorithmus zur Bestimmung einer Liste oder Tabelle aller Primzahlen kleiner oder gleich einer vorgegebenen Zahl. Er ist nach dem griechischen Mathematiker Eratosthenes von Kyrene benannt. Allerdings hat Eratosthenes, der im 3. Jahrhundert v. Chr. lebte, das Verfahren nicht entdeckt, sondern nur die Bezeichnung „Sieb“ für das schon lange vor seiner Zeit bekannte Verfahren eingeführt.
- ---
- Zunächst werden alle Zahlen 2, 3, 4,… bis zu einem frei wählbaren Maximalwert S aufgeschrieben. Die zunächst unmarkierten Zahlen sind potentielle Primzahlen. Die kleinste unmarkierte Zahl ist immer eine Primzahl. Nachdem eine Primzahl gefunden wurde, werden alle Vielfachen dieser Primzahl als zusammengesetzt markiert. Man bestimmt die nächstgrößere nicht markierte Zahl. Da sie kein Vielfaches von Zahlen kleiner als sie selbst ist (sonst wäre sie markiert worden), kann sie nur durch eins und sich selbst teilbar sein. Folglich muss es sich um eine Primzahl handeln. Diese wird dementsprechend als Primzahl ausgegeben. Man streicht wieder alle Vielfachen und führt das Verfahren fort, bis man am Ende der Liste angekommen ist. Im Verlauf des Verfahren werden alle Primzahlen ausgegeben.
- ---
- Das obenstehende Bild demonstriert das Verfahren, wie die Primzahlen zwischen 2 und 120 ermittelt werden: Erst werden alle Vielfachen von 2 gestrichen, dann alle Vielfachen von 3, 5, und 7. Die Markierungen beginnen jeweils mit dem Quadrat der Primzahl: 4, 9, 25, 49. Da bereits 112 = 121 nicht mehr im Wertebereich liegt, werden ab 11 keine zusammengesetzten Zahlen mehr markiert; alle noch unmarkierten Zahlen sind prim.
MMMM
- Endliche und unendliche Mengen
- ---
- Aus Zahlen kann man Mengen bilden:
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M5 = {0; 22; 27}
- M6 = {7; 8; 9; 10}
- Die Menge M1 besteht aus drei Elementen. „4, 5, 6“ sind die Elemente der Menge M1. „4“ ist ein Elemtne der Menge M1.
- Man schreibt: „4 ∈ M1“.
- Man liest: „4 ist ein Element der Menge M1“ oder „4 ist ein Element aus M1“.
- Die Menge M1 hat drei Elemente. Das sind endlich viele Elemente. Deshalb heißt die Menge M1 eine „endliche Menge“.
- Auch die Menge M2 ist eine endliche Menge, weil sie aus endlich vielen Elemente besteht.
- Die Mengen M1, M2, M3, M4, M5 und M6 sind endliche Mengen.
- Betrachte Sie die Mengen M2 und M6! Sie sind gleich, weil sie aus den gleichen Elemente bestehen.
- MERKE: Zwei Mengen sind gleich, wenn sie aus den gleichen Elementen bestehen.
- Alle Elemente der Mengen M1 bis M6 sind natürliche Zahlen.
- Die Menge ℕ = {0; 1; 2; 3; 4; 5; 6; 7; ... } heißt Menge der natürlichen Zahlen. Die Menge ℕ ist keine endliche, sondern eine unendliche Menge, weil sie aus unendlich vielen Elementen besteht.
- ---
- Mengenschreibweise:
- Die Menge wird gewöhnlich mit einem großen Buchstaben bezeichnet, hier ein „M“. Um verschiedene Menge zu benennen können entweder unterschiedliche Großbuchstaben verwendet weden oder bei gleichen Buchstaben ein Indix (eine tiefergestellte zahl, mit der die Mengen nacheinander nummeriert werden).
- Die Elemente der Menge werden in geschweiften Klammern - {geschweifte Klammer} - geschrieben, wobei die einzelnen Elemente durch ein Komma oder Semikolon getrennt werden. Hier wurde wegen der Zahlen ein Semikolon verwendet, damit es keine Verwechslungen mit dem Dezimalkomma geben kann.
- Die Reichenfolge der Elemente innterhalb der geschweiften Klammern ist egal.
- M7 = {2; 4; 6}
- M8 = {4; 6; 2}
- Deshalb sind die Mengen M7 und M8 identisch (gleich).
MMMM

- Mengen und Teilmengen
- ---
- Die Menge M1 ist eine Teilmenge der Menge ℕ.
- Man schreibt: M1 ⊆ ℕ
- Man liest: „M1 ist Teilmenge von N“.
- Die endliceh Menge M1 ist eine Teilmenge der unendlichen Menge ℕ.

- Für die Mengen M1, M2, M3 und M4 gilt:
- M1 ⊆ M3 und M4 ⊆ M2
- ---
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M5 = {0; 22; 27}
- M6 = {7; 8; 9; 10}
- ---
- Unter welchen Bedingungen ist eine Menge A Teilmenge der Menge B?
Lösung M79 - MERKE: - MERKE: Eine Menge A ist eine Teilmenge der Menge B, wenn alle Elemente aus A auch Element von B sind.

Teilmenge - Beispiel:
- A = {1; 9; 11}
- B = {1; 4; 8; 9; 11}
- A ⊆ B
- Man kann diesen Satz auch folgendermaßen formulieren: Wenn für alle Elemente x aus A gilt, dass x Element aus B ist, so ist A eine Teilmenge von B.
- Diesen Satz kann man mit Hilfe von Symbolen schreiben:
- Für Konditionalsätze der Form: „Wenn H1, so H2“ benutzt man das Symbol „Wenn H1 → H2“.
- Für den sprachlichen Ausdruck: „Für alle Elemente x aus A gilt, dass ...“
- benutzt man das Symbol „∀x ∈ A: ... “.
- ---
- Der obige Satz erhält nun folgende Form: (∀x ∈ A: x ∈ B) → A ⊆ B.
MMMM
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M5 = {0; 22; 27}
- M6 = {7; 8; 9; 10}
- ---
- Betrachten Sie die Mengen M3 und M4! Ist M4 eine Teilmenge von M3? Nein, M4 ist keine Teilmenge von M3, denn nicht für alle Elemente x aus M4 gilt, dass x aus M ist. Man schreibt: M4 ⊈ M3 und ~∀x ∈ M4: x ∈ M3.
- Zum Beispiel ist 9 ∈ M4, aber 9 ist keine Element aus M3. Man schreibt 9 ∉ M3.
MMMM
- Unendliche Teilmengen
- ---
- Gibt es auch unendliche Teilmengen der Menge ℕ?
- Ja, z. B. sind Ng = {0; 2; 4; 6; ... ; 2n; ... } und Nu = {1; 3; 5; 7; ...; 2n+1; ... } unendliche Teilmengen der menge ℕ. (Das „g“ in Ng steht für „gerade Zahlen“ und das „u“ in Nu für „ungerade Zahlen“.)
- Die Zahl 2n steht für alle n ∈ ℕ, die eine gerade Zahl sind. (∀n ∈ ℕ: 2n ∈ Ng). Entsprechend ist 2n + 1 eine ungerade Zahl.
- Die Menge Ng der geraden Zahlen und die Menge Nu der ungeraden Zahlen sind unendliche Teilmengen der Menge ℕ.
- ---
- Betrachten Sie die Mengen M2 und M6! Ist M2 eine Teilmenge der Menge M6?
- Ja, denn für alle Elemente x aus M2 gilt, dass x aus M6 ist.
- ∀n ∈ M2: x ∈ M6; also M6 ⊆ M2.
- Allgemein gilt:
- MERKE: Für jede Menge A gilt, dass A Teilmenge von A ist. ∀A: A ⊆ A
MMMM
- Betrachten Sie nun die Mengen M4 und M2!
- ---
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M5 = {0; 22; 27}
- M6 = {7; 8; 9; 10}
- ---
- Die Menge M4 heißt echte Teilmenge der Menge M2.
- Man schreibt: M4 ⊂ M2.
- Man liest: „M4 ist eine echte Teilmenge von M2“.
- ---
- M4 ⊂ M2, weil M4 ⊆ M2 ist und weil es das Element 7 aus M2 gibt, so dass 7 ∉ M4 ist.
- Allgemein gilt:
- MERKE: Wenn A eine Teilmenge von B ist und wenn wenn es mindestens ein Element x aus B gibt, so dass x kein Element aus A ist, ist A eine echte Teilmenge von B.


MMMM
- Für den sprachlichen Ausdruck: „Es gibt mindestens ein Element x aus A, so dass ... “ benutzt man das Symbol „∃x ∈: ... “.
- Außerdem benutzt man für „und“ das Symbol „∧“. Deshalb kann man kürzer schreiben:
- (A ⊆ B ∧ ∃x ∈ B: x ∉ A) → A ⊂ B
- ---
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M5 = {0; 22; 27}
- M6 = {7; 8; 9; 10}
- ---
- Weiter Beispiele für echte Teilmengen sind:
- M1 ⊂ M3 und M4 ⊂ M6
MMMM
- Natürliche Zahlen
- ---
- Eigenschaften der Menge ℕ
- ---
- Die natürlichen Zahlen und die Operationen mit ihnen wie z. B. das Addieren, das Subtrahieren und das Multiplizieren haben ihren Ursprung in der alltäglichen Praxis.
- In der realen Welt existieren Mengen von realen Objekten, und die Menschen haben in langer geschichtlicher Entwicklung das rein quantitative Charakterisieren dieser Mengen durch natürliche Zahlen gelernt.
- ---
- So werden unabhängig von ihrer qualitativen Zusammensetzung alle Mengen mit der gleichen Anzahl von Objekten durch die gleich natürliche Zahl quantitativ charakterisiert. Die Praxis hat von den Menschen verlangt, dass sie Mengen von realen Objekten quantitativ vergleichen und mehrere Mengen zu einer einzigen vereinigen können. Es war also die jahrhundertelange Praxis der Menschen im Bilden und Vergleichen von Mengen realer Objekte, die zu den abstrakten Begriffen wie z. B. „natürliche Zahl“, „kleiner“, „größer“, „gleich“, „addieren“, „subtrahieren“ und „multiplizieren“ führte.
MMMM
- Durch Vergleichen der natürlichen Zahlen und durch Ausführen von Rechenoperationen mit natürlichen Zahlen erkennt man die Eigenschaften der Menge der natürlichen Zahlen.
- Die Menge N der natürlichen Zahlen hat unendlich viele Elemente. Das erste Element ist die Zahl „null“, das nächste die Zahl „eins“. Dann folgt die Zahl „zwei“ usw.
- Die Menge N ist eine unendliche Menge.
- ---
- Die Menge N hat noch andere wichtige Eigenschalten:
- 1.)
- Wenn n und m zwei beliebige natürliche Zahlen sind, so ist entweder n < m (n kleiner als m) oder n > m oder n = m.
- ∀n, m , k ∈ ℕ: entweder n < m oder n = m oder n > m
- 2.)
- Wenn für drei natürliche Zahlen n, m und k die Relationen r < m und m < k gelten, so ist auch n < k.
- ∀n, m , k ∈ ℕ: [(n < m ∧ m < k) → n < k]
- ---
- Wenn eine Menge diese Eigenschaft besitzt, so nennt man sie eine geordnete Menge.
- Die Menge ℕ der natürlichen zahlen ist eine unendliche, geordnete Menge.
- ---
- Aus der Relation n < m fo1gt, dass m > n (m größer als n) ist.
- n ≦ m (gelesen: n kleiner oder gleich m) heißt, dass n < m oder n = m ist.
- Die Negation von n < m ist die Relation n ≧ m. Entsprechend ist die Negation von n ≦ m die Relation n > m. n ≠ m liest man: „n ungleich m“.
MMMM



- Geometrische Darstellung der natürlichen Zahlen
- ---
- Man kann die natürlichen Zahlen auf einer Geraden darstellen. Man ordnet der Zahl 0 einen beliebigen Punkt P0 der Geraden zu. Man ordnet der Zahl 1 einen Punkt P1 zu.
- In den gleichen Abständen l () werden weitere Punkte gewählt.Dadurch kann man jeder natürlichen Zahl genau einen Punkt dieser Zahlengeraden zuordnen. Man kann aber nicht jedem Punkt auf der Zahlengeraden eine natürliche Zahl zuordnen.
- ---
- Zahlengerade
- Unter Zahlengerade versteht man im Mathematikunterricht die Veranschaulichung der natürlichen und reellen Zahlen als Punkte auf einer Geraden.
- Die Zahlengerade dient zur Veranschaulichung der natürlichen und reellen Zahlen.
- Die Zahlengerade setzt sich in beide Richtungen bis ins Unendliche fort. Der Pfeil an der rechten Seite der Darstellung gibt an, dass die Zahlen in dieser Richtung größer werden.
MMMM
- Grundrechenarten in der Menge ℕ
- ---
- Addition
- ---
- Durch die Addition ordnet man zwei gegebenen natürlichen Zahlen n und m eine dritte Zahl s zu. Man schreibt n + m = s. Die Glieder n und m heißen Summanden, n + m (n plus m) ist die Summe aus n und m, sie hat den Wert s.
- ---
- Die Addition in N hat folgende Eigenschaften:
- 1.) Wenn man eine beliebige natürliche Zahl m zu einer beliebigen natürlichen Zahl n addiert, so erhält man wieder eine natürliche Zahl s. Die Addition ist in der Menge N stets ausführbar.
- ∀n, m ∈ ℕ: ∃s ∈ ℕ: n + m = s
- 2.) Wenn man m zu n addiert, so gibt es genau ein Resultat s.
- ∀m, n ∈ ℕ: ∃!!s ∈ ℕ: n + m = s
- Die Addition in der Menge N ist eine eindeutige Operation.
- 3.) Bei Summen aus mehr als zwei Summanden spielt es keine Rolle, welche Summanden man zuerst addiert. Für die Addition gilt das Assoziativgesetz:
- n + m + k = (n + m) + k = n + (m + k)
- 4.) Der Wert einer Summe ändert sich nicht, wenn man die Summanden miteinander vertauscht.
- Für die Addition gilt das Kommutativgesetz:
- n + m = m + n
MMMM

- Subtraktion
- ---
- Subtraktion ist eine Rechenart in der Mathematik. Dabei zieht man von einer Zahl eine andere ab. Das Rechenzeichen dafür ist das Minus, das durch den Minusstrich - aufgeschrieben wird. Dieses Zeichen hat sich im Jahr 1489 der Mathematiker Johannes Widmann ausgedacht.
- ---
- Nimmt man von 10 Dingen zwei weg, bleiben acht übrig. Das kann man so aufschreiben: 10-2=8, gesprochen: Zehn minus Zwei ergibt Acht. Die Zahl, von der etwas abgezogen wird, heißt „Minuend“ (lateinisch „der zu verringernde“). Die Zahl, die abgezogen wird, heißt „Subtrahend“ (lateinisch „der abzuziehende“). Das Ergebnis einer Subtraktion ist die „Differenz“.
- ---
- Ein praktisches Beispiel, bei dem man subtrahieren, also eine Subtraktion durchführen muss: Man möchte ein Brötchen kaufen. Dieses Brötchen kostet 1 Euro. Man hat 3 Euro im Portemonnaie. Man rechnet also folgendes: 3-1=2. Nachdem man das Brötchen gekauft hat, hat man noch 2 Euro übrig.
fuente: Klexikon - CC-BY-SA - fuente/Quelle: http://klexikon.zum.de/wiki/Subtraktion (Klexikon - die „Wikipedia für Kinder“)
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
MMMM

- Addition
- ---
- Addition ist eine Rechenart in der Mathematik. Dabei zählt man eine Zahl zu einer anderen hinzu. Das Rechenzeichen dafür ist das Plus, das durch das Pluszeichen + aufgeschrieben wird. Dieses Zeichen hat sich im Jahr 1489 der Mathematiker Johannes Widmann ausgedacht.
- ---
- Fügt man zu zehn Dingen zwei hinzu, hat man zwölf Dinge. Das kann man so aufschreiben: 10+2=12, gesprochen: Zehn plus Zwei ergibt Zwölf. Die Zwölf ist das Ergebnis der Addition. Man sagt dazu auch „Summe“. Die beiden Zahlen, die addiert werden, nennt man „Summanden“.
- ---
- Angenommen, man hat zwei Äpfel und möchte drei weitere Äpfel kaufen. Wenn man sie gekauft hat, hat man insgesamt fünf Äpfel. Man rechnet also: 2+3=5.
fuente: Klexikon - CC-BY-SA - fuente/Quelle: http://klexikon.zum.de/wiki/Addition (Klexikon - die „Wikipedia für Kinder“)
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
MMMM
- Multiplikation (Teil 1)
- ---

- Bei der Multiplikation nimmt man zwei Zahlen miteinander „mal“. Als Rechenzeichen schreibt man einen Punkt: · Weil man den aber auf dem Bildschirm oder der Tastatur nicht so gut sieht, nimmt man dort lieber ein Kreuz: ×
- Multiplikation ist eine Art, Zahlen, die man immer mit sich selbst addieren würde, kürzer aufzuschreiben. Dazu ein Beispiel: man möchte rechnen. Dies kann man vereinfacht auch als 4 × 3 schreiben (gesprochen: vier mal drei), da man vier mal die Zahl drei mit sich selbst addiert. Zahlen, die man miteinander multipliziert, werden Faktoren genannt, das Ergebnis heißt Produkt.
fuente: Klexikon - CC-BY-SA - fuente/Quelle: http://klexikon.zum.de/wiki/Grundrechenarten (Klexikon - die „Wikipedia für Kinder“)
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
MMMM
- Multiplikation (Teil 2)
- ---
- Die Multiplikation (lateinisch multiplicatio, von multiplicare ‚vervielfachen‘, auch Malnehmen genannt) ist eine der vier Grundrechenarten in der Arithmetik. Ihre Umkehroperation ist die Division (das Teilen). Das Rechenzeichen für die Multiplikation ist das Malzeichen „·“ bzw. „ד.
- ---
- Namensgebung der Multiplikation:
- Die Multiplikation natürlicher Zahlen entsteht durch das wiederholte Addieren (Zusammenzählen) des gleichen Summanden:
- a und b nennt man Faktoren, wobei a auch als Multiplikator und b auch als Multiplikand bezeichnet werden.
- Die Rechnung, gesprochen „a mal b“, heißt Multiplikation. Das Ergebnis Produkt.
- Merkhilfe:
- Produkt = 1. Faktor · 2. Faktor bzw. 2. Faktor · 1. Faktor = Produkt
- oder
- Produkt = Multiplikand · Multiplikator bzw. Multiplikator · Multiplikand = Produkt.
- Zum Beispiel schreibt man 3 · 4 für 4 + 4 + 4, und spricht diesen Term als „drei mal vier“. Anstelle von 3 · 4 wird manchmal auch 3 × 4 oder 3 * 4 geschrieben.
- Bei der Multiplikation mit Variablen wird der Punkt oft weggelassen (5x, xy). Zur richtigen Schreibweise siehe weiter unten: Malzeichen.
- ---
- Rechenregeln der Multiplikation:
Assoziativgesetz Kommutativgesetz Distributivgesetz
- ---
- Das Produkt von mehr als zwei Faktoren wird so definiert, dass man von links beginnend je zwei Faktoren multipliziert und so fortfährt, bis nur eine Zahl übrigbleibt. Das Assoziativgesetz besagt nun, dass man an beliebiger Stelle beginnen kann; also auch von rechts. Aufgrund des Kommutativgesetzes ist auch die Reihenfolge irrelevant, so dass mit zwei beliebigen Faktoren (welche also nicht direkt beieinanderstehen müssen) angefangen werden kann.
MMMM
- Malzeichen
- ---
- Als Malzeichen oder Produktsymbole werden verschiedene Sonderzeichen bezeichnet, die unter anderem zur Darstellung des mathematischen Operators für die Multiplikation verwendet werden. Für die Multiplikation wird normalerweise der Malpunkt · verwendet, seltener auch das Malkreuz × und speziell in Programmiersprachen als Ersatzzeichen das Sternchen *.
- ---
- Geschichte:
- Das älteste Symbol scheint das Malkreuz (×) zu sein. Verwendet wurde es erstmals von dem englischen Mathematiker William Oughtred in seinem Werk Clavis Mathematicae, veröffentlicht 1631 in London. Wahrscheinlich benutzte Oughtred das Malkreuz schon seit 1618, falls ein anonymer Anhang zur englischen Übersetzung von John Napiers Descriptio von ihm stammt. Die Herleitung des Symbols – vom Buchstaben (X) oder auch vom Andreaskreuz – ist nicht geklärt.
- Der deutsche Wissenschaftler Gottfried Wilhelm Leibniz lehnte das Malkreuz wegen der Verwechslungsgefahr mit dem Buchstaben X ab und bevorzugte den Punkt (·). Leibniz benutzte den Multiplikationspunkt in einem Briefwechsel des Jahres 1698, hat ihn aber wahrscheinlich schon 1694 oder noch früher in seine mathematische Notation eingeführt.
- Johann Rahn führte den Stern (∗) für die Multiplikation ein. Zusammen mit dem Symbol für die Division (÷) erscheint dieser erstmals in seinem Buch Teutsche Algebra, veröffentlicht 1659.
- ---
- In der Grundrechenart Multiplikation sind der Malpunkt · und das Malkreuz × inhaltlich gleichbedeutend, sie werden aber unterschiedlich verwendet.
- Das Malkreuz × wird eingesetzt
- wenn die Multiplikation optisch auffallend dargestellt werden muss, etwa auf einem Plakat:
- 5 × 2 Freikarten!
- wenn die Faktoren nicht Formelzeichen oder Zahlen sind, sondern Wörter:
- Gewerbesteuer = Steuermessbetrag × Hebesatz
- wenn nur der linke Faktor angegeben ist, also im Sinne von -mal oder -fach:
- Vergrößerung: 6×
- in angloamerikanisch geprägten Kulturen sowie in Frankreich im Schulunterricht und Alltag.
- Der Malpunkt · wird dagegen benutzt,
- wenn Berechnungen mit Formelzeichen und Zahlen wiedergegeben werden:
- a = 5 · x² + 7
- in Deutschland im Schulunterricht.
- ---
- Bei wissenschaftlichen Berechnungen wird der Malpunkt dann ganz weggelassen, wenn die Gestaltung es erlaubt und aus dem Kontext heraus keine Verwechslungsgefahr besteht.
- U = 2πr – ohne Leerraum
U = 2 π r – schmales Leerzeichen
U = 2 π r – Leerzeichen
Gleichheitszeichen (und entsprechende) werden durch vergrößerten Leerraum hervorgehoben - In einigen Programmiersprachen wird das Sternchen
*benutzt. - ---
- Abmessungen:
- Bei der Angabe von Abmessungen wie zum Beispiel Breite × Länge wird ebenfalls das Malkreuz verwendet. Beispielhafte Verwendungen sind:
- eine Fläche von 3 m × 5 m
- das Grundstück ist 30 × 40 m groß
- Die Angabe von Abmessungen stellt keine Multiplikation der jeweiligen Längen dar. Die Maßeinheit kann dabei, wie im zweiten Beispiel, auch nur einmal angegeben werden.
MMMM
- Schriftliche Addition
| 3 | 1 | 6 | 5 | |
| + | 1 | 5 | 2 | 3 |
| 4 | 6 | 8 | 8 | |
- ---
3 4 2 7 8 9 5 1 4 3 3 5 1 4
- Erklärung: 9 + 5 = 14. Schreibe die 1 als Übertrag in die Hilfszeile und die 4 als Ergebnis in die Ergebniszeile:
- ---
- Zwischenergebnis:
3 4 2 7 8 9 5 1 4 3 3 5 1 1 1 7 1 2 4
- ---
- Endergebnis:
3 4 2 7 8 9 5 1 4 3 3 5 1 1 1 8 5 7 1 2 4
MMMM
- Schriftliche Addition
- ---
- Bei dem Verfahren, das u. a. im deutschsprachigen Raum an den Grundschulen gelehrt wird, werden die zu addierenden Zahlen in der Darstellung des Dezimalsystems so übereinander geschrieben, dass entsprechende Stellen untereinander stehen (Einer über Einern, Zehner über Zehnern usw.). Die Ziffern werden dann – von rechts nach links – Stelle für Stelle addiert; das Zwischenergebnis wird unten notiert, jedoch nur die letzte Stelle. Ist das Zwischenergebnis mehrstellig, so entstehen Überträge, die beim Abarbeiten der jeweils nächsten Spalte berücksichtigt werden müssen. Für die Durchführung des Verfahrens ist es erforderlich die Summen von Zahlen zwischen 0 und 9 auswendig zu wissen.
Beispiel:
-
2+1=3
-
5+7=12
Die 1 wird als Übertrag der nächsten (links benachbarten) Ziffernspalte zugeschlagen. -
1+6+4=11
MMMM
- Schriftliche Subtraktion
- ---
- In den Grundschulen werden heute meist Verfahren gelehrt, bei denen die einander entsprechenden Stellen der Minuenden und Subtrahenden übereinander stehen. Die Stellen werden nacheinander abgearbeitet, meist von rechts nach links.
- Für das schriftliche Subtrahieren muss der Minuend (Zahl oben) größer oder gleich dem Subtrahenden (Zahl(en) unten) sein. Negative Ergebnisse sind somit direkt nicht möglich.
- Wenn der Minuend doch kleiner ist als der Subtrahend, dann können die Vorzeichen zum Rechnen vertauscht werden. Der Subtrahend wird so zum Minuend (oben geschrieben) und der Minuend zum Subtrahend (unten geschrieben). Es kann dann mit den unten beschriebenen Verfahren gerechnet werden. Das Ergebnis muss aber zum Schluss mit einem Minus versehen werden, denn es ist immer negativ (keine natürliche Zahl). Damit wird der zuvor zum Berechnen durchgeführte Vorzeichenwechsel wieder rückgängig gemacht.
- Wenn die einzelnen Stellen der Subtrahenden größer sind als die gleichen Stellen der Minuenden, müssen Überträge gehandhabt werden. Das heißt, der Minuend wird, um die Subtraktion zu ermöglichen, um 10 erhöht; um dies auszugleichen, muss in der links benachbarten Spalte entweder der Minuend erniedrigt (Entbündelungsverfahren; Vorabberechnung der Überträge) oder der Subtrahend erhöht werden (Ergänzungsverfahren; Subtraktion von rechts nach links). Im deutschsprachigen Raum hat sich mit dem Ergänzungsverfahren die letztgenannte Vorgehensweise durchgesetzt. Im Jahr 2000 trat in einigen Bundesländern ein neuer Lehrplan in Kraft, der nun statt des Ergänzens das Entbündeln als Standard vorschreibt.
MMMM
- Schriftliche Subtraktion
- ---
- Ergänzungsverfahren:
- Beim Ergänzungsverfahren, das auch Auffülltechnik oder (in den USA) Austrian method („Österreichische Methode“) genannt wird, wird keine Subtraktion vorgenommen, sondern der Subtrahend umgekehrt bis zum Minuenden erhöht. Falls dies nicht möglich ist, wird der Minuend um 10 erhöht. Die 10 wird nicht „geborgt“, sondern als 1 zum Subtrahenden der nächsten Teilberechnung addiert. Im deutschsprachigen Raum wird dieses Verfahren an den Grundschulen als Standardmethode gelehrt. Einer der Vorteile des Verfahrens besteht darin, dass es den Umgang mit Aufgaben vorbereitet, bei denen von einem Minuenden mehrere Subtrahenden abgezogen werden sollen.
- Beispiel
| Beschreibung | |
|---|---|
| 1 + … = 3 | |
| Das Ergebnis wird unter den Strich geschrieben. | |
| 9 + … = 5 Die angepeilte Summe (5) ist zu klein! | |
| Sie wird darum um 10 erhöht. Die 1 wird unter den nächsten Subtrahenden geschrieben. | |
| 9 + … = 15 Die Berechnung kann jetzt durchgeführt werden, das Ergebnis wird unter den Strich geschrieben. | |
| (4 + 1) + … = 7 | |
| Das Ergebnis wird unter den Strich geschrieben. | |
| Das Gesamtergebnis. |
MMMM
- Schriftliche Multiplikation
- ---
- Schriftliche Multiplikation ist ein Rechenverfahren (Algorithmus), mithilfe dessen eine Multiplikation zweier mehrstelliger Zahlen durch eine schriftliche Darstellung ausgeführt werden kann. Im Folgenden wird das Verfahren für natürliche Zahlen beschrieben. Die Erweiterung auf reelle Zahlen mit endlicher Anzahl an Dezimalstellen erfolgt anschließend.
- ---
- Beispiel:
- Als Beispiel nehmen wir die Zahlen und . Dann ergibt das die Teilschritte
- also
- Mit Hilfe einer versetzten Platzierung der Werte auf bevorzugt kariertem Papier kann man das Notieren der Zehnerpotenzen (in den Grafiken rot dargestellt) einsparen. Unter Verwendung des kleinen Einmaleins und Addition erhält man für die Zeilen:

- Das ganze Schema mit verkürzter Notation der Zeilen ist dann:

- Damit ist die Multiplikation vollständig durchgeführt.
MMMM
- Schriftliche Division
- ---
- Beispiel:
- 12 : 4 = 3
- Dividend : Divisor = Quotient
- ---
- Division natürliches Zahlen:
- Beispiel: Dividiere 1066442 durch 13. Die Division geht auf.
- Schreibe die Aufgabenstellung als Zeile an.
1 0 6 6 4 4 2 : 1 3 =
- Überlege, welche der ersten Ziffern eine Zahl bilden, die groß genug ist, geteilt zu werden: Hier ist dies 106:
1 0 6 6 4 4 2 : 1 3 =
- Dividiere die gefundene Zahl und schreibe das Ergebnis ohne Rest nach dem Gleichheitszeichen. Multipliziere das Ergebnis mit dem Divisor, schreibe es unter die dividierte Zahl. Bilde den Rest durch die Differenz:
1 0 6 6 4 4 2 : 1 3 = 8 1 0 4 _ _ _ 2
- Hole nun die nächste Ziffer von oben:
1 0 6 6 4 4 2 : 1 3 = 8 1 0 4 _ _ _ 2 6
- Dividiere die neue Zahl und wiederhole das Anschreiben des Ergebnisses und der Restdifferenz:
1 0 6 6 4 4 2 : 1 3 = 8 2 1 0 4 _ _ _ 2 6 2 6 _ _ 0
- Hole wieder die nächste Ziffer von oben:
1 0 6 6 4 4 2 : 1 3 = 8 2 1 0 4 _ _ _ 2 6 2 6 _ _ 0 4
- Da in diesem Falle die Zahl nicht geteilt werden kann, weil sie zu klein ist, schreibe als Ergebnis eine 0 auf:
1 0 6 6 4 4 2 : 1 3 = 8 2 0 1 0 4 _ _ _ 2 6 2 6 _ _ 0 4
- Hole die nächste Ziffer von oben und wiederhole die oben genannten Schritte so lange, bis am Ende eine Null als verbleibende Differenz übrigbleibt, und keine Ziffern mehr von oben geholt werden können.
1 0 6 6 4 4 2 : 1 3 = 8 2 0 1 0 4 _ _ _ 2 6 2 6 _ _ 0 4 4
1 0 6 6 4 4 2 : 1 3 = 8 2 0 3 1 0 4 _ _ _ 2 6 2 6 _ _ 0 4 4 3 9 _ _ 5
1 0 6 6 4 4 2 : 1 3 = 8 2 0 3 4 1 0 4 _ _ _ 2 6 2 6 _ _ 0 4 4 3 9 _ _ 5 2 5 2 _ _ 0
MMMM

- Division mit Rest
- ---
- Wir teilen 351 durch 4.
- 351 ist der Dividend, 4 ist der Divisor.
351 : 4 =
- Wir beginnen von links aus zu suchen, welchen möglichst kurzen Abschnitt des Dividenden wir durch den Divisor teilen können.
- Drei lässt sich nicht durch 4 teilen. Der erste Abschnitt, den wir durch 4 teilen können, sind die Ziffern 35 ganz links.
- 35 durch 4 ist 8, denn 8 mal 4 ist 32, und es bleibt der Rest 35 − 32 = 3.
351 : 4 = 8 32 -- 3
- Nun ziehen wir die nächste Ziffer des Dividenden, die 1, zum Rest hinunter, das ergibt 31.
- Jetzt wird die 31 durch 4 geteilt.
- Das ergibt 7, denn 7 mal 4 ist 28, und es bleibt der Rest 31 − 28 = 3.
351 : 4 = 87 32 -- 31 28 -- 3
- Alle Ziffern des Dividenden sind nun verarbeitet. Wir sind fertig:
351 : 4 = 87 Rest 3 32 -- 31 28 -- 3
MMMM
- Division mit mehrstelligem Divisor:
- ---
- Ist der Divisor größer als 10, so reicht das kleine Einmaleins nicht aus, um die jeweils nächste Stelle des Ergebnisses zu bestimmen. Wir finden den passenden Zahlenwert durch Schätzen und Probieren:
13063:32 = … -- 1:32 und 13:32 "gehen" nicht. 130:32 ist sicher mehr als 3:
13063:32 = 3… -- 3·32 rechnen wir im Kopf: 96 -- 34 -- der Rest ist 34 und damit größer als der Divisor; also geht 32 sogar 4-mal in 130!
- Wir haben also zu niedrig geschätzt, streichen die letzten beiden Zeilen und beginnen neu:
13063:32 = 4… -- 4·32 rechnen wir im Kopf oder wie bei der schriftlichen Multiplikation: 4·2=8; 4·3=12; 128 --- 26 -- der Rest ist 2; die "heruntergeholte" 6 gibt 26; 26:32 "geht" nicht; wir schreiben im Ergebnis eine Null an:
13063:32 = 40…
- Nun können wir noch "0·32=0" rechnen und die Rechnung so fortführen:
26 0 -- 26
- Der geübte Rechner sieht aber, dass sich an der 26 nichts ändert, und holt - nachdem er die 0 angeschrieben hat! - sofort die 3 herunter:
13063:32 = 40… 128 --- 263 -- 263:32 schätzen wir auf ungefähr 8. Wir rechnen 8·2=16, Merkzahl 1, 8·3=24, 24+1=25; also: 256 256
- Es bleibt ein Rest von 7, und die fertige Rechnung sieht so aus:
13063:32 = 408 Rest 7
128
---
263
256
---
7
- - oder , oder 13.063 = 32·408+7, wie oben erläutert.
M177
- Division mit Nachkommastelle
- ---
- Wenn wir anstatt einer ganzen Zahl und eines Restes als Ergebnis lieber einen Dezimalbruch haben wollen, schreiben wir hinter das bisherige Resultat ein Komma und rechnen einfach weiter wie bisher, wobei wir an den jeweils letzten Rest immer eine Null rechts anhängen.
950 : 4 = 237,5 8 - 15 12 -- 30 28 -- 20 -- hier bleibt ein Rest von 2; es wird aber kein Rest angeschrieben, sondern ein Komma; dann wird eine 0 "heruntergeholt". 20 - 20:4 geht 5-mal… -- 0 -- …und zwar ohne Rest, deshalb ist die Rechnung hier zu Ende.
MMMM
- Division von Dezimalzahlen
- ---
- Ist der Dividend eine Dezimalzahl (und der Divisor eine natürliche Zahl), so wird zunächst geprüft, ob sein ganzzahliger Teil sich durch den Divisor teilen lässt. Ist dies der Fall, so dividiert man zunächst wie gewohnt. Sobald vom Dividenden eine Ziffer hinter dem Komma „herunterzuholen“ ist, wird im Ergebnis ein Komma gesetzt.
- Ist der ganzzahlige Teil des Dividenden kleiner als der Divisor, so wird im Ergebnis eine Null angeschrieben und dahinter ein Komma. Dann werden die Nachkommastellen des Dividenden (eine nach der anderen!) „heruntergeholt“. Sooft das Ergebnis kleiner bleibt als der Divisor, wird eine weitere Null im Ergebnis angefügt. Danach verläuft die Rechnung wie oben beschrieben.
- Beispiel:
1,8:5 = ?? ----- 1:5 „geht nicht“ - also: „0,...“ anschreiben und eine Nachkommastelle „herunterholen“: 1,8:5 = 0,?? ----- 18:5 „geht“, und zwar 3-mal: 1 8
1,8:5 = 0,3? ----- Der „Rest“ ist 3 — eine „unsichtbare“ 0 wird „heruntergeholt“. 1 5 --- 30 ----- 30:5 „geht“ 6-mal, und zwar ohne Rest; deshalb ist die Rechnung jetzt zu Ende:
1,8:5 = 0,36 1 5 --- 30 30 -- 0
- Ist (auch) der Divisor eine Dezimalzahl, so muss zunächst das Komma verschoben werden, und zwar
- so, dass der Divisor eine ganze Zahl wird,
- gleichsinnig — das heißt in diesem Falle beim Dividenden und beim Divisor nach rechts, und
- um gleich viele Stellen.
- Hat der Dividend weniger Nachkommastellen als der Divisor, so müssen beim Dividenden entsprechend viele Nullen angefügt werden.
- Danach wird dividiert, wie oben beschrieben.
4 : 1,6 = 40 : 16 = 2,5 32 -- 80 80 -- 0
MMMM
- Mengenoperationen
- Operationen mit Mengen
- ---
- Mann kann aus den Mengen M1 und M2 eine neue Menge bilden, die Vereinigungsmenge von M1 und M2. Man schreibt dafür:
- ---
- Allgemein gilt:
- Die Vereinigungsmenge der Mengen A und B besteht aus allen Elementen, die Elemente von A oder Element von B sind.
- Man verwendet für „oder“ das Symbol ∧. Deshalb kann man kürzer schreiben:
- .
- Diesen Zusammenhang kann man graphisch durch drei Mengendiagramm darstellen:

Vereinigungsmenge zweier Mengen
- Man erkennt am unteren Mengendiagramm die mathematische Bedeutung des Wortes „oder“.
- „ oder “ ist wahr für:
- 1. und
- 2. und
- 3. und
- ---
- Allgemein gilt:
- „H1 oder H2“ ist wahr, wenn mindestens eine der Aussagen wahr ist.
- Beachten Sie, dass „H1 oder H2“ auch wahr ist, wenn H1 wahr ist und wenn H2 wahr ist.
- Man kann auch nach den gemeinsamen Elementen von M1 und M2 fragen. Diese Elemente bilden auch eine Menge. Es ist die Durchschnittsmenge der Mengen M1 und M2. Man schreibt dafür
- ---
- Begriff aus der Mengelehre:
- Allgemein gilt:
- Die Durchschnittsmenge von A und B besteht aus allen Elementen, die Element von A und Element von B sind.
- Mit anderen Worten: Wenn , so ist und .
- .
MMMM
- M1 = {9; 10}
- M2 = {0; 22; 27}
- ---
- Betrachten Sie die Mengen M1 und M2! Die Durchschnittsmenge von M1 und M2 ist eine Menge, die aus keinen Elementen besteht. Diese Menge heißt die leere Menge. Men benutzt für sie das Symbol „∅“ oder „“.
- ---
- Allgemein gilt:
- Die leere Menge ist eine Teilmenge von jeder Menge A.
- .
- ---
- Beachten Sie: {0} ≠ ∅
- Jede Menge A hat also mindestens zwei Teilmengen: die Menge A selbst und die leere Menge. Diese beiden Mengen nennt man auch die trivialen Teilmengen der Menge A.
- Man kann noch die Differenzmenge von zwei Mengen A und B bilden. Man schreibt dafür: A\B. Man liest: „Die Differenzmenge von A und B“.
- Die Differenzmenge A\B besteht aus allen Elementen, die Element von A und kein Element von B sind.
- .
- .
- Beispiele:
- M1 = {4; 5; 6}
- M2 = {7; 8; 9; 10}
- M3 = {4; 5; 6; 7; 8}
- M4 = {9; 10}
- M3 \ M1 = {7; 8}
- M1 \ M4 = {4; 5; 6}
- M4 \ M2 = ∅
MMMM
- Negation
- ---
- In der formalen Logik versteht man unter Negation üblicherweise die Satzverneinung, also eine Operation, durch die der Wahrheitswert einer Aussage (eines Satzes) in sein Gegenteil gekehrt wird; auch hier kann mit der Bezeichnung „Negation“ der sprachliche Ausdruck der Verneinung (zum Beispiel das Negationszeichen „¬“ oder die Formulierung „es ist nicht der Fall, dass …“) gemeint sein.
- ---
- In der klassischen Logik, in der genau zwei Wahrheitswerte wahr und falsch – betrachtet werden, ist die Negation unmittelbar als Umkehrung des Wahrheitswertes in sein Gegenteil fassbar: Wenn man eine wahre Aussage verneint, dann entsteht eine falsche Aussage; verneint man hingegen eine falsche Aussage, so entsteht eine wahre Aussage.
- ---
- Gebräuchliche Schreibweisen für die Negation einer Aussage a sind , , und .
- ---
- In der klassischen Logik hat die Negation unter anderem folgende Eigenschaften:
- Die doppelte Verneinung einer Aussage hat stets denselben Wahrheitswert wie die unverneinte Aussage, das heißt Aussagen der Form und sind stets äquivalent (Prinzip der doppelten Negation).
- Eine Aussage der Form ist stets wahr beziehungsweise gültig („Satz vom ausgeschlossenen Dritten“).
- Eine Aussage der Form ist stets falsch beziehungsweise ungültig („Satz vom Widerspruch“).
MMMM
- Wie viel Elemente hat die Menge B = {4; 5; 6; 7; 8}?
- Warum ist A = {9; 10} eine endliche Menge?
- Unter welchen Bedingungen sind zwei Mengen gleich?
- Was für eine Menge ist die Menge der natürlichen Zahlen?
- Unter welchen Bedingungen sit die Menge C eine Teilmenge der Menge D?
- Kann eine unendlichen Menge eine unendlichen Teilmenge haben?
- ---
- Kann eine endlichen Menge eine unendlichen Teilmenge haben?
- Wie liest man den Ausdruck: „“?
- Wie liest man: „“ und „“?
- Was für Zahlen sind 2n und 2n+1, wenn n ∈ ℕ?
- Wie liest man: „“ und „“?
- Wie ist die Vereinigungsmenge der Mengen K und P erklärt?
- ---
- Unter welchen 3 Bedingungen ist „“ wahr?
- Wie ist die Durchschnittsmenge der Mengen M und N erklärt?
- Was versteht man unter der leeren Menge?
- Welche trivialen Teilmengen hat jede Menge M?
- Aus welchen Elementen besteht die Differenzmenge M \ N der Mengen M und N?
- Wie liest man „“?
- Ist 6,3 eine gerade oder eine ungerade Zahl?
MMMM
- Lesen Sie!
- ---
- Beispiel
- a) „“ und „“
- (a ist ein Element aus N, und b und c sind keine Elemente aus M.)
- ---
- b) „“ und „“
- c) „“, aber „“
- d) „“ und „“
- d) „“ und „“
- ---
- C = {4; 5; 6; 7}
- D = {7; 8; 9; 10}
- „“, aber „“
MMMM
- N = {0; 1; 2; 3; 4; ... ; n; ...}
- Die Menge N hat unendlich viele Elemente.
- Die Menge N besteht aus unendlich vielen Elementen.
- ---
- Nu = {1; 3; 5; 7; ... ; 2n+1; ...}
- Die Menge Nu hat unendlich viele Elemente. (u steht für ungerade Zahlen)
- ---
- S = {2; 4; 6; 8; 10; 12; ...}
- T = {2; 4; 6; 8; 10; 12}
- Die Menge S hat endlich viele Elemente.
- Die Menge S hat 6 Elemente.
MMMM
- Lesen Sie!
- ---
- Beispiel:
- Für alle Element x aus Ng gilt, dass x ein Element aus ℕ ist.
- Für jedes Element x aus Ng gilt, dass x ein Element aus ℕ ist.
- ---
MMMM
- wenn ..., so ...
- ---
- Lesen Sie!
- ---
- Wenn A eine Teilmenge von B ist und wenn B eine Teilmenge von C ist, so ist A eine Teilmenge von C.
- ---
MMMM
- es gibt mindestens ein ..., so dass ...
- ---
- Lesen Sie!
- ---
- Es gibt mindestens ein Element x in N, so dass x ein Element Ng ist.
- ---
MMMM
- Teilmenge
- echte Teilmenge
- ---
- A = {1; 2; 3; 4}; B = {1; 2; 3}
- Die Menge B ist eine echte Teilmenge der Menge A.
- ---
- C = {6; 14}; D = {6; 14}
- Die Menge D ist eine echte Teilmenge der Menge C.
MMMM
- Bilden Sie aus den gegebenen Mengen die Vereinigungsmenge, die Durchschnittsmenge und die Differenzmenge!
- ---
- A = {1; 2; 3; 4}; B = {5; 6; 7}
- ---
- M = {3; 4; 7}; N = {3; 4; 8}
- R = {4; 5; 6}; S = {4; 5; 6}
- P = ∅; T = {1; 2; 3}
- K = {1; 2; 3; 4; 5}; L = {3; 4}
- C = {4; 5; 6; 7; 8}; F = {7; 8; 9; 10}
- ---
- Betrachten Sie außerdem für die Mengen C und F die Elemente 4; 5; 7 und 9!
- ,
- ,
- ,
- .
MMMM
- Scheiben Sie die folgenden Ausdrücke in Worten, und zeichnen Sie die Mengendiagramme!
- Prüfen Sie die Wahrheit der Aussagen!
- ---
- Beispiel:
- (wahr)
- Wenn die Durchschnittsmenge von A und B die leere Menge ist, so gibt es kein Element x aus A, so dass x ein Element aus B ist (wahr)
- ---
- Beispiel:
- (falsch)
- Wenn für alle Elemente x aus A gilt, dass x ein Element aus B ist, so ist A eine echte Teilmenge von B. (falsch)
- ---
- 1.)
- 2.)
- 3.)
- 4.)
- 5.)
- 6.)
- 7.)
- 8.)
- 9.)
- 10.)
- 11.)
- 12.)
- 13.)
- 14.)
Lösung ???
MMMM
- Wenn die Ausagen der Übung M193 falsch sind, dann korrigieren Sie die rechten Seiten der Aussagen, so dass wahre Aussagen entstehen!
- ---
- Beispiel:
- (falsch)
- (wahr)
Lösung ???
MMMM
- Die Bedeutung des Wortes „oder“ in der Mathematik.
- ---
- A = {0; 1; 2; 3}; B = {2; 3; 4; 5;6}
- ---
- Beispiel:
- Ist der Ausdruck wahr?
- oder
- „ oder “ ist wahr, weil „“.
- ---
- 1.) oder
- 2.) oder
- 3.) oder
- 4.) oder
- 5.) oder
- 6.) oder
- 7.) oder
- 8.) oder
- 9.) oder
- 10.) oder
MMMM
- Klammerregeln
- ---
- Klammerregeln im engeren Sinn
- Für das Auflösen von Klammern in Summen und Differenzen gilt:
- Steht ein Pluszeichen vor der Klammer, so kann man die Klammer einfach weglassen.
- Steht ein Minuszeichen vor der Klammer, so wird die Klammer und das Minuszeichen weggelassen und es werden die Vor- und Rechenzeichen innerhalb der Klammer umgekehrt.
- Beispiele
- Klammerregeln im weiteren Sinn
- Treten Klammern in mathematischen Ausdrücken auf, so werden die Operationen (z.B. plus oder mal) innerhalb der Klammern immer vor denjenigen außerhalb der Klammern ausgeführt.
- Beispiel 1
- (2 + 5) · 3 = 7 · 3 = 21, (erst das "+", dann das "·" wegen der Klammern), aber
- 2 + 5 · 3 = 2 + 15 = 17, (Punkt- vor Strichrechnung).
- Beispiel 2
- (2 · 3)² = 6² = 36, aber
- 2 · 3² = 2 · 9 = 18.
MMMM

- Rechenregeln
- ---
- Im Folgenden sind , und Zahlen aus dem zugrundeliegenden Zahlbereich. Für die Addition und die Multiplikation gelten die Kommutativgesetze
- und ,
- das heißt das Ergebnis einer Summe oder eines Produkts ist unabhängig von der Reihenfolge der Summanden bzw. Faktoren. Weiter gelten die Assoziativgesetze
- und .
- Bei der Addition oder der Multiplikation mehrerer Zahlen ist es also unerheblich, in welcher Reihenfolge die Teilsummen oder Teilprodukte gebildet werden. Daher können bei Summen und Produkten die Klammern auch weggelassen werden. Zudem gelten die Distributivgesetze
- und ,
- mit denen durch Ausmultiplizieren ein Produkt in eine Summe umgewandelt werden kann und umgekehrt durch Ausklammern eine Summe in ein Produkt. Weiterhin verhält sich die Zahl neutral bezüglich der Addition und die Zahl neutral bezüglich der Multiplikation, das heißt
- und .
- Für die Subtraktion und die Division gelten diese Gesetze nicht oder nur eingeschränkt. Weitere Rechenregeln, wie Punkt vor Strich, die Klammerregeln und die Gesetze der Bruchrechnung, finden sich in der Formelsammlung Arithmetik.
MMMM
- Übersetzen Sie den Artikel ins Deutsche!
- ---
- Radicación
- ---
- La radicación es el proceso opuesto a la potenciación. Es decir, matemáticamente:
- En el proceso de radicación, buscamos un B que satisfaga la condición anterior.
- ---
- Método de resolución para raíces cuadrada:
- El método más difundido para su resolución, es el siguiente:
- Tomemos como ejemplo, el radicando 65536.
- El primer paso es la separación en grupos de dos del radicando, así: Ahora se busca un número que multiplicado por sí mismo sea lo más próximo (por defecto) al primer grupo de números, comenzando por la izquierda.
- Si el número no es un entero, los grupos se realizarán a partir de la coma decimal, hacia ambos lados. Si el número posee una cantidad impar de cifras decimales, se agrega un cero a la derecha, por ejemplo en el caso 123,456 la separación sería 1.23,45.60. Al llegar a la parte decimal, se pondría también en ese mismo paso la coma en el resultado.
- En este caso es el 2, pues 22=4 < 6 . Este número se resta del grupo de dígitos del radicando, y a la diferencia se le concatena el siguiente grupo. Es decir,
fuente: Vikidia - Vikidia - La enciclopedia libre de contenido adaptado para niños y jóvenes que todos pueden editar)
- fuente/Quelle: Vikidia:Radicación
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
- licence: CC BY-SA 3.0 (english)
MMMM
- Übersetzen Sie ins Deutsche!
- ---
- Geometría
- ---
- La geometría es una parte de la matemática que se ocupa del estudio de las figuras en el plano o en el espacio, incluyendo: puntos, líneas, planos,superficies, polígonos, poliedros, etc.
- Sus orígenes se remontan a la solución de problemas de medidas. Es una de las ciencias más antiguas. En el Antiguo Egipto estaba muy desarrollada. Euclides, en el siglo III a. C. fue el creador de la geometría euclidiana descrita en el libro «Los Elementos».
- La geometría tiene su aplicación práctica en física, arquitectura, geografía, astronomía, etc.
- ---
- Cuadrado:
- Cuadrado es un polígono regular. Tiene los cuatro lados iguales y los cuatro ángulos son rectos.
- Las diagonales del cuadrado son perpendiculares entre si e iguales y son bisectrices de los ángulos.
- Área del cuadrado : el área del cuadrado es igual al lado del cuadrado multiplicado por si mismo. La formula del área del cuadrado es: l*l (lado por lado)
- Perímetro del cuadrado : el perímetro del cuadrado es igual al lado del cuadrado multiplicado por 4 (cuatro). La fórmula del perímetro del cuadrado es: l*4 o l+l+l+l (lado por 4 cuatro) o ( lado más lado más lado más lado )
- ---
- Rectángulo:
- Rectángulo es un paralelogramo que tiene los lados contiguos desiguales y los cuatro ángulos rectos.
- En un rectángulo los diagonales son iguales.
- Área del rectángulo : El área del rectángulo es igual al producto de sus dos dimensiones.
- ---
- Paralelogramo:
- Los paralelogramos tienen los lados iguales dos a dos.
- Los lados opuestos son iguales. Los ángulos opuestos son iguales.
- Los ángulos que tienen un lado común son suplementarios por ser ángulos colaterales internos.
- Las diagonales se cortan en partes iguales.
- La base de un paralelogramo es uno cualquiera de sus lados. La altura es la perpendicular común a la base y al lado opuesto.
- ---
- Rombo:
- Rombo es el paralelogramo que tiene cuatro lados iguales y los ángulos oblicuos.
- Las diagonales del rombo son perpendiculares entre si. Las diagonales son bisectrices de los ángulos.
- Área del rombo : el área del rombo es igual a la mitad del producto de las diagonales (el rombo es la mitad del rectángulo que tiene por dimensiones las diagonales).
-
Cuadrado
-
Rectángulo
-
Paralelogramo
-
Rombo
fuente: Vikidia - Vikidia - La enciclopedia libre de contenido adaptado para niños y jóvenes que todos pueden editar)
- fuente/Quelle: Vikidia:Geometría
- fuente/Quelle: Vikidia:Cuadrado
- fuente/Quelle: Vikidia:Rectángulo
- fuente/Quelle: Vikidia:Paralelogramo
- fuente/Quelle: Vikidia:Rombo
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
- licence: CC BY-SA 3.0 (english)
MMMM
- Übersetzen Sie ins Deutsche!
- ---

El diámetro es la línea azul y la circunferencia el borde negro. La relación matemática entre ellós es el número pi. - Número pi
- ---
- El número pi o número π es un número que representa la relación entre el ancho de un círculo, llamado diámetro, y lo que mide su borde exterior, llamado circunferencia.
- Así pues, si el diámetro de un círculo mide de ancho 1, su circunferencia medirá π de largo; y si mide 5 de ancho, su circunferencia medirá 5 veces π de largo. El número pi es el mismo para todos los círculos, por lo que se dice que es una constante. El número pi es un poco más grande que tres:
- ---
- π = 3,1415926535897932.....
- ---
- El número pi es un número infinitamente grande, no tiene fin, ya que es un número irracional. Es tan grande que se pueden buscar otros números dentro de él, como un número de teléfono, y que los ordenadores más grandes pueden calcular muchísimas de sus cifras sin llegar al final, por que nunca acaba.

Si el circulo tiene de ancho 1, al desenrrollar su borde acaba midiendo el número pi, que es un poco más de 3. Si fuese un círculo el doble de ancho, la longitud del borde sería el doble también.
fuente: Vikidia - Vikidia - La enciclopedia libre de contenido adaptado para niños y jóvenes que todos pueden editar)
- fuente/Quelle: pi Vikidia:Número pi
- licencia: CC-BY-SA (español)
- Lizenz: CC-BY-SA (deutsch)
- licence: CC BY-SA 3.0 (english)
MMMM
- ---
- Was ist eine Menge?
- ---
- Der Begriff „Menge“ ist in der Mathematik grundlegend. Wir haben ein natürliches, intuitiv richtiges Verständnis für Mengen.
- ---
- Intuition (von mittellateinisch intuitio = unmittelbare Anschauung, zu lateinisch intueri = genau hinsehen) ist die Fähigkeit, Einsichten in Sachverhalte oder Gesetzmäßigkeiten zu erlangen, ohne ohne bewusste Schlussfolgerungen. Intuition ist ein Teil kreativer Entwicklungen. Der die Entwicklung begleitende Intellekt führt nur noch aus oder prüft bewusst die Ergebnisse, die aus dem Unbewussten kommen. Kritisch ist hierbei zu sehen, dass bei positiver Wirkung einer Entscheidung gerne von Intuition gesprochen wird, während man im Falle des Scheiterns schlicht „einen Fehler gemacht“ hat, wobei es gerade keinen Mechanismus gibt zu prüfen, welche mentalen Vorgänge zur jeweiligen Entscheidung führten.
- ---
- Definition der Menge:
- Eine Menge ist ein Verbund, eine Zusammenfassung von einzelnen Elementen.
- ---
- Bei der Beschreibung einer Menge geht es ausschließlich um die Frage, welche Elemente in ihr enthalten sind. Es wird nicht danach gefragt, ob ein Element mehrmals enthalten ist oder ob es eine Reihenfolge unter den Elementen gibt. Eine Menge muss kein Element enthalten - es gibt genau eine Menge ohne Elemente, die „leere Menge“.
- Es existiert keine Definition im strengen Sinn für „Mengen“. Jeder Versuch einer Definition schließt unvermeidlich die Verwendung des Wortes „Menge“ oder eines anderen Wortes ähnlicher Bedeutung. Eine analoge Situation ergibt sich für den Begriff „Farbe“.
- Um ein Verständnis für den Begriff der „Menge“ zu erlangen, können wir ihn in Bezug zu unseren bestehenden Erfahrungen setzen. Eine Menge kann man sich als Gefäß vorstellen, als Schachtel, Beutel oder Sack, der Gegenstände enthält - das sind die Elemente der Menge. Diese Schachtel ist sozusagen ein Modell für unser Menge.
MMMM
- In der Mathematik sind die Elemente einer Menge häufig Zahlen oder Punkte, das Konzept ist jedoch auf beliebige Objekte anwendbar: z. B. in der Statistik Stichproben, in der Medizin Patientenakten, am Marktstand eine Tüte Früchte.
- ---
- Eine Veranschaulichung des Mengenbegriffs, die Richard Dedekind zugeschrieben wird, ist das Bild eines Sackes, der gewisse (als Einzelne abgrenzbare) Dinge enthält. Nützlich ist diese Vorstellung zum Beispiel für die leere Menge: ein leerer Sack. Die leere Menge ist also nicht „nichts“, sondern der Inhalt eines Behältnisses, das keine der für es als Inhalt vorgesehenen Dinge enthält. Das „Behältnis“ selbst verweist nur auf die bestimmte zu zählende Sorte und Art von Elementen. Diese Vorstellung hat aber ihre Grenzen. Ein Behältnis bleibt nämlich dasselbe, auch wenn man seinen Inhalt ändert. Dies ist bei Mengen anders: Diese ändern ihre Identität, wenn man neue Elemente hinzufügt oder bestehende entfernt. Insofern ist es besser, wenn man sich die Menge als „Inhalt eines Behältnisses“ vorstellt.
MMMM
- naive Mengenlehre
- ---
- Der Begriff der naiven Mengenlehre entstand am Anfang des 20. Jahrhunderts für die Mengenlehre des 19. Jahrhunderts, in der eine ungeregelte oder unbeschränkte Mengenbildung praktiziert wurde.[1] Wegen Widersprüchen, die sich in ihr ergeben, wurde sie später abgelöst durch die axiomatische Mengenlehre, in der die Mengenbildung über Axiome geregelt wird. „Naive Mengenlehre“ bezeichnet daher primär diese frühe Form der ungeregelten Mengenlehre und ist als Kontrastbegriff zur axiomatischen Mengenlehre zu verstehen.
- ---
- Problematik
- Für die Intention der unbeschränkten naiven Mengenbildung wird oft die Mengendefinition von Georg Cantor zitiert: Unter einer „Menge“ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche die „Elemente“ von M genannt werden) zu einem Ganzen. Bei genauer Betrachtung ist dies aber nicht stichhaltig (siehe unten). Eine Mengenlehre mit einer unbeschränkten Mengenbildung findet man aber bei anderen Mathematikern des ausgehenden 19. Jahrhunderts: bei Richard Dedekind und Gottlob Frege. Sie ist daher durchaus typisch für die frühe Mengenlehre. Aus der Sicht der Mathematiker des 20. Jahrhunderts wurde sie als naive Mengenlehre bezeichnet, da sie bei gewissen extremen Mengenbildungen zu Widersprüchen führt. Bekannte Antinomien, die auch als logische Paradoxien bezeichnet werden, sind in der naiven Mengenlehre zum Beispiel die folgenden:
- Die Menge aller Ordinalzahlen führt zum Burali-Forti-Paradoxon von 1897 (erste publizierte Antinomie).
- Die Menge aller Kardinalzahlen erzeugt die erste Cantorsche Antinomie von 1897.
- Die Menge aller Dinge oder Mengen erzeugt die zweite Cantorsche Antinomie von 1899.
- Die Menge aller Mengen, die sich nicht selbst als Elemente enthalten, ergibt die Russellsche Antinomie von 1902.
MMMM
- Ordinalzahl
- Ordinalzahlen sind mathematische Objekte, die das Konzept der Position oder des Index eines Elementes in einer Folge auf Wohlordnungen über beliebigen Mengen verallgemeinern. Positionen in Folgen werden als natürliche Zahlen aufgefasst (sprachlich durch die Ordinalia erstes, zweites, drittes, ... Element ausgedrückt), welche die endlichen Ordinalzahlen bilden.
- Die Beschreibung der Größe einer Menge, naiv gesprochen der Anzahl ihrer Elemente, führt im Gegensatz dazu zu dem Begriff Kardinalzahl (eins, zwei, drei, ...).
- ---
- Kardinalzahl
- Kardinalzahlen (lat. cardo „Türangel“, „Dreh- und Angelpunkt“) sind in der Mathematik eine Verallgemeinerung der natürlichen Zahlen zur Beschreibung der Mächtigkeit, auch Kardinalität, von Mengen.
- Die Mächtigkeit einer endlichen Menge ist eine natürliche Zahl – die Anzahl der Elemente in der Menge.
- ---
- axiomatische Mengenlehre
- Als axiomatische Mengenlehre gilt jede Axiomatisierung der Mengenlehre, die die bekannten Antinomien der naiven Mengenlehre vermeidet.
MMMM
- Enthaltensein in einer Menge
- ---
- Eine Menge kann über ein Verfahren definiert weden, mit dem ermittelt wird, ob irgendein gegebenes objekt ein Element dieser Menge ist oder nicht.
- Man sagt: „die Menge enthält das Objekt“.
- ---
- Ein Verfahren zur Bestimmung, ob ein Element zu einer bestimmten Menge zählt, ist manchmal mehr als eine schlichte Beschreibung. WEnn weir beispielsweise versuchen von der Menge der „hohen Häuser“ zu sprechen, so reicht es nicht einfach die Beschreibung „hoch“ und „Haus“ zu verwenden. Weir müssen genau angeben wie wir zwischen „hoch“ und „nicht hoch“ unterscheiden und zwischen „Haus“ und „Bauwerk“. Um eindeutige Antworten für Grenzfälle zu erhalten brauchen wir exakte mathematische Formulierungen.
- ---
- Notation zur Darstellung des Enthaltenseins in Mengen
- Die Dinge, die in einer Menge enthalten sind, heißen Elemente. Ist ein Objekt Element einer Menge , so schreibt man dafür formal: . Die Verneinung ( ist kein Element von ) schreibt man als: .
- ---
- Eine Menge ist durch ein genau definiertes Kriterium definiert, das uns in die Lage versetzt zu entscheiden, ob irgendein gegebenes Objekt Element dieser Menge ist.
- ---
- Eine andere Möglichkeit zur Beschreibug einer Menge ist eine Mengenaufzählung. Das ist eine explizite Liste mit allen Elementen der Menge.
- Bei der Entscheidung ob ein Element zur Menge gehört, muss man also nur jedes einzelne Element der Aufzählungsliste durchgehen bis eine Übereinstimmung gefunden wird oder auch nicht gefunden wird.
- Die Mengenaufzählung besteht aus einer List in geschweiften Klammern.
- Beispiel:
- F = {rot, grün, blau, schwarz}
MMMM
???
- Mengenrelationen
- Mengenrelationen geben an, wie sich zwei Mengen zueinander „verhalten“ oder eben „in Relation stehen“.
weiter mit Mengenlehre - dann Geometrie ???


















































































































































































![{\displaystyle B^{C}=A\Longleftrightarrow {\sqrt[{C}]{A}}=B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e94c25c45f8a15bec681da503a8a675336b5a7af)