Curso de alemán para principiantes con audio/Lección 061b

índice

Lección 060b ← Lección 061b → Lección 062b

Lección 061

Mathematik auf Deutsch - 11

BM501 - BM510

BM501

Runden

Es sollen nun mehrere Grundziffern durch Nullen ersetzt werden.

---

Es soll 5.728 auf ein Vielfaches von 1.000 gerundet werden.

In diesem Fall ist die Grundziffer von Interesse, die die Zahl der Vielfachen von 100 angibt. Es handelt sich um eine 7. Also muss aufgerundet werden.

5.728 ≈ 6.000

---

Es soll 5.028 auf ein Vielfaches von 1.000 gerundet werden.

Die Grundziffer für die Anzahl der Vielfachen von 100 ist 0. Also muss abgerundet werden.

5.028 ≈ 5.000

BM502

Besondere Beachtung verdient wieder die 5.

Es soll jeweils auf ein Vielfaches von 1.000 gerundet werden.

---

876.523

Es wird aufgerundet; denn auf 5 folgen noch andere von Null verschiedene Grundziffern.

876.523 ≈ 877.000

---

876.500

Auf 5 folgen nur Nullen. In diesem Fall wird die gerade-Zahl-Regel angewendet. Man rundet ab, da 6 eine gerade Zahl ist.

876.500 ≈ 876.000

---

877.500

Auf 5 folgen nur Nullen. man rundet auf, da 7 eine ungerade Zahl ist.

877.500 ≈ 878.000

BM503

Wiederholung:

Runden

---

Zahlen werden im Alltag oft gerundet, damit wir sie uns einfacher einprägen können - oft will man es ja gar nicht so genau wissen.

Meistens resultieren Zahlen aber aus Messungen oder Rechnungen mit endlicher Genauigkeit, bei denen es irreführend wäre, mehr Ziffern als die Genauigkeit anzugeben. In solchen Fällen ist eine Rundung auf die Genauigkeit der Rechnung oder Messung in jedem Falle notwendig.

Es gibt auch Fälle, wo nur eine bestimmte Anzahl von Nachkommastellen erlaubt ist, etwa kann man Geldbeträge in Euro nur auf ganze Cent herausgeben, Mehrwertsteuern oder Rabatte fallen aber meist in Prozent an. Das Ergebnis ist dann also auf ganze Cent zu runden.

Ähnliches gilt, wenn Geld aus einer Währung in eine andere getauscht werden soll.

BM504

Wiederholung:

Runden

---

Beim Runden wird also zunächst festgestellt (Messung, näherungsweise Rechnung) oder festgelegt, auf wieviele Ziffern gerundet werden soll. Die nach rechts nachfolgenden Ziffern entscheiden dann, wie gerundet wird:

Bei den Ziffern 0,1,2,3 und 4 wird abgerundet.
Bei den Ziffern 6,7,8 und 9 wird aufgerundet.
Bei der Ziffer 5 ist die Regel etwas komplizierter. Folgen weitere Ziffern, von denen eine nicht 0 ist, wird aufgerundet. Ist die 5 hingegen die letzte Ziffer, so wird so gerundet, dass die letzte Ziffer nach dem Runden gerade ist.

---

Das Ergebnis ist so stastisch neutral, das bedeutet, wenn man nach der Regel sehr viele Zahlen rundet, gibt es durch das Runden im Mittel keine Abweichung der Werte nach dem Runden von denen davor. Das würde übrigens auch gelten, wenn man immer so runden würde, dass die letzte Ziffer nach dem fünfer-Runden ungerade ist, was aber nicht üblich ist.

BM505

Wiederholung:

Runden

---

Weil die Regel mit der Ziffer 5 kompliziert ist, runden einige Leute bei der Ziffer 5 immer auf. Das wird auch Kaufmännisches Runden genannt.

Werden so sehr viele Zahlen gerundet, ist der Mittelwert nach dem Runden etwas größer als davor. Bei Geldbeträgen ist das vorteilhaft für den, der das Geld bekommt - vielleicht heißt es deshalb Kaufmännisches Runden ...

---

Oft wird bei Messungen und Rechnungen auch davon gesprochen, auf wieviele gültige Ziffern ('signifikante' Ziffern - ohne vorangehende Nullen) gerundet werden soll, 0,000127 hat also drei signifikante Ziffern.

---

Auch wenn bei einer Rechnung eine Zahl beteiligt ist, die bereits gerundet ist, ist das Endergebnis wieder entsprechend zu runden. Die Zahl der signifikanten Ziffern des Ergebnisses ist also die gleiche wie die der Zahl der Rechnung mit den wenigsten signifikanten Ziffern. In dem Zusammenhang kann es auch wichtig sein, nachfolgende Nullen zu notieren, um anzugeben, wieviele Ziffern signifikant sind, 0,00012700 hat also fünf signifikante Ziffern, 0,0001270 nur vier und 0,000127 nur drei.

---

Beim Runden verwendet man das Zeichen ~, es bedeutet „ungefähr“ gleich.

Beispiele:

gerundet auf	ungerundete Zahl	gerundete Zahl
Zehner	479764	479760
Hunderter	479764	479800
Tausender	479764	480000
Geld/Euro auf Cent	17,125	17,12
Geld/Euro auf Cent	17,135	17,14
Messung, drei signifikante Ziffern	7,285	7,28
Messung, drei signifikante Ziffern	0,00514523531	0,00515
Rechnung 1,20 * 11,1 / 2 + 2,1050	8,7650	9

BM506

Runden

Zusammenfassung:

Gerundete Zahlen sind Näherungswerte.

---

Runden auf ein Vielfaches von 10:

Gerade-Zahl-Regel: Es wird aufgerundet, wenn die Ziffer vor 5 ein ungerade Zahl bezeichnet. Es wird abgerundet, wenn die Ziffer vor 5 eine gerade Zahl bezeichnet.

---

Runden auf ein Vielfaches von 100:

Auf Vielfache von 1.000; 10.000 usw. rundet man entsprechend.

BM507

Strahl

---

Sonnenstrahl
Rad mit Speichen

Ein Strahl bzw. eine Halbgerade ist in der Geometrie - anschaulich gesprochen - eine gerade Linie, die auf einer Seite begrenzt ist, sich aber auf der anderen Seite ins Unendliche erstreckt.

Eine Gerade geht in beide Richtungen ins Unendliche.

---

Bild 1 zeigt einen Zahlenstrahl, auf dem die Zahlen 0, 1, 2, 3... , 7 eingetragen wurden.

Man kann mehr Zahlen eintragen, wenn der Abstand der Punkte verkürzt wird oder wenn ein längeres Stück des Zahlenstrahls gezeichnet wird. (Bild 2)

Die Veranschaulichung von Zahlen an Zahlenstrahlen benutzt man oft zur übersichtlichen Darstellung von Zahlenangaben. (Bild 3)

BM508

Karo: eine der vier Farben im französischen Kartenspielblatt: ♦ (Bild 1)

♦

Der Begriff „Karo“ kam im 18. Jahrhundert über das französische „carreau“ in die deutsche Sprache und geht auf lateinisch quadrum „Viereck, Quadrat“ zurück.

Karo (selten) oder Raute (oder Rhombus), gleichseitiges Parallelogramm, meist auf der Spitze stehend. (Bild 2)

Merkel-Raute (Bild 3 und 4) - Benannt ist die Geste nach der deutschen Bundeskanzlerin Angela Merkel, bei der diese Form der Handhaltung zu einem charakteristischen Teil ihres Auftretens in der Öffentlichkeit geworden ist.

Bild 1
Bild 2
Bild 3
Bild 4

---

kariert = mit Kästchen oder Karos versehen; gewürfelt (der Würfel)

kariert als Musterung (Muster)

ein kariertes Hemd (Bild 5)

ein kariertes Kleid (Bild 5a)

ein gelb-schwarz kariertes Follow-me-Car am Flughafen (Bild 6)

gelb-schwarz karierte Signalflagge in der Schifffahrt (Bild 6)

Bild 5
Bild 5a
Bild 6
Bild 7

---

kariertes Papier (Bild 8 und 9)

Karo (rot markiert - in Bild 8 und 9)

Kariertes Papier hat meist quadratische Karos. Es gibt aber auch kariertes Papier mit rechteckigen Karos.

Für den Mathematikunterricht werden meist karierte Blätter oder Heft mit kariertem Papier bevorzugt.

Liniertes Papier (Bild 10)

Notenpapier (Bild 11)

Millimeterpapier (Bild 12)

Bild 8
Bild 9
Bild 10
Bild 11
Bild 12

BM509

Strecke

Veranschaulichung von Strecken mit Hilfe eines Streckendiagramms. (Bild 1)

---

Säule

Veranschaulichung von Strecken mit Hilfe eines Säulendiagramms. (Bild 2)

Das Säulendiagramm ist ein Diagramm, das durch senkrecht stehende, nicht aneinandergrenzende Säulen (Rechtecke mit bedeutungsloser Breite) die Häufigkeitsverteilung einer Variablen veranschaulicht.

Das Säulendiagramm eignet sich besonders, um wenige Zahlen (bis ca. 15) zu veranschaulichen.

Bei mehr Kategorien leidet die Anschaulichkeit und es sind Liniendiagramme zu bevorzugen.

BM510

Balkendiagramm

Das Balkendiagramm ist einer der häufigsten Diagrammtypen. Es ist dem Säulendiagramm sehr ähnlich, stellt die Datenreihen allerdings durch waagerecht liegende Balken dar. Es eignet sich sehr gut zur Veranschaulichung von Rangfolgen.

Bild 1
Bild 2
Bild 3

---

Ein Diagramm (von altgriechisch „geometrische Figur, Umriss“) ist eine grafische Darstellung von Daten, Sachverhalten oder Informationen. Je nach der Zielsetzung des Diagramms werden höchst unterschiedliche Typen eingesetzt.

BM511 - BM520

BM511

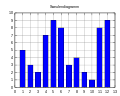
Säulendiagramme

---

Erkläre die verschiedenen Säulendiagramme!

Bild 2: Anzahl der Versicherungsmitglieder, aufgeteilt in Beitragszahler und Rentner in einer Krankenversicherung.

Bild 3: Vergleich der bestellten Flugzeuge bei Boeing und Airbus

Bild 4: Temperaturschwankungen in der Arktis (Abweichungen von einem Mittelwert)

Bild 5: Öffentliche Ausgaben einer japanischen Stadt, die sich aus 4-5 verschiedene Positionen zusammensetzen. (z. B. Kommunalverwaltung, Schule, Polizei, Schwimmbad, Zuschüsse für soziale Einrichtungen usw. usf.)

Bild 6: Verteilung von Männern (blau) und Frauen (rot)

Bild 7: Altersverteilung (Altersgruppen: 0-17 Jahre; 18-24 J., 25-44 J., 45-64, 65+)

Bild 8: Chemiewaffenproduktion (4 Arten chemischer Kampfstoffe; [Sarin, Tabun, Senfgas, VX], Menge in Tonnen, je Jahr)

Bild 9: Warenumschlag im Hamburger Hafen (3 Arten Waren [konventionelles Stückgut, Massengut, Stückgut Container], in Mill. Tonnen, je Jahr)

Bild 10: Ergenisse der Parlamentswahlen in der Ukraine 2007 (6 verschiedene Parteien, rund 30 Provinzen, Stimmenzuwachs bzw. -abnahme)

Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
Bild 6
Bild 7
Bild 8
Bild 9
Bild 10

BM512

Verschieden Typen von Diagrammen:

---

Kreisdiagramm (Bild 1)

Ringdiagramm (Bild 2)

Tortendiagramm = Kuchendiagramm (Bild 3)

Netzdiagramm (Bild 4)

Liniendiagramm (Bild 5)

Punktdiagramm (Bild 6)

Mengendiagramm (Bild 7)

---

Bild 1: Kreisdiagramm
Bild 2: Ringdiagramm
Bild 3: Tortendiagramm
Bild 4: Netzdiagramm
Bild 5: Liniendiagramm
Bild 6: Punktdiagramm
Bild 7: Mengendiagramm

BM513

Hermann warf den Ball 12 m weiter als Jörg. Thorsten schaffte 8 m weniger als Hermann und Bernd 5 m mehr als Hermann.

Wie weit warf Jörg den Ball?

Welches Kind warf den Ball am weitesten?

---

Marlies tauchte 5 s länger unter Wasser als Petra. Gabi sogar 7 s länger. Simone tauchtee 2 s weniger als Gabi.

Wie lange tauchte Petra unter Wasser?

Welches Mädchen tauchte die gleiche Zeit?

---

Rainer hat schon 40 Euro gespart, Lena 5 Euro weniger. Karsten hat 17 Euro mehr als Lena, und karin fehlen noch 2 Euro, dann hat sie 50 Euro gespart.

Wie viel Euro hat jedes Kind?

---

Der Vater ist 35 Jahre alt, Ingrid erst 5. Ihre Schwester Kerstin ist 3 Jahre älter. Ihr Bruder ist 25 Jahre jünger als der Vater.

Wie alt sind Kerstin und ihr Bruder?

Wie alt ist die Mutter?

BM514

Nicht immer kann für ein Streckendiagramm als Einheit die Höhe eines Rechteckkästchens gewählt werden. Hierzu würde oft der Platz nicht reichen.

---

Zeichne ein Streckendiagramm, um folgende Werte zu veranschaulichen:

Uhrzeit	6:00	9:00	12:00	15:00	18:00	21:00
Temperatur	17°C	21°C	26°C	28°C	24°C	19°C

Man könnte für 17°C eine Strecke von 17 mm zeichnen.

Lösung BM514
Hier wurden 4 Kästchen für 10° gewählt. Kariertes Papier hat meist Quadrate von 5 mm Kantenlänge. Also sind 10° gleich 2 cm oder 20 mm. Also entsprechen 10° genau 20 mm. Für 17°C wird also eine Strecke von 34 mm gezeichnet. Wie viel Millimeter sind die anderen Strecken lang? Temperaturmessungen im Tagesverlauf

BM515

Bei der Anfertigung eines Diagramms sind folgende Teilschritte zu beachten.

1.) Suche die kleineste und die größte Zahl, die jeweils dargestellt werden soll!

2.) Runde beide Zahlen und Vielfache derselben Zehnerpotenz!

3.) Lege die Länge der Strecke für die gewählte zehnerpotenz so fest, dass die Darstellung auf dem Zeichenblatt möglich ist.

4.) Zeichen den Strahl, auf dem die Strecken senkrecht stehen sollen, und lege die Anfangspunkte der Strecken fest! Beachte den Platz für die Beschriftung!

5.) Berechne die Streckenlänge und zeichne die Strecken!

6.) Beschrifte das Diagramm!

---

z. B.: 30.232; 142.162; 79.833; 135.820; 52.965

rund: 30.000; 142.000; 79.000; 135.000; 52.000

Länge im Diagramm: 3 mm; 14 mm; 8 mm; 14 mm; 5 mm

BM516

Zeichne ein Diagramm mit den Werten: 300; 150 und 70

---

Man kann das Diagramm so verändern, dass nicht über jeder Strecke die zugeordnete Zahl angegeben wird.

Zu diesem Zweck ergänzt man das Diagramm durch einen zweiten Zahlenstrahl.

Die gestrichelten Hilfslinien (Bild 2) verdeutlichen die Zeichnung.

Die Zahl 300 wird der Strecke A zugeordnet. Diese Hilfslinien lässt man später weg.

BM517

Maßstab

---

Maßstab: Verhältnis einer grafischen Darstellung zur Realität

Der Stadtplan wurde in einem Maßstab von 1:25.000 gezeichnet.

Bild 1: Zeichnung eines Hauses und Grundriss des Hauses mit den einzelnen Zimmern.

---

1 cm auf der Zeichnung entspricht 100 cm in der Realität

1 cm (auf der Karte) ≙ 1m (in der Realität)

Maßstab: 1 zu 100

Maßstab: 1:100

---

Maßstab = Kartenstrecke durch Naturstrecke

Maßstab = Kartenstrecke zu Naturstrecke

Maßstab = Kartenstrecke : Naturstrecke

Massstab={\frac {Kartenstrecke}{Naturstrecke}}

Maßstab	Kartenstrecke	Naturstrecke	Typische Anwendung
1:1.000	1 cm	10 m	Gebäude- oder Katasterplan
1:5.000	1 cm	50 m	Grundkarte
1:25.000	1 cm	250 m	Wanderkarte
1:50.000	1 cm	500 m	Radwanderkarte
1:100.000	1 cm	1 km	Autokarte
1:200.000	1 cm	2 km
1:250.000	1 cm	2,5 km
1:500.000	1 cm	5 km	Generalstabskarte
1:1.000.000	1 cm	10 km	Internationale Weltkarte
1:80.000.000	1 cm	800 km	Weltkarte (ganze Welt)

Gängiger Maßstab in den USA ist der Maßstab 1:63.000

BM518

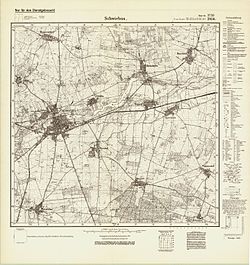
Bild 1: Messtischblatt im Maßstab 1 : 25.000

1 cm auf der Karte entspricht 25.000 cm in der Realität

1 cm ≙ 25.000 cm

1 cm ≙ 250 m

4 cm ≙ 1 km

4 Zentimeter auf der Karte entsprechen einem Kilometer im Gelände

oben rechts steht auf der Karte: „4-cm-Karte“

unten rechts steht auf der Karte 1 : 25.000

Unter einem Messtischblatt wird in Deutschland eine topografische Karte im Maßstab 1:25.000 verstanden. Hierbei entsprechen 4 cm auf der Karte 1 km in der Natur („Vierzentimeterkarte“), was diesen Kartentyp – auch wegen der damit verbundenen Präzision – besonders bei Wanderern beliebt macht.

---

Bild 2: Weltkarte im Maßstab 1 zu 35 Mill. (1 : 35.000.000)

1 m auf der Karte entsprechen 35 Mill. m in der Realität

1 m ≙ 35.000 km

1 cm ≙ 350 km

BM519

großer Maßstab

kleiner Maßstab

---

Je nach dem Inhaltsreichtum und dem Detaillierungsgrad der Karten werden große Maßstäbe, mittlere Maßstäbe und kleine Maßstäbe unterschieden. Die Adjektive „groß“ und „klein“ beziehen sich auf die Größe eines Objektes auf der Karte und nicht auf die Maßstabszahl.

Was als großer oder kleiner Maßstab bezeichnet wird, ist relativ und hängt weitgehend vom Fachgebiet oder Staat ab. Beispielsweise gilt für die Ingenieurgeologie eine Karte 1:200.000 schon als kleinmaßstäbig, für einen Geographen hingegen erst eine Übersichtskarte ab etwa 1:2.000.000. In einem großen Staat wie Russland kann 1:200.000 noch als großer Maßstab gelten, während in einem kleinen Staat wie der Schweiz dies bereits als kleiner Maßstab gewertet wird.

BM520

metrischer Maßstab

nicht-metrischer Maßstab

---

In der Kartografie werden meist runde Maßstäbe genutzt, da es sich damit besser rechnen lässt. Manchmal werden Karten zum Beispiel aus Platzgründen auf dem Kartenblatt oder bei nichtmetrischen Maßsystemen in unrunden Maßstäben publiziert (Beispiele: Stadtplan von Zürich 1:12.600; topografische Karte von Großbritannien 1:63.360 entsprechend 6 Zoll zu 1 Meile).

---

1 Zoll = 25.4 mm = 1 inch (englisch; in)

1 Meile (Landmeile) = 63.360 Zoll = 1 mile (statute mile; sm)

---

Für diese Karten bräuchte man ein Lineal mit Zolleinteilung (Bild 1), um den Abstand zwischen zwei Punkten einfach messen zu können. Ansonsten muss man etwas mehr rechnen.

---

Bild 2: am unteren Bildrand: Maßstab: ein Zoll zu einer Meile = 1 : 63360

BM521 - BM530

BM521

Maßstab 1 : 100.000

---

Weil: 1 km = 1.000 m = 100.000 cm ist, sagt man: 1 cm aufder Karte entspricht 100.000 cm in der Natur.

Man schreibt: 1 cm ≙ 100.000 cm.

1 cm ≙ 1.000 m

1 cm ≙ 1 km

Ein Maßstab gilt für eine Karte oder auch für ein Diagramm.

---

Wie lang sind folgende Strecken in Wirklichkeit, wenn sie auf einer Karte im Maßstab 1 : 100.000 folgende Längen haben?

1 cm

5 cm

8 cm

10 cm

1 mm

4 mm

8 mm

5 mm

BM522

Zeichnen den Grundriss eines Zimmers im Maßstab 1 : 100 auf kariertem Papier (Kantenlänge eines Kästchens 5 mm).

Das Zimmer ist 4,30 x 6,50 m groß.

Wie viel Kästchen zeichnest du in die Breite und wie viel in die Länge?

BM523

Koordinatensystem

---

Koordinatensysteme sind Hilfsmittel der Mathematik zur Positionsangabe.

Bild 1: Koordinaten auf einem Schachbrett. Beispiel: das weiße Feld unten rechts hat die Koordinaten „h1“

---

Eine Koordinate ist eine von mehreren Zahlen, mit denen man die Lage eines Punktes in einer Ebene oder in einem Raum angibt. Jede der zur Beschreibung erforderlichen Dimensionen wird durch eine Koordinate ausgedrückt. Wird ein Ort durch zwei Koordinaten beschrieben, beispielsweise auf der Landkarte, spricht man von einem „Koordinatenpaar“.

---

Das am häufigsten verwendete Koordinatensystem – dies gilt besonders für die Schulmathematik – ist das kartesische Koordinatensystem, das nach René Descartes (1596-1650) benannt ist.

BM524

Kartesisches Koordinatensystem

---

Ein kartesisches Koordinatensystem ist ein orthogonales Koordinatensystem. Es ist nach dem latinisierten Namen Cartesius des französischen Mathematikers René Descartes benannt, der das Konzept der „kartesischen Koordinaten“ bekannt gemacht hat. Im zwei- und dreidimensionalen Raum handelt es sich um das am häufigsten verwendete Koordinatensystem, da sich viele geometrische Sachverhalte in diesem anschaulich und übersichtlich beschreiben lassen.

---

Die beiden Richtungsachsen stehen rechtwinklig (= orthogonal) aufeinander, schneiden sich also im 90°-Winkel.

Die horizontale Achse heißt x-Achse (= Abszissenachse).

Die vertikale Achse ist die y-Achse (= Ordinatenachse).

Manchmal werden auch die Koordinatenachsen (x-Achse und y-Achse) abkürzend Abszisse oder Ordinate genannt.

Der Punkt O (0∣0), in dem sich die beiden Achsen treffen, wird Ursprung oder Koordinatenursprung oder origo (lat. „Ursprung“) genannt.

Für einen Punkt

P

mit den Koordinaten

x

und

y

schreibt man

P(x|y)

oder auch

P=(x,y)

.

BM525

Im Koordinatensystem kann man Punkte mit Hilfe von Zahlen angeben

---

Man zeichnet zwei senkrecht aufeinanderstehende Zahlenstrahlen und benennt sie mit x bzw. y. (Bild 1)

Außerdem zeichnet man einen Punkt und bezeichnet ihn mit P.

Von Punkt P aus zeichnet man senkrecht zu den Zahlenstrahlen Geraden.

Diese Geraden schneiden den Zahlenstrahl x in 6 und den Zahlenstrahl y in 3. (Bild 2)

Zu dem Punkt P gehören also die Zahlen 6 und 3.

Man sagt: Dem Punkt P ist das Zahlenpaar (6; 3) zugeordnet.

Dafür schreibt man: P (6; 3) oder

P (6|3) (Bild 3)

Dabei wird die Zahl zuerst geschrieben, die an dem mit „x“ bezeichneten Zahlenstrahl abgelesen wird. Dann wird die Zahl an der y-Achse abgelesen. Diese Reihenfolge muss stets eingehalten werden.

erst x, dann y

BM526

Zu jedem Zahlenpaar gehört ein ganz bestimmter Punkt im Koordinatensystem.

und umgekehrt:

Zu jedem Punkt im Koordinatensystem gehört ein Zahlenpaar.

---

Jeder Punkt hat ein anderes Zahlenpaar.

---

Ordne den Punkten A bis H die entsprechenden Zahlenpaare zu!

---

Lösung BM526
Bild 1: A(4; 2,5); B(2; 4) Bild 2: C(1; 1,5); D(5; 3,5); E(7; 4) Bild 3: F(1; 4); G(4; 3); H(7; 1)

BM526

Schildbürger

---

Die Schildbürger, wohnhaft im fiktiven Ort Schilda, sind Hauptakteure einer ganzen Reihe von kurzen Erzählungen, den Schildbürgerstreichen.

---

Bekannte Schildbürgerstreiche:

Die Schildbürger bauen ein Rathaus: Als die Schildbürger ein neues, pompöses Rathaus bauen, vergisst der Architekt die Einplanung von Fenstern, und das Rathaus ist innen stockfinster. Daraufhin versuchen die Schildbürger, mit Eimern das Sonnenlicht einzufangen und ins Innere zu tragen.

---

Die versunkene Glocke: Um die wertvolle Rathausglocke vor dem Feind zu schützen, beschließen die Schildbürger, sie im See zu versenken. Um sich zu merken, an welcher Stelle des Sees sie die Glocke nach dem Ende des Krieges wieder herausholen können, schnitzen die findigen Bürger eine Kerbe in den Bootsrand. Als sie nach dem Krieg merken, dass sie so die Glocke nicht wiederfinden, schneiden sie vor Wut die Kerbe aus dem Bootsrand heraus, wodurch sie freilich nur noch größer wird.

---

Erläutere weshalb sie die Glocke mit dieser Kerbe nicht wiederfanden?

BM526

Eine Summe von zwei geraden Zahlen ist immer eine gerade Zahl.

Beispiel: 62 + 74 = 136

Warum ist das so? Kannst du das beweisen?

Stimmt das für alle Zahlen?

Nenne eine Gegenbeispiel!

BM527

Kommutativgesetz:

a + b = b + a

Auch wenn man die Reihenfolge der Summanden vertauscht, erhält man dieselbe Summe.

---

Assoziativgesetz: Für alle natürlichen Zahlen a, b und c gilt:

a + (b + c) = (a + b) + c

Beim Addieren von drei Summanden kann man diese Summanden beliebig zusammenfassen.

BM528

Berechne die Summe von fünf aufeinanderfolgenden Zahlen! Die kleinste Zahl ist 175.998 Mill.

---

Rechne schriftlich: 15.679,35 Euro minus 3.837,29 Euro!

Rechne schriftlich: 688.883 plus 326.513

BM529

Ersetze den Buchstaben „G“ jeweils durch die richtigen Ziffern!

 GG4G4
+ 9G5G
------
 46537

 G2065
+ 8G7G
------
 5G4G7

 8G6G3
-17581
------
 G5G6G

 G93G2
-25G6G
------
 2G515

BM530

Subtrahieren von zwei Subtrahenden

---

Aufgabe: 658 - 234 - 112

---

Für die Lösung kann man mehrere Weg wählen.

Viel Wege führen nach Rom.

---

1. Weg

	4	2	4
	6	5	8
-	2	3	4

	3	1	2
	4	2	4
-	1	1	2

---

2. Weg

	3	4	6
	2	3	4
+	1	1	2

	3	1	2
	6	5	8
-	3	4	6

---

3. Weg

	3	1	2
	6	5	8
-	2	3	4
-	1	1	2

Alle drei Wege führen zum selben Ergebnis.

Der 3. Weg ist kurz und günstig. Dabei rechnet man folgende Einzelaufgaben

3. Weg

	3	1	2
	6	5	8	Einer: 2 + 4 = 6; 6 + 2 = 8
-	2	3	4	Zehner: 1 + 3 = 4; 4 + 1 = 5
-	1	1	2	Hunderter: 1 + 2 = 3; 3 + 3 = 6

Man rechnet also für jede Stelle einzeln die beiden Subtrahenden zusammen, bevor man sie von Minuenden abzieht.

Rechne die folgenden Aufgaben mit diesem 3. Weg. Er ist am effektivsten.

BM531 - BM540

BM531

738 - 316 - 285

Man rechnet folgende Einzelaufgaben:

	1	3	7
	7	3	8	Einer: 5 + 6 = 11; 11 + 7 = 18
-	3	1	6	Zehner: 1 + 8 + 1 = 10; 10 + 3 = 13
-	2	8	5	Hunderter: 1 + 2 + 3 = 6; 6 + 1 = 7
ÜT	1	1

---

Kontrolliere die Richtigkeit deiner Lösungen!

	7	3	8
	3	1	6
	2	8	5
+	1	3	7

Kontrolliere künftig stets die Richtigkeit deiner Lösungen!

BM532

Rechne!

---

a)


	8	7	9
-	3	2	4
-	4	3	1

---

b)


	9	6	8
-	4	1	5
-	3	4	2

---

c)


	4	7	5	6
-	1	5	0	3
-	2	1	4	2

---

d)


	6	3	8	5	9	9
-	2	0	3	1	7	3
-	3	1	2	3	0	5

BM533

Es wurden 24.840 t Fisch gefangen. Davon wurde der 4. Teil eingefroren, der 8. Teil zu Konserven verarbeitet und der Rest als Frischfisch verkauft.

Berechne die Anteile!

BM534

Subtrahieren von mehr als zwei Subtrahenden

---

	1	4	7	3	4
	9	5	7	8	3
-	1	2	5	1	9
-	3	1	8	2	7
-	2	4	3	5	8
-	1	2	3	4	5

Einzelaufgaben:

Einer: 5 + 8 + 7 + 9 = 29; 29 + 4 = 33

Zehner: 3 + 4 +5 +2 + 1 = 15; 15 + 3 = 18

Hunderter: 1 + 3 + 3 + 8 + 5 = 20; 20 + 7 = 27

Tausender: 2 + 2 + 4 + 1 + 2 = 11; 11 + 4 = 15

Zehntausender: 1 + 1 + 2 + 3 + 1 = 8; 8 + 1 = 9

BM535

Bevor das Ergebnis einer Aufgabe ermittelt wird, sollte ein Überschlag durchgeführt werden. Durch den Überschlag kennt man das Ergebnis schon ungefähr.

Beim Überschlag benutzt man Näherungswerte.

---

Beispiel:

5.901 - 5.047 - 568 = x

Überschlag:

5.900 - 5.000 - 600 = 300

x ≈ 300

---

300 ist ein Näherungswert für x.

Nun ermittelt man die genaue Differenz:

		2	8	5
	5	9	0	1
-	5	0	4	7
-		5	6	9

Dann vergleicht man das Ergebnis mit dem Überschlag:

300 ≈ 285

Das Ergebnis liegt dicht beim Überschlag.

Ein grober Fehler würde auffallen.

BM536

Vergleiche die Ergebnisse mit dem Überschlag!

---

a)


	8	9	9
-	1	3	3
-		2	1
-	2	0	2

---

b)


	7	8	6	0
-	3	2	4	5
-	1	0	1	2
-		2	3	0

---

c)


	3	5	7	2	4
-	1	2	6	3	2
-		5	7	0	9
-	1	6	8	4	6

---

d)


	8	4.	7	5	0.	0	0	0
-		5.	9	5	0.	0	0	0
-			5	7	5.	0	0	0
-					6.	3	5	0
-							8	5

BM537

Gegeben ist die Differenz der größten und der kleinsten fünfstelligen Zahl.

Gib den Nachfolger dieser Differenz an!

Lösung BM537
99.999 - 10.000 = 89.999 89.999 + 1 = 90.000

BM538

Multiplizieren natürlicher Zahlen

mit einstelligen Zahlen

---

7 * 6

7 * 30 = 7 * 3 * 10

7 * 400 = 7 * 4 * 100

7 * 13 = 7 * (10 + 3)

7 * 206 = 7 * (200 + 6)

---

3 * 60.000 = 3 * 60 * 1.000

3 * 60.000 = 180 * 1.000

3 * 60.000 = 180.000

---

3 * 300.000 = 3 * 3 * 100.000

3 * 300.000 = 9 * 100.000

3 * 300.000 = 900.000

BM539

Schriftliche Multiplikation

Schriftliches Verfahren

---

936
312 * 3

Man rechnet folgende Einzelaufgaben:

3 * 2 = 6

6
312 * 3

Weiter rechnet man:

3 * 1 = 3

36
312 * 3

Zum Schluss rechnet man:

3 * 3 = 9

936
312 * 3

BM540

Schriftliche Multiplikation

417 * 5

2085
417 * 5

Einzelaufgaben:

5 * 7 = 35

5 * 1 = 5; 5 + 3 = 8

5 * 4 = 20

---

Hier noch einmal die gleiche Aufgabe mit aufgeschriebenem Übertrag:

		2	0	8	5
	4	1	7	*	5
ÜT				3
(A)				5

BM541 - BM550

BM541

Multipliziere schriftlich!

5.429 * 5

Lösung BM541

27145
5.429 * 5

Vorgehensweise:

5 * 9 = 45; die 5 schreiben und die 4 merken

5 * 2 = 10; 10 + 4 = 14; die 4 schreiben und die 1 merken

5 * 4 = 20; 20 + 1 = 21; die 1 schreiben und die 2 merken

5 * 5 = 25; 25 + 2 = 27; die 7 schreiben und die 2 merken

Die 2 an den Anfang schreiben.

BM542

Multipliziere schriftlich!

28.468 * 8

Lösung BM542

227744
28.468 * 8

Vorgehensweise:

8 * 8 = 64; die 4 schreiben und die 6 merken

8 * 6 = 48; 48 + 6 = 54; die 4 schreiben und die 5 merken

8 * 4 = 32; 32 + 5 = 37; die 7 schreiben und die 3 merken

8 * 8 = 64; 64 + 3 = 67; die 7 schreiben und die 6 merken

8 * 2 = 16; 16 + 6 = 22; die 2 schreiben und die 2 merken

Die gemerkte 2 an den Anfang schreiben

BM543

Für ein Steakhaus werden jede Woche 125 kg Rindfleisch gekauft. Mit einer Lieferung erhält das Restaurant die Menge für 5 Wochen.

Wie viel Kilogramm Rindfleisch werden geliefert?

125 kg * 5
     625 kg

Man multipliziert eine Größe (Produkt aus Maßzahl und Einheit) mit einer natürlichen Zahl, indem man dem Produkt aus Maßzahl und natürlicher Zahl die entsprechende Einheit zuordnet:

a kg * b ) (a * b) kg

---

6,90 EURO * 5

Für die schriftliche Multiplikation kann man den Geldbetrag in Cent umrechnen. Dann führt man die schriftliche Multiplikation durch und zum Schluss rechnet man den Cent-Betrag wieder in Euro um.

6,90 EURO ➸ 690 Cent

690 Cent * 5 
   3450 Cent

3450 Cent ➸ 34,50 EURO

Man hätte auch ohne die Umrechnung in Cent multiplizeiren können:

6,90 EURO * 5

Man rechnet wie mit Cent und überlegt beim ERgebnis, dss man eine Angabe in EURO hatte. Man setzt also das Komma an die entsprechende Stelle und gibt als Benennung EURO an.

6,90 EURO * 5
   34,50 EURO

BM544

Multipliziere schriftlich

---

1.242 * 8

2.413 * 6

3.112 * 9

---

212 * 7

313 * 6

241 * 8

---

115 * 4

208 * 8

411 * 7

---

145 * 7

263 * 6

419 * 8

BM545

Multipliziere schriftlich

---

224 EURO * 2

321 kg * 8

3.122 m * 3

4.211 g * 6

---

12,80 EURO * 7

32,23 EURO * 8

64,71 EURO * 3

92,23 EURO * 4

87,50 EURO * 3

76,64 EURO * 9

BM546

Eine Rotbuche kann 900 Jahre als werden. Wie alt können 7 Rotbuchen werden?

BM547

Multipliziere alle Größen mit 7! Gib die Ergebnisse in der nächstgrößeren Einhiet an!

---

375 kg

554 kg

207 kg

892 g

257 g

803 g

849 mg

492 mg

658 mg

396 kg

BM548

Kommutativgesetz

Für alle natürlichen Zahlen a, b gilt:

a * b = b * a

Auch wenn man die Reichenfolgeder Faktoren vertauscht, erhält man dasselbe Produkt.

---

Assoziativgesetz

Für alle natürlichen Zahlen a, b, c gilt:

(a * b) * c = a * (b * c)

Beim Multiplizeiren von drei Faktoren kann man die Faktoren beliebig zusammenfassen.

BM549

Zeige, dass die folgenden Gleichungen wahr sind, ohne dass du multiplizierst!

Beispiel:

15 * 7 = 5 * 21

ist wahr, denn:

5 * 3 * 7 = 5 * 3 * 7

---

125 * 7 = 5 * 175

96 * 6 = 3 * 192

400 * 7 = 5 * 560

270 * 6 = 9 * 180

480 * 4 = 8 * 240

150 * 9 = 3 * 450

Lösung BM549
125 * 7 = 5 * 175 (man rechnet: 125:5=25; 175:7=25; also kreuzweise dividieren) 5 * 25 * 7 = 5 * 7 * 25 --- 96 * 6 = 3 * 192 (man rechnet: 96:3=32; 192:6=32; also kreuzweise dividieren) 3 * 32 * 6 = 3 * 6 * 32 ODER: 96 * 3 * 2 = 3 * 2 * 96 --- 400 * 7 = 5 * 560 (man rechnet: 400:5=80; 560:7=80; also kreuzweise dividieren) 5 * 80 * 7 = 5 * 7 * 80 --- 270 * 6 = 9 * 180 9 * 30 * 6 = 9 * 6 * 30 --- 480 * 4 = 8 * 240 8 * 60 * 4 = 8 * 4 * 60 --- 150 * 9 = 3 * 450 3 * 50 * 9 = 3 * 9 * 50