Curso de alemán para principiantes con audio/Lección 093b
Apariencia
- índice
- Lección 092b ← Lección 093b → Lección 094b
- Lección 093
- Mathematik auf Deutsch - 43
BM2101 - BM2110
[editar]BM2101
- Quadrieren
- ---
- Das Produkt einer Zahl mit sich selbst heißt Quadrat von .
- Für das Produkt „“ schreiben wir „“ und sagen, dass die Zahl quadriert wird.
- Die Quadrate natürlicher Zahlen heißen Quadratzahlen.
- ---
- Die natürlichen Zahlen 1; 4; 9; 16; 25 usw. sind Quadratzahlen.
- ---
- Nenne die ersten 10 Quadratzahlen!
Lösung BM2101 - 1; 4; 9; 16; 25; 36; 49; 65; 73; 100

- Der Begriff Quadratzahl erklärt sich daraus, dass der Inhalt einer Quadratfläche mit der Seitenlänge durch angegeben wird.
- ---
- Jedem Paar natürlicher Zahlen a und b ist durch Multiplikation eine natürliche Zahl c als Produkt zugeordnet.
- Das Quadrat jeder beliebigen natürlichen Zahl ist daher eine natürliche Zahl.
- Also gilt:
- SATZ: Zu jeder natürlichen Zahl gibt es genau eine natürliche Zahl mit .
- ---
- Das Quadrat einer ganzen Zahl ist eine ganze Zahl, denn jedem Paar ganzer Zahlen ist durch die Multiplikation eine ganze Zahl als Produkt zugeordnet.
- Da aber das Produkt zweier negativer Zahlen stets positiv ist, erhalten wir beim Quadrieren ganzer Zahlen immer nichtnegative ganze Zahlen. Wir finden laso:
- SATZ: Zu jeder ganzen Zahl gibt es genau eine ganze Zahl mit .
- ---
- Beispiel:
- Das Quadrat der Zahl ist die Zahl .
- Das Quadrat der Zahl ist ebenfalls die Zahl .
BM2102
- Jede rationale Zahl lässt sich in der Form darstellen, wobei und teilerfremde ganze Zahlen sind.
- Das Quadrat der rationalen Zahl ergibt sich zu
- .
- Sowohl der Zähler als auch der Nenner der Zahl ist nichtnegativ.
- Folglich ist auch die Zahl eine nichtnegative Zahl.
- Demnach gilt:
- SATZ: Zu jeder rationalen Zahl gibt es genau eine rationale Zahl mit .
BM2103
- Quadriere die folgenden Zahlen!
- ---
- a)
- b)
- c)
- d)
- e)
- ---
- f)
- g)
- h)
- i)
- j)
- ---
- k)
- l)
- m)
- n)
- o)
- ---
- p)
- q)
- r)
- s)
- t)
Lösung BM2103 - a)
- b)
- c)
- d)
- e)
- ---
- f)
- g)
- h)
- i)
- j)
- ---
- k)
- l)
- m)
- n)
- o)
- ---
- p)
- q)
- r)
- s)
- t)
BM2104
- Quadrat
- ---
- In der Mathematik versteht man unter dem Quadrat einer Zahl einen Term (Rechenausdruck), der die Multiplikation dieser Zahl mit sich selbst ausdrückt. Die Berechnung eines solchen Quadrates nennt man entsprechend Quadrieren. Als Symbol für das Quadrat einer Zahl wird eine hochgestellte Zwei verwendet.
- ---
- Beispiel: „5 (zum) Quadrat“ bzw. „5 hoch 2“
- Die Bezeichnung „Quadrat“ stammt aus der Geometrie: Ein Quadrat im geometrischen Sinn ist ein Viereck mit vier gleich langen Seiten und vier rechten Winkeln. Der Flächeninhalt eines solchen Quadrates wird berechnet durch Multiplikation der Seitenlänge mit sich selbst.
- Das Quadrat einer Zahl ist ein Spezialfall einer Potenz, nämlich eine Potenz mit dem Exponenten 2.
- Die Quadrate der natürlichen Zahlen nennt man Quadratzahlen:
- Es können aber auch Quadrate von rationalen Zahlen gebildet werden.
- Die Funktion , die jeder reellen Zahl ihr Quadrat zuordnet, heißt Quadratfunktion.
- ---
- Das Quadrat einer negativen Zahl ergibt immer das Quadrat ihrer (positiven) Gegenzahl: .
- ---
- Tastatur:
- Auf der deutschen PC-Tastatur liegt das „²-Zeichen“ als dritte Belegung auf der 2-Taste und kann mit Hilfe der Alt-Gr-Taste eingegeben werden. Oft kann man auch statt Alt Gr die beiden Tasten Strg und Alt verwenden. Bei einer Apple-Tastatur hingegen gibt es keine definierte Tastenkombination für das „²-Zeichen“.
BM2105
- Quadratzahl
- ---

16 Kugeln bilden ein Quadrat. - Eine Quadratzahl ist eine Zahl, die durch die Multiplikation einer ganzen Zahl mit sich selbst entsteht. Beispielsweise ist eine Quadratzahl. Die ersten Quadratzahlen sind
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, ...
- Bei einigen Autoren ist die Null keine Quadratzahl, sodass die Zahlenfolge erst mit der Eins beginnt.
- Die Bezeichnung Quadratzahl leitet sich von der geometrischen Figur des Quadrats her. Die Anzahl der Steine, die man zum Legen eines Quadrats benötigt, ist immer eine Quadratzahl. So lässt sich beispielsweise ein Quadrat mit der Seitenlänge 4 mit Hilfe von 16 Steinen legen.
- Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Quadratzahlen zu den figurierten Zahlen, zu denen auch die Dreieckszahlen und Kubikzahlen gehören. Diese Begriffe waren schon den griechischen Mathematikern der Antike bekannt.
- ---
- Eigenschaften:
- Gerade Quadratzahlen sind das Quadrat gerader Zahlen, während ungerade Quadratzahlen das Quadrat ungerader Zahlen sind.
- ---
- Formeln zum Generieren von Quadratzahlen:
- Jede Quadratzahl ist die Summe der ersten ungeraden natürlichen Zahlen.
- Diese Gesetzmäßigkeit, in englischsprachiger Literatur auch als Odd Number Theorem bekannt, wird durch die folgenden Bilder veranschaulicht.
- Von links nach rechts sind hier die ersten vier Quadratzahlen durch die entsprechende Anzahl an Kugeln dargestellt. Die blauen Kugeln zeigen jeweils den Unterschied zur vorhergehenden Quadratzahl an. Da von links nach rechts immer eine Reihe und eine Zeile hinzukommt, erhöht sich die Anzahl der blauen Kugeln jeweils um 2. Beginnend mit der 1 ganz links durchlaufen die blauen Kugeln so alle ungeraden Zahlen.
- ---
- Jede Quadratzahl ist auch die zweifache Summe der ersten natürlichen Zahlen plus der Zahl .
BM2106
- Dreieckszahl
- ---

Ein Dreieck aus zehn Steinen - Eine Dreieckszahl ist eine Zahl, die der Summe aller Zahlen von 1 bis zu einer Obergrenze entspricht. Beispielsweise ist die 10 eine Dreieckszahl, da ist. Die ersten Dreieckszahlen sind
- 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
- Bei einigen Autoren ist die Null keine Dreieckszahl, sodass die Zahlenfolge erst mit der Eins beginnt.
- Die Bezeichnung Dreieckszahl leitet sich von der geometrischen Figur des Dreiecks her. Die Anzahl der Steine, die man zum Legen eines gleichseitigen Dreiecks benötigt, entspricht immer einer Dreieckszahl. Aus zehn Steinen lässt sich beispielsweise ein Dreieck legen, bei dem jede Seite von vier Steinen gebildet wird.
- Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Dreieckszahlen zu den figurierten Zahlen, zu denen auch die Quadratzahlen und Kubikzahlen gehören. Schon Pythagoras hat sich mit Dreieckszahlen beschäftigt.
- ---
- Berechnung:
- Die -te Dreieckszahl ist die Summe der Zahlen von 1 bis .
BM2107

Zauberwürfel (Rubik’s Cube, Rubiks Würfel); - Kubikzahl
- ---
- Eine Kubikzahl (von lat. cubus, „Würfel“) ist eine Zahl, die entsteht, wenn man eine natürliche Zahl zweimal mit sich selbst multipliziert. Beispielsweise ist eine Kubikzahl. Die ersten Kubikzahlen sind
- 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, ...
- Bei einigen Autoren ist die Null keine Kubikzahl, sodass die Zahlenfolge erst mit der Eins beginnt.
- Die Bezeichnung Kubikzahl leitet sich von der geometrischen Figur des Würfels her. Die Anzahl der Steine, die man zum Bauen eines Würfels benötigt, entspricht immer einer Kubikzahl. So lässt sich beispielsweise ein Würfel mit der Seitenlänge 3 mit Hilfe von 27 Steinen legen.
- Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Kubikzahlen zu den figurierten Zahlen, zu denen auch die Quadratzahlen und Tetraederzahlen gehören.
- ---
- Die Summe zweier beliebiger Kubikzahlen kann selbst nie eine Kubikzahl sein. Anders formuliert heißt dies, dass die Gleichung
keine Lösung mit natürlichen Zahlen besitzt.
BM2108

Ein tetraedrischer Cluster der Basislänge 5, der 35 Kugeln umfasst. Jede Etage repräsentiert eine der fünf ersten Dreieckszahlen. 
Tetraeder - Tetraederzahl
- ---
- Der Name Tetraederzahl leitet sich aus einer geometrischen Eigenschaft ab. Legt man Steine zu einem Tetraeder, indem man Dreiecke übereinanderlegt, deren Seitenlängen von oben nach unten jeweils um eins zunehmen, dann entspricht die Anzahl der Steine einer Tetraederzahl.
- Dabei ist die Anzahl dieser Dreiecke und damit auch die Anzahl der Steine, die eine Kante des Tetraeders bilden. Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Tetraederzahlen zu den figurierten Zahlen, zu denen auch die Dreieckszahlen und Quadratzahlen gehören. Neben Dreiecken lassen sich auch andere Polygone als Grundrisse von Pyramiden verwenden. Diese Körper führen zu weiteren Pyramidenzahl]en.
- Ihre geometrische Repräsentation ist ein tetraedrischer Cluster in der dichtesten Kugelpackung, wie sie etwa als dekorative Aufschichtung von Orangen (oder anderen kugeligen Früchte) beim Obsthändler zu sehen sind.
- Die ersten Tetraederzahlen sind
- 0, 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, ...
- Bei einigen Autoren ist die Null keine Tetraederzahl, sodass die Zahlenfolge erst mit der Eins beginnt.
BM2109
- Quadratwurzel
- Wurzelziehen
- ---
- Beim Quadrieren ist das Produkt einer Zahl mit sich selbst zu ermitteln. Umgekehrt kann die Aufgabe gestellt werden, eine Zahl in ein Produkt aus zwei gleichen Faktoren zu zerlegen.
- ---
- Beispiel:
- Eine Quadratfläche hat den Inhalt .
- Wie groß ist die Seitenlänge dieser Fläche?
- Wir finden sie, indem wir die Zahl in das Produkt zerlegen.
- Die Seitenlänge beträgt also .
- Die Zahl heißt die Quadratwurzel von 16.
- ---
- Die Rechenoperation, bei der eine zahl in ein Produkt aus zwei gleichen Faktoren zu zerlegen ist, heißt kurz Wurzelziehen.
- Diese Operation kehrt die Operation des Quadrierens um.
- ---
- Genau genommen gibt es keine einfache Rechenoperation, um durch schriftliches Rechnen die Wurzel aus einer Zahl zu ziehen.
- Das, was es wir vom schriftlichen Addieren, Subtrahieren, Multiplizieren oder Dividieren her kennen, das gibt es für das Wurzelziehen nicht.
- ---
- Das Wurzelziehen ähnelt eher einem Rumprobieren. Man korrigiert dann nach oben und nach unten, bis man dem Ergebnis immer näher kommt. Besonders, wenn das Ergebnis sehr viele Nachkommastellen hat, wird man sicherlich irgendwann abbrechen, wenn man die gewünschte Genauigkeit erreicht hat.
- ---
- Beispiel:
- Wir suchen Quadratwurzel von 4
- (lies: „Quadratwurzel aus 4“ oder kurz „Wurzel aus 4“).
- Wir ziehen die Wurzel aus 4.
- Das ist einfach, wenn wir das kleine Einmaleins können.
- Dummerweise gibt es im kleinen Einmaleins nur 10 Quadratzahlen. Nur aus Quadratzahlen kann man die Wurzel ziehen, so dass das Ergebnis keine Nachkommastelle hat.
- ---
- ist schon schwieriger auszurechnen.
- Wir testen nacheinander:
- , ist noch zu klein.
- , ist noch zu klein, aber schon besser.
- müssen wir zur Probe mühsam mit der Hand ausrechnen oder (etwas einfacher) mit dem Taschenrechner ausrechnen.
- , ist schon zu groß. Also wieder eine etwas kleinere Zahl probieren.
- , ist etwas zu groß.
- , ist zu klein.
- , ist etwas zu klein. Also brauchen wir Nachkommastellen.
- , ist etwas zu groß. So können wir Stunden mit dem Wurzelziehen verbringen.
- , ist etwas zu groß.
- , ist etwas zu groß.
- Aber hier wollen wir dann abbrechen und mit der erreichten Genauigkeit zufrieden geben.
- oder besser
- ---
- Zum Glück gibt es heute Taschenrechner mit denen man ganz einfach eine Wurzel ziehen kann.
- Ja nach Typ des Taschenrechners gibt man erst das Wurzelzeichen ein und dann die Zahl - oder umgekehrt.
BM2110
- Quadratwurzel
- Kubikwurzel
- ---
- Quadrat- und Kubikwurzel:
- Üblicherweise wird die zweite Wurzel als Quadratwurzel oder einfach nur als die Wurzel bezeichnet und der :Wurzelexponent weggelassen:
- Die Wurzel mit dem Wurzelexponenten 3 (dritte Wurzel) bezeichnet man auch als Kubikwurzel.
- Beispiel:
- (Sprich: Die dritte Wurzel aus 8 ist 2 oder Die Kubikwurzel aus 8 ist 2)
- , deshalb ist
- , weil ist.
BM2111 - BM2120
[editar]- BM2111

Bild 1 
Bild 2 - Wurzelzeichen
- ---
- Das Wurzelzeichen (√) ist das in der mathematischen Notation verwendete Symbol für die Quadratwurzel einer Zahl bzw. für das Radizieren. Durch Angabe eines Wurzelexponenten werden mit Hilfe des Wurzelzeichens auch Wurzeln mit beliebigen Exponenten, beispielsweise Kubikwurzeln, notiert.
- ---
- Geschichte:
- Das Wurzelzeichen √ stammt wohl von dem kleinen Buchstaben und steht für radizieren (= die Wurzel zeihen; Radix = Wurzel). Eine alternative Herkunft ist ein Punkt mit einem dekorativen Aufstrich, vergleichbar einer Viertelnote. Er wurde erstmals 1525 vom deutschen Mathematiker Christoph Rudolff verwendet. Die Verlängerung des über den vollständigen Term – das Vinculum – wurde 1637 im Buch Discours de la méthode von Descartes eingeführt.
- ---
-
Bild 1
-
Bild 2
- Bild 1 und 2: Die Quadratwurzel kann mit oder ohne die kleine „2“ links über dem Wurzelzeichen geschrieben werden.
- Üblicherweise wird die kleine „2“ weggelassen, um Zeit zu sparen. (Bild 2)
- ---
-
Bild 3
-
Bild 4
-
Bild 5
-
Bild 6
-
Bild 7
- Bild 3: Der linke, kurze, horizontale Strich des Wurzelzeichens liegt etwas tiefer, als der rechte, lange, horizontale Strich.
- Bild 4 und 5: Der linke Strich liegt nicht auf selber Höhe wie der rechte und schon gar nicht höher, als der linke.
- Bild 6: Gerne werden die vertikalen Striche des Wurzelzeichens schräg nach rechts geneigt, wie bei der Schreibschrift allgemein üblich ist.
- Bild 7: Am rechten Ende des Wurzelzeichens wird manchmal ein kleiner senkrechter Strich nach unten hinzugefügt, um gerade beim schnellen Schreiben das genaue Ende des Wurzelzeichens deutlich zu markieren.
- ---

Bild 8 - Bild 8: Das Wurzelzeichen wird in einem Zug von links nach rechts gezeichnet. Der Stift wird beim Zeichnen also nicht abgesetzt.
- Gewöhnlich wird erst das Wurzelzeichen geschrieben und dann erst die Zahl darunter. Das kann aber Probleme stehen, wenn dann ein größerer Term unter die Wurzel geschrieben wird. In diesem Fall wird auch manchmal nur ein kurzes Wurzelzeichen geschrieben und erst zum Schluss der horizontale Strich nach rechts auf seine endgültige Länge gebracht und des Abschlusshäkchen nach unten hinzugefügt.
- ---
-
Bild 9
-
Bild 10
-
Bild 11
-
Bild 12
- Bild 9 - 12: Unter der Wurzel kann auch nicht nur eine Zahl stehen, sondern möglicherweise auch ein ganzer Term, der vor dem Wurzelziehen ausgewertet werden muss.
- Besonders in diesen Fällen sollte am rechten Ende des Wurzelzeichens ein kleiner senkrechter Strich nach unten hinzugefügt werden, um das genaue Ende des Wurzelzeichens deutlich zu markieren und Zweideutigkeiten als Fehlerquelle für Flüchtigkeitsfehler auszuschließen.
- ---
-
Bild 13
-
Bild 14
- Bild 13 und 14: Wenn wir nicht mit Quadratwurzeln, sondern mit Kubikwurzel rechnen, dann ist es zwingend oben links an die Wurzeln eine kleine „3“ zu schreiben.
- Wenn in einer Rechnung Quadratwurzeln und Kubikwurzeln gemischt werden, dann ist es ratsam die Quadratwurzel auch immer mit einer „2“ zu schreiben.
- ---
- Wurzel = Radix
- Wurzel ziehen = radizieren
- ---
-
Bild 15
- Bild 15: wird als Wurzelexponent bezeichnet. Die Quadratwurzel hat den Wurzelexponenten und die Kubikwurzel hat den Wurzelexponenten . Der Wurzelexponent ist eine positive natürliche Zahl (2; 3; 4; ...).
- wird als Radikand bezeichnet, die Zahl aus der die Wurzel gezogen wird.
BM2112
- Umkehroperation
- ---
- Als Umkehroperation bezeichnet man in der Mathematik die Vorschrift, mit der man zu einer bestimmten zweistelligen Rechenoperation aus deren Ergebnis und einem der beiden Operanden den jeweils anderen Operanden zurückerhält.
- Bei den Grundrechenarten ist die Umkehroperation der Addition die Subtraktion und die Umkehroperation der Multiplikation die Division.
- Für manche Operationen, so auch die Multiplikation, ist dabei allerdings ihre Umkehrung nicht mit jeder Kombination von Operanden möglich (s. u.).
- ---
- Addition
- Wenn bei der Addition die Summe und der Summand bekannt sind, erhält man den anderen Summanden durch die Subtraktion . Also ist die Subtraktion eine Umkehroperation der Addition. Da die Addition kommutativ ist, erhält man bei bekannter Summe und Summanden den anderen Summanden ebenfalls durch eine Subtraktion, nämlich .
- ---
- ---
- Multiplikation
- Wenn bei der Multiplikation das Produkt und der Faktor bekannt sind, erhält man den anderen Faktor durch die Division . Also ist die Division eine Umkehroperation der Multiplikation. Da die Multiplikation ebenfalls kommutativ ist, erhält man bei bekanntem Produkt und Faktor den anderen Faktor ebenfalls durch eine Division, nämlich .
- Nicht mehr anwendbar allerdings wird dieses Verfahren, sobald einer der beiden Faktoren und damit auch deren Produkt Null wird, da eine Division durch Null grundsätzlich verboten ist.
- (FALSCH, denn die Division durch Null ist nicht definiert.)
- ---
- ---
- Potenzieren
- ---
- Erst in späteren Lektionen wird oder behandelt. Die Umkehroperation dafür ist der Logarithmus, der auch erst später behandelt wird.
- Wenn bei der Potenz das Ergebnis und der Exponent bekannt sind, erhält man die Basis durch die Wurzel . Also ist das Wurzelziehen eine Umkehroperation des Potenzierens, mit der die Frage nach der verwendeten Basis beantwortet wird.
- Sind aber das Ergebnis und die Basis bekannt, erhält man den Exponenten durch den Logarithmus . Also ist das Logarithmieren eine weitere Umkehroperation des Potenzierens, mit der die Frage nach dem verwendeten Exponenten beantwortet wird.
- In Gegensatz zur Addition und Multiplikation hat das Potenzieren zwei Umkehroperationen, weil die Operation nicht kommutativ ist.
BM2113
- (sprich: „ Quadrat“, „ hoch zwei“ oder „ zur zweiten Potenz“)
- (sprich: „ Kubik“, „ hoch drei“ oder „ zur dritten Potenz“)
- ---
- Aufgabe:
- ,
- Manche schreiben auch nur kurz (lies: „Die Lösungsmenge ist Plus/Minus Sechs.“)
- Probe:
- ---
- Da durch das Potenzieren das Minuszeichen „unter den Tisch fällt“, muss bei der Umkehroperation, dem Wurzelziehen ein mögliches Minuszeichen wieder „auf den Tisch“.
- Die Wurzel aus einer Zahl hat immer zwei Ergebnisse: ein negatives und ein positives.
- In manchen Fällen konkreten kann man das negative Ergebnis verwerfen, beispielsweise, wenn die Anzahl von Gegenständen gefragt ist, eine Strecke oder eine Zeitdauer. Es gibt keine negative Anzahl, keine negativen Strecken und keine negative Zeitdauer.
- Aber prinzipiell gibt die Operation des Wurzelziehens erst mal eine positive Zahl und ihre negative Gegenzahl.
- ---
- Das hat eine gewisse Ähnlichkeit mit der Betragsfunktion.
- Allerdings ergibt der Betrag einer Zahl (egal ob negativ oder positiv)) immer eine positive Zahl.
- ABER:
- Wir sprechen „Fallunterscheidung“, falls die Rechnung noch weiter geht.
- ---
- Aus einer negativen Zahl kann man keine Wurzel ziehen.
- , FALSCH, denn
- , FALSCH, denn
- Aus einer negativen Zahl kann man keine Wurzel ziehen! (Bitte merken!)
- Sollte ein Term mit einem (oder einer anderen Unbekannten) unter der Wurzel stehen, dann muss sichergestellt werden, dass keine Wurzel aus einer negativen Zahl gezogen wird.
- ---
- Wenn man die Wurzel aus zieht, dann gilt die Einschränkung
- (Fallunterscheidung)
1. Fall 2. Fall
- Wegen der obigen Einschränkung fällt von den möglichen Lösungen und die zweite mögliche Lösung weg. Also:
- Lösung:
- Probe:
- (stimmt)
- Aus Neugier wollen wir noch die weggefallene als Lösung ausprobieren.
- (Und schon sehen wir, dass wir eine Wurzel aus einer negativen Zahl haben. Das geht aber NICHT. Also ist keine Lösung.
BM2114
- DEFINITION:
- Quadratwurzel aus einer nichtnegativen Zahl heißt diejenige eindeutig bestimmte nichtnegative Zahl , deren Quadrat gleich ist.
- ---
- Zahlenbereichserweiterung
- Zahlenbereiche
- Natürliche Zahlen - - alles was sich mit den Fingern abzählen lässt (mit oder ohne Null ist nur eine Frage der Definition)
- Eine Division im Bereich der natürlichen Zahlen ist nicht uneingeschränkt (nicht ohne Einschränkung; nicht immer) möglich. Als Hilfskonstruktion wurde mit Rest gerechnet. Deshalb erfolgte eine Zahlenbereichserweiterung von den natürlichen zu dem rationalen Zahlen.
- ---
- Rationale Zahlen - - mit Nachkommastelle. Darstellung durch den Quotienten (Q) , wobei a und b natürlich Zahlen sind und b ungleich Null ist.
- In den rationalen Zahlen ist das Wurzelziehen nicht uneingeschränkt möglich. Zum Beispiel ist eine Zahl mit unendlich vielen Nachkommastellen, die sich nicht in der Form darstellen lässt. (Der Beweis folgt weiter unten.) Deshalb folgt eine Zahlenbereichserweiterung auf die reellen Zahlen.
- ---
- Reelle Zahlen - - Zu den reellen Zahlen gehören auch Zahlen mit unendlich vielen Nachkommastellen, wie
- Solche Zahlen mit unendlich vielen Nachkommastellen heißen irrationale Zahl (= nicht als rationale Zahl darstellbar). Sie sind eine Teilmenge der reellen Zahlen.
- Die reellen Zahlen bestehen also aus den rationalen und den irrationalen Zahlen.
- ---
- Unendlich vielen Nachkommastellen haben auch periodische Zahlen, wie z. B. . Diese können jedoch durch einen Bruch in der Form dargestellt werden. Das sind KEINE irrationale Zahlen.
- Hier ist mir „unendlich vielen Nachkommastellen“ ist gemeint, dass sich diese Nachkommastellen NICHT periodisch wiederholen. Solche Zahlen lassen sich nicht in Form darstellen.
- ---
- Der Zahlenbereich der reellen Zahlen wird in einigen wenigen Gebieten der Mathematik, z. B. in der Elektrotechnik, noch einmal zum Zahlenbereich der komplexen Zahlen erweitert.
- ---
- Komplexe Zahlen - - (das steht für Complex) In diesem Zahlenbereich ist das Wurzelziehen aus einer negativen Zahl möglich. als imaginäre Zahl bezeichnet.
- .
- .
- Und so kann munter mit negativen Zahlen unter Wurzeln gerechnet werden. Aber nur im Zahlenbereich der komplexen Zahlen. Wer aber nicht Elektroingenieur ist kann das erst mal alles vergessen.
BM2114
- Lies vor!
- a)
- b)
- c)
- d)
- ---
- e)
- f)
- g)
Lösung BM2114 - a) : x ist eine natürliche Zahl; x ist Element der natürlichen Zahlen; x ist Element der Menge der natürlichen Zahlen
- b) : x ist eine natürliche Zahl, einschließlich Null
- c) : x ist eine natürliche Zahl, ohne Null; x ist eine positive natürliche Zahl
- d) : x ist eine ganze Zahl; x ist Element der ganzen Zahl
- ---
- e) : x ist eine rationale Zahl; x ist Element der rationalen Zahl
- f) : x ist eine reelle Zahl; x ist Element der reellen Zahl
- g) : x ist eine komplexe Zahl; x ist Element der komplexen Zahl
BM2115
- Umkehrung des Quadrierens natürlicher Zahlen
- ---
- SATZ: Es gibt natürliche Zahlen, die im Bereich der natürlichen Zahlen keine Quadratwurzel besitzen.
- ---
- Beweis: Die Zahl lässt sich im Bereich der natürlichen Zahlen nur in das Produkt aus der Zahl und zerlegen. Infolgedessen besitzt die Zahl im Bereich der natürlichen Zahlen keine Quadratwurzel. Also gibt es (wenigstens) eine natürliche Zahl, die im Bereich der natürlichen Zahlen keine Quadratwurzel besitzt.
- ---
- Um zu beweisen, dass eine Aussage falsch ist, reicht es ein (einziges) Gegenbeispiel zu zeigen.
- ---
- Beispiel:
- Aussage: Alle natürlichen Zahlen sind gerade.
- Gegenbeispiel: Die Zahl Eins. Die Zahl Eins ist eine natürliche Zahl und ungerade.
- Also ist die Aussage widerlegt.
BM2116
- Umkehrung des Quadrierens nichtnegativer rationaler Zahlen
- ---
- Das Quadrat de rationalen Zahl ist die rationale Zahl .
- Umgekehrt kann die Aufgabe gestellt werden, die Quadratwurzel aus der rationalen Zahl zu ziehen. Dann ist die Zahl in ein Produkt aus zwei gleichen nichtnegativen Faktoren zu zerlegen.
- Wegen ist die Zahl Quadratwurzel aus .
- ---
- Es soll die Quadratwurzel aus der rationalen Zahl gezogen werden.
- Wir wandeln um:
- .
- Die rationale Zahl ist Quadratwurzel aus .
- ---
- Lässt sich eine rationale Zahl auf die Form
- (lies: p und q teilerfremd)
- bringen, so ist ist die Zahl eine Quadratzwurzel aus .
- Die Mehrzahl der rationalen Zahlen lässt sich jedoch nicht auf die Form bringen.
BM2117
- Stelle die folgenden rationalen Zahlen durch Brüche dar! Versuche aus Ihnen die Quadratwurzel zu ziehen!
- a)
- b)
- c)
- d)
- e)
Lösung BM2117 - a)
- b)
- c) ;
- d)
- e)
- ---
- Es gibt nichtnegative rationale Zahlen, die im Bereich der rationalen Zahlen keine Quadratwurzel besitzen.
- Nur in einem erweiterten Zahlenbereich, in der Menge der reellen Zahlen , hat jede nichtnegative rationale Zahl genau eine Quadratwurzel.
BM2118
- Aus welchen der folgenden Zahlen kann im Bereich der rationalen Zahlen die Quadratwurzel gezogen werden?
- (Kürze vorher so weit, dass Zähler und Nenner teilerfremd sind!)
- a)
- b)
- c)
- d)
- e)
- ---
- f)
- g)
- h)
- i)
- j)
Lösung BM2118 - a)
- b)
- c)
- d) ;
- e) ;
- ---
- f) ;
- g) ;
- h) ;
- i)
- j) ;
BM2119
- Aus welchen der folgenden Zahlen kann im Bereich der rationalen Zahlen die Quadratwurzel gezogen werden?
- (Kürze vorher so weit, dass Zähler und Nenner teilerfremd sind!)
- a)
- b)
- c)
- d)
- e)
- ---
- f)
- g)
- h)
- i)
- j)
Lösung BM2119 - a)
- b) ;
- c) ;
- d) ;
- e) ;
- ---
- f)
- g)
- h)
- i)
- j) ;
BM2120
- Kann eine Primzahl eine Quadratzahl sein?
Lösung BM2120 - Nein, denn eine Primzahl hat keinen Teiler (außer Eins und sich selber).
- Quadratzahl hat einen Teiler (, der in der zweiten Potenz, also mit sich selber multipliziert, diese Quadratzahl ergibt.)
- ---
- Ja, wenn man die Eins mit zu den Primzahlen zählt.
- ABER DIE EINS WIRD NICHT ZU DEN PRIMZAHLEN GEZÄHLT.
BM2121 - BM2130
[editar]- BM2121

Illustration einer zweistelligen Verknüpfung , die aus den zwei Argumenten und das Ergebnis zurückgibt. 
Bei assoziativen Verknüpfungen ist das Endergebnis dasselbe, auch wenn die Operationen in unterschiedlicher Reihenfolge ausgeführt werden. - Zweistellige Verknüpfung
- ---
- Die Addition ist eine zweistellige Verknüpfung.
- Der Operator Plus-Zeichen benötigt zwei Zahlen, damit er Sinn macht.
- Genauso ist es mit der Subtraktion, der Multiplikation und der Division.
- ---
- Eine Verknüpfung wird ganz allgemein mit diesem Symbol dargestellt: „“
- Für das Verknüpfungszeichen „“ kann man also beispielsweise „“; „“; „“ oder „“ einsetzten.
- ---
- Eine kommutative Verknüpfung wird dann folgendermaßen dargestellt:
- (Die Addition und die Multiplikation sind kommutativ.)
- (Assoziativgesetz. Eine [zweistellige] Verknüpfung ist assoziativ, wenn die Reihenfolge der Ausführung keine Rolle spielt. Anders gesagt: Die Klammerung mehrerer assoziativer Verknüpfungen ist beliebig. Deshalb kann man es anschaulich auch „Klammergesetz“ nennen. Das Assoziativgesetz gilt auch für mehr als zwei oder drei Operanden.)
- ---
- Das Wurzelziehen ist eine einstellige Verknüpfung.
- Der Operator Wurzelzeichen benötigt nur eine Zahl.
- Auch das Quadrieren (oder ganz allgemein: das Potenzieren) ist eine einstellige Verknüpfung, benötigt also nur eine Zahl.
- BM2122
- Infixnotation
- ---
- Wir sind es gewohnt das Pluszeichen bei der Addition zwischen die beiden Summanden zu schreiben.
- Ebenso halten wir es in der Schulmathematik mit den übrigen Grundrechenarten.
- ---
- Das ist aber nicht die einzige denkbare Möglichkeit.
- Dass das Operationszeichen zwischen den beiden Operanden stehen muss ist nicht gottgegeben.
- ---
- Denkbar sind noch zwei andere Varianten: das Pluszeichen davor schreiben oder hinter beide Zahlen schreiben.
- + 21 43 (Das nennt man Präfixnotation oder Polnische Notation, weil ein polischer Mathematiker sich sehr ausführlich damit befasst hat.)
- 21 + 43 (Das ist die gebräuchliche Form, die deshalb auch viele Leute für das „Normale“ und einzig Mögliche halten. Das nennt man Infixnotation.)
- 21 43 + (Das nennt man Postfixnotation oder Umgekehrte polnische Notation.)
- ---
- Die polnische Notation hat den Vorteil, dass man damit Formeln in klammerfreier Schreibweise aufschreiben darf. Das soll aber an dieser Stelle nicht weiter vertieft werden.
BM2123
- Vorteile der Umgekehrten polnischen Notation (UPN)
- ---

- Unter Anwendern wird häufig der Vorteil der UPN zur algebraischen Notation (Infixnotation) diskutiert.
- Der auffälligste Vorteil der UPN ist, dass sie im Allgemeinen mit einer geringeren Anzahl von Tastendrücken auskommt. Um zum Beispiel die Rechnung (1+2)×(3+4) vorzunehmen, muss man im algebraischen Modus zwölf Tasten betätigen:
- Taste: (; 1 ;+; 2; ); ×; (; 3; +; 4; ); =
- Bei vielen Implementierungen lässt sich die Tastenfolge noch optimieren; dies ist allerdings genaugenommen kein „algebraisches Vorgehen“:
- Taste: 1; +; 2; =; × ; (; 3; +; 4; =
- Im UPN-Modus sind nur neun Tastendrücke erforderlich:
- Taste: 1; Enter; 2; +; 3; Enter; 4 ;+ ;×
- Es sind also drei Tasten weniger zu drücken als im algebraischen Modus; bei aufwendigeren Rechnungen ist die Ersparnis entsprechend größer.
- Ein weiterer Vorteil der UPN ist es, dass die Rechnung stets schrittweise und mit sichtbaren Zwischenergebnissen ausgeführt wird; man kann die Daten also nach und nach weiterbearbeiten; allerdings zeigen auch viele algebraische Taschenrechner Zwischenergebnisse, so weit das möglich ist, zum Beispiel beim Betätigen der „)-Taste“ den Wert des aktuellen Klammerausdrucks.
- Die Verfügbarkeit von Zwischenergebnissen erleichtert es nicht nur, die Eingaben zu kontrollieren und Fehler zu identifizieren, sondern erlaubt es im Zusammenhang mit den bei UPN verfügbaren Vertauschungsoperationen innerhalb des Stapels, jedes Zwischenergebnis einfach zu speichern, ohne dass dafür gesonderte Speicherregister benötigt würden, und später weiterzuverarbeiten. Insbesondere lässt sich der häufig vorkommende Fall, dass ein Operand gleich nochmals benötigt wird – wie etwa in der Rechnung (a−b)/b – ohne erneute Eingabe oder Speicherung von b rechnen; UPN-Rechner verfügen dafür über ein Register LASTX, das den letzten Operanden automatisch speichert.
- BM2124
- Zusammenhang des Wurzelziehens mit Potenzen
- ---
- Das Radizieren mit dem Wurzelexponenten n und das Potenzieren mit dem Exponenten n heben sich gegenseitig auf. Gemäß obenstehender Definition der Wurzel gilt für alle reellen Zahlen und für alle natürlichen Zahlen :
- ---
- Eindeutigkeit von Wurzeln aus positiven Zahlen:
- Obwohl die Wurzeloperation bei geradzahligen Wurzelexponenten und positiven Radikanden zwei Lösungen mit unterschiedlichen Vorzeichen besitzt, steht die Schreibweise mit dem Wurzelzeichen grundsätzlich für die positive Lösung (gemäß: DIN 1302 von 1999: Allgemeine mathematische Zeichen und Begriffe). Beispielsweise hat die Gleichung die beiden Lösungen und . Der Term hat jedoch den Wert +2 und nicht den Wert −2. Allgemein gilt daher für geradzahlige Wurzelexponenten
- ---
- Bei der Kubikwurzel (dritte Wurzel) gibt es nicht das Problem, dass unter der Wurzel keine negative Zahl stehen darf.
- , denn
BM2125
- Die Wurzelgesetze
- ---
- Die Wurzelgesetze werden hier ohne nähere Übungen nur kurz aufgeführt. Eine Vertiefung erfolgt erst in späteren Kapiteln.
- Die Wurzelgesetze sollen hier nur kurz angerissen werden, um schon einmal einen ersten Eindruck zu bekommen.
- ---
- Die Rechenregeln für Wurzeln ergeben sich aus jenen für Potenzen.
- Für positive Zahlen und und gelten die folgenden Rechengesetze:
- Produktregel:
- Quotientenregel:
- "Verschachtelungsregel" oder Iterationsregel:
- Definition für gebrochenen Exponenten:
- Definition für negativen Exponenten:
- Bei gleichem Radikand gilt:
- Bei negativen Zahlen und dürfen diese Rechengesetze nur angewendet werden, wenn und ungerade Zahlen sind. Bei komplexen Zahlen sind sie gänzlich zu vermeiden.
BM2126

Die ersten 4 Glieder einer Intervallschachtelung. 
Eine Intervallschachtellung zur Bestimmung der Eulerschen Zahl (e = 2,71828182845904523536). „e“ wird als blaue, jede Intervallgrenze als rote senkrechte Line dargestellt. Die Länge der roten Linien ist indirekt proportional zum Abstand zu „e“. - Berechnung der Wurzel
- ---
- Wurzeln können durch schriftliches Wurzelziehen bestimmt werden; dieses Verfahren ist jedoch von geringer praktischer Bedeutung.
- Praktisch wird die Wurzel heute mit den Taschenrechner ermittelt.
- Früher wurden Wurzel mit Tabellen (Wurzeltabellen) ermittelt, die in Tafelwerken standen. Tafelwerke enthalten daneben auch eine große Fülle von mathematischen Formeln.
- ---
- Um einen Näherungswert für eine Wurzel zu erhalten, kann man mehrere Verfahren anwenden. Dazu gehören unter anderem das Intervallhalbierungsverfahren.
- ---
- Das Heron-Verfahren, Heronsche Näherungsverfahren oder babylonische Wurzelziehen ist ein Rechenverfahren (Algorithmus) zur Berechnung einer Näherung (Approximation) der Quadratwurzel einer reellen Zahl .
- ---
- Das Schriftliche Wurzelziehen ist ein Verfahren zur Berechnung der Quadratwurzel einer rationalen Zahl, das ohne Rechner durchgeführt werden kann. Es ähnelt der schriftlichen Division und liefert bei jedem Rechenschritt eine Stelle des Ergebnisses.
- In der Schule wird das schriftliche Wurzelziehen heute kaum noch gelehrt, auch in früherer Zeit wurde es nur selten angewandt. Die Gründe sind zum einen die geringere praktische Bedeutung des Wurzelziehens im Gegensatz zu den Grundrechenarten, zum anderen sind Verfahren wie das Heron-Verfahren (babylonisches Wurzelziehen) einfacher auszuführen und liefern meist schneller eine ausreichende Genauigkeit.
BM2127

Rechenschieber 
Die Logarithmentafel als Teil eines Tafelwerkes - Tafelwerk
- ---
- Vor dem Auskommen der Taschenrechner wurden für das Ausrechnen von großen Quadratzahlen fertige Tabellen verwendet, sogenannte Quadrattafeln. Mit deren Hilfe konnte eine große Zahl sehr schnell näherungsweise quadriert werden.
- Später wurde der Rechenschieber dazu benutzt. Mit dem Rechenschieber ließen sich auch weiter Rechnungen durchführen: Grundrechenarten (plus, minus, mal, durch), Quadrieren, Wurzelziehen, Winkelfunktionen
- ---
- Als Tafelwerk wird eine Sammlung von Formeln und Tabellen unter anderem für die wissenschaftlichen Bereiche Mathematik, Physik, Chemie, Biologie, Informatik und Astronomie bezeichnet.
- Zusätzlich umfasst es auch Angaben zu Größen, Einheiten, Umrechnungen und Wertetafeln. Zum Teil sind auch Definitionen und ein Periodensystem der Elemente enthalten.
- Tafelwerke sind, neben einem Taschenrechner, meist die einzigen Hilfsmittel, die in Prüfungen erlaubt sind. Beispiele dürfen nicht enthalten sein. Anwendungen findet es vor allem im mathematischen und naturwissenschaftlichen Unterricht in den Sekundarstufen I und II sowie im Rahmen einer beruflichen Ausbildung und an Universitäten.
BM2128
- Definition der Wurzel in Meyers Lexikon
- ---
- Wurzel, in der Mathematik die Zahl, welche man durch Zerlegung einer gegebenen Zahl, des Radikanden, in mehrere gleich große Faktoren erhält.
- Die Anzahl dieser Faktoren heißt der Wurzelexponent, und nach ihr wird die Wurzel benannt.
- Es ist z. B. 8 die zweite Wurzel oder Quadratwurzel aus 64 , weil ist.
- 5 ist die dritte Wurzel oder Kubikwurzel aus 125 , weil ist
- 6 ist die vierte W. oder Biquadratwurzel aus 1296 , weil ist
- 2 ist die fünfte W. aus 32 , weil ist, etc.
- ---
- Das Wurzelzeichen , bei längern Zahlen oben noch durch einen Horizontalstrich verlängert, ist aus dem Anfangsbuchstaben r des lateinischen Wortes „radix = Wurzel“ entstanden; die Wurzelexponenten, mit Ausnahme der 2, werden demselben in der angegebenen Weise beigeschrieben.
BM2129
- Quadratwurzel
- ---
- Die Quadratwurzel (umgangssprachlich Wurzel; engl.: square root, kurz sqrt) einer nichtnegativen Zahl ist jene (eindeutig bestimmte) nichtnegative Zahl, deren Quadrat gleich der gegebenen Zahl ist.
- Das Symbol für die Quadratwurzel ist das Wurzelzeichen , die Quadratwurzel der Zahl wird also durch dargestellt. Dabei wird die Zahl beziehungsweise der Term unter der Wurzel als Radikand bezeichnet.
- Weniger verbreitet ist die ausführlichere Schreibweise
- Außerdem kann man die Quadratwurzel als Potenz ausdrücken: ist gleichwertig mit
- Zum Beispiel ist wegen und die Quadratwurzel von gleich .
- Da die Gleichung für zwei Lösungen hat, definiert man üblicherweise die Quadratwurzel als die nichtnegative der beiden Lösungen, d. h., es gilt immer
- Damit erreicht man, dass der Begriff der Quadratwurzel eindeutig ist.
- Die beiden Lösungen der Gleichung sind somit und
- Definition: Die Quadratwurzel einer nichtnegativen reellen Zahl ist diejenige nichtnegative reelle Zahl , deren Quadrat gleich ist.
- Bei der formalen Definition der Quadratwurzel sind zwei Probleme zu berücksichtigen:
- Wenn man sich auf nichtnegative rationale Zahlen beschränkt, dann ist die Quadratwurzel in vielen Fällen nicht definiert. Schon in der Antike fand man heraus, dass etwa die Zahl keine rationale Zahl sein kann.
- Im Allgemeinen existieren zwei verschiedene Zahlen, deren Quadrate mit einer vorgegebenen Zahl übereinstimmen. Beispielsweise wäre wegen auch die Zahl ein möglicher Kandidat für die Quadratwurzel aus .
- Das Symbol für die Quadratwurzel wurde zum ersten Mal während des 16. Jahrhunderts benutzt. Es wird vermutet, dass das Zeichen eine modifizierte Form des kleinen „r“ ist, das als Abkürzung für das lateinische Wort „radix“ (Wurzel) steht.
- Ursprünglich wurde das Symbol dem Radikanden vorangestellt; die waagerechte Verlängerung fehlte.
- Noch Carl Friedrich Gauß verwendete daher Klammern für kompliziertere Wurzelausdrücke und schrieb zum Beispiel anstelle von
- Im Englischen wird die Quadratwurzel als „square root“ bezeichnet, weshalb in vielen Programmiersprachen die Bezeichnung „sqrt“ für die Quadratwurzelfunktion verwendet wird.
BM2130
- Beispiele für Quadratwurzel
- ---
Quadratzahlen und deren Quadratwurzeln Radikand Quadratwurzel Radikand Quadratwurzel 1 1 121 11 4 2 144 12 9 3 169 13 16 4 196 14 25 5 225 15 36 6 256 16 49 7 289 17 64 8 324 18 81 9 361 19 100 10 400 20
- ---
- Eigenschaften und Rechenregeln
- ---
- Die Eigenschaften der Quadratwurzelfunktion ergeben sich aus den Eigenschaften der auf die Menge der nichtnegativen reellen Zahlen eingeschränkten Quadratfunktion:
- für .
- für .
- , d. h., die Quadratwurzelfunktion ist streng monoton wachsend.
- gilt mit dem reellen Betrag für beliebige reelle Zahlen .
- Dagegen gilt nur für nichtnegatives .
BM2131 - BM2140
[editar]BM2131
- Berechnung von Quadratwurzeln aus reellen Zahlen
- ---
Rationale (Näherungs-) Werte
einiger Quadratwurzeln
- Selbst dann, wenn die Quadratwurzel aus einer natürlichen Zahl gezogen werden soll, ist das Ergebnis häufig eine irrationale Zahl, deren Dezimalbruchentwicklung also ein nichtperiodischer, nicht abbrechender Dezimalbruch ist (nämlich genau dann, wenn das Ergebnis nicht natürlich ist). Die Berechnung einer Quadratwurzel, die keine rationale Zahl ist, besteht also darin, einen Näherungswert ausreichender Genauigkeit zu bestimmen. Dazu gibt es eine Reihe von Möglichkeiten:
- Schriftliches Wurzelziehen
- Hierbei handelt es sich um einen Algorithmus ähnlich dem gängigen Verfahren der schriftlichen Division.
- Intervallschachtelung
- Dieses Verfahren ist recht leicht zu verstehen, wenn auch in der praktischen Durchführung sehr mühsam.
- Beispiel (Näherungswert für ):
- Aus und folgt, dass zwischen 1 und 2 liegt. Daher probiert man , usw. durch. Aus und erkennt man, dass zwischen 1,4 und 1,5 liegen muss. Fortsetzung dieses Verfahrens mit immer mehr Nachkommastellen liefert schließlich einen Näherungswert mit der gewünschten Genauigkeit:
BM2132
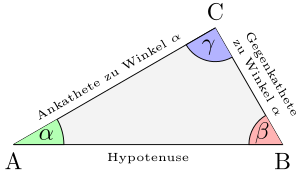
Dreieck mit dem rechten Winkel und der Ankathete und der Gegenkathete von - Rechtwinkliges Dreieck
- ---
- Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel.
- ---
- Bezeichnungen:
- Als Hypotenuse bezeichnet man die längste Seite eines rechtwinkligen Dreiecks. Sie liegt dem rechten Winkel gegenüber.
- Als Kathete wird jede der beiden kürzeren Seiten in einem rechtwinkligen Dreieck bezeichnet. Die Katheten sind also die beiden Seiten des rechtwinkligen Dreiecks, die den rechten Winkel bilden. In Bezug auf einen der beiden spitzen Winkel (in der Skizze ) des Dreiecks unterscheidet man die Ankathete dieses Winkels (die dem Winkel anliegende Kathete) und die Gegenkathete (die dem Winkel gegenüberliegende Kathete).
BM2133
- Quadratwurzeln, die keine rationalen Zahlen sind
- ---
- Als Operationszeichen für das Quadratwurzelziehen verwenden wir das Zeichen „“.
- Es wir über die Zahl gesetzt, aus der die Quadratwurzel zu ziehen ist.
- Für lesen wir: „Quadratwurzel aus .“
- Die Zahl , die unter dem Wurzelzeichen steht, heißt Radikand.
- ---
- Es soll die Quadratwurzel aus gezogen werden.
- Wir schreiben: .
- Das bedeutet: Gesucht ist eine nichtnegative Zahl , für die die Beziehung gilt.
- Unsere Vermutung ist, dass es eine solche Zahl im Bereich der rationalen Zahlen nicht gibt.
- Es gibt aber einen umfassenderen Zahlenbereich, in dem diese Zahl existiert.
- ---

Bild 1 - Das folgende Beispiel aus der Geometrie zeigt uns, wie notwendig dieser umfassendere Zahlenbereich ist.
- Uns sei der Flächeninhalt eines Quadrats bekannt, und wir suchen die Länge der Quadratseite dieses Quadrats.
- Im Bild 1 wurden vier gleichschenklige-rechtwinklige Dreiecke gezeichnet, deren Katheten die Länge 1 cm besitzen. Sie sind zu einem Quadrat angeordnet.
- ---
- Berechne die Basiswinkel und den Flächeninhalt eines jeden der vier Dreiecke in Bild 1! Welchen Flächeninhalt hat das Quadrat?
Lösung BM2133 - Dort wo sich die vier Dreieck im Zentrum des Quadrates berühren, dort ist der Winkel 90°.
- Da es gleichschenklige Dreiecke sind, sind die beiden Basiswinkel gleich groß.
- Die Basiswinkel betragen jeweils 45°.
- ---
- Jeweils zwei Dreiecke bilden zusammen ein Quadrat von einem Zentimeter Kantenlänge.
- Wir haben also zwei Quadrate mit je 1 cm2 Flächeninhalt.
- Der Flächeninhalt eines Dreiecks beträgt 0,5 cm2.
- Der Flächeninhalt des großen Quadrats, also aller vier Dreiecke zusammen, beträgt 2 cm2.
BM2134

Bild 1 - Das Quadrat hat den Flächeninhalt 2 cm2. Die Maßzahl 2 für den Flächeninhalt des Quadrats erhalten wir, wenn wir das Quadrat der Maßzahl der Seitenlänge des Quadrats bilden: .
- Also muss für die Maßzahl die Beziehung gelten.
- Die Messung einer Seite eines Quadrats mit dem Inhalt von 2 cm2 ergibt demnach einen Näherungswert für .
- Der Näherungswert ist um so genauer, je genauer die Messung erfolgen kann.
- ---

Bild 2 - Auch die Zahl , die keine rationale Zahl ist, ist einem Punkt auf der Zahlengeraden zugeordnet. Wir überzeugen uns an Hand von Bild 2 davon, dass dies tatsächlich der Fall ist.
- Der Punkt „B“ sei Nullpunkt, der Punkt „C“ Einheitspunkt der Zahlengeraden.
- Wir ordnen also dem Punkt „B“ die Zahl Null und dem Punkt „C“ die Zahl Eins zu.
- Über die Strecke konstruieren wir ein gleichschenklige-rechtwinkliges Dreieck mit der Strecke als Kathete.
- Die Länge der Strecke beträgt dann Längeneinheiten.
- Die Strecke tragen wir von 0 aus auf dem positiven Teil der Zahlengeraden ab und erhalten den Punkt „D“.
- Wegen beträgt die Länge der Strecke ebenfalls Längeneinheiten.
- Dem Punkt „D“ ist also keine rationale Zahl zugeordnet, denn sonst wäre die Zahl wegen der Eindeutigkeit der Streckenabtragung eine rationale Zahl.
- Auf der Zahlengeraden gibt es also Punkte, denen keine rationale Zahl zugeordnet werden kann.
- Um diese „Lücken“ auf der Zahlengeraden zu schließen, wird ein Zahlenbereich benötigt, der außer den rationalen Zahlen auch noch Zahlen enthält, die keine rationalen Zahlen sind.
BM2135
- Beweis der Irrationalität der Wurzel aus 2 bei Euklid
- ---
- In der Abhandlung Elemente des griechischen Mathematikers Euklid ist ein Beweis dafür überliefert, dass die Quadratwurzel von 2 irrational ist. Dieser zahlentheoretische Beweis wird durch Widerspruch (Reductio ad absurdum) geführt und gilt als einer der ersten Widerspruchsbeweise in der Geschichte der Mathematik. Aristoteles erwähnt ihn in seinem Werk Analytica priora als Beispiel für dieses Beweisprinzip. Der unten angeführte Beweis stammt aus Buch X, der Elemente. Es wird jedoch allgemein angenommen, dass die Textstelle nicht von Euklid selbst stammt.
- Irrationale Größenverhältnisse waren schon dem Pythagoreer Archytas von Tarent bekannt, der Euklids Satz nachweislich schon in allgemeinerer Form bewies. Früher glaubte man, das Weltbild der Pythagoreer sei durch die Entdeckung der Inkommensurabilität in Frage gestellt worden, da sie gemeint hätten, die gesamte Wirklichkeit müsse durch ganzzahlige Zahlenverhältnisse ausdrückbar sein. Nach heutigem Forschungsstand trifft das aber nicht zu.
- ---
- Behauptung:
- Die Quadratwurzel aus 2 ist eine irrationale Zahl.
- ---
- Beweis:
- Die Beweisführung erfolgt nach der Methode des Widerspruchsbeweises, das heißt, es wird gezeigt, dass die Annahme, die Wurzel aus 2 sei eine rationale Zahl, zu einem Widerspruch führt (lateinisch: reductio ad absurdum).
- Es wird also angenommen, dass die Quadratwurzel aus 2 rational ist und sich somit als Bruch darstellen lässt. Es wird ferner angenommen, dass und teilerfremde ganze Zahlen sind, der Bruch also in gekürzter Form vorliegt:
- Das bedeutet, dass das Quadrat des Bruchs gleich 2 ist:
- ,
- oder umgeformt:
- .
- Da eine gerade Zahl ist, ist auch gerade.
- Daraus folgt, dass auch die Zahl gerade ist.
- (Bemerkung: Eine ganze Zahl wird gerade bzw. ungerade genannt, je nachdem ob sie durch 2 teilbar bzw. nicht teilbar ist. Das heißt: Eine gerade Zahl hat die Form und eine ungerade Zahl die Form , wobei eine natürliche Zahl 1, 2, 3, … ist. Da und ist, ist das Quadrat einer ganzen Zahl genau dann gerade, wenn selbst gerade ist.)
- Die Zahl lässt sich also darstellen durch:
- , wobei eine ganze Zahl ist.
- Damit erhält man mit obiger Gleichung:
- und hieraus nach Division durch 2
- .
- Mit der gleichen Argumentation wie zuvor folgt, dass und damit auch eine gerade Zahl ist.
- Da und durch 2 teilbar sind, erhalten wir einen Widerspruch zur Teilerfremdheit.
- Dieser Widerspruch zeigt, dass die Annahme, die Wurzel aus 2 sei eine rationale Zahl, falsch ist und daher das Gegenteil gelten muss.
- Damit ist die Behauptung, dass irrational ist, bewiesen.
BM2136
- Berechnung von Näherungswerten nichtrationaler Quadratwurzeln
- ---
- Die Zahl ist eine nichtrationale Zahl.
- Wir haben gesehen, dass wir einen Näherungswert für diese zahl durch Messung einer geeigneten Strecke finden können.
- Die Genauigkeit für einen solchen Näherungswert, der durch Messung gefunden wird, ist nicht sehr groß. Wir benötigen ein Verfahren, das Näherungswerte von nichtrationalen Quadratwurzeln mit einer besseren Genauigkeit liefert.
- ---
- Wir berechnen die Zahl durch folgendes Verfahren:
- 1. Schritt: Wegen und gilt
- 2. Schritt: Wir quadrieren die Zahlen 1,1 bis 1,9
1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 1,21 1,44 1,69 1,96 2,25 2,56 2,89 3,24 3,61
- Wegen und gilt
- 3. Schritt: Wir quadrieren die Zahlen 1,41 bis 1,49
1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,9881 2,0164 2,0449
- Weitere Quadrate brauchen hier nicht errechnet werden, da schon mit überschritten wurde.
- Wegen und gilt .
- Fährt man in dieser Weise fort, kann man für die nichtrationale Zahl mit beliebiger Genauigkeit rationale Zahlen als Näherungswerte errechnen.
- Die drei Schritte liefern uns die Näherungswerte
- ; ; .
- ---
- Ist ein Näherungswert einer Quadratwurzel gegeben, so kann auf der Zahlengeraden die Lage des Punktes angegeben werden, dem dieser Näherungswert zugeordnet ist.

Intervallschachtelung: - 1. Schritt: (rot)
- 2. Schritt: (grün)
- 3. Schritt: (blau)
BM2137
- Ist umgekehrt ein Punkt auf der Zahlengeraden gegeben, dem keine rationale Zahl zugeordnet ist, so kann die Lage des Punktes auf der Zahlengeraden mit diesem Verfahren der „fortgesetzten Zehnteilung“ durch die Angabe der Stellen eines Dezimalbruchs - jedenfalls in Gedanken - beliebig genau beschrieben werden.
- ---
- Ermittle mit dem Taschenrechner die Quadratwurzel für folgende Zahlen:
- (Der Taschenrechner von google lässt sich aufrufen, indem man eine beliebige Rechenaufgabe in die Suchleiste eingibt, beispielsweise „2+2“. Man kann auch die Wurzelaufgabe direkt in die Suchleiste eingeben: „sqrt(2)“ (sqrt steht für square root).
- a) 7,62
- b) 0,246
- c) 78,45
- ---
- d) 64,8
- e) 7,01
- f) 0,33
Lösung BM2137 - a)
- b)
- c)
- ---
- d)
- e)
- f)
BM2138
- Rechne oder vereinfache die Terme!
- ---
- a)
- b)
- c)
- d) ; ;
- ---
- e) (Durch Ausklammern in ein Produkt umwandeln.)
- f) (Durch Ausklammern in ein Produkt umwandeln.)
- g) (Durch Ausklammern in ein Produkt umwandeln.)
Lösung BM2138 ??? - a)
- b)
- c)
- d) ; ;
- ---
- e) (Durch Ausklammern in ein Produkt umwandeln.)
- f) (Durch Ausklammern in ein Produkt umwandeln.)
- g) (Durch Ausklammern in ein Produkt umwandeln.)
BM2139
- Klammerregeln
- ---
- Zusammengesetzte Klammern werden vorteilhaft von innen nach außen aufgelöst.
- 1. Schritt: Alle inneren Klammern werden aufgelöst, die äußeren Klammern bleiben unverändert.
- 2. Schritt: Die äußere Klammer wird aufgelöst.
- ---
- Beispiel:
BM2140
- Potenzgesetze
- ---
- 1.)
- ---
- 2.)
- ---
- 3.)
- ---
- 4.) (Das ist so definiert! Basta! Merken!)
BM2141 - BM2150
[editar]BM2141
- Ausmultiplizieren
- ---
- 01.)
- 02.)
- ---
- 03.)
- 04.)
- ---
- 05.)
- 06.)
- ---
- 07.)
- ---
- 08.)
- ---
- 09.)
- ---
- 10.)
- ---
- 11.)
BM2142
- Ausklammern
- ---
- 01.)
- ---
- 02.)
- ---
- 03.)
- ---
- 04.)
- ---
- 05.)
- ---
- 06.)
- ---
- 07.)
- ---
- 08.)
- ---
- 09.)
- ---
- 10.)
- ---
- 11.)
BM2143
- Binomische Formeln:
- 1.)
- ---
- 2.)
- 3.)
- ---
- Die Herleitung der binomischen Formeln erfolgte in den beiden letzten Übungen.
- ---
- Die binomischen Formeln müssen auswendig gelernt werden, denn darauf wird bei der Umformung von Gleichungen oft zurückgegriffen.
BM2144
- Potenzgesetze
- ---
- Was ist richtig und was ist falsch?
- Führe Beispiele mit einfachen Zahlen an!
- Finde Zahlenbeispiele, die auch für die falschen Potenzgesetze eine wahre Aussage ergeben!
- a)
- b)
- c)
- d)
- ---
- e)
- f)
- g)
- h)
- ---
- i)
- j)
- k)
- l)
- ---
- m)
- n)
- o)
- p)
- ---
- q)
- r)
- s)
- t)
- ---
- u)
- v)
- w)
- x)
- ---
- y)
- z1)
- z1) ist nicht definiert
Lösung BM2144 - Nur a), n) und y) sind wahr:
- a)
- n)
- y)
- ---
- Beispiele:
??? richtige und falsche
BM2145
- Wurzelgesetze
- ---
- Produktregel:
- Erkläre die Zwischenschritte, wie man von der linken Seite der Gleichung zur rechten Gleichungsseite kommt!
1. Lösung BM2145
- ---
- Quotientenregel:
- Erkläre die Zwischenschritte, wie man von der linken Seite der Gleichung zur rechten Gleichungsseite kommt!
2. Lösung BM2145
- ---
- Erkläre die Zwischenschritte, wie man von der linken Seite der Gleichung zur rechten Gleichungsseite kommt!
3. Lösung BM2145 - Erweitern mit
- ---
- Wenn man eine Wurzel nicht auslösen kann, dann sollte sie bei einem Bruch zumindest immer aus dem Nenner entfernt werden.
- Dazu erweitert man den Bruch mit der Wurzel, die im Nenner steht. Das ergibt ein Quadrat der Wurzel und löst damit die Wurzel auf. Dann hat man zwar die gleiche Wurzel im Zähler, aber dort stört sie bei einem schriftlichen Rechenverfahren nicht so sehr.
- Beispiel:
- Wir rechnen mit dem Taschenrechner: .
- Eine größere Genauigkeit gibt der google-Taschenrechner nicht her.
- Wenn wir eine größere Genauigkeit wollen, dann müssen wir schriftlich rechnen.
- ; Wie oft passt eine unendlich lange Zahl in die Drei?
- Viel besser lässt sich rechnen, wenn der Dividend unendlich lang ist und der Divisor eine endlich lange Zahl ist.
- (Dividend durch Divisor = Quotient)
- lässt sich viel einfacher rechnen. Zumindest lässt sich diese Rechnung einfacher bei der schriftlichen Division aufschreiben.
BM2146
- Rechne!
- ---
- a) (Multipliziere aus und vereinfache!)
- b) (Klammer aus und vereinfache!)
- c) (Klammer aus und vereinfache!)
- d) (Löse die Klammern auf und vereinfache!)
- ---
- e) (Löse die Klammern auf und vereinfache!)
- f) (Löse die Klammern auf und vereinfache!)
- g) (Löse die Klammern auf und vereinfache!)
- h) (Werte den Term aus!)
- ---
- i) (Werte den Term aus!)
- j)
- k)
- l)
Lösung BM2146 - a) (Multipliziere aus und vereinfache!)
- ---
- b) (Klammer aus und vereinfache!)
- ---
- c) (Klammer aus und vereinfache!)
- ---
- d) (Löse die Klammern auf und vereinfache!)
- ---
- e) (Löse die Klammern auf und vereinfache!)
- ---
- f) (Löse die Klammern auf und vereinfache!)
- ---
- g) (Löse die Klammern auf und vereinfache!)
- ---
- h) (Werte den Term aus!)
- ---
- i) (Werte den Term aus!)
- ---
- j)
- ---
- k) für , denn ist nicht definiert
- ---
- l) (Jede Zahl oder Term zur 1. Potenz erhoben ist gleich der Zahl oder dem Term Ausdruck selber.)
BM2147
- Die negative Potenz ist nur eine anderen Schreibweise für den reziproken Wert der Potenz mit positivem Exponenten.
- Jede Potenz mit negativem Exponenten ist gleich dem reziporken Wert der Potenz mit positivem Exponenten:
- ---
- ---
- Schreibe die folgenden Brüche als Potenz, so dass die Bruchstriche verschwinden!
- a)
- b)
- c)
- d)
- ---
- e) Was ist der Unterschied zwischen und
Lösung BM2147 - a)
- b)
- c)
- d)
- ---
- e) : Beispiel:
- : Beispiel:
BM2148
- Wurzeln und Potenzen mit gebrochenem Exponenten sind verschiedene Darstellungsformen des gleichen Sachverhaltes.
- Wurzeln werden in folgender Weise als Potenz geschrieben:
- Der Zähler des gebrochenen Exponenten der Potenz wird die Potenz des Radikanden, und der Nenner ist der Exponent der Wurzel.
- (; und sind ganze Zahlen mit )
- ---
- Beispiel:
- ---
- Die Potenzen mit gebrochenen Exponenten werden wie folgt als Wurzel geschrieben:
- Die Basis wird als Radikand mit dem Zähler des gebrochenen Exponenten potenziert und als Wurzelexponent der Nenner des Exponenten genommen.
- (Einschränkung: ; und sind ganze Zahlen mit )
- ---
- Beispiel:
- ---
- Das Radizieren, zum Lösen der Wurzelaufgabe, ist eine Umkehroperation zum Potenzieren (zur Lösung der Potenzaufgabe).
- Beim Potenzieren sind Bais und Exponent bekannt, undder Potenzwert wird gesucht.
- Beim Radizieren sind der Potenzwert und der Exponent bekannt, und gesucht ist die Basis.
- ( ist eine natürliche Zahl mit )
- Dabei wird vorausgesetzt, dass und nichtnegative Werte sind.
- ---
- Definition:
- Ist eine nichtnegative reelle Zahl () und eine natürliche Zahl, so versteht man unter der n-ten Wurzel aus der Zahl diejenige Zahl , deren n-te Potenz ist.
- Schreibweise:
- (mit )
- Bezeichnungen:
- Radikand
- Wurzelexponent
- Wurzelwert
- ---
- Die Rechenoperation Wurzelziehen oder Radizieren hat ein eindeutig bestimmtes Ergebnis, da immer nur der positive Wurzelwert betrachtet wird:
- , denn und
- , denn zwar ist aber es gilt nicht
- ---
- Es ist nicht möglich den Wurzelwert aus negativen Radikanden zu bestimmen, jedenfalls nicht im Berech der reellen Zahlen.
- In der vorgegebenen Wurzel ist der Radikand immer negativ, wenn ein Wert für eingesetzt wird, der größer als 4 ist. Das heißt, für alle Werte , die nicht größer als 4 sind, ist der Radikand positiv und der Wurzelwert kann somit bestimmt werden.
- Bemerkung: kann insbesondere auch negative Werte annehmen.
- Beispiel:
- ---
- Potenzen mit gleichen Exponenten können dividiert werden, indem der Quotient der Basen mit dem gemeinsamen Exponenten potenziert wird.
BM2149
- a) Über welche Zwischenschritte kann man in umformen?
- ---
- Rechne!
- b)
- c)
- ---
- Mache die Nenner rational!
- d)
- e)
- f)
- g)
- h)
- i)
Lösung BM2149 - a)
- ---
- b)
- ---
- c)
- ---
- d)
- ---
- e)
- ---
- f)
- ---
- g)
- ---
- h)
- ---
- i)
- Rechenregel:
BM2150

Bild 1 - Aus zwei gleichen Quadraten mit der Kantenlänge 1,20 m wurden zwei identische Dreiecke herausgeschnitten.
- Die kleinen Dreiecke sind dem großen Dreieck ähnlich.
- Ist die blaue oder die rote Fläche größer?
- Wie große ist die blaue Fläche?
- Wie groß ist die rote Fläche?
1. Lösung BM2150 - Die rote Fläche ist größer.
- ---
- Warum?
2. Lösung BM2150 - Auf den ersten Blick mag man den Eindruck haben, dass sowohl die blaue als auch die rote Fläche ungefähr 50 % des Dreiecks einnimmt. Dem ist aber nicht so.
- ---
- Wir wollen zuerst für das blaue Dreieck das Flächenverhältnis zwischen blauer und weißer Fläche bestimmen.
- Wir haben 10 kleine, blaue Dreiecke und 6 kleine, weiße Dreiecke. Wir haben also eine Verhältnis von 10 zu 6. Oder als Forme ausgedrückt: .
- Welchen Anteil hat nun aber die blaue Fläche am gesamten großen Dreieck?
- Da es über den Daumen gepeilt 50 % sind, muss man also einen Bruch aufstellen, der als Ergebnis um die 0,5 hat.
- kann es nicht sein, denn das ist knapp 2.
- ---
- Wie muss der Bruch lauten?
3. Lösung BM2150 - Insgesamt hat das Dreieck 16 Felder, nämlich 10 blaue und 6 weiße.
- Welchen Anteil hat nun die blaue Fläche am gesamten großen Dreieck?
- ---
- Wie muss der Bruch lauten?
4. Lösung BM2150 - , also
- .
- Also sind 38,7 % der Fläche des großen Dreiecks blau.
- ---
- Und wie viel Prozent der Dreiecksfläche am anderen Dreieck ist rot?
5. Lösung BM2150 - , also
- .
- Also sind 66,7 % der Fläche des großen Dreiecks rot.
- ---
- Im Vergleich zum blauen Dreieck, dessen blaue Fläche 38,7 % einnimmt, ist die rote Fläche also deutlich größer.
- Wir machen die Brüche zum Größenvergleich gleichnamig:
- Die rote Fläche ist also um größer.
- ---
- Stimmt das? Rechne!
6. Lösung BM2150 - Nein, das stimmt nicht!
- Die rote Fläche ist nur um größer.
- ---
- Gegenprobe:
- Wir bilden die Differenz der realtiven Flächenanteile von rot und blau.
- Das sollte sein.
- Ist es aber nicht.
- ---
- Wo liegt der Fehler?
7. Lösung BM2150 - Der Fehler lag schon in der 4. Lösung.
- Dort hatten wir gerechnet:
- Der Ansatz ist aber falsch:
- Das große Dreieck hat 16 Felder (10 blaue und 6 weiße). UND das Dreieck hat 10 blaue Felder. Wir suchen als das Verhältnis der blauen Felder zur Geamtzahl:
- Also ist 62,5 % der Fläche des großen Dreiecks blau.
- Das müssen wir noch mit der Fläche des roten Dreiecks vergleichen, die wir in der 5. Lösung ausgerechnet hatten.
- , also (6 rote Felder, 3 weiße Felder)
- .
- Also sind 66,7 :% der Fläche des großen Dreiecks rot.
- ---
- Ist die blaue oder die rote Fläche größer?
- Die rote Fläche (66,7 :%) ist größer als die blaue Fläche (62,5 %).
- Die rote Fläche ist also (wie schon weiter oben in der 5. Lösung gesagt) größer, aber nicht um so viel.
- ---
- Wie große ist die blaue Fläche genau?
- Und wie groß ist die rote Fläche genau?
8. Lösung BM2150 - Das große Dreieck hat eine Fläche von
- Die blaue Fläche nimmt davon 62,5 % ein:
- .
- ---
- Die rote Fläche nimmt davon 66,7 % ein:
- .
- índice
- Lección 090b ← Lección 091b → Lección 092b
- Lección 091












































































































![{\displaystyle {\sqrt {a}}={\sqrt[{2}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/703568c12856d81ba503e45df79ef89b2eac426a)
![{\displaystyle {\sqrt[{3}]{8}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f378331b0d609846c021c1a0bbff0a4fc1755c3)














































![{\displaystyle b={\sqrt[{a}]{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7160fd4c4985c0367e50686d6e4d9d91502a3f8b)









































































































































![{\displaystyle \left({\sqrt[{n}]{a}}\right)^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64cb04ba3b309b574960aaf2b7141e4faae06216)
![{\displaystyle {\sqrt[{}]{}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2728884d0378cc133178d711fe6fef12aad386f6)



![{\displaystyle {\sqrt[{2}]{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b6caa44c96c5446c370b7e361bc7995a5f88e6b)
![{\displaystyle {\sqrt[{2n}]{x^{2n}}}=|x|\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd28bc64b4878d053459208c9b779b449d1f450f)
![{\displaystyle {\sqrt[{3}]{-8}}=-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b130ad49972cfb951cd0334b8fce072ad343026)


![{\displaystyle {\sqrt[{n}]{a}}\cdot {\sqrt[{n}]{b}}={\sqrt[{n}]{a\cdot b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb1cdc44e892d181f2e52332608a940e0d9f9a6b)
![{\displaystyle {\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}={\sqrt[{n}]{\frac {a}{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a051c5fb0f6593e2d1e6a84d3ab614ffbab3eb2)
![{\displaystyle {\sqrt[{k}]{\sqrt[{n}]{a}}}={\sqrt[{k\cdot n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9ba6c3da4cf43df9e38977b96c9daf8be46f8dc)
![{\displaystyle a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}=\left({\sqrt[{n}]{a}}\right)^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eda44fafa5645a4a928e1952671789b7666557da)

![{\displaystyle {\sqrt[{n}]{a}}\cdot {\sqrt[{m}]{a}}=a^{{\frac {1}{n}}+{\frac {1}{m}}}={\sqrt[{nm}]{a^{n+m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c1ca52010ec4da294c61cd6870a77b9085e2f72)








![{\displaystyle (5={\sqrt[{3}]{125}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2907a696cb868bb8dda9d9909a1dc2a71ddd924)

![{\displaystyle (6={\sqrt[{4}]{1296}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41871cc7a644c4225cf5b368d053a124a559f709)

![{\displaystyle (2={\sqrt[{5}]{32}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e77d708ae72040a769781cef87c9bffaad8c1b8)




![{\displaystyle {\sqrt[{2}]{y}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09a5c859d31b85b7d986e72a6c54f1fa8316031)























































































![{\displaystyle 2[20x-3(4-34)+10(2-x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9deeb11fd5f39bf119fe1d909ccf9e9b8c4987)






![{\displaystyle 2[20x-3(4-34)+10({{\tfrac {1}{6}}+{\tfrac {2}{5}}}-x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e57c32f18b3dee0e0379a61e2edc6cd2b4dfbce7)
![{\displaystyle 2[20x-3(4-34)+10({{\tfrac {5}{30}}+{\tfrac {12}{30}}}-x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c428523d1310865cdddc485899cb57cd15c316ce)
![{\displaystyle 2[20x-3(4-34)+10({\tfrac {17}{30}}-x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab3458b3eb752cdd5cb76e0435d90c014018ded)
![{\displaystyle 2[20x-3(4-34)+10({\tfrac {17}{30}}-{\tfrac {30x}{30}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/607263e0c835ffb90c2b77c461a6a71c650559cb)
![{\displaystyle 2[20x-3(4-34)+10({\tfrac {17-30x}{30}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b52360c75463b3ad46a08d8f2eeb1a7900e2494)
![{\displaystyle 2[20x-3(4-34)+{\tfrac {10(17-30x)}{30}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95bd41b4e020fe4cbcc1cab66f901184be0e36cc)
![{\displaystyle 2[20x-3(4-34)+{\tfrac {17-30x}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1a809878aad648193e7fbab12e617bd0edbb7f1)
![{\displaystyle 2[20x-3(-30)+{\tfrac {17-30x}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aad542c7bbfa6969f400bdaa3ae2a0cb8993aa6c)
![{\displaystyle 2[20x-(-90)+{\tfrac {17-30x}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80eab22e2745f82b505afcb2b4fec883250ce2f4)
![{\displaystyle 2[20x+90+{\tfrac {17-30x}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d0ce540d1838ff2de063b26054da24a6f90b48f)
![{\displaystyle 2[{\tfrac {60x}{3}}+{\tfrac {270}{3}}+{\tfrac {17-30x}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37314c1b63163ab4a14a02f4d0b046d1062d667)
![{\displaystyle 2[{\tfrac {60x+270+(17-30x)}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a10acf95f1ab4e6a3541782b5f736c11287bbe1)
![{\displaystyle 2[{\tfrac {30x+287}{3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc9d49fd1ed7ba7cd4c0f5d251d60fe15b248515)

















































































![{\displaystyle (a+x)+[3(2a-x)-5]-(a-6)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a70fc9ee003c808024bbb1dc1068ba0b36be47)
![{\displaystyle (3u-2v)-(u+w)-[u-(v+w)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf7d306190e2761b65b733d03d85d52e9b5e256e)
![{\displaystyle 3\cdot [40x-2(5x+8)+10(2-x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb4b38fd3bceaca38ab4c350c0b72af9d4aee83)
![{\displaystyle 10r-[(5m+2n)-(6m-n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec33b8776ccce89ac0870086417ff16cbafaa406)








![{\displaystyle {\begin{aligned}(a+x)+[3(2a-x)-5]-(a-6)&=a+x+[6a-3x-5]-a+6\\&=a+6a-a+x-3x-5+6\\&=6a-2x+1\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/905ed36a3b3bd1fa5d2e4c9acfd0798879c9816f)
![{\displaystyle {\begin{aligned}(3u-2v)-(u+w)-[u-(v+w)]&=3u-2v-u-w-[u-v-w]\\&=3u-2v-u-w-u+v+w\\&=3u-u-u-2v+v-w+w\\&=u-v\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/044994cddcef9f7ab9e2374a5b72dbeac9187791)
![{\displaystyle {\begin{aligned}3\cdot [40x-2(5x+8)+10(2-x)]&=3\cdot [40x-10x-16+20-10x]\\&=120x-30x-48+60-30x\\&=60x+12\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9182df8416a4f78938dd5272d7cea200809a9540)
![{\displaystyle {\begin{aligned}10r-[(5m+2n)-(6m-n)]&=10r-[5m+2n-6m+n]\\&=10r-5m-2n+6m-n\\&=10r+m-3n\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/398bed4bfb2d913d40e1b5b59518097b14d20c63)























![{\displaystyle {\sqrt[{r}]{a^{s}}}=a^{\tfrac {s}{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68f14cef0bc7c5dae2097ba826be196d593dd7a)


![{\displaystyle {\sqrt[{3}]{a^{2}}}=a^{\tfrac {2}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecc837fbe1d135fdc648533162302c2c555744f5)
![{\displaystyle a^{\tfrac {x}{y}}={\sqrt[{y}]{a^{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331b1c028167954086d54987b50f4f3009a3fd38)
![{\displaystyle a^{\tfrac {4}{7}}={\sqrt[{7}]{a^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0198c46e6f1ce3b93eedfbf223416dd6d90cb0)

![{\displaystyle a={\sqrt[{7}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9187d17de6bdbb6d3e8b0ce64d77fcd9a7b997fb)

![{\displaystyle a={\sqrt[{n}]{b}}\Longleftrightarrow a^{n}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa5b4f9279c418f5aa5d3c0ce17bfe8954b885a)





![{\displaystyle {\sqrt[{4}]{4-x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe298a5236e18fbdd50b79968f2e0fcb4c23c21)

![{\displaystyle {\sqrt[{4}]{4-(-4)}}={\sqrt[{4}]{8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/917e803a84a3570bc9767b16c8cc0a83f65f9270)

![{\displaystyle {\frac {\sqrt[{n}]{a^{m}}}{\sqrt[{q}]{a^{p}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc30d27e5c93172f163d44ac16acba639eb53e1f)
![{\displaystyle {\sqrt[{nq}]{\frac {a^{mq}}{a^{np}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f739f882e44c98644dc96349bf754096a3c6ee)

![{\displaystyle {({\sqrt[{2}]{x^{3}}})}^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71571141e0c11b6ce7d8d0515c95043d0c619647)

![{\displaystyle {\frac {2}{3{\sqrt[{3}]{5}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4108a47a9e0a6c34f872a9110aeeb58578a78b2)
![{\displaystyle {\frac {1}{\sqrt[{3}]{{(a+b)}^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884bd18104e7e54dbe2a7fa27894428114b3b788)


![{\displaystyle {\frac {2}{3{\sqrt[{3}]{4}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e2af2d7c1cb75ceb643cf9119b8a07cd1b33583)
![{\displaystyle {\begin{aligned}{\frac {\sqrt[{n}]{a^{m}}}{\sqrt[{q}]{a^{p}}}}&={\frac {a^{\frac {m}{n}}}{a^{\frac {p}{q}}}}\\&=a^{{\frac {m}{n}}-{\frac {p}{q}}}\\&=a^{\frac {mq-np}{nq}}\\&={\sqrt[{nq}]{\frac {a^{mq}}{a^{np}}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f227df1656e7f0cf062d70020b8773ea1ef21eb4)

![{\displaystyle {\begin{aligned}{({\sqrt[{2}]{x^{3}}})}^{4}&={(x^{\frac {3}{2}})}^{4}\\&=x^{6}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c90da1866049660fefbc1937cd94347c395733)

![{\displaystyle {\begin{aligned}{\frac {2}{3{\sqrt[{3}]{5}}}}&={\frac {2{\sqrt[{3}]{5}}{\sqrt[{3}]{5}}}{3{\sqrt[{3}]{5}}{\sqrt[{3}]{5}}{\sqrt[{3}]{5}}}}\\&={\frac {2{\sqrt[{3}]{25}}}{3{\sqrt[{3}]{5}}^{3}}}\\&={\frac {2{\sqrt[{3}]{5}}{\sqrt[{3}]{5}}}{3\cdot 5}}\\&={\frac {2{\sqrt[{3}]{5}}{\sqrt[{3}]{5}}}{15}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf204478565baf62c3908072ba9c2b3bc07c82d)
![{\displaystyle {\begin{aligned}{\frac {1}{\sqrt[{3}]{(a+b)^{2}}}}&={\frac {1}{(a+b)^{\frac {2}{3}}}}\\&={\frac {(a+b)^{\frac {1}{3}}}{(a+b)^{\frac {2}{3}}(a+b)^{\frac {1}{3}}}}\\&={\frac {\sqrt[{3}]{a+b}}{(a+b)^{\frac {2+1}{3}}}}\\&={\frac {\sqrt[{3}]{a+b}}{a+b}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ce316f1ba15dfe32b57cd6a4a76f893e1fb8a42)


![{\displaystyle {\begin{aligned}{\frac {2}{3{\sqrt[{3}]{4}}}}&={\frac {2{\sqrt[{3}]{4}}{\sqrt[{3}]{4}}}{3{\sqrt[{3}]{4}}{\sqrt[{3}]{4}}{\sqrt[{3}]{4}}}}\\&={\frac {2({\sqrt[{3}]{4}})^{2}}{3({\sqrt[{3}]{4}})^{3}}}\\&={\frac {2({\sqrt[{3}]{4}})^{2}}{3\cdot 4}}\\&={\frac {1\cdot ({\sqrt[{3}]{4}})^{2}}{3\cdot 2}}\\&={\frac {({\sqrt[{3}]{4}})^{2}}{6}}\\&={\frac {\sqrt[{3}]{4^{2}}}{6}}\\&={\frac {({\sqrt[{3}]{16}})}{6}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f385b7180390fa3a9f00922c6dc55f5f008a0c04)
![{\displaystyle ({\sqrt[{a}]{b}})^{c}={\sqrt[{a}]{b^{c}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c4f088690d34dad5289bcd294f7dac0b2ba262d)




















