Álgebra Abstracta/Texto Completo
Plantilla:Versión para Imprimir
Primer Curso
Álgebra Abstracta
A. Las Estructuras
[editar]- Nicolas Bourbaki.
- «MacTutor History of Mathematics archive» (en inglés).
- Las definiciones son importantes. Es necesario memorizarlas, reconocer instancias adonde se aplica la definición y distinguirlas de aquellas adonde no se aplican. La memorización debe ser con entendimiento y cada lectora o lector puede redactarlas a su conveniencia, siempre y cuando no cambien el significado.
- Los enunciados validos pueden clasificarse como axiomas, proposiciones, corolarios y teoremas.
Los axiomas son enunciados que aceptamos de partida como válidos. Usualmente en el texto están contenidos en las definiciones. Por ejemplo, cuando estudiamos grupos, suponemos que la operación es asociativa.
Al contrario las proposiciones, corolarios y teoremas son enunciados que deben probarse usando los axiomas u otros enunciados probados anteriormente. Las diferencias entre esos enunciados es énfasis: corolarios son consecuencias inmediatas de una proposición, teoremas son proposiciones con resultados muy importantes (es decir que tienen muchas aplicaciones).
- En cada proposición (o corolario o teorema) es importante identificar claramente las hipótesis (los supuestos) y la tesis (la conclusión). Antes de leer la demostración, resulta valioso intentar pensar en alguno de los ejemplos principales y ver que significa el teorema para esos ejemplos. Igualmente, tratar de buscar una demostración. Algunas proposiciones tienen pruebas relativamente triviales y pueden probarse sin mucho esfuerzo. Aún para aquellas con mayor dificultad, vale la pena intentar la prueba, para poder apreciar mejor la ingeniosidad de la prueba, o ver claramente los puntos principales de la demostración. Al revés de las definiciones, las demostraciones no necesitan ser memorizadas tal cual se presentan. Más importante son los "trucos" usados, que pueden ser usados en otras demostraciones o ejercicios. Después de aplicar los resultados, vale la pena preguntar si no habría otra manera de hacer lo mismo.
- Los ejemplos se presentan para ilustrar propiedades y resultados de proposiciones y, a veces, para motivar o introducir un nuevo concepto. En el último caso, el ejemplo (o ejemplos) será seguido de una definición. Tratar de dar una definición antes de leer aquellas dada en el texto.
Hay ejemplos que se repiten a través del libro, por lo que se debe trabajar con ellos.
- Las demostraciones constituyen, de cierta manera, el meollo del estudio, ya que las demostraciones nos permiten formar una red lógica de conceptos y resultados, que posibilitarán el entendimiento del material. Demostrar es, simplemente, explicar porque creemos que cierta afirmación es válida, la única restricción es que las explicaciones deben ser enunciados previamente conocidos como válidos. Inicialmente, en el texto, hay demostraciones de muchas de las proposiciones, especialmente explicando la razón de cada paso. Posteriormente, tales justificaciones quedarán al cuidado del lector o lectora. Cuando una demostración sea muy extensa o compleja, recomendamos que la lectora o lector trate de dividirla en partes, y examine cuidadosamente lo hecho.
- Asociativa, si, para todo en ,
se cumple que:
- Conmutativa, si, para todo en , se
cumple que:
- Distributiva respecto a otra operación , si, para todo
a, b y c en , se cumple que:
- Evaluate .
- Verificar que is asociativa.
Sean , y tres elementos cualesquiera de .
Lo que prueba la asociatividad.
- Veamos ahora que es conmutativa.
Como la suma de enteros es conmutativa, los pares ordenados a la derecha son iguales, lo que prueba la conmutatividad.
- Dar tres ejemplos de operaciones asociativas.
- Dar dos ejemplos de operaciones no asociativas.
- Definir la operación en los Enteros por . Evaluar , , . ¿Es asociativa? ¿conmutativa?
- Suponer que la operación no es asociativa. Entonces, la expresión tiene dos interpretaciones posibles. ¿Cuántas interpretaciones posibles tiene la expresión ?
- Suponer que la operación es asociativa. Verificar que todas las interpretaciones posibles de la expresión (ver el ejercicio anterior) producen el mismo valor.
- Sea * una operación en el conjunto con neutro . Como tenemos que el elemento neutro es invertible y que es su
- Como cada elemento invertible tiene un único inverso, hablaremos de el
- Sea un elemento invertible. Entonces, su
inverso también tine inverso, que es el elemento original Es decir,
- Sean elementos invertibles, entonces su producto también es invertible y se cumple que
(Notemos el cambio de orden en el lado derecho) Es decir que el inverso de un producto de dos elementos invertibles es invertible y su inverso es el producto de los inversos de los factores pero con el orden cambiado.
- Como y vemos que es un inverso de Por la unicidad de los inversos, debe ser \textbf{el} inverso de .
- Se tiene que
Por la unicidad de los inversos, tenemos el resultado.
- (Terminología) Algunos autores llaman leyes de composición a las operaciones, elementos simetrizables a los invertibles.
- Nuestra definición de operación es aquella de una operación binaria porque asocia a dos elementos del conjunto un valor. Como esas será, en la práctica, la única forma de operación que usaremos, hemos omitido el apellido. Sin embargo podemos definir operaciones con otra cantidad de argumentos. Véase, por ejemplo, el apéndice sobre la Teoría de Estructuras Algebraicas.
- Nuestra definición de operación es aquella de una operación interna. Hay otra clase operaciones llamadas externas en un conjunto E, que son funciones , donde A usualmente tiene también una estructura algebraica. El ejemplo típico de operación externa es el producto de un escalar (número) por una matriz, o de una constante (número) por una función.
- La composición[1] de funciones define una operación asociativa en F(X,X).
- La función identidad que envía cada elemento de X en si mismo, es un neutro para la composición.
- Las funciones inyectivas son cancelables por la izquierda.
- Recordemos que una función es inyectiva, ssi, para todo , ,\\ implica que . Supongamos que son 0funciones tales que y que es inyectiva. Entonces, para todo , en
- Por lo que (toman el mismo valor para cualquier elemento de ).
- Las funciones suprayectivas son cancelables por la derecha.
- Recordemos que una función es suprayectiva, ssi, para todo en, hay un en tal que . Supongamos que son funciones tales que y que es suprayectiva. Entonces, para todo en hay un en tal que .
- Luego, . Por lo que
- Las funciones biyectivas, por ser inyectivas y suprayectivas son cancelables por izquierda y derecha. De hecho, son invertibles.
- Sea el conjunto de números reales de la forma , donde y son números racionales. Probar que la suma y el producto de dos números de esa forma son de la misma forma. Probar que . tiene un recíproco de la misma forma, cuando y no son ambos nulos.
- (Enteros módulo )
- En , con la multiplicación. ¿Cuáles elementos tienen recíprocos?
- En , con la multiplicación ¿cuáles elementos tienen recíprocos?
- Probar que si para un elemento de un magma se cumple que , donde es un neutro. Entonces, es invertible.
- Sea un magma asociativo con neutro . Suponer además que y son elementos invertibles del magma. No suponga conmutatividad.
Simplificar las siguientes expresiones.
- .
- Sea un magma asociativo, pero no conmutativo. Sean , y elementos invertibles de . ¿Cuál es el inverso de ?
- cerrado respecto a la operación cuando el producto de dos elementos de está siempre en .
- cerrado respecto a tomar neutro, cuando contiene al neutro.
- cerrado respecto a tomar inversos, cuando para cada , el recíproco de , también está en .
1. Introducción
[editar]|
" Faire d'Algèbre, c'est esentiellement calculier ... " |
¿Qué es el Álgebra Abstracta?
[editar]El Álgebra Abstracta, como indica su nombre, surge como una abstracción de propiedades algebraicas comunes a diferentes sistemas numéricos y a otros objetos de estudio matemático. La preocupación principal es acerca de las propiedades de las operaciones, independientemente (abstracción) de la naturaleza de los operandos. La suma de los números naturales, así como aquella de los Enteros, de los Reales, o de funciones, o de matrices etc. es asociativa. Lo que interesa aquí es estudiar las consecuencias de suponer que la suma en un conjunto cualquiera (de números o no) sea asociativa.
Hay tres fuentes clásicas para el Álgebra Abstracta: la teoría de las ecuaciones polinómicas, la teoría de los números enteros y la Geometría. Cada una de esas áreas se desarrolló inicialmente de manera independiente de las otras. Con el pasar del tiempo, se observaron muchas semejanzas entre los resultados obtenidos, con lo que se inició la abstracción de dichos resultados. Tal desarrollo se produce desde fines del siglo XVIII hasta el inicio del siglo XX, cuando las nociones adquirieron una forma semejante a lo que expondremos en este texto.
Los trabajos de abstracción contribuyeron a identificar la noción de estructura algebraica como central al estudio del Álgebra. Una estructura algebraica es, básicamente, un conjunto provisto de una o más operaciones que poseen algunas propiedades especiales. La ventaja del enfoque abstracto es que permite al estudiar una estructura, estudiar propiedades de los variados ejemplos de tales estructuras (a veces infinitos ejemplos). En segundo lugar, podemos ver de manera más transparente las relaciones y consecuencias de las propiedades de las operaciones.
Como libro texto para un primer curso, suponemos que los lectores son novatos en la materia, lo que no excluye que pueda ser de provecho para lectores con mayor experiencia en el campo. Por lo anterior, hemos enfatizado en ejemplos y colocado una gran cantidad de ejercicios---que son parte integral del texto. Hemos colocado también comentarios que expanden los contenidos o apuntan a referencias tanto a los orígenes como a las aplicaciones.
¿Por qué darle énfasis a las estructuras? Una primera respuesta es comodidad. Antes de su introducción en el álgebra, la situación parecía relativamente simple, estudiar álgebra era aprender a realizar las operaciones algebraicas con los números. Sin embargo, con la aparición de nuevos objetos matemáticos: funciones, vectores, matrices, permutaciones, etc. aparecieron, también, operaciones con ellos. Una alternativa para el estudio era crear una secuencia de cursos más o menos en el siguiente orden: el álgebra de los reales, el álgebra de los complejos, el álgebra de los polinomios, el álgebra de los vectores bidimensionales, el álgebra de los vectores tridimensionales, el álgebra de las matrices, el álgebra de los enteros--modulo, el álgebra de los cuaterniones, el álgebra de los tensores, etc. La invención de nuevos objetos y de sus operaciones, hacían del álgebra un campo en continua expansión y, adonde, era difícil seguirle el rastro a todos los nuevos objetos. Frente a dicha explosión de objetos, se inventó una clasificación que reducía esas álgebras a unas pocas estructuras que servirían para unificar los estudios. Las estructuras básicas con una operación son: semigrupos, monoides y grupos, con dos o más operaciones: anillos, dominios, cuerpos, espacios vectoriales, módulos y álgebras. Estas estructuras, con algunas subestructuras, permiten organizar los estudios por las propiedades básicas comunes, en lugar de mirar a la naturaleza de los elemento .
Por ejemplo, la estructura de cuerpo presupone un conjunto donde están definidas las cuatro operaciones aritméticas poseyendo las propiedades usuales. Ejemplos inmediatos de esa estructura son: los Racionales, los Reales y los Complejos, así como los Enteros módulo un número primo. En este curso, veremos algunos cuerpos adicionales (hay infinitos ejemplos).
Organización del libro
[editar]El libro está organizado en cuatro partes. La primera parte, que incluye esta introducción, presenta las generalidades acerca de las operaciones y de los tipos de estructuras algebraicas básicas más importantes.
La segunda parte esta dedicada a la estructura de grupo (un conjunto con una operación con una serie de propiedades). Esta estructura es fundamental tanto para las matemáticas como para muchas otras áreas del conocimiento: física, química, programación, etc. Los ejemplos básicos de grupo que veremos son: los grupos cíclicos (provenientes de la teoría de números), los grupos simétricos (provenientes de la teoría de ecuaciones), y los grupos provenientes de la geometría (grupos diedrales).
La tercera parte está dedicada a las estructuras de anillo y cuerpo, que son abstracciones de las propiedades algebraicas de los Enteros y de los Racionales respectivamente.
Los ejemplos básicos de anillos son los Enteros (usuales y algebraicos), los polinomios con coeficientes en un cuerpo. Los cuerpos más importantes serán los numéricos (Racionales, Reales, Complejos) y algunos cuerpos finitos.
Finalmente, la cuarta parte son apéndices que contienen resúmenes de las definiciones y propiedades referentes a las funciones, las relaciones, los sistemas numéricos. En estos apéndices, resumimos nociones y resultados que debería conocer un lector de este texto.
Los lectores atentos podrán darse cuenta que, a veces, hay repeticiones de material. Algunas de esas repeticiones son intencionales, a fin de permitir leer capítulos en forma más independientes.
En el texto, en varias ocasiones, mencionamos a las personas que han tenido un rol en el desarrollo de los temas tratados. Esperamos que el lector lea acerca de ellos. El primer sitio adonde buscar lo anterior es el siguiente enlace de la Universidad de San Andrés de Escocia
Aunque, a veces, no lo pueda parecer, éste es un texto elemental. Hay varios textos más avanzados o equivalentes que aparecen en la bibliografía. Otra fuente de consulta son las bibliotecas en línea.
Sugerencias para el estudio
[editar]Cada disciplina o area de estudio tiene una manera especial de adquirir conocimientos respecto a la misma. En Álgebra Abstracta, se trata de una teoría de las operaciones, lo que implica que la validez de los resultados se tienen que deducir de las propiedades básicas (axiomas). Los lectores deben adquirir el hábito (si no lo tienen con anterioridad) de preguntar por la validez de los enunciados. La intuición que tenemos de manipulaciones de expresiones algebraicas anteriores es, sin duda, muy útil; pero que puede ser perturbadora. Muchos de los resultado conocidos, son válidos en ciertas situaciones, pero no en todas; por ejemplo. hay importantes multiplicaciones que no son conmutativas. Como consecuencia de lo anterior, una relación algebraica tan simple como , no siempre es válida. Precisamente, los análisis de Álgebra Abstracta nos permitirán identificar que es necesario suponer para que la relación anterior sea válida.
Algunos convenios
[editar]Usamos los convenios siguientes de notación y nomenclatura para los principales sistemas numéricos.
| El conjunto de los números naturales. | |
| El conjunto de los naturales positivos. | |
| El conjunto de los enteros. | |
| El conjunto de los racionales. | |
| El conjunto de los reales. | |
| El conjunto de complejos. | |
| El conjunto de los enteros módulo |
En el texto, nos referiremos al conjunto de los números naturales, , como los Naturales; igualmente para los otros conjuntos numéricos.
Las notaciones y nomenclatura acerca de funciones se hallan en el apéndice Las Funciones, mientras que lo referente a relaciones se halla en el apéndice Las Relaciones.
2. Las Operaciones
[editar]Introducción
[editar]En este capítulo, iniciaremos nuestros estudios del Álgebra con las abstracciones de las operaciones usuales. Analizaremos, es decir, consideraremos en forma aislada cada una de las propiedades usuales, para ver claramente las consecuencias de las suposiciones de cada una de esas propiedades. Igualmente, para elementos o subconjuntos destacables.
Cuando estudiamos a los números enteros, nos encontramos con las operaciones de suma, resta y multiplicación. Dichas operaciones poseen varias propiedades interesantes. Hay, además, números y subconjuntos destacados respecto a esas operaciones. Igualmente, tenemos operaciones en los Racionales, Reales y Complejos.
Presentaremos nociones que son abstracciones de esas operaciones y de sus propiedades. Al analizar las propiedades de las operaciones y de elementos destacados como el 0, respecto a la suma, o el 1, respecto a la multiplicación, podremos ver las consecuencias lógicas de la existencia de esas propiedades y elementos.
Definiciones y Ejemplos
[editar]La noción general de operación que veremos es una simple abstracción de las operaciones usuales en los conjuntos numéricos. Consideremos las operaciones de suma, resta y multiplicación. ¿Qué tienen en común esas operaciones? Las tres operaciones mencionadas hacen esencialmente lo siguiente: asocian a un par ordenado de números, otro número.
La diferencia entre esas operaciones reside en el valor asociado. Por ejemplo, al par (5, 3), la suma asocia el 8, mientras que resta asocia el 2 y la multiplicación el 15. Esa observación es la base para la definición abstracta de operación que daremos a continuación.
Definición. (Operación) Una operación en un conjunto es una función
Es decir, una operación en un conjunto es la asignación a cada par ordenado de elementos de E, de un único elemento de E. Cuando es una operación, es costumbre denotar el valor de la función en la pareja (x, y) como , en lugar de , como es lo usual para las funciones.
Simbolizamos a las operaciones por símbolos tales como , etc. Usamos para indicar una operación cualquiera. Muchas veces, por simplicidad, escribiremos ab o en lugar de a * b.
Ejemplo 1.1.
En el conjunto de los Enteros, , tenemos tres operaciones: la suma, la resta y la multiplicación. En el conjunto de los (números) Racionales y los Reales tenemos también operaciones de suma, resta y multiplicación.
Ejemplo 1.2.
Sigue de la definición dada de operación que la resta NO es una operación en el conjunto de los números naturales, ya que no siempre es posible asignar un número natural a la resta de dos números naturales. Por ejemplo, 3 - 5 no es un número natural. Aunque lo anterior es diferente a lo usado cotidianamente, la diferencia permite hacer un trabajo lógicamente más simple
Como no hay división por cero en los Reales, la división tampoco es, de acuerdo a la definición dada una operación en dicho conjunto.
Ejemplo 1.3.
Sea un conjunto no vacío y consideremos el conjunto formado por todas las funciones de ese conjunto en los Reales. Para esas funciones se definen una suma, resta y multiplicación de la siguiente manera.
Este ejemplo aparece en cursos elementales con la restricción de que se supone que X es un subconjunto de los Reales.
Ejemplo 1.4.
Sea un conjunto no vacío y sea el conjunto formado por todas las funciones de en si mismo. La composición de funciones es una operación en .
Ejemplo 1.5.
Sea un conjunto no vacío y sea , el conjunto formado por todos los subconjuntos de . La (re)unión e intersección de subconjuntos son operaciones en .
Definición. (Magma) Llamamos magma a un conjunto E provisto de una operación.
Cuando queramos identificar al conjunto y a la operación, describiremos al magma
como un pareja formada por el conjunto y la operación, .
Por ejemplo, los Enteros con la suma () y los Enteros con la multiplicación (), son ejemplos diferentes de magmas.
Propiedades Especiales
[editar]Las propiedades familiares de asociatividad, conmutatividad y distributividad de las operaciones numéricas se pueden definir para un operación cualquiera. Sin embargo, notemos de partida, que no siempre las operaciones tienen esas propiedades.
Definición. (Tipos de Operaciones) Decimos que una operación * en un conjunto es:
Ejemplo 1.6.
La suma y la multiplicación usual en los conjuntos numéricos son operaciones asociativas y conmutativas. Además, la multiplicación es distributiva respecto a la suma.
Significado de la Conmutatividad. Una operación es conmutativa, cuando el orden en que se realiza la operación no afecta al resultado. La resta, en los Enteros, no es conmutativa ya que, por ejemplo, tenemos que y , y .
Significado de la Asociatividad. La asociatividad nos sirve, cuando está presente, para evaluar el resultado de aplicar la operación a más de dos elementos. En tal situación, debemos agrupar elementos en grupos de a dos para poder evaluar (eso proviene de que nuestras operaciones son binarias, o sea que asocian a dos elementos un tercer elemento). La asociatividad nos dice que podemos agrupar como queramos para la evaluación, sin cambiar el orden de aparición, y el resultado no cambiará.
La resta no es asociativa, ya que 5 - (3 - 2) = 5 - 1 = 4, mientras que (5 - 3) - 2 = 2 - 2 = 0. Esto nos dice que la expresión 5 - 3 - 2 es ambigua, porque el valor de esa expresión dependerá de como agrupemos los operandos. Al contrario, no es ambigua, ya que y .
En general, cuando una operación * es asociativa, para evaluar una expresión tal
como , lo podremos hacer agrupando como
queramos, ya que ambas posibilidades, y
, producirán el mismo valor. Por esa razón, cuando la
operación es asociativa, podemos eliminar los paréntesis.
Ejemplo 1.7.
Definamos una operación en los Enteros, por . Probaremos que es asociativa y conmutativa.
Resolución. Sean a, b y c números enteros cualesquiera. Tenemos que
Por su parte,
Comparando las dos expansiones, concluimos que Es decir que la operación es asociativa.
Veamos ahora la conmutatividad. y Luego, , o sea que la operación es conmutativa.
Ejemplo 1.8.
Sea el conjunto formado por todos los pares ordenados de números enteros. Definamos una operación en por
Ejercicios
[editar]Los Elementos Destacados
[editar]Algunos elementos de un magma tienen propiedades especiales respecto a la operación. Veremos, en esta sección, las nociones de elementos neutros, invertibles y cancelables, que son abstracciones de ciertas propiedades numéricas.
Elementos Neutros
[editar]En muchas situaciones, hallamos elementos de un conjunto que tienen propiedades especiales respecto a una operación. Pensemos, por ejemplo, en el rol del 0 en la suma o en el rol del 1 en la multiplicación.
¿Qué tiene en común esos elementos? Simplemente, que cuando se operan con cualquier otro elemento, siempre producen el otro elemento. Es decir, que para todo número se cumple que y que En forma abstracta, llamaremos neutro a un elemento con esa propiedad.
Definición. (Elemento Neutro) Sea E un magma con operación *. Decimos que un elemento de es un neutro respecto a la operación *, si, para todo se cumple que
Cuando haya un neutro para una operación, diremos que la operación tiene o admite un neutro.
Ejemplo 2.1.
En los conjuntos numéricos, el 0 es un neutro para la suma y el 1 es un neutro para la multiplicación.
Siempre que tenemos elementos destacados, cabe preguntarse ¿cuántos elementos de ese tipo hay? Los ejemplos del 0 y del 1, nos hacen sospechar que tales elementos son únicos. Lo que probaremos que es válido de forma general, o sea, para una operación cualquiera.
Supongamos entonces que y fueran ambos neutros para una misma operación . Para obtener una respuesta, calcularemos de dos maneras diferentes a .
Como es neutro, tenemos que . Pero como es neutro, tenemos que . Luego .
Hemos así probado, nuestro primer resultado abstracto.
Proposición 1. (Unicidad de Neutros) Cuando una operación tiene un neutro, dicho neutro es único.
A menos que se diga lo contrario, será la notación
preferida para denotar a un elemento neutro cualquiera.
Ejemplo.
Consideremos la operación en los Enteros definida por . Vimos en el ejemplo 1.7 que esta operación era asociativa y conmutativa. Aquí, trataremos de determinar si tiene o no un elemento neutro.
Supongamos que tuviera elemento neutro, digamos Entonces, para cualquier número entero tendríamos que
Donde hemos supuesto que Verifiquemos
Es decir que 0 es efectivamente un neutro para la operación
Los Elementos Invertibles
[editar]Cuando trabajamos con la suma de los números enteros, tenemos asociado a cada número el número que es un número con la propiedad de que sumado con el original nos da el neutro. Los recíprocos tienen propiedades análogas respecto a la multiplicación de los números reales, ya que multiplicados con el número original producen el neutro multiplicativo 1. Generalizaremos lo anterior en la siguiente definición.
Definición. (Elemento Invertible) Sea un magma con neutro Decimos que un elemento de es invertible (respecto a la operación), ssi, hay un elemento , al que llamamos un inverso de , y que es tal que
Observación. El neutro es su propio inverso.
Ejemplo 2.2.
Ejemplo 2.3 (Los Enteros).
La Suma en los Enteros tiene neutro 0 y cada elemento tiene un inverso respecto a la suma, , ya que
La Multiplicación tiene neutro 1 y los únicos elementos invertibles son y ---ya que es el neutro y .
Probaremos, a continuación, que cuando la operación sea asociativa, cada elemento invertible tiene exactamente un inverso.
Proposición 2. (Unicidad de los Inversos) Cuando la operación es asociativa, cada elemento invertible tiene exactamente un inverso.
-
Demostración Sean y inversos de
Se tiene entonces que
La proposición tiene la siguiente interesante consecuencia.
Corolario
2.1. Cuando para cierta operación con neutro, hay un elemento que tiene
al menos dos inversos diferentes, la operación no puede ser asociativa.
inverso del elemento. Cuando tenga inverso, simbolizaremos
dicho inverso porLa proposición anterior tiene los siguientes importantes corolarios
Corolario 2.2. Sea * una operación asociativa en un conjunto E.
-
Demostración. Sean y elementos
invertibles.
Interrogante. ¿Por qué fue necesario suponer asociatividad en la proposición anterior?
Ejemplo 2.4.
Recordemos la operación definida en los Enteros por Vimos anteriormente que esa operación es asociativa, conmutativa y tiene neutro 0. Nos preguntamos ahora, ¿cuáles elementos tienen inverso respecto a esa operación?
Resolución. Supongamos que es un número entero con inverso respecto a Entonces,
Lo que prueba que tendrá inverso, ssi, podemos dividir por en los Enteros. Es decir, ssi, o Por lo que o son los únicos posibles elementos invertibles, y sus inversos serían, respectivamente, 0 y Como es el neutro, sabíamos que tenía inverso y que era él mismo. Verifiquemos el caso de
Luego, los únicos elementos invertibles respecto a son el neutro y .
Los Elementos Cancelables
[editar]En los números Enteros, la relación implica que , a pesar de que no hay división por 3 en los enteros. Esa cancelación del 3 se generaliza en la siguiente definición, que habla de cancelación por la izquierda o derecha, ya que las operaciones no son necesariamente conmutativas.
Decimos que un elemento a es cancelable por la derecha, ssi, para todo x, y de E, se cumple que
Decimos simplemente que un elemento es cancelable, cuando lo sea tanto por la derecha como por la izquierda.
Ejemplo 2.5.
En los Enteros, con respecto a la multiplicación, todos los elementos no nulos son cancelables.
Probaremos, a continuación, que cuando un elemento es invertible, ese elemento es cancelable. El recíproco de lo anterior no es cierto como lo muestra el ejemplo de la multiplicación en los Enteros.
Proposición 3. (Invertibles son cancelables) Cada elemento invertible respecto a una operación asociativa es cancelable.
-
Demostración: Sea un elemento invertible con inverso,
digamos, Entonces
Ejemplo 2.6.
Volvemos a examinar la operación del ejemplo 1.8, para determinar elementos cancelables respecto a esa operación.
Resolución: Sean , , enteros cualesquiera.
Es decir que todos los elementos diferentes de son cancelables.
Convenios de notación
[editar]Podemos simbolizar una operación de muchas maneras diferentes, pero hay algunas maneras que usamos más frecuentemente. Por ejemplo, las sumas se simbolizan usando o algo parecido, . Cuando usemos hablaremos de la notación aditiva. Usaremos preferentemente la notación aditiva cuando la operación sea conmutativa. Por su parte, la multiplicación se denota por o nada y diremos que estamos usando la notación multiplicativa. Cuando queramos insistir en la abstracción, usaremos la notación La siguiente tabla resume los convenios notacionales acerca de esas notaciones.
| Si la operación es | + | * | |
|---|---|---|---|
| la notación es | Aditiva | Multiplicativa | General |
| el neutro es | 0 | 1 | e |
| el inverso es | -a | ||
| opuesto aditivo | recíproco | inverso |
Observaciones.
Ejemplo: F(X,X)
[editar]Sea X un conjunto no vacío. Simbolizamos por al conjunto formado por todas las funciones del conjunto X en si mismo. La composición de funciones es una operación en ese conjunto.
Este es un ejemplo importante, que reaparecerá varias veces en el futuro. Ilustra un conjunto con una operación donde hay elementos cancelables que no son invertibles o que son cancelables por la izquierda, pero no por la derecha, etc.
En F(X,X) tenemos funciones inyectivas, suprayectivas, y biyectivas. Se sabe por resultados generales [1] que:
Ejemplo. Los Enteros Módulo m
[editar]Sea un número entero positivo. Llamamos enteros módulo al conjunto denotado por y que está formado por los enteros, pero sujeto a la condición . Las operaciones de suma, resta y multiplicación son aquellas de los enteros son aquellas de los enteros, pero computadas usando la condición indicada.
Por ejemplo, cuando , se tiene que , , , etc. Además, se tiene que , ya que .
Sea un entero cualquiera, dividiendo por se obtiene un cociente y un residuo , , tal que
Por lo que en . Es decir que en hay solamente tantos elementos como residuos en la división por , o sea .
Las operaciones de , por ser las operaciones en los enteros, son asociativas, conmutativas, y la multiplicación es distributiva respecto a la suma
Notemos, que , lo que implica que cada elemento de tiene un opuesto aditivo.
En , el elemento 2 tiene inverso multiplicativo 3, ya que . Como se verá en ejemplos y ejercicios posteriores, no siempre elementos de tienen recíprocos. Por ejemplo en , , , , , lo que muestra que no tiene inverso multiplicativo.
Ejercicios
[editar]Las Partes Cerradas
[editar]Definición. (Cerraduras) Sea E un magma. Decimos que un subconjunto de es:
Ejemplo 3.1.
Sea el magma multiplicativo de los Reales y sea el conjunto de los reales positivos, . Los positivos son cerrados respecto a la multiplicación, al neutro y a tomar recíprocos (inversos multiplicativos).
Operación Restringida.
Cuando un conjunto es cerrado respecto a una operación, dicha operación define por restricción una operación en el conjunto cerrado. Aunque, en rigor, la operación restringida es una operación diferente a la operacíón en todo el conjunto, ya que como función se han cambiado su dominio y codominio, es tradicional usar la misma notación para la operación restringida.
Ejemplo 3.2.
Sea S el conjunto formado por todos los números complejos de la forma donde y . Sean y elementos de S.
- Probaremos que con respecto a la adición S es cerrado respecto a la
operación, al neutro y a los opuestos aditivos.
- . Como la suma de enteros es un entero, tenemos que z + w es un elemento de S, lo que prueba la cerradura respecto a la suma,
- Como , el neutro es un elemento de S
- El opuesto aditivo de Z es , que también es un elemento de S.
- Probaremos que S es cerrado respecto a la multiplicación y al neutro
multiplicativo1; pero, veremos que no es cerrado respecto a tomar recíprocos.
- Como , los productos de elementos en S están en S, o sea que S es cerrado respecto a la multiplicación.
- Como , el neutro 1 está en S.
- Como , el recíproco de es igual a
que no está en S.
Proposición 4. Cuando la intersección de dos partes cerradas no es vacia, dicha intersección es una parte cerrada.
-
Demostración: Sean y partes cerradas
respecto a una operación . Sean ,
elementos de . Como
están en , su producto está en . Análogamente,
su producto está en . Luego, el producto está en .
Tablas de Operaciones
[editar]Cuando el conjunto donde actúa una operación es finito y con relativamente pocos elementos, podemos presentar a la operación como una tabla de la operación, que es un arreglo como el siguiente.
El producto b * c se obtiene en la intersección de la fila que contiene a b con la columna que contiene a c. En esta tabla, b * c = a.
Notemos que la fila y columna de e reproducen la fila y tabla de elementos del conjunto, lo que indica que e es neutro.
Veamos como buscar en la tabla si un elemento tiene inverso, digamos que buscamos el inverso de b. Nos movemos por la fila del b hasta hallar el neutro. Si no hallamos un neutro, eso significa que no hay inverso. En este caso hallamos e (neutro en este caso) en la columna del b, lo que nos dice que b * b = e. Por lo que b-1 = b.
En general, si hallamos x * y = e ( e neutro), antes de concluir sobre inversos, debemos chequear y * x (a menos que haya conmutatividad u otra situación especial, no hay nada que indique que y * x = x* y = e).
Cuando la tabla, como en este caso, es simétrica respecto a la diagonal principal (desde izquierda arriba a derecha abajo), tenemos que la operación es conmutativa.
Ejemplo 4.1. (Las tablas de ).
Sabemos que tiene solamente seis elementos, a saber
Presentamos las tablas de la operaciones como ejemplos de tablas finitas. Queda
de asignación verificar la corrección de las mismas.
Mirando a la tabla de suma o por simple computación) vemos que 2 + 4 =0, o sea que -2 = 4. ¿Qué otros elementos tienen opuestos aditivos? En la tabla de multiplicación vemos que 5*5 = 1, o sea que 1/5 =5. ¿Qué otros elementos tiene recíproco?
Finalmente, observemos que {1,5} es un subconjunto cerrado para la multiplicación.
Productos Múltiples, Potencias
[editar]Los lectores seguramente han visto anteriormente sumatorias de números,
Operaciones Generalizadas. Supongamos que tenemos un magma y una sucesión de elementos de E.
Supongamos que queremos hallar el producto de todos ellos. En el texto, hemos aprovechado la experiencia manipulativa de los lectores para no preocuparnos demasiado de ese asunto. La situación es que, por definición, nuestra operación es binaria por lo que no hay como hallar, sin un convenio previo, el producto de una sucesión con más de dos elementos.
Si tuviéramos tres elementos, digamos a, b y c, podríamos formar producto con los tres de una de las siguientes maneras
Notemos que los paréntesis se usan para agrupar dos a la vez. Cuando la
operación es asociativa, ambas expresiones representan al mismo elemento.
Pero, si la operación no fuera asociativa, ¿cuál de las dos sería el producto de
esos tres elementos?
Cuando hay cuatro elementos, hay muchas más posibilidades de agrupamientos, dos a la vez.
Definiremos una noción análoga a las sumatorias para un producto de una sucesión cualquiera.
Definición. (Producto Generalizado) Sea <E,*> un magma y sea . Llamamos producto de los elementos de la sucesión (en el orden indicado) al elemento de E, denotado por y definido como
Es fácil ver, por inducción, de que efectivamente se ha definido un elemento de E.
Sigue de la definición que
- ()
- ()
- () .
Notemos que la definición no requiere que la operación sea asociativa. Cuando la operación sea asociativa, se puede probar que podemos reagrupar como queramos los elementos de la sucesión. Por ejemplo,
Cuando la operación sea además conmutativa, el producto multiple es el mismo para cualquier permutación (reordenamiento) de los índices.
Cuando la operación tenga neutro , se acuerda que el producto de una sucesión vacía es igual al elemento neutro.
En notación aditiva, la definición anterior es la usual definición de sumatoria
Asociatividad. Cuando la operación es asociativa, se puede probar que independiente de la manera que agrupemos los elementos de la sucesión--siempre y cuando, mantengamos el orden de aparición---el producto siempre es el mismo.
- La demostración consiste en considerar particiones de [1,..,n] que preserven el orden y mostrar que el producto de es igual al
producto de los productos parciales.
- Por ejemplo, en el caso si tenemos 1,2|3,4,5|6,7. Entonces
deberíamos probar que , donde Es decir que
- La demostración formal procede por inducción sobre n. Los lectores
experimentados con este tipo de demostraciones puede intentarlo por su cuenta. La demostración formal se puede hallar en las referencias bibliográficas [2], [3] o [4].
También en la página Semigrupos, Monoides,... de WikiLibros, donde puede hallarse demostraciones tanto de la asociatividad como de la conmutatividad generalizadas.
Al igual que hay sumatorias de la forma , podemos definir productos multiples de sucesiones de elementos cuyos subíndices sean un subconjunto ordenado finito de . Dejaremos al cuidado de lectores y lectoras tales generalizaciones.
En cursos primeros de matemáticas, se define la potencia natural de un número como el producto de consigo mismo veces, denotado por . Usando la definición de producto multiple definiremos como el producto de factores, todos ellos iguales a .
Definición. (Potencia) Sean una operación en el conjunto , un elemento de , y un natural positivo. Definimos como el producto , cuando . Cuando la operación tiene neutro , se define, además,
Observación. Sigue de la definición que , .
Proposición ## (Propiedades de las Potencias)
Sea una operación asociativa en , y elementos de , y naturales positivos.
- .
- .
- Si , .
- Si , .
- Si la operación tiene neutro , las relaciones anteriores son válidas para naturales cualesquiera. Además se cumple que , para todo natural.
Demostración Aprovechando la observación anterior, usaremos inducción sobre para las pruebas.
- () . Suponiendo que
. - . Suponiendo que .
. - . Suponiendo que ,
. - . Suponiendo que , .
- Ejercicio.
Ejercicios del Capítulo
[editar]- Completar los espacios en blanco
- Una operación en un conjunto E es una función de _________ en _____.
- Un elemento neutro de una operación * de un conjunto E es un elemento e tal que para todo x en E se cumple que ______________ y ______________ .
- Un elemento x es un inverso de un elemento y, ssi, __________ y ________.
- Un conjunto S es cerrado respecto a una operación, cuando para cada par x, y de elementos de S se cumple que __________________
- Cuando el orden de los operandos no altera el resultado (producto) de una operación, la operación es ________________.
- Cuando la notación es aditiva, el neutro usualmente se simboliza por __.
- Cuando la notación es aditiva, llamamos _____________ ______________ al inverso.
- ¿Cuáles de las siguientes especificaciones determinan una operación en el
conjunto de los naturales positivos, ? En caso afirmativo,
determinar las propiedades de las operaciones y la existencia de neutro y de
inversos.
- .
- máximo común divisor de a y b.
- mínimo común divisor de a y b.
- .
- Construir la tabla de (enteros módulo 2) y respecto a la suma.
- Construir la tabla de (enteros módulo 5) respecto a la multiplicación. Mirando la tabla determinar el neutro y los elementos que tienen recíproco.
- Cada una de las siguientes tablas es una tabla de un operación asociativa.
Examinando la tabla determinar si hay elementos neutros y cuáles elementos tienen inversos.
- Escribir en forma precisa el procedimiento para determinar
en una tabla de una operación
- ¿cuál es el elemento neutro?
- ¿cuáles elementos tienen inversos?
- ¿Cuáles de los conjuntos siguientes son cerrados respecto a la adición en
los Enteros?
- El subconjunto formado solamente por el 0, .
- Los múltiplos de 9.
- Los múltiplos de 23.
- Generalizar los ejercicios anteriores.
- .
- Los Enteros positivos.
- Los Primos.
- ¿Cuáles de los conjuntos siguientes son cerrados respecto a la multiplicación
en los Enteros?
- Los números pares.
- Los números impares.
- Los múltiplos de 5.
- Los Enteros positivos.
- Los Enteros negativos.
- ¿Cuáles de los conjuntos siguientes son cerrados respecto a la adición en
los Racionales?
- Los Racionales positivos.
- Los Racionales negativos.
- Los números de la forma , donde m es un entero cualquiera y n es un número natural.
- Los números de la forma donde m es un entero positivo y n es natural.
- Probar que el conjunto , donde , es cerrado respecto a la multiplicación en los Complejos. Construya la tabla correspondiente a esa operación,
- Sea A una parte cerrada respecto a una operación. Explicar por qué cuando operación es asociativa (resp.conmutativa), su restricción a A también lo será.
- Sea el conjunto formado por todos los números reales de la forma donde y son racionales. Probar que es cerrado respecto a la multiplicación en los Reales.
- Sea X un conjunto y sea el conjunto formado por todos los subconjuntos de X. Investigar si la unión e intersección de subconjuntos son operaciones y sus propiedades.
- Sea E un magma. Decimos que dos elementos a y b permutan o conmutan entre si, ssi, ab = ba. probar que si la operación es asociativa y a conmuta con b y c, entonces, a conmuta con b * c.
- ¿Cuántas operaciones diferentes se pueden definir en un conjunto con dos elementos?, ¿cuántas son conmutativas?
Notas
[editar]3. Las Estructuras Algebraicas
[editar]Introducción
[editar]Cuando a un conjunto lo proveemos de una o más operaciones, obtenemos una estructura algebraica. En este capítulo, veremos algunas de las estructuras clásicas con una o dos operaciones.
Las estructuras se clasifican por la cantidad de operaciones que aparecen en la estructura, las propiedades de esas operaciones, la existencia de elementos o subconjuntos destacados y las relaciones (de orden u otras) entre los elementos del conjunto base.
Presentaremos diversos tipos de estructuras con ejemplos de cada uno de esos tipos. Resultará importante familiarizarse con esos ejemplos, ya que nos referiremos a la mayoría de ellos en capítulos posteriores.
Estructuras Algebraicas
[editar]Una Estructura Algebraica o Sistema Algebraico es un lista de la forma <E, p1, p2 , ...> donde E es un conjunto (llamado el conjunto base o portador de la estructura) y p1, p2 , ... son los parámetros de la estructura. Dichos parámetros son usualmente operaciones en E, incluyendo operaciones externas (operaciones tales como la multiplicación por constante de una función, o escalar por matriz). También puede haber relaciones entre los elementos de E.
- Las operaciones pueden ser de varios tipos. Además de las operaciones vistas en el capítulo anterior, que son operaciones binarias porque tienen dos operandos, hay operaciones unarias, ternarias, etc.
El Álgebra Abstracta es el estudio de las diferentes estructuras---definiciones, propiedades, relaciones entre ellas, etc--- independiente de la naturaleza de los elementos del conjunto base. Como veremos en el texto, varios conjuntos diferentes sirven de conjunto base de una misma estructura. A medida que avancemos en el texto, discutiremos más detalles acerca de las estructuras. Una discusión más detallada puede hallarse en el apéndice sobre la Teoría de Estructuras Algebraicas.
Estructuras con una Operación
[editar]
Nuestro estudio empezará con estructuras muy simples ya que la lista de parámetros incluye solamente a una operación. Veremos las estructuras de magma, semigrupos, monoides y grupos. [1]

Definición de Magma
[editar]La estructura algebraica más simple que consideraremos, magma, fue introducida en el capítulo anterior. Recordaremos a continuación su definición.
Definición. (Magma) Llamamos magma a un par <E,*> donde E es un conjunto no vacío y es una operación en el conjunto.
Ejemplos.
- Los Enteros con la suma, , o con la multiplicación, .
- Los Racionales, los Reales, los Complejos con respecto a la suma y también a la multiplicación.
- Los Enteros con la resta.
Sea <E,*> un magma. Cuando no haya ambigüedad acerca de la operación de un magma, podremos hablar simplemente del magma E. Otras veces, podremos hablar del magma E con la operación *.
Definiciones de Semigrupo, Monoide y Grupo
[editar]Definición. (Semigrupo, Monoide, Grupos)
- Un semigrupo es un magma con operación asociativa.
- Un monoide es un semigrupo con elemento neutro.
- Un grupo es un monoide cuyos elementos son todos invertibles respecto a la operación.
Ejemplos.
- Los Enteros con la resta forman un magma que no es un semigrupo, ya que la resta no es asociativa.
- Los Naturales positivos con la suma forman un semigrupo (la suma es asociativa) que no es un monoide, ya que el neutro 0 no está en el conjunto.
- Los Naturales con la suma forman un monoide que no es grupo, ya que los opuestos aditivos de los naturales positivos no están en el conjunto.
- Los Enteros con la suma forman un grupo abeliano.
- Los Racionales, Los Reales y los Complejos, con la suma determinan grupos abelianos.
- Los Racionales, los Reales y los Complejos no nulos, con la multiplicación usual, determinan grupos abelianos.
Observaciones acerca de las estructuras y de la terminología asociada.
- En rigor, debiéramos decir, por ejemplo, que "tiene o posee una estructura de grupo", o que es una "instancia de la estructura de grupo", pero simplemente decimos es un grupo o hablamos del grupo (aditivo) de los Enteros.
- En rigor, deberíamos especificar a un monoide como (que tiene) una estructura para indicar la existencia del neutro e. Igualmente, un grupo debiera especificarse como para indicar que hay, además, inversos para cada elemento. Sin embargo, cuando no haya riesgo de confusión mencionamos solamente el conjunto, la operación y el tipo de estructura.
- (Descendientes, Ascendientes, Subyacentes) Observemos que hemos definido a las estructuras magma, semigrupos, monoides y grupos, como que cada una es un caso especial de la anterior. Decimos que una estructura es descendiente de una segunda estructura, cuando sea un caso especial de la otra. En tal situación, decimos que la segunda estructura es un ascendiente de la primera. Por ejemplo, las estructuras de semigrupos, monoides y grupos son descendientes de la estructura de magma. Cuando una estructura es descendiente de otra, podemos ignorar lo que la hace distinta de la segunda, y decimos que tiene una estructura \textit{subyacente} del tipo de la segunda. Por ejemplo, el grupo , o sea, tiene una estructura subyacente de monoide (nos olvidamos de los opuestos aditivos). También tiene una estructura subyacente de semigrupo, . Cuando una estructura es descendiente de otra, podemos ignorar lo que la hace distinta de la segunda, y decimos que tiene una estructura \textit{subyacente} del tipo de la segunda.
- (Herencia) La razón de llamar descendientes a las estructuras especiales es para señalar que las propiedades de una estructura son heredadas por sus descendientes.
En Álgebra Abstracta, se prefiere siempre enunciar y probar los enunciados en la estructura más general posible, para que sirva para todos sus descendientes.
Sigue de la observaciones anteriores que todas las propiedades de magmas probadas en el capítulo anterior son válidas para semigrupos, monoides y grupos.
Propiedades de Monoides
[editar]Un monoide puede contener elementos invertibles, aunque no sea un grupo. Por ejemplo, los Enteros no nulos con la multiplicación forman un monoide que no es grupo, ya que los enteros diferentes de 1, -1 no tienen recíprocos. Sin embargo, 1 y -1 tienen inversos que son ellos mismos. Esto implica que el conjunto U = {1,-1} determina con la multiplicación un grupo. La situación es bastante general, como lo muestra la siguiente proposición.
Proposición 1. (Grupo de invertibles de un Monoide) Sea <M,*> un monoide y sea UM el conjunto formado por todos los elementos de M que son invertibles. Entonces < UM, *> es un grupo.
-
Demostración: Como el producto de invertibles es invertible, UM es cerrado respecto a la operación, por lo que la restricción de la operación a UM define allí una operación. El neutro siempre es invertible, por lo que el neutro es un elemento de UM. Finalmente, los inversos de elementos invertibles son invertibles, por lo que cada elemento de UM tiene inverso en UM. Es decir que < UM, *> es efectivamente un grupo.
Ejemplos.
- Los Reales con la multiplicación forman un monoide cuyo grupo de invertibles esta determinado por los Reales no nulos. Igualmente, para los Racionales y los Complejos.
- Las matrices cuadradas con la multiplicación forman un monoide, cuyo grupo de invertibles, está formado por las matrices invertibles.
Orden de un Elemento
[editar]Definición. (Orden de un Elemento) Sea un monoide (o grupo) con neutro y un elemento de , Cuando haya un número natural positivo tal que , llamaremos orden de al menor entero positivo con esa propiedad. Cuando el conjunto de potencias de un elemento consista de elementos diferentes entre si, diremos que el elemento tiene orden infinito. Notación: .
Ejemplos.
- El número imaginario es tal que . Por lo que su orden es 4.
- En un grupo aditivo, los múltiplos son las potencias. Por lo que un elemento a tiene orden finito n, cuando na = 0. En los Enteros, no hay números n positivos tales que , por lo que el orden de 1 es infinito. En los Enteros módulo m, todos los elementos tienen orden finito respecto a la adición.
Proposición 2. Sea a un elemento de un monomio M con , o sea, tal que hay un entero positivo n tal que Entonces, a es invertible con inverso
-
Demostración:
Ejemplos.
- En los Enteros Luego, es invertible y su inverso es ,
- E los Entremos módulo 5, se tiene que . Luego, 2 tiene recíproco allí. Su recíproco es
Ejemplos
[editar]El Álgebra Abstracta como su nombre lo indica tiene su origen en la abstracción de propiedades de ejemplos existentes. Esta (relativamente larga sección, quiere mostrar algunos de esos ejemplos). Es importante que los lectores se familiaricen con ellos. Deben procurar, además, identificar las nociones vistas en el capítulo anterior: elementos neutros, invertibles, cancelables, partes cerradas.
Los Sistemas Numéricos
[editar]Nuestros sistemas numéricos son los Naturales, Enteros, Racionales, Reales y Complejos. A ellos siempre agregaremos los Enteros módulo cierto número.
Los principales resultados que el lector deberá examinar cuidadosamente para ver la validez de lo afirmado.
- <X, +> es un grupo abeliano, cuando
Las relaciones de inclusión entre esos conjuntos producen subestructuras. (cuya definición formal veremos posteriormente). Como se trata de la misma operación, el mismo neutro y los mismos opuestos, decimos que los Enteros son un subgrupo aditivo de los Racionales (y de los Reales y de los Complejos). Igualmente, los Racionales son un subgrupo de los Reales y Racionales. Finalmente Los Reales forman un subgrupo de los Complejos. - <X*, > es un grupo abeliano cuando X* indica los elementos no nulos de X.
- Los Enteros módulo m son un grupo respecto a la adición. Con respecto a la multiplicación, sus elementos no nulos, en general, forman un monoide.
El Grupo Simétrico
[editar]En el capitulo "Las Operaciones" destacamos al ejemplo formado por todas las funciones de en si mismo. Vimos que dicho conjunto con la composición de funciones tiene una estructura de monoide. Por lo tanto, de acuerdo a la proposición 1, los elementos invertibles de dicho conjunto determinan con la composición un grupo al que llamamos el grupo simétrico de y que denotamos por . Notemos que los elementos invertibles de son las funciones biyectivas de en si mismo. Se puede verifica que cuando el conjunto tiene más de dos elementos, dicho grupo no es conmutativo.
Cuando es el conjunto formado por los primeros números naturales positivos, denotamos a por y le llamamos grupo de las permutaciones de n símbolos o grupo simétrico de grado n. Una permutación, en este contexto, es una función biyectiva de cualquier conjunto finito en si mismo.
Grupo de Permutaciones En forma general, llamamos grupo de permutaciones a un grupo G, tal que G es un subconjunto de algún . Históricamente, estos fueron los primeros grupos estudiados.
Representación matricial de permutaciones. Cuando sea una función de In en si mismo, escribiremos la tabla de valores de la función de la siguiente manera
Por ejemplo, todas las biyecciones de en si mismo son:
Las permutaciones están asociadas, usualmente, con reordenamientos. Mirando a la segunda fila, vemos porque llamamos permutaciones a esas funciones. La siguiente tabla muestra los resultados de la composición de esas funciones, es decir la tabla del grupo.
Mirando la falta de simetría respecto a la diagonal principal, vemos que la operación no es conmutativa. Claramente, f0 es la identidad (como función) que es el neutro del grupo.
¿Cómo obtuvimos los resultados? Simplemente por composición de funciones. Veamos el cómputo de
Luego, el producto es igual a f1
¿Cuántos elementos tiene ?
Razonando como reordenamiento de In, vemos que debemos ubicar los n elementos de ese conjunto en n posiciones. Tenemos n posibilidades para la primera posición, (n-1) para la segunda, (n-2) para la tercera, etc. Luego,
|
|
Las Matrices 2 x 2
[editar]Denotamos por al conjunto formado por todas las matrices 2 x 2 con entradas o componentes números reales. Hay operaciones de suma y producto de matrices que recordamos a continuación.
Dichas operaciones tienen las propiedades que indicaremos a continuación. La verificación de la validez de las mismas queda al cuidado de los lectores.
- La suma de matrices es asociativa, conmutativa, tiene neutro y cada matriz A tiene opuesto aditivo -A. Lo que nos dice que las matrices con la suma determinan un grupo abeliano.
- La multiplicación de matrices es asociativa, pero no conmutativa. Tiene neutro . Por lo que las matrices con la multiplicación determinan un monoide. Las matrices con la multiplicación no determinan un grupo, porque no todas las matrices no nulas tienen inverso. En, efecto se sabe que únicamente las matrices con determinante no nulo son invertibles. Se sabe que si la matriz
tiene determinante (ad- bc) no nulo, su inversa es
Las matrices invertibles determinan un grupo ya que el producto de invertibles es invertible con inversa igual al producto de las inversas de los factores, pero con orden invertido.
y la inversa de una matriz invertible tiene como inversa a la matriz original.
Dicho grupo se llama grupo lineal (de dimensión 2) sobre los Reales y se denota por .
Ejercicios
[editar]- Verificar la validez de las afirmaciones sobre las propiedades de las operaciones con matrices.
- Para cada uno de los siguientes conjuntos de matrices, investigar si son cerrados respecto a la multiplicación, si la identidad pertenece al conjunto y si el inverso de cada elemento en el conjunto pertenece al conjunto
- Sea el subconjunto formado por todas las matrices invertibles cuyas entradas son todas números racionales. Probar que dicho conjunto con la multiplicación tiene una estructura de grupo.
- Sea el conjunto de matrices de la forma
Probar que las matrices no nulas de forman un grupo con la multiplicación.
Los Enteros módulo m
[editar]En esta sección, construiremos de manera formal el conjunto de los Enteros módulo , así como sus operaciones de adición y multiplicación. Esta construcción servirá de modelo más adelante en la construcción de los llamados grupos cocientes.
Definición. (Congruencia módulo m en los Enteros) Sea m un entero positivo. Decimos que dos enteros x, y son congruentes módulo m, ssi, x - y es un múltiplo de'm
Notación: o
Claramente, esa relación es reflexiva y simétrica. Probaremos la transitividad.
Luego , lo que prueba la transitividad. Nos referiremos a esta relación como la congruencia módulo m.
Supongamos que tenemos una relación de equivalencia en un conjunto $X$. Llamando clase de equivalencia de un elemento $x$ al subconjunto formado por todos los elementos relacionados con $x$ y que denotamos por $x$, se sabe que dichas clases forman una \text it{partición} del conjunto $X$. Es decir que son disjuntas dos a dos y que su (re)unión es todo $X$. Ver los detalles en el apéndice \ref{chRelaciones}.
Las clases de equivalencia con respecto a la relación de congruencia se llaman también clases de congruencia. La clase de congruencia módulo de un número está formado por todos aquellos números tales que es un múltiplo de , o sea tales que , para algún .
Simbolizaremos por al conjunto formado por todas las clases de equivalencia módulo y diremos que sus elementos son los \textit{enteros módulo }. Cada elemento de una clase es un \textit{representante} de la clase. Simbolizaremos por el conjunto formado por todas las clases de equivalencia módulo m y diremos que sus elementos son los Enteros módulo m. Cada elemento de una clase es un representante de la clase.
Ejemplo (Enteros módulo 2).
En este caso dos elementos son equivalentes, o lo que es lo mismo definen la misma clase de equivalencia cuando su diferencia es un múltiplo de 2 (o sea un número par). Por lo que la clase del 0, [0] está formado por todos los x tales que x - 0=x es un número par, por lo que la clase del 0 está formada por todos los números enteros pares.
Por su parte, la clase del 1, está formada por enteros cuya diferencia con 1 sea par, o sea los impares.
Luego, ,
Ejemplo (Enteros módulo 5).
En este caso, dos números son equivalentes cuando su diferencia es un múltiplo de 5. Construyamos las clases de equivalencia. La clase del 0 está formado por todos aquellos números cuya diferencia con 0 es un múltiplo de 5, o sea todos los múltiplos de 5.
Busquemos ahora la clase de equivalencia del 1. Como , ssi, , ssi, . La clase del [1] estará formada por todos los enteros que son 1 más que un múltiplo de 5.
Análogamente, obtenemos que
Notemos que , etc. Es decir que hay solamente cinco clases diferentes.
|
|
Operaciones en .
Queremos definir operaciones de suma y multiplicación en por
Es decir que la suma de la clase de x con la clase de y sea la clase de x+y y análogamente para la multiplicación. Hay, sin embargo, un problema con tal definición. La suma (y, lo mismo, el producto) se obtienen sumado (resp. multiplicando) dos representantes, uno de cada clase; por lo que resulta natural preguntar, ¿qué pasaría si escogiéramos otras representantes? La siguiente proposición no asegurará que no importa los representantes que escojamos, siempre obtendremos el mismo resultado.
Proposición 3. (Compatibilidad con las operaciones) Sean a, b, c, d números enteros tales que y Entonces,}}
- .
-
Demostración. Tenemos que
, para algún .
, para algún .
Luego, como
tenemos que , lo que prueba la parte a.
Para la multiplicación, tenemos que:
Es decir que .
Corolario. Suponer que y que Entonces,
El grupo aditivo de los Enteros módulo m
[editar]Veremos que con suma forman un grupo abeliano.
Necesitamos verificar que la suma es asociativa, conmutativa, con neutro y que cada elemento tiene un opuesto aditivo.
Sean números enteros.
Lo que prueba la asociatividad.
, lo prueba conmutatividad.
Claramente, , lo que muestra que la clase del 0 es el elemento neutro.
Finalmente, para cada , tenemos que , lo que prueba que Es decir cada elemento tiene un opuesto. Esto concluye la prueba.
El monoide multiplicativo de los Enteros módulo m
[editar]Veremos que los Enteros módulo m con la multiplicación forman un monoide. La asociatividad y la conmutatividad se prueban de manera análoga al caso de la suma. Además, , por lo que [1] es un neutro.
Se puede verificar que cuando m es un número primo, , los elementos no nulos de , forman un grupo abeliano respecto a la multiplicación. Cuando m es compuesto aparecen unas cosas raras en la multiplicación. Por ejemplo, en , la clase del 2 y la clase del 3 son distintas de la clase del 0, ya que ninguno de ellos es un múltiplo de 6, pero . Dos elementos no nulos al multiplicarse producen el elemento nulo.
Ejercicios
[editar]- Construir las tablas de operaciones (adición y multiplicación) de
Usar la tabla para evaluar las expresiones siguientes.
a. [7]+ [2] b. [8]*[5] c. -([3]*[6]) d. 1/[3] e. 1/[5] f. 1/[7] - Hallar los cuadrados y los cubos de todos los elementos de .
- Hallar los recíprocos de todos los elementos no nulos de .
- Resolver la ecuación en .
- Resolver en , el sistema de ecuaciones
Estructuras algebraicas con dos operaciones
[editar]Las estructuras con dos operaciones, que veremos a continuación, puede que tengan un sabor más familiar. Por ahora, sin embargo, su aparición se debe a que nos proveen de ejemplos de las estructuras con una operación. Las estructuras con dos operaciones se verán detalladamente en capítulos posteriores.
Definición (Anillos, Cuerpos) Un anillo es un trío tales que
- es un grupo abeliano (grupo aditivo del anillo).
- es un semigrupo (semigrupo multiplicativo del anillo.
- La multiplicación es distributiva respecto a la adición.
y ,
Un anillo con identidad es un anillo con un neutro 1 para la multiplicación (llamado identidad del anillo). Un anillo conmutativo con identidad es un anillo con la multiplicación conmutativo y con un neutro 1 (llamado identidad del anillo)
Un cuerpo es un anillo conmutativo con identidad donde cada elemento no nulo tiene recíproco.
Los Enteros son un ejemplo de anillo conmutativo con identidad. Los Racionales, Reales y Complejos serán, por ahora, nuestros ejemplos de cuerpos.
Proposición 4. Cuando p es un número primo, los Enteros módulo p son un cuerpo.
-
Demostración: Vimos anteriormente que para cualquier los Enteros módulo m está provisto de operaciones de suma y multiplicación definidas por
| . |
Es fácil ver que con esas operaciones, es un anillo conmutativo con identidad.
Probaremos que cuando p es un número primo, los elementos no nulos de .
El resultado sigue de la identidad de Bezout para los números enteros que establece que el máximo común divisor de dos números se puede expresar como una combinación lineal de los números [3].
Si es un elemento no nulo de , el número a no pude ser n múltiplo de p, por lo que el máximo común divisor de a y p debe ser 1. Luego, por la identidad de Bezout, hay enteros x, y tales que
| (*) |
Pasando a clases de equivalencias, tenemos que
Lo que muestra que tiene a como recíproco. {{QED}
Matrices con entradas en un anillo
[editar]Queremos aumentar nuestro caudal de ejemplos, definiendo matrices con entradas en un anillo con identidad o cuerpo cualquiera. Notemos que las definiciones de suma y multiplicación de matrices con entradas reales lo único que requieren de los Reales es que se pueden sumar y multiplicar. Como esto pasa en cualquier anillo, podemos considerar matrices cuyas entradas pertenecen a un anillo cualquiera.
Sea A un anillo con identidad o un cuerpo. Simbolizaremos por el conjunto de todas las matrices 2 x 2 cuyas entradas son elementos de A. Es un ejercicio largo, pero fácil, probar que <math<M_2(A)</math> con esas propiedades determina un anillo con identidad. El anillo no es conmutativo.
Se define el determinante de como es usual, esto es . Se verifica que
Sea K un cuerpo, por simbolizamos al grupo de matrices invertibles con entradas en K. Cuando K sea los enteros módulo p, p primo, es un grupo finito, que se prueba que tiene elementos.
Ejercicios
[editar]- Probar que es un anillo conmutativo con identidad.
- Probar que cuando m no es un número primo, en hay elementos no nulos tales que
- Probar que las matrices 2 x 2 con coeficientes en un anillo conmutativo con identidad determinan un anillo con identidad, pero que no es conmutativo.
- Sea . Probar o verificar las siguientes afirmaciones.
- Si una de las filas o una de las columnas de la matriz es 0 0 , entonces el determinante es cero.
- Si hay un número p tal que c = pa y d = cb entonces el determinante de la matriz es cero.
- Si el determinante de A es cero, probar que hay un número p tal que c=pa y d = pb.
- Usar el ejercicio anterior para hallar la formula para la cantidad de elementos de , p primo. (Sugerencia. Cualquier par de elementos que no sean ambos nulos sirven para la primera fila. ¿Cuántos pares de elementos hay que no sean ambos nulos? La segunda fila no puede ser un múltiplo de la primera, por lo que hay que tomar un par de elementos que no sea un múltiplo de la primera fila ¿cuántos de esos pares hay?)
Estructuras con una operación externa
[editar]Presentaremos, como ilustración, algunas estructuras donde aparece una operación externa.
Definición (Módulo, Espacio vectorial, Álgebra)
- Sea A un anillo con identidad. Llamamos A--módulo a un grupo abeliano <E,+> provisto de una operación externa
que es compatible con la estructura de grupo abeliano. Es decir que- .
- .
- .
Los elementos del anillo se dice que son los escalares y los de E los vectores. La operación externa se llama multiplicación por escalar y usualmente, cuando no hay riesgo de confusión, se omite el símbolo de la operación.
- Un Espacio vectorial sobre un cuerpo K, es un K-módulo (o sea los escalares forman un cuerpo).
- Un Álgebra sobre un anillo (o cuerpo) A es un A-modulo E provisto de una multiplicación tal que es un anillo y se cumple que
.
Los principales ejemplos que posiblemente el lector debe conocer:
- El álgebra de polinomios, la multiplicación por constantes es la operación externa.
- El álgebra de matrices, la operación externa es la multiplicación por escalar (por constante).
- El plano cartesiano es un espacio vectorial sobre > los elementos del plano son pares ordenados de números reales, la suma se hace coordenada a coordenada y la multiplicación por escalar, es multiplicar cada coordenada por el escalar.
| . |
Claramente, las definiciones anteriores se pueden extender a (Espacio vectorial d dimensión n).
El álgebra de polinomios tiene un capítulo en este texto. Espacios vectoriales, Algebras son materias de un curso de Álgebra Lineal. Módulos generales se estudian en cursos avanzados de Álgebra Lineal o de Álgebra Conmutativa.
Una introducción a esos temas se puede hallar en Wikipedia:Vector o Espacio Vectorial
Ejercicios del Capítulo
[editar]- (Potencias Naturales en un Semigrupo.)
Probar que para todo a, elementos de ,y , naturales, se cumple que
- Si entonces
- (Potencias en un Monoide.) Si tiene un neutro entonces definimos Probar que con estas definiciones, se continúan cumpliendo las propiedades del ejercicio 1.
- (Potencias Negativas.) Sea <M,*> un monoide y sea a un elemento invertible de cualquiera de S. Como S es un monoide, an está definido, según los ejercicios anteriores, para todo Cuando a es invertible, podemos además definir potencias con exponentes negativos. Supongamos que a' es el inverso de a y n un número entero positivo. Entonces,
- Probar que a elevado a -1 es igual al inverso de a; lo que prueba que la notación a-1 no es ambigua.
- Probar que para todo m, n enteros se cumplen las relaciones del ejercicio 1.
- Sea S un semigrupo con neutro Sea a un elemento de tal que y 12. es el menor entero positivo con esa propiedad. Probar las siguientes afirmaciones.
- Hay elementos y tales que
- Si es un múltiplo de 12, entonces
- Si el residuo de la división de un entero positivo m por 12 es r, entonces
- Expresar como potencias positivas de a.
- (Subgrupos del grupo ).
Sea una rotación por 120 grados, y sea , la reflexión entorno al eje X. Probar las afirmaciones siguientes.- , y .
- Sea . H es un conjunto cerrado respecto a la multiplicación de matrices (construir la tabla de operaciones), y que cada elemento de es invertible. Es decir que H es un grupo respecto a la multiplicación de matrices.
- Sea . G es un conjunto cerrado respecto a la multiplicación y cada elemento de G tiene inverso en G. Luego G es un grupo respecto a la multiplicación de matrices.
Comentarios
[editar]La evolución del Álgebra desde el estudio de ecuaciones polinómicas al estudio de las estructuras fue lenta. Primeramente, se estudiaron instancias de forma separada, para posteriormente darse cuenta que eran ejemplos de algo más abstracto.
La observación de que el Álgebra trata más de las propiedades de las operaciones que de los números en que se opera fue explícitamente observado por la llamada Escuela de Algebristas ingleses, alrededor del 1840.
Finalmente, en la década de los 40 del siglo XX, Bourbaki (seudónimo de un grupo ilustre de matemáticos) trajo a primer plano del Álgebra la noción que el Álgebra se trataba del estudio de las estructuras.
Notas
[editar]B. Los Grupos
[editar]- (i) G es un conjunto,
- (ii) * es una operación asociativa en G;
- (iii) e es un elemento neutro para la operación *;
- (iv) es una función de en que asigna a cada elemento un elemento que es un inverso de respecto a la operación.
- Decimos que un grupo es abeliano[2] o conmutativo cuando la operación es conmutativa.
- Llamamos orden del grupo a la cantidad de elementos del conjunto y lo simbolizamos por
- Decimos que el grupo G es finito cuando su orden lo sea. En caso contrario, es un grupo infinito.
- Los Enteros con la Adición.
Se trata del grupo que es infinito y abeliano. Este grupo nos servirá de motivación e ilustración para muchas nociones que veremos más adelante.
Otros ejemplos numéricos posibles son:
- Los grupos aditivos de los Racionales, los Reales y los Complejos.
- Los grupos multiplicativos de (Racionales, Reales, Complejos no nulos).
- El grupo aditivo de los Enteros módulo m, donde m es un entero cualquiera.
- El grupo multiplicativo de los Enteros módulo p, cuando p es un entero primo.
- Todos esos grupos son abelianos. Los dos últimos son finitos.
- El Grupo Simétrico, Sn. Este grupo está formado por todas las biyecciones del conjunto
In = {1, 2, ... , n} en si mismo. La operación es la composición de funciones. Cuando n >2, el grupo no es conmutativo. - (Grupo Lineal de dimensión 2), ) El grupo determinado por las matrices 2 x 2 invertibles.
- Para detalles sobre estos dos grupos, mirar en el capítulo Semigrupos, Monoides y Grupos.
- En tenemos que
- En el grupo de Klein [3] tenemos que cada elemento es su propio inverso.
- El neutro es único.
- Si e y e' son neutros entonces e * e'= e (ya que e' es neutro) y, también, e * e' = e' (ya que e es neutro). Luego, e' = e.
- Si, para algún a en G, se tiene que a * x = a (o que x * a = a) entonces x = e.
- Sea a' un inverso de a. Entonces,
- Análogamente para el otro caso.
- (Corolario). Si x * x = x entonces x = e.
- Esta aparentemente inocente propiedad puede servir para probar que un elemento de un grupo es el neutro.
- Cada elemento tiene un único inverso.
- Suponer que y, y' son inversos de x Entonces,
- Si a * x = e (o x * a = e) entonces x = a-1.
- a * x = e ==> a-1*(a * x) = a-1* e ==> (a-1 * a)* x = a-1 ==> x = a-1.
- Análogamente el otro caso.
- Luego, para mostrar que b es un inverso de a, basta con verificar que a * b = e (o que b*a = e).
- El inverso del inverso de un elemento, es el mismo elemento. (a-1)-1=a.
- Como a * a-1 = e, el resultado sigue de lo dicho arriba.
- El inverso de un producto es igual al producto de los inversos, pero con el orden invertido. (a*b)-1 = b-1*a-1.
- (a*b) * (b-1*a-1)=a*(b*b-1)*a-1 = a*a-1 = e, se tiene el resultado.
- (a) (Cancelación por la izquierda) a*b = a*c ==> b = c.
- (b) (Cancelación por la derecha) b*a = c * a ==> b = c.
- La ecuación a * x = b tiene solución única (x = a-1*b).
- La ecuación x * a = b tiene solución única (x = b * a-1).
- Análogamente el otro caso.
- Explicar de manera cuidadosa por qué los Racionales con la suma determinan un grupo y por qué los Racionales no nulos con la multiplicación determinan un grupo.
- Probar que en un grupo, un elemento que es inverso por la izquierda de otro elemento, también es inverso por la derecha de ese elemento. Es decir, que es un inverso del elemento. (Un elemento x'es inverso por la izquierda (resp. derecha) de x, ssi, x'* x = e (resp. x * x'= e).
- Resolver la ecuación en un grupo abeliano. ¿Cómo cambia la respuesta, si no suponemos conmutatividad?
- Sea G un grupo y Z(G) el subconjunto de G formado por todos aquellos elementos que conmutan con todos los elementos del grupo.
Probar que Z(G) es una parte cerrada de G que contiene al neutro y a los inversos de sus elementos. - Sea G un grupo y elementos del grupo. Probar que:
- Sea G un grupo y a un elemento de G. Sea (resp. ) la función de G en si mismo tal que (resp. ). Probar que (multiplicación por la izquierda de a) y (multiplicación por la derecha de a) son biyectivas. ¿Dónde en una tabla de operaciones de un grupo se puede ver los valores de (resp. de )?.
- Sea S un semigrupo donde las funciones y definidas como en el ejercicio anterior son biyectivas. Probar que es un grupo. ¿Es realmente necesario suponer que ambas funciones son biyectivas? (ver el próximo ejercicio.)
- Sea un semigrupo que tiene un neutro por la izquierda e inversos por la izquierda para todos sus elementos. Es decir que:
- hay un elemento tal que para todo en se cumple que y
- para cada de hay un tal que
Probar que es un grupo. (Sug. Probar primero que evaluando adecuadamente )
- Construir la tabla de la multiplicación de los enteros no nulos módulo 5 y módulo 6. Verificar que en el primer caso tenemos un grupo, pero no en el segundo caso.(Buscar los recíprocos de cada elemento).
- Sea G un grupo y sea a un elemento de G. Probar que el conjunto formado por todas las potencias naturales de a es una parte cerrada de G respecto a la operación.
- si entonces
- Demostración de (a): (Por inducción sobre n.) Sea m un natural cualquiera
- (n=0)
- Supongamos el resultado válido cuando Entonces,
- El resto se prueba de manera semejante.
- (a)
- (b)
- (c) si entonces
- (d)
- hay un entero positivo tal que Entonces, decimos que tiene orden finito que es igual al menor entero positivo con esa propiedad.
- para todo par de enteros positivos o cero, implica que Decimos que tiene orden infinito.
- En el grupo aditivo de los Enteros módulo 6, tenemos que (recordemos que potencias son los múltiplos)
- En el grupo de los Enteros, todos los elementos no nulos tienen orden infinito.
- En el grupo multiplicativo de los Complejos, el imaginario tiene orden 4.
- Los grupos cíclicos son grupos abelianos. (aras = ar+s = as+r = asar.)
- El inverso de ar es a-r. (ara-r = ar+(-r) = a0 =e.)
- Recordando la relación de Moivre que establece que tenemos que
Es decir que es una 12--ésima raíz de la unidad.
- Usando Moivre, tenemos que
- Cualquier potencia entera de \theta es también una raíz 12--ésima
- Hay solamente raíces diferentes de la unidad:
- Sean una raíz sexta de la unidad. Sean y Hallar los ordenes de .
- (Orden de un producto) Sean elementos de un grupo abeliano <G>. Si y probar que ¿Qué pasaría si no requiriéramos que operación fuera conmutativa?
- En las matrices siguientes, supondremos que las entradas están tomadas de Hallar el orden de cada una en el grupo lineal
- aba = a a2b = b.
- aababaab = aa(ba)baab = aaa2bbaab =a4b2aab =aaab = b.
4. Los grupos
[editar]Introducción
[editar]Los grupos representan, entre las estructuras algebraicas con una operación, aquellas con mayores propiedades algebraicas, ya que en un grupo la operación es asociativa, admite neutro y cada elemento es invertible respecto a la operación.
Dicha estructura aparecerá frecuentemente en todo nuestro trabajo posterior. Por esa razón, habrá varios capítulos dedicados al tema.
En los capítulos anteriores, los grupos fueron presentados conjuntamente con los semigrupos y monoides. Por comodidad para el lector, aquí revisaremos la mayoría de los temas referentes a grupos, aunque algunas veces referiremos al lector a los capítulos anteriores.

Definiciones y Ejemplos
[editar]Definición. (Grupo) Un Grupo es una estructura algebraica tal que:
Cuando no haya riego de confusión acerca de los parámetros [1] de la estructura, podemos hablar del grupo <G,*> o del grupo G con la operación * o, simplemente del grupo G.Nomenclatura.
Ejemplos de Grupos Numéricos
[editar]Empezaremos nuestros ejemplo con grupos de origen numérico.
Ejemplos de Grupos no conmutativos.
Ejemplos de Grupos definidos por Tablas
[editar]Podemos usar tablas de operaciones para visualizar o definir operaciones en conjuntos donde la cantidad de elementos es pequeña.
Ejemplo.
Consideremos el subconjunto de los complejos, donde i2 = -1. Veamos la tabla de multiplicación de ese conjunto.
Mirando a la tabla, vemos que 1 es un neutro y que cada elemento de U tiene recíproco (o sea inverso multiplicativo) en U. Como la multiplicación es asociativa, tenemos que efectivamente se trata de un grupo. La simetría respecto a la diagonal principal refleja que el grupo es abeliano.
Notemos que cada elemento de U aparece una sola vez en cada fila y en cada columna del interior de la tabla. Tales arreglos de símbolos se llaman cuadrados latinos. Las tablas anteriores se denominan tablas de Cayley (en honor a Arthur Cayley (1821-1895), quien las introdujo junto con una noción (abstracta) de grupo).
Grupos definidos por tablas.
Las tablas siguientes definen operaciones que proveen al conjunto subyacente con una estructura de grupo.
Un examen de las tablas muestra que las operaciones son conmutativas. En cada caso, mirando a la primera fila y primera columna, (fila y columna de encabezados o datos) vemos que es un neutro para la operación. En cada caso se puede buscar los inversos de cada elemento, ubicando al elemento en la columna de datos, luego nos movemos por la fila donde estaba ese elemento hasta ubicar el neutro. Subiendo hasta la fila de datos, hallamos el inverso.
Lo único que no se puede apreciar directamente de una tabla es si la operación es asociativa o no. Esto se deberá hacer por un examen exhaustivo de casos (bastante largo y aburrido) o por otro medio. Creyendo que las operaciones indicadas son asociativas (verificar unos tres casos) las tablas anteriores son tablas de grupos.
El grupo U, visto arriba, y el grupo de Klein son diferentes. La diferencia esencial no es que haya letras diferentes para los elementos, sino en sus propiedades algebraicas. Esto se puede apreciar porque la ecuación tiene dos soluciones en el primero (1*1 = 1 y (-1)*(-1)=1), mientras que tiene cuatro en el segundo. Sin embargo, mirando con cuidado, debería apreciarse que U y son esencialmente el mismo grupo. Esto implica, que a pesar del nombre de sus elementos los grupos y de Klein son diferentes grupos.
Moraleja: lo importante no es como se denotan o que son los elementos del conjunto del grupo, sino las propiedades de las operaciones del mismo.El grupo C2,a es representativo de todos los grupos con 2 elementos. Cualquier grupo con dos elementos tendrá un neutro, al que podemos llamar y un elemento diferente del neutro, que podemos llamar La primera columna y la primera fila de la tabla quedan determinada por las propiedades del neutro. Solamente nos falta ver que pasa con Hay solamente dos posibilidades Observemos que si multiplicando por el inverso de a en ambos lados obtendríamos que a = e, lo que es imposible. Luego, lo que nos dice que
Propiedades Básicas
[editar]En esta sección, G es un grupo con neutro e y para cada x, x' denota un inverso de x. Algunas propiedades son generales de operaciones, neutros e inversos, pero las repetiremos aquí, tanto por completitud como por lo que la estructura de grupo agrega.
Propiedades del Neutro
[editar]Recordemos que, por definición, e es un neutro de una operación * en un conjunto E, ssi, para todo a en E se cumple que a*e=a y e*a=a. En un grupo, veremos que basta que un elemento e cumpla con una de las ecuaciones anteriores para un solo elemento, para ser neutro.
Propiedades de los Inversos
[editar]Como hay un único inverso, podemos hablar de el inverso de x, al que denotaremos usualmente por
Por definición, un elemento y es un inverso de x, ssi, x * y = e y y * x = e. Veremos, que en un grupo, con solamente una de esas ecuaciones se tiene que y es el inverso de x.
Propiedades Cancelativas
[editar]Proposición 1. (Leyes de Cancelación) Sea G un grupo. Para todo a, b,c en G se cumple que:
Demostración: Basta en (a) premultiplicar por a-1 o en (b) posmultiplicar por a-1.
Ecuaciones en un grupo
[editar]Proposición 2. Sea un grupo. Para todo a, b en G se cumple que
Demostración:
Convenio. Para simplificar la escritura y la lectura, de ahora en adelante, a menos que se indique lo contrario, el producto se denotará como la multiplicación usual por "" o, como es costumbre, simplemente estará implícito entre los operandos.
Propiedades Heredadas
[editar]Sea un grupo. Si ignoramos o nos olvidamos del elemento neutro y de la existencia de inversos, obtenemos una estructura <G,*> de semigrupo, a la que llamamos el semigrupo subyacente del grupo G. Igualmente, si solo nos olvidamos de los inversos, obtenemos un monoide subyacente.
Como consecuencia de lo anterior, los grupos heredan todas las propiedades de los semigrupos, monoides y, por supuesto, de los magmas.
Ejercicios
[editar]
Potencias en un Grupo
[editar]Sea G un grupo con neutro e. Sea a un elemento de G. Para todo número natural n, la enésima potencia de a es, intuitivamente, el producto de a consigo mismo n veces. Formalmente, se define la potencia n--ésima recursivamente por:
Notemos que etc.
Proposición. (Propiedades de Potencias)
Sean a, b elementos del grupo y m, n naturales (o cero).
Podemos extender la definición de potencias para exponente nulo o negativo, agregando que
Es fácil verificar que las propiedades anteriores, también son válidas para exponentes negativos. Por ejemplo, si m es negativo y n positivo, se tiene que
Notación aditiva
[editar]Cuando la operación se escribe aditivamente, la operación de un elemento consigo mismo n veces, es un múltiplo del elemento.
Con esa notación, tenemos que las propiedades básica de los múltiplos enteros son:
Orden de un Elemento
[editar]El orden de un elemento de un monoide fue definido el capítulo Estructuras. Recordemos el orden finito de un elemento es el menor entero positivo tal que Aquí revisaremos la noción aplicada, principalmente, a elementos de un grupo. Sea un elemento de un monoide con neutro la definición de potencia con exponente natural hace sentido en un monoide, ya que no necesitamos de la existencia de inversos para probar las propiedades básicas. Consideremos la sucesión en
Cuando todos los elementos de la sucesión son diferentes entre sí, decimos que el orden de es infinito y escribimos
Supongamos, ahora, que en la sucesión apareciera un término que fuera igual a un término anterior. Digamos que con ¿Qué podemos concluir? Simplemente que a partir de el término --ésimo tendremos una porción de la sucesión que se repetirá indefinidamente. Por ejemplo con se tiene la sucesión
Por ejemplo, en con la mutgiplicación, tenemos que para las potencias naturales de 2, la sucesión (escribimos en lugar de ).
Recordemos que con la multiplicación no es un grupo. ¿Qué pasa cuándo estamos trabajando con un grupo y se tiene que ? Si multiplicando por el inverso de se tiene que o sea que Es decir, que tenemos un entero positivo tal que De acuerdo a la definición citada de orden, esto significa que tiene orden finito.
Proposición 3. (Orden de un elemento en un grupo ) Sea un grupo con neutro Entonces, para todo en se cumple que una, y solo una, de las alternativas siguientes:
Luego, en un grupo cada elemento o tiene orden finito o tiene orden infinito.
Corolario 3.1. Sea un grupo finito con orden Cada elemento de tiene orden finito y
-
Demostración: Consideremos la sucesión finita que tiene términos. Como solamente hay elementos en dos de esos términos deben coincidir. De donde sigue la finitud del orden de y la relación indicada.
Ejemplos.
Notemos que cuando entonces para cualquier múltiplo de digamos se cumple que La siguiente proposición, nos da un recíproco de ese resultado.
Proposición 4. Sea un elemento de un grupo Sea un entero positivo tal que Entonces el orden de es un divisor de
-
Demostración: Sea Por definición, es el menor entero positivo con esa propiedad. Dividiendo por , obtenemos un cociente y un residuo tales que
(*)
Entonces, Como , concluimos que . Es decir, por (*), que es un múltiplo de
Grupos Cíclicos
[editar]Definición. (Grupo Cíclico) Llamamos grupo cíclico a un grupo cuyos elementos son todos potencias enteras de uno de sus elementos. Dicho elemento se dice que es un generador del grupo.
Escribiremos , cuando G sea un grupo cíclico con generador a.Las potencias de un elemento de un grupo tienen las propiedades usuales de las potencias. Ver los ejercicios. En particular se tiene que
Notemos que cuando la notación es aditiva, en lugar de potencias tenemos múltiplos. Es decir, que en este caso un grupo es cíclico si todos su elementos son múltiplos de uno de ellos.
Ejemplo. (Los Enteros son un grupo cíclico.) Como para todo número entero m se cumple que vemos todos los enteros son múltiplos del número 1, Es decir que Los Enteros son un grupo cíclico con generador 1. Observemos que -1 también es un generador de por lo que un grupo cíclico puede tener más de un generador.
Ejemplo (Los Números Pares con la Suma).
Los números pares son los números enteros que son múltiplos de 2. Denotamos al conjunto de pares por Como la suma de números pares es un número par, la suma define una operación en el conjunto de los pares. La operación es asociativa, con neutro 0 (que es un número par). Cada número par, 2x, tiene como opuesto aditivo a 2(-x) que también es par. Este grupo es cíclico generado por 2,
Ejemplo. (Múltiplos de un número fijo).
Este ejemplo generaliza al ejemplo anterior. Consideremos el conjunto formado por todos los múltiplos enteros de un número entero fijo m.
. La suma de mx con my es igual a m(x+y), o sea un múltiplo de m. Tenemos que el neutro 0 (= m*0 ) es un múltiplo de m. El opuesto aditivo de mx es m(-x). Luego, es un grupo cíclico con generador m.
Como este grupo es un grupo respecto a las mismas operaciones del grupo se dice que es un subgrupo de los Enteros con la suma.
Ejemplo (Raíces n-ésimas de la unidad).
Llamamos raíz n-ésima de la unidad a cualquier número complejo tal que Consideremos el caso y sea
Sea un entero cualquiera, la división por , nos produce y tales que , con
Luego Lo que prueba que hay raíces de la unidad:
Simbolizaremos por al conjunto formado por todas las raíces enésimas de la unidad. es un grupo cíclico con elementos.
Observemos que es nuestro viejo conocido
(Existencia de Grupos Cíclicos). El ejemplo de las raíces de la unidad muestra que para todo número entero positivo , hay un grupo cíclico con exactamente elementos,
Ejercicios
[editar]Grupos definidos por Generadores
[editar]Un grupo puede definirse mediante generadores sujeto a restricciones (relaciones entre los generadores), lo que se representa como
que leemos como que "G es el grupo generado por a,b,c, que satisfacen las restricciones r_1(a,b,...), r_2 (a,b,.. ) ..."
Formalmente, lo anterior significa que el conjunto G consiste de productos formales de expresiones formadas por potencias de los generadores.
Podemos considerar a los generadores como las letras de un alfabeto. Poniendo esas letras juntas formamos palabras. Una potencia de una letra significa que la letra está repetida tantas veces como el exponente. Cuando el exponente es nulo, se considera que es la palabra vacía (sin letras). La operación es la concatenación de palabras, esto es pegarlas juntas, que es claramente asociativa y tiene como neutro a la palabra vacía (sin letras). El largo de una palabra es la cantidad de letras de la palabra. En los lenguajes de programación, se denomina cadenas a la concatenación de letras (llamadas caracteres en ese contexto).Ejemplo (Grupo Cíclico Finito).
Sea donde n es un natural positivo. Los elementos de Cn,a son palabras consistentes solamente de aes, es decir potencias de a. Por lo que se trata de un grupo cíclico. La restricción consiste en que consideramos que cuando haya n de esas letras, la palabra será (por la restricción) considerada como igual a la palabra vacía. (Podemos decir que si hay n letras aes juntas, las podemos borrar.) Suponemos, además, que el número n es el menor entero positivo con esa propiedad. Lo que implica, de acuerdo a lo visto en el ejemplo de las raíces enésimas de la unidad, que
Esencialmente, hay un único grupo cíclico de orden n; la única diferencia entre ellos es como simbolizamos la operación y al generador. Cuando el nombre del generador no sea importante, simplemente escribiremos para el grupo cíclico de orden . Mayores detalles para los grupos cíclicos, los veremos en el capítulo [4].
Ejemplo (Grupos Diedrales).
Llamamos grupo diedral de orden 2n, al grupo denotado por y definido como
Notemos que los elementos de son productos de expresiones de la forma con La tercera restricción nos dice que el grupo no es conmutativo, pero indica que podemos rearreglar las letras de modo que las aes estén delante de las bes.
Supongamos, para concretizar, que n = 3. Entonces. implica que ba = a2b. Por lo que
Lueego, los elementos de son los productos de la forma con Es decir que
o sea que tiene 2n elementos. Además, como
Cada elementos es invertible. Es decir que es un grupo.Los grupos diedrales provienen de las simetrías de un polígono regular de lados. (Congruencias que dejan fijo globalmente al polígono). Mayores detalles en el capítulo sobre Grupos Generados.
Ejercicios
[editar]- Verificar que las definición de potencia natural y sus propiedades son válidas para cualquier monoide; y que si tomamos a1=a como punto de partida de la definición de potencias (en lugar de a0), las propiedades son válidas para cualquier semigrupo.
- Construir las tablas de para n = 2, 3, 4, 5. En cada caso identificar los inversos de los elementos.
- Sea G = C12,a = <a | a12=e>. Probar que G tiene elementos de orden 2, 3, 4 y 6, pero no tiene elemento de orden 5.
- Probar las relaciones no probadas de potencias, especialmente con exponentes negativos.
- Probar que cuando a conmuta (o permuta) con b (ab=ba) se cumple que:
- a conmuta con cualquier potencia natural de b,
- a conmuta con el inverso de b.
- el inverso de a conmuta con cualquier potencia entera de b.
- Sea . no Probar que G es el grupo de Klein.
- Hallar los ordenes de todos los elementos del grupo diedral .
- Verifica que cuando la operación no es conmutativa, en general no se cumple que
- Sea Probar que G es un grupo infinito no abeliano con elementos de orden infinito, cuando
Producto de Grupos
[editar]Sean <H ,*> y <K, #> grupos. Sea el producto cartesiano de los conjuntos H y K, es decir el conjunto formado por todos los pares ordenados (x,y) tales que x están H, y está en K. Definimos una operación en G, coordenada a coordenada,
Proposición. (Grupo Producto)
Sean H, K y G como arriba. Entonces G es un grupo.Demostración: Tenemos que
Lo que prueba la asociatividad.
Sean eH y eK los neutros de H y K respectivamente. Sea e = (eH, eK). Entonces, De forma similar se prueba que Por lo que e es neutro respecto a la operación.
Finalmente, Análogamente,
Definición. (Producto de Grupos) Llamamos producto de los grupos H y K al grupo provisto de la operación por coordenadas.
Cuando la notación es aditiva, podemos llamar suma al producto. El grupo aditivo .
Consideremos al grupo aditivo de los Reales. es el producto cartesiano de los Reales consigo mismo. es un grupo abeliano con operación
(Esta es la suma usual de vectores de dimensión 2 o la suma de los complejos.)
En general, cuando se toma el producto de un grupo G consigo mismo, el producto se denota por G2. Si se toma el producto de un grupo G consigo mismo n veces, denotamos al producto resultante por Gn; sus elementos son n--uplas de elementos de G.
Ejercicios
[editar]- Probar que si H y K son abelianos, entonces también lo es H x K.
- Construir la tabla de C2,a x C2,b. Compara la tabla que se obtiene con la tabla del grupo de Klein.
- Sean C3,a y C4,b grupos cíclicos de orden 3 y 4, con generadores a y b, respectivamente. Probar que el producto C3,a x C4.b es cíclico con generador (a,b).
- Sean C4,a y C2,b grupos cíclicos con generadores a y b respectivamente. Probar que el producto C4,a x C2,b no es cíclico.
- Construir las tablas de
Ejercicios del Capítulo
[editar]- Sea G un grupo finito. Probar que para cada a en G hay un entero positivo n tal que
- En un grupo G, para elementos g y x definir (Conjugado de x por g). Probar que se cumplen las siguientes relaciones.
- xg y g = (xy)g.
- (xg)-1 = (x-1)g.
- (xg)n = (xn)g.
- Hallar el orden de todos los elementos del grupo simétrico S3. Ver la definición en el capítulo Las Estructuras.
- (Grupos de Transformaciones) Sea X un conjunto no vacío. Un grupo de transformaciones de X es un grupo G tal que sus elementos son elementos del grupo (Funciones biyectivas de X" en si mismo).
- Sea x en X y sea el conjunto formado por todas las transformaciones f de G que fijan el punto x, es decir que f(x) = x. Probar que es cerrado respecto a la composición, contiene a la identidad y a los inversos de cada uno de sus elementos, es decir, que se trata de un grupo de transformaciones. Por ejemplo, en el grupo de las congruencias del plano, las rotaciones entorno al origen, son precisamente las congruencias que dejan fijo únicamente al origen.
- Dado un subconjunto de X, el conjunto denota a las biyecciones de G que dejan fijo globalmente a Y, Es decir, Probar que es un grupo de transformaciones. En el grupo de las congruencias, la simetría que voltea el plano alrededor del eje X, deja al eje Y fijo globalmente, aunque todos sus puntos, exceptuando al origen, se mueven a un punto distinto. Esta misma simetría deja fijo al eje de X puntualmente, o sea punto a punto.
- Sea (el grupo multiplicativo de los invertibles en ). Probar que Concluir que no es un grupo cíclico.
- Considerar el grupo Probar que el orden de G es igual a 8 y que, aunque 4 divide a 8 no hay elemento de orden 4 en G. Concluir de lo anterior que G no puede ser cíclico.
- Sea G = <a> un grupo cíclico de orden impar. Probar que a aparece en la diagonal principal de la tabla del grupo.
- Probar que el grupo multiplicativo no es cíclico.
- Sea el conjunto formado por todas los complejos cuyo módulo es igual a 1. Probar que es cerrado respecto a la multiplicación, contiene al 1, y a los inversos de cada uno de sus elementos. Por lo que tiene una estructura de grupo. Mostrar que dicho grupo contiene elementos de orden finito de cualquier orden. (Sug: Considerar las raíces n--ésimas de la unidad.)
- Sea Probar que G es finito y cíclico.
- ¿Por qué podemos estar seguro que los grupos diedrales no son cíclicos?
- Determinar cuáles de los siguientes conjuntos de matrices, respecto a la operación indicada determinan un grupo. Recordar que una matriz diagonal es una matriz cuadrada cuyas únicas entradas no nulas están en la diagonal principal. Una matriz es triangular superior, cuando las entradas debajo de la diagonal principal son nulas. El determinante de una matriz es un número asociado a cada matriz cuadrada y es tal que
- donde ( es la matriz identidad, una matriz diagonal con todas la entradas en la diagonal iguales a 1), y
- una matriz es invertible, ssi, su determinante es diferente de cero.
- Las matrices diagonales con la suma de matrices.
- Las matrices diagonales con la ~multiplicación de matrices.
- Las matrices diagonales cuyas entradas son todas 1 o con la multiplicación'on.
- Las matrices triangulares superiores con la suma.
- Las matrices triangulares superiores con la multiplicación.
- Las matrices con determinante positivo con la multiplicación.
- Las matrices cuyo determinante es 1 o con la multiplicación.
- Sea el grupo de las matrices invertibles. Sea el subconjunto de G formado por todas las matrices cuyo determinante es positivo. Probar que es cerrado respecto a la multiplicación de matrices (usar una famosa identidad de determinantes), contiene a la matriz identidad y a los inversos de cada uno de sus elementos. Es decir que se trata de un grupo de transformaciones..
- Sea G un grupo y H un conjunto finito de G que es cerrado respecto a la operación. Probar que H es con la misma operación es un grupo.
- Sea el conjunto formado por todos los números reales excepto Definir * en por
- Probar que es un grupo. .
- Hallar la solución o soluciones de la ecuación f the equation en
- Sea un grupo finito. Probar que cada elemento de tiene orden finito.
(Considerar donde ), - Sea T el conjunto de números reales no nulos. Definir
- Muestre que * es asociativa.
- Probar que * tiene neutro por la izquierda e inversos por la derecha
- ¿Es un grupo?
- Sea tal que para todo se cumple que Probar que es abeliano. (Sugerencia: considerar )
- Probar que si, en un grupo< se cumple que entonces,
- Sea un grupo y suponga que Pruebe que también
- Sea
Probar las siguientes afirmaciones.
- Todos los elementos de son de la forma y Concluir que el orden de es 8.
- El orden es 2, para cualquier valor de
- Determinar todos los subgrupos de Indicar cuántos de ellos son cíclicos.
- Sea un grupo de orden par. Probar que si un elemento de aparece en la diagonal principal de la tabla, lo hace una cantidad par de veces.
- Sea un grupo de orden con impar. Probar que tiene exactamente un elemento de orden 2, Además que el producto de todos los elementos del grupo es precisamente ese elemento de orden 2.
Comentarios
[editar]La noción de grupo aparece en matemáticas por tres caminos, aparentemente independientes: la búsqueda de una fórmula para resolver la ecuación de quinto grado, las aritméticas modulares y la geometría.
Resolución de ecuaciones. Los matemáticos de fines del siglo XVIII e inicios del siglo XIX (Lagrange, Ruffini, Cauchy, Abel, Galois) se preocuparon de expresiones algebraicas relacionando las raíces de las ecuaciones y que permanecían invariantes (no cambiaban de valor) cuando se permutaban dichas raíces. Los trabajos de Abel y las geniales construcciones de Galois [5], asociando grupos a ecuaciones, trajeron los grupos a primer plano. Todo el tiempo, esos grupos eran grupos de permutaciones. Alrededor de la mitad del siglo XIX, Arthur Cayley formuló una definición abstracta de grupo, semejante a la usada actualmente.
Aritmética modular. Los enteros módulo un entero positivo hacen sus primeras apariciones con Euler. Su estudio fue continuado por Gauss que analizo ejemplos muy generales de lo que llamaríamos hoy día grupos abelianos.Geometría Desde los inicios del siglo XIX, los estudios de geometrías proyectivas y no--euclidianas condujo al estudio de las propiedades e invariancia de propiedades con respecto a ciertas transformaciones (preservación de colinealidad, paralelismo, etc.) Tales estudios hicieron aparecer de forma natural grupos en la Geometría. A finales del siglo, Felix Klein definiría a la Geometría como el estudio de los invariantes de un grupo, Erlargen Programm, 1872.
Otras fuentes. Paralelo al desarrollo de los grupos finitos, que expresaban de forma natural las clasificaciones de las simetrías de estructuras cristalinas (usadas hasta hoy por los químicos), se desarrolló el estudio de grupos infinitos, especialmente grupos de matrices. La teoría de esos grupos ayudó, y también se impulsó, por las aplicaciones a las teorías físicas del siglo XX (relatividad, mecánica cuántica, partículas elementales).
Las siguientes páginas de Wikipedia pueden agregar más información acerca de la teoría de grupos y sus aplicaciones.- Grupos (matemática)
- Teoría de Grupos
- Teoría geométrica de grupos
Notas
[editar]5. Los Homomorfismos de Grupos
[editar]Introducción
[editar]Hemos visto en el capítulo anterior tres grupos de orden 4: C4,a, el grupo de Klein y el grupo de las raíces cuartas de la unidad, U4 = U4(). ¿Son esos grupos distintos? La respuesta sería aparentemente afirmativa, si nos fijáramos solamente en sus elementos. Sin embargo, en Álgebra Abstracta estamos más interesados en las propiedades de las operaciones que de la manera como simbolizamos a los elementos. Observemos que tanto C4,a como U4 son grupos cíclicos con generadores a e i respectivamente y que tenemos el siguiente pareo.
El pareo hace que el algebra de ambos grupos luzca bastante similar. La manera de comparar dos grupos será la noción de homomorfismo, la cual formalizará la noción de semejanza de dos grupos.
En este capítulo, veremos como usar funciones especiales (isomorfismos) entre grupos para realizar comparaciones que nos permitan detectar o verificar isomorfías (iguales formascomo las indicadas arriba. De forma más general, estudiaremos homomorfismos que serán funciones que preservan los parámetros de la estructura de grupo.
Definiciones
[editar]Definición. (Homomorfismo de Grupos) Sean y grupos.
Un homomorfismo del grupo G en el grupo G' es una función tal que- permuta con las operaciones:
- envía neutro en neutro:
- envía inversos en inversos:
Tipos de Homomorfismos
Un homomorfismo es un:- monomorfismo, cuando es inyectiva.
- supramorfismo, cuando es suprayectiva.
- isomorfismo, uando es biyectiva.
- endomorfismo, cuando es un homomorfismo de en sí mismo.
- automorfismo, cuando es un isomorfismo de en sí mismo.
Cuando haya un isomorfismo de un grupo G en un grupo G', decimos que los grupos son isomorfos y escribimos .
Decimos que un grupo H es una imagen homomórfica de un grupo G, cuando haya un supramorfismo de G en H.
Ejemplo Clásico de Homomorfismo.
El prototipo de homomorfismo (de hecho es un isomorfismo) es el logaritmo que transporta la estructura multiplicativa de los Reales positivos en la estructura aditiva de los Reales. ya que
- ,
- , y
- .
función biyectiva, ya que tiene a la función exponencial como inversa.
Ejemplo. (Homomorfismo trivial).
Sean G y H grupos cualesquiera. La función que asigna a cada x de G el elemento neutro de H es un homomorfismo que llamaremos el homomorfismo trivial
Ejemplo. (Los grupos U4 y C4 son isomorfos).
Sea f la función que envía en . Como todos los elementos de ambos grupos son potencias de sus generadores
tenemos queClaramente, f es biyectiva, por lo que los grupos son isomorfos.
Endomorfismo aditivo de .
Sea tal que Es fácil ver que se trata de un endomorfismo de grupos, ya que
Luego, tenemos un endomorfismo (porque va de un grupo en sí mismo) que es inyectivo, pero no suprayectivo.
Propiedades de los Homomorfismos
[editar]La definición dada de homomorfismo arriba, es la definición general de homomorfismo de estructuras[6]. En el caso de los homomorfismos de grupos, tenemos que la primera condición implica a las otras dos.
Proposición 1. (Caracterización de Homomorfismos de Grupoa). Sean y grupos. Una función
es un homomorfismo, ssi, para todo x, y de G se cumple que
-
Demostración: La condición es claramente necesaria. Veamos
que es suficiente. Observemos que ,
lo que implica que Por su parte ; de donde :Lo
que prueba la proposición.
Ejemplo.
La función que asocia a cada entero su clase de congruencia módulo m es un supramorfismo, ya que es suprayectiva y
Ejemplo (Determinante de Matrices).
La función determinante (de matrices) tiene la siguiente propiedad
Por lo que define un homomorfismo del grupo de matrices invertibles GL2 en el grupo multiplicativo de los Reales. Por la proposición, tenemos que el determinante de la matriz identidad es 1 y el determinante de la inversa de una matriz es el recíproco del determinante de la matriz.
Ejemplo (Grupo Producto).
Sean G, H, K grupos tales que . Sea tal que (proyección en la primera coordenada). es un supramorfismo, ya que
Resultado análogo para la segunda proyección.
Proposición 2. (Composición de Homomorfismos) La composición de dos homomorfismos es un homomorfismo.
-
Demostración: Sean y homomorfismos. Entonces.
Sea un homomorfismo de grupos y sea x un elemento de . Probaremos que para todo natural, . Si , . Suponiendo el resultado para valores menores de n, tenemos
Proposición 3. (Homomorfismos y Potencias) Sea un homomorfismo de grupos y sea x un elemento de G. Entonces, para todo entero n se cumple que
-
Demostración: La discusión previa al enunciado prueba el resultado para valores no negativos de n. Sea n > 0, entonces
Corolario 3.1. Sea un homomorfismo de grupos y sea x un elemento de G. Entonces, el orden de f(x) divide al orden de x.
-
Demostración: Sea n=o(x). Entonces, xn = e ,
lo que implica que . Por lo que n es
un múltiplo de o(f(x)).
Ejercicios
[editar]- ¿Cuáles de las funciones siguientes son homomorfismos de grupos?
es el grupo aditivo de los Reales y el
grupo multiplicativo de los Reales no nulos.
- .
- .
- .
- .
- .
- Sea . Sea tal que . Probar que es un monomorfismo de grupos. Definir un y enunciar y probar un resultado análogo.
Isomorfismos de Grupos
[editar]Recordemos que un isomorfismo de grupos es un homomorfismo biyectivo y que significa que los grupos son isomorfos, es decir que hay un isomorfismo de G en G'. Notemos que la relación de isomorfismo entre grupos es reflexiva, simétrica y transitiva.
- Si un isomorfismo y es la inversa de f como función tenemos que
para todo x' = f(x), y' = f(y) que g(x'y') = g(f(x)f(y)) = g(f(xy))= xy = g(x') g(y'). Es decir que la función inversa de un isomorfismo es también un isomorfismo. - Si tenemos isomorfismos y , entonces su composición es un homomorfismo biyectivo, por lo que es un isomorfismo.
Al pasar, hemos probado la siguiente proposición.
Proposición 4. (Propiedades de Isomorfismos)
- La función inversa de un isomorfismo es un isomorfismo.
- La composición de isomorfismos es un isomorfismo.
Observaciones. El logaritmo fue el primer ejemplo conocido de un isomorfismo de grupos. Permite transportar problemas de una estructura en la otra. Multiplicar es más difícil que sumar, por lo que para multiplicar dos números, sumamos sus logaritmos y, luego, usando, la inversa (que es la exponencial) obtenemos el resultado de la multiplicación.
Esto podrá parecer muy complicado al lector acostumbrado a las calculadoras electrónicas, pero cuando estas no existían, los cómputos de productos se realizaban obteniendo valores de logaritmos y de antilogaritmos (la función inversa) desde libros con tablas de valores de dichas funciones.
La Clasificación de Grupos El objetivo central de la teoría de grupos es la clasificación de los mismos. Esto es determinar todos los posibles tipos de grupos no isomorfos entre si.
Desde el punto de vista de la teoría de grupos, dos grupos isomorfos son esencialmente el mismo grupo, la única diferencia reside en el nombre usado para los elementos del grupo, como lo discutido al inicio del capítulo. Por lo que, a veces, diremos que grupos con una cierta propiedad son únicos, significando que cualquier par de grupos con la propiedad son isomorfos. Esto significa que para probar que dos grupos no son isomorfos basta con verificar que hay una propiedad de uno de ellos que no tiene el otro.
Por ejemplo, grupos con un solo elemento son todos isomorfos entre si, por lo que decimos que hay un único grupo con un elemento.
Clasificación de los grupos de orden 2.
Hay un único grupo de orden 2, excepto por isomorfismos.
Vimos este resultado, anteriormente, analizando las posibilidades para el producto del elemento diferente del neutro. Aquí, veremos el mismo resultado pero usando isomorfismos. Sean G={e,a} y H = {e',a'} donde los elementos neutros son e y e' respectivamente. Sea g la función de G en H tal que g(e)=e' y g(a) = a'. Entonces,
Lo que prueba que g es un isomorfismo.
Los isomorfismos preservan la estructura interna de un grupo. En particular, preservan ordenes de elementos. En efecto, sean un isomorfismo y x un elemento de G, entonces tenemos, por un corolario anterior, que . como y es un homomorfismo, tenemos que . de donde, la igualdad. Aplicaremos esta observación más adelante.
Dos grupos de orden 4 que no son isomorfos.
Los grupos cíclicos de orden 4, C4 y K (grupo de Klein), vistos a propósito de las tablas de grupo en el capítulo anterior, no son isomorfos. En efecto, en C4 hay, por definición de grupo cíclico un elemento de orden 4, mientas que en el grupo de Klein todos los elementos diferentes del neutro tienen orden 2. Por lo tanto, los grupos no pueden ser isomorfos.
Isomorfismo de Grupos Cíclicos
[editar]Nuestra próxima proposición formaliza algo que podíamos haber intuido.
Proposición 5. (Isomorfismo de Cíclicos) Dos grupos cíclicos de igual orden son isomorfos.
-
Demostración: Sean G=C_n,a y H =
C_n,b. Definamos f:G en H por f(ak) =
bk. Se tiene entonces que
Lo que prueba que f es un homomorfismo. Además, claramente, f es suprayectiva. Supongamos que . Sin perdida de generalidad, podemos suponer que , por lo que tenemos que $0 \le j \le k <n$. Se tiene que . Si , sería un número positivo menor que . Lo que es imposible, ya que porque por las hipótesis es el menor entero positivo con la propiedad de que . Luego , o sea que es inyectiva. Lo que concluye la
prueba.
Isomorfismo de Grupos Simétricos
[editar]Recordemos que el grupo simétrico, , es el grupo formado por todas las biyecciones del conjunto en sí mismo. Probaremos que cuando dos conjuntos tienen igual cantidad de elementos, sus grupos simétricos son isomorfos. por lo que el grupo simétrico dependerá solamente de la cardinalidad del conjunto, pero no necesariamente del conjunto específico.
Recordemos que dos conjuntos tienen igual cantidad de elementos (o igual cardinal) cuando, y solo cuando, hay una biyección de un en el otro. Sean X, Y conjuntos con el mismo cardinal y sea la función biyectiva que establece la igualdad de cardinales. Definamos tal que para todo en , asociamos la función de Y en sí mismo.

Como es una composición de biyecciones, se trata de una biyección de Y en Y, o sea de un elemento de . Veamos, ahora, que es un
homomorfismo.Claramente, la asignación para cada de de de es una función inversa de por lo que es una biyección, lo que prueba que se trata de un isomorfismo de grupos.
Proposición 6. (Isomorfismo de Grupos Simétricos) Cuando y son conjuntos con igual cantidad de elementos, sus grupos simétricos son congruentes. .
Corolario 6.1. El grupo simétrico de cualquier conjunto con elementos es isomorfo a el grupo simétrico de .
El Grupo de Automorfismos de un Grupo
[editar]Recordemos que un automorfismo de un grupo es un isomorfismo del grupo en sí mismo.
Sea G un grupo, por Aut(G) denotaremos al conjunto formado por todos los automorfismos del grupo. Como la composición de automorfismo es un automorfismo, lo mismo que la identidad y el inverso de un automorfismo, tenemos que Aut(G) con la composición de funciones forman un grupo, contenido en .
Automorfismos de .
Sea un automorfismo de grupos. Entonces como es un generador del grupo, su imagen <math<f(a)</math>debe ser un generador del grupo.
-
(n=5) Es fácil ver por inspección, que los generadores de son para . Luego, hay cuatro automorfismos, definidos tales que para . Observemos
que implica que ,
es decir que , la función identidad, y, por lo tanto, el neutro
del grupo de automorfismos. Por simple computación, obtenemos la siguiente
tabla para
Lo que prueba que - (n=6) En hay solo dos generadores, y <math?a^5</math>.. Por lo que hay solamente dos automorfismos: y . Por lo que
Ejercicios del Capítulo
[editar]- Sea P el subconjunto de formado por todos los enteros pares. Probar que la función es un homomorfismo de grupos desde en P ¿Es un isomorfismo?
- Sea un homomorfismo de grupos.
Probar las siguientes afirmaciones.
- Para todo a de G y n entero se cumple que .
- Para todo a, b en G, si a conmuta con b en G, lo mismo pasa con sus imágenes en H.
- Si a es conjugado con b en G, entonces f(a) es conjugado con f(b) en H.
- Si hay un a en G tal que an=e para algún n natural, hay un elemento de H con la misma propiedad.
- Sea una imagen homomórfica de . Probar
las afirmaciones siguientes.
- Si G es abeliano, H también lo es.
- Si G es cíclico, H también lo es.
- Sea un isomorfismo. Probar que para cada n natural, la cantidad de elementos que satisfacen la ecuación en G, es la misma que los elementos que satisfacen la ecuación en H.
- Sea un isomorfismo. Probar que la inversa de , es un isomorfismo.
- Probar las siguientes afirmaciones.
- La composición de monomorfismos es un monomorfismo.
- La composición de supramorfismos es un supramorfismo.
- La composición de isomorfismos es un isomorfismo.
- ¿Pueden haber dos grupos finitos con diferente orden que sean isomorfos?
- Sea (pares ordenados de números racionales que no tienen ambas componentes nulas). Definamos, una nueva operación en G por Sea f la función de G en el grupo multiplicativo de los complejos, tal que , donde . Probar que G es un grupo abeliano y que f es un monomorfismo de grupos.
- Sean un producto de grupos . Sean y tales que pr1(h,k) = h y pr2(h,k) = k. Probar que las proyecciones pr1 y pr2 son supramorfismos.
- Sean y homomorfismos de grupos. Sea tal que . Probar que es un homomorfismo de grupos.
- Sean G, H y K grupos. Probar que
- .
- .
- , donde es el grupo trivial con un elemento.
- Sea <G,*> un grupo. Probar que la operación (considerada como función) de en G es un homomorfismo de grupos, ssi, G es abeliano.
- Probar que es isomorfo al grupo de Klein (comparar las tablas de operaciones), por lo que no puede ser isomorfo a .
- Probar que dos grupos con tres elementos son siempre isomorfos.
- (Endomorfismos del grupo aditivo de los Racionales) \quad
- Sea tal que f(q) = aq, donde a es un número racional fijo. Probar que f es un endomorfismo del grupo aditivo de los racionales, que es un automorfismo cuando .
- Sea un endomorfismo del grupo aditivo de los Raciones. Probar que , donde .
- Sea G un grupo de orden par. Probar que siempre G contiene un elemento de orden 2.
- Hallar los homomorfismos de en sí mismo. ¿Cuántos de ellos son isomorfismos?
- Hallar, si existe, un homomorfismo no trivial entre los grupos. indicados. Si no
existe, explicar por qué no existe.
a. . b. c. . d. . e. . f. . g. .
h. i. . j. . - (Homomorfismos de Semigrupos y Monoides) Definir homomorfismos para semigrupos y monoides.
Notas
[editar]- ↑ Llamamos parámetros de una estructura a todos los componentes diferentes del conjunto base.
- ↑ En honor a N. H. Abel (1802-1829)
- ↑ Felix Klein (1802)
- ↑ Los grupos cíclicos
- ↑ Louis Evariste Galois (1811-1832)
- ↑ Véase el apéndice La teoría de las Estructuras Algebraicas.
6. Los subgrupos
[editar]Introducción
[editar]En un capítulo anterior, vimos grupos que vivían dentro de otro grupo. El grupo de los múltiplos de un número entero está contenido en el grupo de los Enteros. El grupo de las raíces --ésimas de la unidad está contenido en el grupo multiplicativo de los Complejos.
Algunas veces se dice, de manera muy simple, que un subgrupo es un grupo que vive dentro de otra estructura. Como todas la cosas simples, hay algo de verdad en lo anterior; pero debe manejarse con cuidado. Por ejemplo el conjunto es un subconjunto de los Enteros que es un grupo respecto a la multiplicación, está contenido en los Enteros, pero no está relacionado con el grupo aditivo de los Enteros porque se trata de operaciones distintas.
En forma general, cuando tenemos una estructura algebraica, un subconjunto del conjunto base de la estructura define una subestructura del mismo tipo cuando es cerrado respecto a los parámetros [1] de la estructura.
Definiciones
[editar]Definición. (Subgrupo) Sea <G,*,e, x -->x-1>un grupo. Un subconjunto no vacío H de G determina (o define) un subgrupo de G, ssi,
- (i)(Cerrado respecto a la operación.)
- Para todo a, b en G, a,b en H ==> ab en H.
- (ii) (Cerrado respecto al neutro).
- El neutro es un elemento de H.
- (iii)(Cerrado respecto inversos.)
- Para todo a en G, a en H ==> a-1 en H.
- Para todo a en G, a en H ==> a-1 en H.
- Notación: H < G.
La definición corresponde a la definición general de subestructura [2]. La riqueza de la estructura de grupo nos permite, sin embargo, reducir las condiciones.
Proposición 1. (Caracterización de Subgrupos)
Un subconjunto no vacío H de G define un subgrupo de G, ssi, para todo a, b en G se cumple que a, b en H implica que también está en H. </math>-
Demostración:
- Claramente las condiciones son necesarias. Si y están en , está en (parte (iii) de la definición). Luego está en (parte (i) de la definición).
- está en ,
- está en .
- está en .
Ejemplos de Subgrupos
[editar]Cada grupo es siempre un subgrupo de sí mismo. Igualmente, es un subgrupo de cualquier grupo. Algunas veces, diremos que el subgrupo determinado por el elemento neutro es el subgrupo nulo o subgrupo trivial. Decimos que un subgrupo es propio cuando es diferente de y del subgrupo trivial.
Subgrupos Aditivos de los Enteros
[editar]Sea m un entero y sea H= mZ</math> el conjunto formado por todos los múltiplos enteros de .
Claramente, H no es vacío. Sean a = mx, b = nx y múltiplos enteros de m. Entonces, a-b = mx - my = m(x-y). Lo que prueba que a-b es un múltiplo de m. Luego mZ es un subgrupo de los Enteros.
- Los únicos subgrupos de los Enteros son los mZ.
Sea H un subgrupo de los Enteros. Si entonces . Supongamos que H contiene un elemento no nulo, digamos c. Como c en H implica (-c) en H, sin perdida de generalidad, podemos suponer que c es positivo. Sea m el menor entero positivo contenido en H y sea z cualquier elemento de H. Por división por m, tenemos que
Como H es un grupo y z y m están en H, tenemos que también están en H, qm y z. Por lo que r=z-qm también está en H. Si r fuera positivo sería menor que el menor entero positivo en H, lo que es imposible, luego, r=0. En consecuencia, z es un múltiplo de m. Lo que prueba la afirmación.
Subgrupos Cíclicos
[editar]Proposición 2. (Subgrupo Cíclico) Sea G un grupo y a un elemento de G. Sea . Entonces, H es un subgrupo de G, llamado subgrupo cíclico de G generado por a y denotado por
-
Demostración: H es claramente no vacío, ya que contiene a Además, tenemos que Lo que prueba que H < G.
- Los subgrupos de los Enteros son subgrupos cíclicos.
- El orden del subgrupo es igual al orden de , .
Subgrupos del Grupo Simétrico S3
[editar]Sea .
La relación "ba = a2b" nos dice que la operación no es conmutativa, por lo que S3 no puede ser un grupo cíclico. Sigue directo de la definición que o(a)=3 y o(b) = 2. Como (ab)2 = abab = aa2bb = e y (a2b)2 = a2ba2b =a2abb = e, tenemos que o(ab) = o(a2b)=2. Por su parte, si x = a2, x2 = a y x3 = e, luego o(a2)=3. Tenemos, entonces los siguientes subgrupos cíclicos:
No hay otros subgrupos aparte de {e} y S3.
En efecto, sea H un grupo que contiene a . Entonces, el subgrupo generado por a contiene todas las potencias de a. Si contiene algún elemento adicional debe ser de la forma , que multiplicado por a3-i produce b. Como H contiene a los dos generadores del grupo, debe ser igual a todo el grupo.
Razonando de igual manera, con otras posibilidades, se concluye que los únicos subgrupos posibles, son los subgrupos indicados arriba.
Diagramas de Subgrupos
[editar]El diagrama de subgrupos es la presentación gráfica de las relaciones de inclusión entre un grupo y sus subgrupos. También se llama en la literatura, diagrama de Hasse. La figura siguiente ilustra el diagrama de subgrupos del grupo de Klein y del grupo simétrico. S3
Grupo de Klein Grupo Simétrico S3 

Ejercicios
[editar]- Hallar todos los subgrupos posibles de los grupos C4 y C6. Dibujar los diagrams de subgrupos de esos grupos.
- Sea U() el subconjunto formado por todos los complejos cuyo módulo es igual a 1. (Si z = a + bi, su modulo es ).
Un( es el grupo de la raíces {i}n{/i}-ésimas de la unidad.
- Probar que U() es un subgrupo multiplicativo de los Complejos.
- Probar que para todo n, Un() es un subgrupo de U().
- Probar que U2() = es un subgrupo de U4().
- Probar que U3() es un subgrupo de U6().
- ¿Cómo podríamos generalizar los resultados anteriores?
- Sea G un grupo y a un elemento de G. Sea H el conjunto formado por todos los g en G que permutan (respecto a la operación) con a, o sea tales que ga = ag. Probar que H es un subgrupo de G.
- Sea G un grupo finito. Sean a y b elementos de G. Probar las siguientes relaciones acerca de sus ordenes.
- .
- .
- Si entonces .
- Si y entonces .
- ¿Cuáles de los conjuntos siguientes determinan subgrupos aditivos de los Complejos?
- Los Enteros.
- Los Racionales de la forma , , y enteros.
- Los números puramente imaginarios. (múltiplos de ).
- ¿Cuáles de los conjuntos siguientes determinan subgrupos multiplicativos de los Complejos no nulos?
- Los Enteros no nulos.
- Los Racionales de la forma , , , y enteros.
- Los números puramente imaginarios y no nulos. (múltiplos de ).
- ¿Cuáles de los conjuntos de matrices son subgrupo del grupo lineal, ?[3]
- Las matrices cuyo determinante es igual a 5.
- Las matrices diagonales de .
- Las matrices triangulares superiores que no tienen ceros en la diagonal.
- Las matrices cuyos determinantes son 1 o .
- Para cada uno de los grupos siguientes, producir una lista completa de sus subgrupos.
- Los Enteros con la adición.
- Los Enteros Pares con la adición.
Propiedades de los Subgrupos.
[editar]La siguiente proposición afirma que la relación entre subgrupos es transitiva. Proposición 3. (Transitividad de la relación de ser subgrupo) Sean , y subgrupos de un grupo . Si es subgrupo de y es subgrupo de entonces es subgrupo de
-
Demostración: Ejercicio.
Proposición 4. Intersección de Subgrupos La intersección de dos subgrupos es un subgrupo.
-
Demostración: Sean K, K' subgrupos de un grupo G y sea H la intersección de K con K'. Como el elemento neutro esta en K y K', dicho elemento está en su parte común H. Luego, H no es vacío. Sean x, y elementos de H. Entonces, x, y pertenecen tanto a K como a K'. Como K (resp. K') es un subgrupo de G, tenemos que esta en K (resp. en K'). Por lo tanto, está en la parte común H. Luego H < G.
El Centro de un Grupo
[editar]Definición. (Centro de un Grupo) Sea un grupo. Llamamos centro del grupo al subconjunto denotado por y formado por todos los elementos de que conmutan con cualquier otro elemento de .
Proposición 5. El centro de un grupo es un subgrupo abeliano del grupo.-
Demostración: Como el elemento neutro conmuta con todos los elementos del grupo, el neutro está en Sean , elementos del centro. Entonces, para todo de tenemos que
por lo que está en . Notemos, además, que
Es decir que en implica que está en . Por lo tanto,
El tamaño relativo del centro indica cuan abeliano es un grupo. Claramente, si es abeliano, entonces . Cuando , el único elemento que conmuta con todos los otros es el neutro .
Ejemplo. (Centro del grupo simétrico S3).
El grupo S3 está caracterizado por tener dos generadores a, b tales que a3 = b2 = e, bab = a2. Como las potencias de a conmutan entre si, veamos que pasa con b. La tercera condición implica que ba =a2b, es decir que b no conmuta con a. Por su parte, ba2 = baa = a2ba= a2+2 b = ab. Por lo tanto, Z(S3) = {e}.
Ejemplo (Centro del grupo lineal ).
Supongamos que fuera un elemento del centro de G. Sea . Entonces, y Si A está en el centro de G, AU = UA, comparando las entradas de cada uno de esos productos, tenemos que
- (1,1) ==> a = a+c,
- (1,2) ==> a+b = b + d,
- (2,1) ==> c = c y
- (2,2) ==> c+d = d.
Luego, c = 0, a=d. Tomando y computando AV = VA se concluye que b=0. Por lo que las únicas matrices en el centro del grupo lineal son las matrices escalares, los dos numeros de la diagonal son iguales y no nulos (el determinante no puede ser cero), y los números fuera de la diagonal son nulos. Es fácil probar que esas matrices (matrices escalares) conmutan con todas las otras matrices y por lo tanto forman el centro de G
Ejercicios
[editar]- Probar la proposición sobre la transitividad de la relación "ser subgrupo".
- Probar la siguiente generalización de teorema de intersección de dos subgrupos.
- Sea una familia de subgrupos de un grupo G. La intersección H de los subgrupos de la familia es también un subgrupo de G</math>.
- ¿Cuál es la intersección de todos los subgrupos de un grupo?
- ¿Es igual la intersección anterior a la intersección de todos los subgrupos propios?
- (Subgrupos de los Enteros) Sabemos que cada subgrupo no nulo de los Enteros es cíclico y tiene un generador positivo.
Hallar un generador positivo de cada uno de los siguientes subgrupos de .
- .
- .
- .
- ¿Qué podemos decir del subgrupo ?
- En , hallar la intersección de los subgrupos cíclicos y .
- Hallar el centro del producto . (Sug. La respuesta es fácil.)
- Hallar el centro del producto .
- Probar que las permutaciones en (permutaciones de ) que fijan al 4 forman un subgrupo isomorfo a . Generalizar el resultado anterior para Sn.
Los Homomorfismos y los Subgrupos
[editar]En esta sección, veremos como un homomorfismo entre dos grupos relaciona a los subgrupos de uno de ellos con los subgrupos del otro.
Proposición 6. (Homomorfismos y Subgrupos) Sea un homomorfismo de grupos.
- Si H es un subgrupo de G, su imagen, f(H) es un subgrupo de G'.
- Si H' es un subgrupo de G', su preimagen (o imagen inversa), es un subgrupo de G.
-
Demostración:
- La imagen directa de contiene al menos a por lo que no es vacía. Sean elementos de . Por definición de imagen directa, hay elementos y en tales que y Entonces, Como es un subgrupo, está en , de donde está en lo que prueba que es un subgrupo de
- Notemos que como cada subgrupo contiene al neutro, no es vacío ya que contiene a , ya que está en Sean , elementos de o sea tales que y están en . Por lo tanto, también está en ; lo que prueba que está en , de donde el resultado.
- Es decir que Por lo tanto,
- Lo que prueba que la correspondencia es un homomorfismo. La inyectividad de la correspondencia sigue de la propiedad cancelativa. Luego, G es isomorfo a .
- Sea el supramorfismo canónico que asigna a cada entero x su clase .
- Evaluar f(256), f(-256), f(1000).
- Sea . Sabemos que f(H) es un subgrupo de Determinarlo.
- Sean , los subgrupos de generados por respectivamente. Describir los subgrupos y de los Enteros.
- Describir el núcleo de f.
- Sea un homomorfismo de grupos tal que . Probar que f es un homomorfismo. Hallar la imagen de f, y el núcleo de f.
- Sea un homomorfismo de grupos, donde H es un grupo abeliano. Sea (conmutador de x, y). Probar que z está en el núcleo del homomorfismo.
- Notemos que en un grupo abeliano, la conjugación por cualquier elemento es la función identidad.
- Notemos (de la demostración anterior) que la función c:G --> Aut(G) tal que c(g) = cg es un homomorfismo de grupos, que puede verificarse es un monomorfismo.
- (Geometría) Una rotación del plano por un cierto ángulo alrededor del punto P es conjugada de rotación por el mismo ángulo alrededor del origen. El elemento que produce la conjugación es la traslación que envía el origen en el punto P. Este tipo de conjugación es muy importante en la geometría, pues permite transportar situaciones alrededor de un punto P al origen.
- Notemos que Es decir que cuando es un elemento del centro, todos sus conjugados son igual a él mismo. Luego, para todo , (conjunto de conjugados por de elementos del centro) es igual a .
- Sea H un subgrupo de un grupo G. Para todo g en G, es un subgrupo que es conjugado a H.
- .
- Una congruencia del plano es una transformación que preserva distancia entre puntos. Es decir que es una congruencia, ssi, para todo par de puntos , se cumple que
- Una traslación por un vector , es una función del plano en si mismo denotada por y tal que .
- Una rotación alrededor de un punto es una congruencia del plano que deja fijo solamente al punto . Es decir que, implica que .
- Una reflexión alrededor de una línea es una función del plano en si mismo que envía cada punto en un punto ubicado en la línea perpendicular a y que pasa por de modo que el punto medio entre y esté en la línea .
- Lo que prueba que la composición de dos congruencias es una congruencia.
- Lo que prueba que la inversa de una congruencia es una congruencia.
- (Propiedades de las Traslaciones)
- Las traslaciones son congruencias.
- Dados puntos P y Q del plano, hay una única traslación que envía P en Q.
- El conjunto formado por todas las traslaciones determina un subgrupo abeliano del grupo euclídeo. (Sug. Evaluar .)
- El conjunto de congruencias que fijan el punto P (f(P)=P), , es un subgrupo del grupo de las congruencias.
- Sea f una congruencia que fija el origen. Probar que f preserva largos. ()
- Sea f una congruencia que fija el origen y sea la traslación que envía el origen en A. Entonces, es una congruencia que fija el origen.
- Sean transformaciones lineales con matrices asociadas y . La composición es lineal com matriz asociada igual al producto de las matrices.
- (Propiedades de las Rotaciones) Las rotaciones son congruencias. Las rotaciones alrededor del origen determinan un subgrupo de las congruencias.
- Sea el conjunto formado por todas las rotaciones alrededor del punto . Probar que ese conjunto determina un grupo contenido en el grupo euclídeo.
- Sea una rotación alrededor del origen del plano y sea un punto cualquiera. Entonces, es una rotación alrededor de . La correspondencia define un isomorfismo entre esos grupos de rotaciones.
- Determinar cuáles de los siguientes enunciados son válidos y cuáles son falsos
- En cada subgrupo, la operación es asociativa.
- En cada subgrupo, la operación es conmutativa.
- Cada grupo es un subgrupo de si mismo.
- Todo grupo tiene subgrupos propios.
- Los subgrupos cíclicos son siempre subgrupos propios.
- es un subgrupo cíclico de .
- Probar que en un grupo abeliano G, .
- ¿Será valido el resultado del ejercicio anterior, si reemplazamos 2 por un n cualquiera?
- Un subconjunto finito cerrado respecto a la operación de un grupo es un subgrupo.
- ¿Cierto o falso? Un grupo cuyos subgrupos propios son todos abelianos es abeliano.
- Sea , matrices invertibles 2 x 2 con entradas en . Por lo que los posibles valores de los determinantes de esas matrices son [1], [2], [3] y [4]. Se sabe que el orden de G es 480 y se quiere conocer el orden de , las matrices invertibles 2 x 2 cuyo determinante es [1].
- Sea . Probar que .
- Sea A en G, probar que .
Usar lo anterior para responder la interrogante.
- Sea G un grupo y a un elemento de G. El conjunto es un subgrupo.
- (Generalización del ejercicio anterior) Sea G un grupo y S un subconjunto de G. El conjunto es un subgrupo. (Hay una demostración fácil usando el resultado anterior y un teorema del texto.)
- Sea G un conjunto y definamos , ssi, . Probar que se trata de una relación de equivalencia.
- Para cada uno de los grupos siguientes, producir una lista completa de sus subgrupos.
- Los Enteros con la adición.
- Los Enteros Pares con la adición.
- Sea el conjunto de funciones desde un conjunto no vacío en los Reales. Si y son elementos de , se define suma y producto tales que y
- Probar que es un grupo abeliano, mientras que es solamente un monoide abeliano.
- Suponer que . Una función es par (resp.impar), ssi, para todo , (resp. ). Probar que las funciones pares (resp, impares) determinan un subgrupo aditivo de
- ¿Qué pasa con respecto a la multiplicación?
- (Cálculo) Sea el grupo aditivo formado por todas las funciones de en . Sea el subconjunto de formado por las funciones continuas y sea el subconjunto de formado por las funciones derivables. Probar que es subgrupo de <>math>\mathcal C</math>, que a su vez es subgrupo de .
- (Semigrupos y Monoides) Definir las nociones de subsemigrupo y submonoide. Enuciar teoremas semejantes a los de subgrupos y probarlos. Aplicar sus definiciones al monoide M cuya tabla de operaciones se indica.
- Sean H = {a,b} y K = {b,c}.
- Cuál es el neutro de M?
- Verificar que H y K con la operación restringida son monoides.
- Su definición de submonoide debe servir para verificar que H es un submonoide de M, pero que K no lo es.
- Un grupo (o subgrupo) cíclico consiste de todas las potencias enteras de uno de sus elementos, llamado generador del grupo.
- Los grupos cíclicos son abelianos.
- Dos grupos cíclicos finitos de igual orden, son isomorfos. Denotamos a un grupo cíclico de orden n por Cn .
- Hay grupos cíclicos finitos (Enteros módulo m) e infinitos (los Enteros).
- Cada elemento de un grupo cualquiera genera un subgrupo cíclico, denotado por .
- . En este caso, . Esto implica que f es inyectiva. Como f es, además, suprayectiva, tendremos que f establece un isomorfismo entre el grupo aditivo y el grupo .
- . En este caso, se cumple que para todo n, . En particular con n = 1, tenemos que a = e. Por lo tanto, ,el subgrupo nulo.
- donde d es un entero positivo mayor que 1. El número d es el menor entero positivo tal que ad = e. Para cualquier otro entero m tendremos entonces que, m=qd+r, con y, por lo tanto, Es decir que
un grupo cíclico con d elementos.
- G es isomorfo al grupo de los Enteros, por lo que es un grupo infinito, o
- G es el subgrupo trivial integrado únicamente por el elemento neutro, o
- G es isomorfo a .
- Sigue de la proposición que grupos cíclicos de orden infinito son isomorfos.
- Los Enteros módulo m, la raíces n--ésimas de la unidad caen en la tercera categoría anterior.
- En el grupo aditivo de los Enteros, cualquier elemento diferente de 0 tiene orden infinito, pero no son necesariamente generadores del grupo.
- Cada subgrupo de un grupo cíclico es cíclico.
- Sea G un grupo cíclico de orden n. Entonces, para cada divisor del orden de G, hay exactamente un subgrupo con ese orden. En forma más precisa, si n=qd y , el subgrupo de orden d es ,
- Sea de orden n. El orden de es n/mcd(k,n).
- Sea G un grupo cíclico. Si G es infinito, el resultado sigue del resultado acerca de los subgrupos del grupo . Si G es nulo, el resultado es trivial. Supongamos entonces que y que el orden de a fuera d>1. Es decir, d sería el menor entero positivo tal que ad=e. Sea H un subgrupo no trivial de G, entonces habrá algún ak en H con . Sea s el entero positivo minimal con la propiedad que as \in H. Afirmamos que H = <as>. Sea ap un elemento cualquiera de H, entonces por el algoritmo de la división de Euclides, aplicado a p y s, nos proveerá enteros q y r tales que: . Notemos que
, lo que muestra que ar es un elemento de H. Por la minimalidad de s, tendremos que r = 0, lo que implica que cada elemento de H es una potencia de as. Es decir que, H = < as es un subconjunto de <as>; como la inclusión inversa es trivial, tendremos que H = <as>, de donde, concluimos que H es cíclico. - Sea G un grupo cíclico de orden n y sea d un divisor de n, digamos que n = qd. Probaremos que <aq> tiene orden d. En efecto, se tiene que (aq)d = aqd = an = e, o sea que d debe ser un múltiplo del orden de aq. Supongamos que k fuera el orden de aq, si k fuera menor que d, se tendría que aqk} = (aq)k = e. Como qk < qd = n, lo anterior es imposible, ya que n es el menor entero positivo p tal que ap=e. Luego, k debe ser igual a d. Probaremos ahora la unicidad, sean d y q como antes y sea H un subgrupo de orden d de G, queremos probar que H= q. Sabemos que H es cíclico y que, por lo tanto, existe un s tal que H = s>; como an = e, se tiene que s es un divisor de n y, por los argumentos anteriores, el orden de a debe ser igual a n/s. Pero ese orden es d = n/q. Luego n/s=n/q, de donde s=q y queda probada la unicidad.
- Sea d= mcd(k,n). Entonces k=k1d y n=n1d. Luego,
Pero, , por lo que . Sigue de la caracterización del orden por divisibilidad que o - (Puntos fijos de una permutación) Llamamos punto fijo o elemento fijo por (o de) una permutación en a un punto de tal que . Hay ejemplos de permutaciones y de transformaciones que no tienen puntos fijos, mientras que la identidad deja a todos los puntos fijos. En el ejemplo A, los puntos fijos son 3 y 5.
- (Soporte de una permutación.) Llamamos soporte de la permutación al subconjunto de formado por todos los elementos de que no quedan fijos por .
En otras palabras, el soporte de una biyección es el complemento (como conjunto) del conjunto de elementos fijos por . Coloquialmente, decimos que la permutación \textit{mueve} a los puntos de su soporte.
El soporte del permutación del ejemplo B es .
- Un ciclo de largo 1 indica que todos los elemento de quedan fijo por la permutación, o sea que se trata de la identidad.
- Una permutación puede dar origen a uno o más ciclos.
- Si , entonces el soporte de es precisamente .
- Llamamos \textit{permutación cíclica} de al ciclo de . \index{permutación!cíclica}
- Sea un --ciclo. Se tiene que
Observemos que .
- Sean , y permutaciones de , con , y . Expresar cada una de esas permutaciones como un producto de permutaciones disjuntas.
- Sean , , y permutaciones de . Expresar cada uno de esos ciclos en la forma matricial.
- Sean , , y permutaciones de . Realizar las operaciones indicadas.
- Suponer que las permutaciones son de . Sea . Hallar , , , , y . Probar, además, que .
- Suponer que las permutaciones son de . Sean , y .
- Probar que los cuadrados de esas transposiciones son la identidad.
- Probar que cada una de esas transposiciones tiene un inverso igual a ellas mismas.
- Simplificar .
- Simplificar .
-
- Sea una transposición de . Probar que y que .
- Sea un 3--ciclo de . Probar que y que .
- ¿Cómo se podrían generalizar lo anterior a --ciclos de ? Conjeturar y tratar de probar.
- Probar que en , se tiene las siguientes relaciones:
- .
- .
- .
¿Qué se puede conjeturar?
- Construir la tabla de , el grupo simétrico del conjunto . Comparar la tabla del grupo con la tabla de la multiplicación de .
- Verificar la tabla de . Determinar todos los subconjuntos cerrados de . Comparar la tabla de con la tabla de las simetrías de un triángulo equilátero .
- Sea un subgrupo de un grupo simétrico y sean . Probar que el conjunto de permutaciones en que fijan , es un subgrupo de denotado por .
- es un ciclo tal que (subíndices computado los índices mayores que módulo ) .
- Si entonces es un -ciclo.
- Si entonces es un producto de ciclos de largo
- Como , tenemos la parte a).
- Cuando , entonces para todo , , los enteros
son enteros diferentes módulo .
En efecto, si , se tendría que . Como no divide a , se tiene que .
- Cuando , se tiene que . Lo que prueba la afirmación sobre el orden de . El resto sigue de forma inmediata.
- El orden de es 30.
- Expandir como una permutación completa de cinco elementos, cada uno de los siguientes ciclos de .
- Probar que en , se tiene las siguientes relaciones:
- .
- .
- .
¿Qué se puede conjeturar?
- Hallar todos los ciclos de largo 3 en y en .
- Probar que y que .
- Sea un producto de transposiciones disjuntas. Probar que .
- Sea . Probar que donde los subíndices mayores que se computan módulo . Por ejemplo, Usar lo anterior, para computar rápidamente los siguientes cuadrados: , , , . Observar que no siempre el cuadrado de un ciclo produce un ciclo del mismo largo. Inventar un método para calcular cubos de permutaciones rápidamente.
- Sean y permutaciones disjuntas de . Probar que
- y son permutaciones disjuntas, y que
- .
- \label{exDCT} Probar que . Es decir que todo ciclo es un producto de transposiciones.
- Probar que en , Si y son ciclos disjuntos, entonces .
- Sean , , , y . Verificar que
- Sea donde es un producto de ciclos disjuntos de . Sea . Probar que y que .
- Sea donde es tal que . Sea . Probar que y que .
- Hallar la cantidad de 2--ciclos en .
- Probar que el soporte de un ciclo es la órbita de cualquiera de los elementos del ciclo por .
- Para cada grupo indicado, hallar el subgrupo cíclico generado por el elemento indicado
- Describir al subgrupo cíclico de generado por las matrices siguientes.
- Sea .
- ¿Por qué este grupo es cíclico?
- Hallar todos los posibles ordenes de elementos de G.
- Para cada divisor d de 12, hallar un elemento de G con orden igual a d.
- ¿Cuáles son todos los generadores de ?
- Hallar los automorfismos de .
- Sea G un grupo finito. Sean a y b elementos de G. Probar las siguientes relaciones acerca de sus ordenes.
- o(a-1)= o(a).
- o(bab-1) = o(a).
- Si ab=ba entonces o(ab) = mcm(o(a), o(b)).
- Si mcd(o(a),o(b)) = 1 y ab =ba entonces o(ab)=o(a)o(b).
- Hallar la cantidad de generadores de para
- Probar que el grupo multiplicativo para m=5 y 7 es cíclico, pero que no es cíclico.
- Sea de orden Probar que , ssi, .
- Sea f: G --> H un homomorfismo de grupos con G = <g> y H = <h>. Probar que o(h) es un divisor de o(g).
- Probar que la imagen por un homomorfismo de un grupo cíclico es un grupo cíclico. ¿Cuál es uno de los generadores de este grupo cíclico? ¿Puede pasar que el grupo original sea infinito, pero que su imagen sea un grupo finito?
- Sea G un grupo cíclico infinito. Probar que si G es un generador del grupo, hay solamente otro generador, que es el inverso de G. ¿Será cierto que un grupo cíclico con exactamente dos generadores es infinito?
- Sea G un grupo cíclico que tiene un único generador. Probar que G tiene solamente dos elementos.
- (Producto de Grupos Cíclicos)
- Sea H el grupo cíclico de orden 5 generado por a y sea K el grupo cíclico de orden 3 generado por b. Probar que el producto es un grupo cíclico generado por (a,b). Concluir que .
- Sea H el grupo cíclico de orden 4 generado por a y sea K el grupo cíclico de orden 2 generado por b. Probar que el producto no es un grupo cíclico.
- ¿Cuándo el producto de grupos cíclicos es cíclico?
- Sea p un número primo. Probar que f(pn)=pn-1(p-1), donde f es la función de Euler. (Sugerencia. mcd(a,pn=1, ssi, mcd(a,p)=1.)
- (La función f de Euler). Probar que para cada entero positivo n se cumple que . (Sugerencia: considerar el grupo cíclico con n elementos y la cantidad de generadores de cada uno de sus subgrupos.)
- Probar que Un (raíces enésimas de la unidad) es un grupo cíclico de orden n respecto a la multiplicación de números complejos.
- Marcar cada uno de los siguientes enunciados como válido o falso.
- Un grupo abeliano es un grupo cíclico.
- Un grupo cíclico de orden 30 tiene un subgrupo de orden 12.
- Un elemento x de un grupo G tiene orden n, ssi,
- Los Racionales positivos con la multiplicación forman un grupo cíclico infinito.
- Cada elemento diferente del neutro es un posible generador de un grupo cíclico.
- ¿Cuáles grupos cíclicos tiene la propiedad que cualquier elemento diferente del neutro es un generador del grupo?
- (Monoides) Un monoide es cíclico cuando todos sus elementos son potencias naturales de un elemento m, y . ¿Cuáles resultados de grupos cíclicos se podrían extender a monoides cíclicos?
- (*) Se prueba en el texto que para cada divisor del orden de un grupo cíclico, hay exactamente un subgrupo de ese orden. ¿Caracteriza esta propiedad a los grupos cíclicos? Es decir, si sabemos que un grupo finito tiene para cada uno de los divisores de su orden exactamente un subgrupo de orden dicho divisor, ¿podremos concluir que el grupo es cíclico?
- Cada grupo abeliano finito es un producto de grupos cíclicos.
- Sea G un grupo abeliano de orden . Entonces, hay una sucesión de enteros positivos mayores de 1 tales que cada número de la sucesión es un divisor del próximo y cuyo producto es , tal que G es el producto de los . Además dicha sucesión es única. [4]
- Grupos abelianos de orden 8.
Los divisores positivos de 8 (mayores que 1) son 2, 4, 8. Por lo que tenemos las siguientes sucesiones posibles:(2,2,2), (2,4) y (8). Luego hay tres tipos posibles de grupos abelianos de orden 8.
- Grupos abelianos de orden 10. Los divisores positivos de 10 (mayores que 1) son 2, 5 y 10. Por lo que la única sucesión posible satisfaciendo las condiciones de divisibilidad es 10. Es decir que hay solamente un grupo abeliano de orden 10, el grupo cíclico de orden 10.
- Grupos abelianos de orden 20. Los divisores positivos de 20 (mayores que 1) son 2, 4, 5, 10 y 20. Luego, las únicas sucesiones satisfaciendo las condiciones de divisibilidad son 20 y 2, 10. Es decir que los únicos grupos abelianos de orden 20 son el grupo cíclico de orden 20 y el producto
- Wikipedia: Grupo Cíclico
- Wikipedia: Aritmética Modular
- Weisstein, Eric W. "Cyclic Group." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CyclicGroup.html
- ↑ Por parámetros u operaciones de una estructura, nos referimos a todos los componentes de la misma diferentes del conjunto base.
- ↑ Véase el apéndice Teoría de Estructuras Algebraicas.
- ↑ Si no tiene mucha familiaridad con matrices, poner n=2.
- ↑ Ver, por ejemplo (BB) Dean pag. 152.
- Supongamos el resultado válido para productos de elementos con la propiedad indicada y consideremos ahora un producto de elementos: . Por la hipótesis de inducción, el producto de los primeros elementos es un elemento de Como el producto total es igual a , se concluye que el producto está en El resultado sigue por inducción.
- En particular, un grupo es un grupo generado por un subconjunto cuando lo sea como subgrupo de si mismo.
- Notemos que cuando contiene un solo elemento, es el grupo cíclico generado por ese único elemento.
- Cuando la notación es aditiva, está formado por todas las sumas cuyos sumandos son elementos de u opuestos aditivos de elementos de
- Decimos que el grupo está finitamente generado, cuando sea un conjunto finito.
- De acuerdo al convenio indicado, el subgrupo generado por el conjunto vacío es el subgrupo trivial {e}.
- Los grupos cíclicos son grupos generados por un elemento.
- El conjunto de generadores no es único.
Por ejemplo, el grupo cíclico es generado por pero también por ya que
- Recorra la lista, cuando haya una inversión, intercambie los objetos correspondientes.
- Si no se hallan inversiones, la lista está ordenada.
- Volver al inicio de la lista y efectuar el paso 1.
- es un producto de transposiciones simples.
- es la menor cantidad de transposiciones simples necesarias para escribir como un producto de transposiciones simples.
- La función signo es un homomorfismo suprayectivo de grupos, cuando
- Si entonces Es decir que la función signo es constante en las clases de conjugación de
- Es decir que Lo que prueba el resultado. Como vimos en el ejemplo, cuando lo que prueba la suprayectividad.
- Como se tiene el resultado.
- Las transposiciones tienen signo
- Cuando es un --ciclo, su signo es
- El grupo es un subgrupo de índice 2 en
- Como los 3--ciclos son permutaciones pares todos ellos están contenidos en
- Transposiciones disjuntas.
- Transposiciones no disjuntas,
- Hallar la descomposición en ciclos disjuntos de cada uno de los elementos de Determinar además para cada uno de ellos.
- Expresar como producto de ciclos disjuntos a
Hallar
- Verificar las relaciones siguientes.
Conjeturar un resultado que establezca una relación entre transposiciones y transposiciones simples, probando de esta manera que las transposiciones simples generan al grupo simétrico.
- Escribir cada una de las permutaciones siguientes como un producto de transposiciones simples. \smallskip\setcounter{ejt}{0} \begin{tabular}{lp{1.8in}ll} \nejt & &% \nejt & \\ \nejt & &% \nejt & \\ \end{tabular}
- Sea igual al producto de cinco transposiciones simples disjuntas. Hallar
- Sea y sea Hallar
- Probar que el orden de es divisible por 8, pero no hay elemento de orden 8 en ese grupo.
- Listar todos los ordenes posibles para los elementos de y hallar elementos de cada uno de ese orden.
- Probar que no tiene un elemento de orden 13, pero sí tiene un elemento de orden 60.
- Sea un número primo menor que Hallar la cantidad de subgrupos de orden de
- Probar las siguientes afirmaciones:
- La cantidad de --ciclos en es
- La cantidad de --ciclos en es
Generalizar para --ciclos.
- Sea un grupo con generadores tales que
- , cuando
Entonces,
- y
- Decimos que un punto de es fijo por o que fija a ssi,
- Decimos que un subconjunto es fijo puntualmente por o que fija puntualmente a ssi, cada punto de es fijo por
- Decimos que un subconjunto es fijo (globalmente) por o que fija puntualmente a ssi,
- los vértices están identificados como B, y en ambas caras del cuadrado;
- el cuadrado está sobre una superficie fija y hemos marcado los bordes del cuadrado sobre esa superficie y copiado las etiquetas de los vértices;
- el cuadrado está sujeto a la superficie por un alfiler colocado en su centro, de manera que pueda rotar libremente alrededor del alfiler.
- Las matrices y definen transformaciones (biyectivas) del plano, ya que sus determinantes no son nulos.
- Sea Entonces,
- Sea Entonces,
Es decir que es una congruencia del plano.
- Se tiene que De manera análoga a lo hecho con se verifica que define una congruencia del plano.
- Por la parte b) se tiene que
Por lo tanto, es una simetría del cuadrado.
- Es fácil ver que y
- Observando los resultados anteriores tenemos que
por lo que tiene orden 4.
Por su parte tiene orden 2. Finalmente, tenemos que:
- Construir el grupo de simetrías de un triángulo equilátero y verificar que es isomorfo a
- Sea un grupo de transformaciones de un conjunto ( o sea , un subgrupo del grupo simétrico de
- Las transformaciones que fijan un punto determinan un subgrupo de
- Sea las trasformaciones que fijan globalmente un subconjunto de Probar que es un subgrupo de que contiene como subgrupo a las transformaciones que fijan puntualmente.
- Sea un punto fijo de Entonces, es un punto fijo de
- Sean y
Sea el polígono regular con vértices \ldots ubicados en la circunferencia unitaria del plano cartesiano de modo que
Probar las siguientes afirmaciones.
- y son congruencias del plano.
- es una rotación por un ángulo que mide radianes.
- es una reflexión entorno al eje
- El orden de es y el orden de es 2.
- El grupo de matrices generados por y es isomorfo al grupo diedral
- (*) Construir el grupo de simetrías del tetraedro regular.
- (*) Construir el grupo de simetrías de un cubo.
- Llamamos (conjunto) producto de con al conjunto denotado por y que está formado por todos los productos tales que está en y está en B. Cuando o consistan solamente de un elemento, escribiremos solamente el elemento; por ejemplo, si escribiremos en lugar de Cuando la notación es aditiva, simbolizamos por al conjunto formado por todas las sumas de un elemento de con un elemento de B.
- denotará al conjunto formado por los inversos de los elementos de
Notación Aditiva: (los opuestos aditivos de todos los elementos de
- En forma general, denotará el conjunto de las potencias enésimas de elementos de Notación aditiva: (todos los múltiplos de elementos de A.).
- Decir que es una parte cerrada de es equivalente a decir que es un subconjunto de
- Análogamente, decir que es cerrado respecto a inversos, es equivalente a decir que es un subconjunto de
- Decir que es un subgrupo de es equivalente a decir que no es vacío y que es un subconjunto de
- Decir que es equivalente a decir que para cada de hay un en tal que
- Sea Hallar los elementos de los conjuntos indicados, cuando
- Sea y sean Hallar los conjuntos indicados.
- Sean subconjuntos de un grupo cualquiera. Entonces,
Definición. (Núcleo de un homomorfismo)) Llamamos núcleo de un homomorfismo al subgrupo de
Simbolizamos ese subgrupo por . (ker, del alemán kernel). Con ayuda de la noción de núcleo, podemos caracterizar a los monomorfismos (homomorfismos inyectivos).
Proposición 7. (Caracterización de Monomorfismo) Un homomorfismo es un monomorfismo (o sea inyectivo), ssi, el núcleo es el subgrupo trivial
-
Demostración: () Supongamos que Se tiene entonces que
Por lo que pertenece al núcleo. Como el núcleo solo contiene al , tenemos que , de donde ; es decir que es inyectiva.
() Sea .Entonces, lo que implica, ya que es inyectiva, que . Es decir que
Corolario 7.1. Los isomorfismos tienen núcleos triviales .
Sigue de las proposiciones anteriores que cuando es un homomorfismo de en entonces es un subgrupo de . Además que el homomorfismo establece una correspondencia biunívoca entre los subgrupos de que contienen al núcleo y los subgrupos de , En particular, cuando se trate de un isomorfismo habrá una correspondencia biyectiva entre ambos conjuntos de subgrupos.
Teorema de Cayley
[editar]Arthur Cayley, mencionado antes como el creador de la noción abstracta de grupos, probó que todo grupo finito puede presentarse como un subgrupo de permutaciones, más precisamente, es isomorfo a un subgrupo de un grupo de permutaciones. La idea del isomorfismos es asociar con cada elemento del grupo una permutación de los elementos del grupo. Para simplicidad de la nomenclatura, acordamos lo siguiente,
Definición. Llamamos grupo de permutaciones a cualquier subgrupo de un grupo simétrico Sn.
Consideremos un grupo finito G y un elemento cualquiera g de G. Sea Lg la función de G en G tal que Lg(x) = gx (es decir la multiplicación de g por la izquierda ).Lema. es una permutación del conjunto G.
-
Demostración: Si , de donde por la propiedad cancelativa, obtenemos que ; o sea que la función Lg es inyectiva. Probaremos ahora que es suprayectiva. Sea y un elemento cualquiera de G, entonces , lo que prueba que la función es suprayectiva, es decir que se trata de una función biyectiva, o sea de una permutación o elemento de . Mostremos ahora que la correspondencia es un homomorfismo de grupos. En efecto,
Hemos probado el siguiente teorema.
Teorema de Cayley Todo grupo finito es isomorfo a un grupo de permutaciones.
Ejercicios
[editar]Subgrupos Conjugados
[editar]La conjugación (definición a continuación) provee a un grupo no abeliano con una familia no trivial de automorfismos.
Definición. (Conjugación) Sea un grupo y g un elemento cualquiera de . Llamamos conjugación por a la función de en si mismo, denotada por , tal que
Decimos que dos elementos , son conjugados entre si (notación: ), cuando hay un tal que .
Decimos que los subconjuntos y son conjugados, ssi, hay un tal que . En particular, dos subgrupos son conjugados, cuando lo son como subconjuntos.
Proposición 8. (Conjugación es un Automorfismo) Sea un grupo, es un automorfismo de , o sea un isomorfismo de en si mismo.-
Demostración: Tenemos que , lo que prueba que se trata de un endomorfismo.
Notemos, además, que
Corolario 8.1. Las conjugaciones determinan un subgrupo del grupo de automorfismo, llamado el grupo de automorfismos interiores.
-
Demostración: Observemos que . Es decir que la composición de conjugaciones es una conjugación. Como, claramente , se tiene el resultado.
Observaciones.
Clases de Conjugación
[editar]Sean , escribimos para indicar que x es conjugado con y. Es fácil ver que es una relación de equivalencia en G, cuyas clases de equivalencia llamaremos clases de conjugación.
En un grupo abeliano, las clases de equivalencia consisten de un único elemento.
Ejemplo (Las Clases de Conjugación de S3).
Sea . Se verifica, por computación directa, que las clases de conjugación son
Ejemplo.
Sea y sea .
Buscaremos subgrupos de S3 que sean conjugados con H.
Como esos son todos los subgrupos de orden 3 se tiene el resultado.
Subgrupos Geométricos
[editar]<<<EN PREPARACIÖN>>> Sea el plano cartesiano que identificamos con , el conjunto formado por todos los pares ordenados del plano. El plano está provisto de una estructura de producto de grupos, , la suma componente por componente, o sea, tal que
Además, hay una multiplicación por escalar, que asocia a cada número real (escalar) y a cada par (vector), el vector . En este contexto, usualmente, se dice que los puntos son vectores y los números reales, . Se define el largo del vector como.
y la distancia entre puntos como el largo de la diferencia o seaDenotaremos por al grupo formado por todas las biyecciones del plano en si mismo, la operación siendo la composición de funciones. (Es decir, el grupo simétrico del plano). Llamaremos transformaciones (del plano) a los elementos de ese grupo
Mostraremos que el conjunto de todas las congruencias determina un subgrupo de Biy(, llamado el grupo euclídeo del plano, al que simbolizaremos por .
Claramente, la identidad es una congruencia, por lo que el conjunto de las congruencias no es vacío.
- Sean congruencias del plano.
Transformaciones Lineales
[editar]Una transformación lineal es una transformación que envía el punto (x,y) en (x', y') donde
La definición es equivalente a la ecuación matricial,
La condición implica que la matriz tiene determinante no nulo, o sea que es invertible. La matriz se llama la matriz asociada a la transformación lineal. Cada matriz define por la ecuación anterior una transformación lineal. Por lo que el conjunto de las transformaciones lineales (biyectivas) es precisamente el grupo lineal .
Una rotación alrededor del origen es una transformación lineal cuya matriz tiene la forma
donde es el ángulo de la rotación.
Ejercicios
[editar]Probar las afirmaciones siguientes.
Ejercicios del Capítulo
[editar]7. Los Grupos Cíclicos
[editar]Introducción
[editar]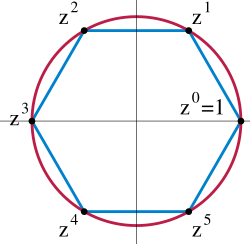
Las seis raíces complejas 6-ésimas de la unidad forman un grupo cíclico bajo la multiplicación. z es un elemento de este grupo cíclico o elemento primitivo, pero z2 no lo es, porque las potencias impares de z no son representables como potencias del elemento z2. Los grupos cíclicos han aparecido varias veces anteriormente. Tales grupos son muy importantes en la teoría de los grupos, especialmente de los grupos abelianos. Dedicaremos este capítulo a establecer la estructura interna de los grupos cíclicos y algunas propiedades no vistas anteriormente.
Resumimos, a continuación, nuestro conocimiento de grupos cíclicos
¿Qué más nos interesaría conocer?
¿Cuántos subgrupos tiene el grupo cíclico Hay grupos cíclicos finitos de cualquier orden, ¿pasa lo mismo con los sugrupos de un grupo ciclíco? ¿Cómo es el grupo de automorfimos de un grupo ciclíco?Clasificación de los Grupos Cíclicos
[editar]En esta sección produciremos un listado completo de todos los posibles grupos cíclicos.
Sea G un grupo cíclico, digamos que . Entonces, para cada entero n, an es un elemento de G, por lo que podemos definir una función f desde los Enteros en G por f(m) = am. Claramente, f es suprayectiva y, por las propiedades de las potencias, tenemos que:
Es decir, que f es un homomorfismo (suprayectivo) de en G. Por los resultados sobre homomorfismos, tendremos que el núcleo de este homomorfismo, o sea el conjunto de todos los enteros n tales que f(n) = an = e, es un subgrupo de . De acuerdo a los resultados de un capítulo anterior, sabemos que los únicos subgrupos aditivos de los Enteros son los (múltiplos enteros de un número positivo o cero m). Por lo que el núcleo de f será uno de esos subgrupos. Tenemos varias posibilidades para ese núcleo, dependiendo de su generador. Proposición 1. (Clasificación de los Grupos Cíclicos) Sea . Tenemos tres posibilidades para G.
Observaciones.
Orden de Elementos
[editar]Ejemplo.
Sea G= . La tabla siguiente presenta los ordenes de cada uno de sus elementos.
Ejemplo de verificación: o([3]) = 4 ya que 4[3] = [12] = [0] y, 1[3] = [3] [0], 2 [3] = [6] [0] y 3[3] = [9] [0]. Notemos que cualquier elemento cuyo orden sea 12 es un generador del grupo, es decir, es posible que haya más de un generador de un grupo cíclico.
Proposición 2. (Caracterización del Orden por Divisibilidad) Sea G un grupo y g un elemento de G con orden finito d. Entonces, cuando , se cumple que d es un divisor de n.
-
Demostración: Se tiene que n = qd + r con . Si r fuera positivo, como r = n - dq, se tendría que ar = an-dq = an(ad)-q = e, por lo que ar=e; pero como r < d, esto es imposible. Luego, r = 0, por lo que se tiene el resultado.
Subgrupos de Grupos Cíclicos
[editar]Describiremos, a continuación, las posibilidades para los subgrupos de un grupo cíclico.
Proposición 3. (Subgrupos de un Grupo Cíclico)
-
Demostración:
Orden de los Elementos
[editar]¿Cuáles son los posibles ordenes de los elementos de un grupo cíclico?
Notemos que el orden de un grupo cíclico coincide con el orden de su generador . Si entonces el orden es infinito, mientras que si , , entonces .
Ejemplo.
En el grupo aditivo de los Enteros, cualquier elemento diferente de 0 tiene orden infinito.
Ejemplo.
Sea . La tabla siguiente presenta los ordenes de cada elemento.
Ejemplo de verificación: ya que y, , y . Notemos que cualquier elemento cuyo orden sea 12 es un generador del grupo, es decir, es posible que haya más de un generador de un grupo cíclico.
Proposición 4. (Caracterización del Orden por Divisibilidad) Sea un elemento con orden finito . Entonces, cuando , se cumple que es un divisor de .
-
Demostración: Tenemos, por división, que con . Si fuera positivo, como , se tendría que , por lo que ; pero como , esto es imposible. Luego, , y se tiene el resultado.
La función de Euler.
Sea un grupo de orden . Sigue de la parte c) de la proposición anterior que los elementos de orden de son los tales que . Es decir, todos los , que son relativamente primos con . La cantidad de esos elementos se llama la función de Euler de y se denota por .
Ejemplo.
Si es primo, . Por lo que los generadores de son todos los elementos, excepto el neutro.
La tabla siguiente muestra los valores de para valores pequeños de ,
Homomorfismos y Grupos Cíclicos
[editar]Proposición 5. (Homomorfismos y Cíclicos) Sea G un grupo cíclico y un homomorfismo de grupos. Entonces, la imagen es un subgrupo cíclico.
-
Demostración: Sea un generador de . Entonces, para cada de hay un , para algún , tal que . Lo que implica que ; lo que muestra que es cíclico con generador .
Los Automorfismos de los Enteros Módulo m
[editar]Recordemos que un automorfismo de un grupo es un isomorfismo (homomorfismo biyectivo) del grupo en si mismo. Todos los automorfismo de un grupo determinan, a su vez, un grupo simbolizado por (G). Sea G=, el grupo cíclico con m elementos y sea f: G \flecha G un automorfismo, entonces la imagen de [1] debe ser un generador de G, ya que . Luego, hay posibles selecciones para la imagen de G. Por lo que se tiene que .
Los Grupos Simétricos
[editar]Recordemos que llamamos grupo simétrico de un conjunto al grupo determinado por todas las biyecciones del conjunto en si mismo, con la composición de funciones como operación. Dos conjuntos con igual cardinal tienen grupos simétricos isomorfos.
Cuando el conjunto es finito, es tradicional llamar \textbf{permutaciones} a los elementos del grupo simétrico.
Advertencia. Para simplicidad de la exposición, supondremos que nuestro grupo simétrico de símbolos actúa en . Esto no es realmente una gran restricción, ya que los grupos simétricos de conjuntos con elementos son, siempre, isomorfos entre si. Como la intuición de permutaciones es reordenación, el conjunto donde actúan las permutaciones debe estar ordenado, lo que se traducer en una enumeración como
y al restringirnos a es como que estuviéramos trabajando cono los índices.
Recordemos que denotamos por al grupo simétrico de y llamamos permutaciones (de símbolos) a sus elementos. Intuitivamente, una permutación de una cierta cantidad de objetos es un (re)ordenamiento de los mismos.
Los Ciclos
[editar]Ejemplo A.
Sea una permutación de .
Notemos que la (función) es tal que y .
Es decir que mueve el , y de manera cíclica, mientras que deja fijos a y . Tales permutaciones se llaman \textit{ciclos}, que definiremos de manera general más adelante.
Ejemplo B.
Sea una permutación de . En este caso, los puntos que no se mueven son 3 y 7. ¿Qué pasa con aplicaciones sucesivas de a puntos que no quedan fijos?
En este caso tenemos dos puntos fijos y dos ciclos.
Sea una permutación de un conjunto finito con elementos. Sea un elemento cualquiera de . Consideremos la sucesión obtenida por aplicaciones sucesivas de a un punto de y a sus imágenes.
Como es un conjunto finito, los términos de la sucesión
no pueden ser todos diferentes. Por lo que hay y , con , tales que . Si , entonces , lo que implica que , o sea , lo que es una contradicción ya que . Luego , o sea .
Introduciremos una terminología que nos ayudará a estudiar los ``ciclos de una permutación.
Definición. (Ciclos) Sea un conjunto con elementos. Sea una sucesión de elementos diferentes de , . Llamaremos ciclo (de largo ) o k--ciclo a la permutación de que deja fijo a todos los elementos de que no aparecen en la sucesión y tal que
Es decir que
Simbolizamos por a ese ciclo.
Llamamos transposición a un ciclo de largo 2.
Veremos, más adelante, que cada permutación puede expresarse como un producto de ciclos. Antes, presentaremos algunas nociones que nos ayudarán en el estudio de los ciclos de una permutación.
Observaciones.
Permutaciones disjuntas.
Decimos que dos permutaciones son disjuntas cuando sus soportes lo sean.
Observemos que cuando dos permutaciones son disjuntas, los puntos que una mueva, la otra los deja fijos. Esto implica que el producto de las dos biyecciones es independiente del orden del producto.
Permutaciones disjuntas conmutan.
Observemos que una biyección y su inversa tienen igual soporte. También si y son disjuntas se tiene que
Veremos, a continuación, lo anunciado más arriba.Proposición 6. Cada permutación de es un ciclo o un producto único de ciclos disjuntos, excepto por el orden y 1--ciclos.
-
Demostración: (Por inducción sobre la cantidad de elementos en .)
Si , entonces que es un producto de ciclos disjuntos de largo 1.
Sea y sea en tal que . Sea el menor entero positivo tal que . Sea el ciclo . Sea en , entonces, razonado con el prueba del inverso, . Por lo que fija cada elemento de . Si no está en , entonces , por lo que . Luego, , ssi, . Esto implica que . Por la hipótesis de inducción, tenemos que debe ser igual a un producto de ciclos disjuntos, , que como fijan deben ser disjuntos de . Luego
Veamos ahora la unicidad. Supongamos que . Entonces, . Además, implica que . Cada en pertenece por lo tanto a un único , . Por lo que ya que coincide con en . Es decir que los ciclos quedan únicamente determinados por .
Transitividad de la acción
[editar]Sea un conjunto finito tal que . Dados dos puntos , , sea definida por
Claramente es una permutación de , cuando . Cuando un grupo de permutaciones, tiene la propiedad de que dado , hay un elemento del grupo que envía un punto en el otro, decimos que el grupo \textit{actúa transitivamente} sobre el conjunto.
Veremos, a continuación, que actúa transitivamente en el conjunto de sucesiones de --elementos diferentes de , clásicamente llamadas las --permutaciones de un conjunto con elementos.
Sean y dos sucesiones de elementos diferentes. Sea una sucesión formada por los elementos del complemento de . Sea la sucesión análoga para . Entonces, definimos una función que asigna a cada , el correspondiente . Claramente, tal función es la permutación deseada.
Ejemplo.
Sean , y , entonces una permutación satisfaciendo lo indicado arriba es
Esta construcción será usada más adelante para obtener permutaciones con una asignación parcial de sus valores.
Ejercicios
[editar]Propiedades de los Ciclos de Permutaciones
[editar]Sea un ciclo de largo en , digamos que
Mostraremos que cualquier punto que aparece en el ciclo, definen al mismo ciclo. Es decir que un ciclo no tiene una representación única, ya que cualquiera de los siguientes representa el mismo ciclo.
En efecto, tomemos como punto inicial a , entonces por sucesivas aplicaciones de obtenemos la sucesión
Como , tenemos que la sucesión anterior es
Es decir una sucesión de puntos que aparecen en el ciclo que se inicia en . Además, . Si hubiera un tal que , tendríamos que , de donde , lo que no puede ser. Sea el ciclo de largo que se inicia en . Claramente, el soporte de es igual al soporte de . Además, para cada tenemos que . Es decir que .
Cantidad de -ciclos.
¿Cuántos ciclos hay en de largo , ?Las posiciones en un --ciclo, pueden llenarse de
diferentes maneras. Como cada -ciclo puede escribirse de diferentes maneras, tenemos que
Cantidad de k--ciclos =
Orden de Ciclos.
Sea . Los cómputos anteriores muestran que para todo se cumple que . Si no está en , es fijo por luego . Lo anterior prueba la siguiente proposición.
Proposición 7. Un --ciclo tiene orden como elemento del grupo .
En la terminología de la teoría de grupos, el subgrupo generado por un --ciclo es un subgrupo cíclico de orden . Como hay ciclos de largo , para todo . , tenemos que contiene subgrupos ciclos de orden . La siguiente proposición sigue directamente de la teoría de grupos cíclicos, pero, daremos también una demostración directa
Proposición 8. Sea un --ciclo de . Se cumple que
-
Demostración:
Ejemplo.
Sea . Entonces,
Inversa de un ciclo.
La permutación inversa de un ciclo es un ciclo que hace un recorrido inverso de los puntos del ciclo original.
Notemos que se tiene
Observemos también que la inversa de una permutación tiene el mismo orden y soporte que la permutación. Tales resultados siguen en forma inmediata de la proposición anterior aplicada a .
Conjugado de un Ciclo.
Lema de Conjugación Sea un ciclo de y sea una permutación cualquiera de . Entonces, el conjugado de por , , es el ciclo de igual largo-
Demostración: Sea . Entonces
Además,
Lo que prueba que
Ejemplo.
Sea en . Sea . Entonces, .
Ejemplo.
Sea un transposición de , . Sea una permutación tal que y . Entonces,\
Esto muestra que todos los 2--ciclos son conjugados con el ciclo . Como la relación de conjugación es de equivalencia, sigue que dos transposiciones cualesquiera son siempre conjugadas entre si.
Proposición 9. (Orden de un producto de ciclos disjuntos) Sean y ciclos disjuntos. Entonces, es igual mínimo común múltiplo de y .
-
Demostración: Como y son disjuntos, conmutan entre si. Luego, para cualquier se cumple que . Sea . Supongamos que , que y que . Sea . Entonces,
ya que es un múltiplo de los ordenes de y . Luego .
Si está en , . Luego, ; lo que implica que . Análogamente ,
Luego . Lo que prueba que .
Corolario 9.1. Sea . Entonces el orden de es el mínimo común múltiplo de los ordenes de los factores.
-
Demostración: Inducción sobre .
Ejemplo.
En la permutación tiene orden 6.
Ejemplo.
En hay un elemento de orden 30.
Clases de Conjugación
[editar]Sea una permutación de y sea la descomposición en ciclos disjuntos de incluyendo los 1--ciclos y tal que
( es el largo del ciclo ).
Llamamos tipo de a la sucesión . Notemos que
Luego, cada tipo de una permutación define una partición de .
Como cada conjugado de un ciclo tiene igual largo que el ciclo, sigue que los conjugados de una permutación tienen igual tipo que la permutación. Sean y dos permutaciones de igual tipo con las descomposiciones normalizadas como arriba.
Observemos que el soporte es la reunión disjunta de los soportes de los , . Análogamente para el soporte de . Supongamos que donde . Sea el ciclo correspondiente de . Sea la permutación tal que sobre el soporte de es tal que . Luego, por el lema de conjugación, . Se tiene entonces que
Proposición 10. Dos permutaciones son conjugadas, ssi, tienen igual tipo. Hay tantas clases de conjugación de como tipos, o sea como particiones de .
Ejercicios
[editar]Ejercicios del Capítulo
[editar]Comentarios
[editar]Los grupos cíclicos son los bloques para la construcción de grupos abelianos. Se tiene los siguientes resultados:
La demostración de esos resultados requiere otros resultados que no están cubiertos en este texto. Sin embargo, resulta interesante sus aplicaciones para la clasificación de grupos abelianos finitos.
Lecturas Adicionales
[editar]Véase también
Notas
[editar]
8. Los Grupos Generados
[editar]Introducción
[editar]En este capítulo, generalizamos la noción de grupo cíclico, para considerar grupos generados por un subconjunto arbitrario. Aprovecharemos el capítulo para explorar más cuidadosamente los grupos diedrales y expandir nuestro conocimiento de los grupos simétricos. Veremos también como extender las operaciones entre elementos de un grupo a subconjuntos del grupo. Aprovecharemos lo anterior para ver un criterio para determinar si un grupo es producto de dos de sus subgrupos.
Sea un grupo y sea ¿Qué quiere decir que genera a ? Simplemente que cada elemento de es un producto de potencias enteras de elementos de Por ejemplo, Inclusive, podríamos considerar conjuntos infinitos y formar productos, como arriba, de subconjuntos finitos de La manera matemática de hacer lo anterior será expuesta a continuación.
Subgrupos Generados por Subconjuntos
[editar]Sean un grupo, un subconjunto no vacío de y un subgrupo de Cuando x, y son elementos de tenemos que tanto como y son elementos de Las relaciones anteriores se extienden a productos cualesquiera.
Lema 1. Sean un grupo, un subconjunto no vacío de y un subgrupo de Sean elementos de tales que está en o su inverso está en . Entonces, está en
-
Demostración: (Inducción sobre .) Si , el resultado es trivial.
Lema 2. Sean un grupo, un subconjunto no vacío de Sea el conjunto formado por todos los productos de la forma
donde cada factor o su inverso están en Entonces, es un subgrupo de que es un subgrupo de cualquier subgrupo que contenga a
(Convenio. Diremos que un producto con k=0 factores es el elemento neutro del grupo.)
-
Demostración: Sean , elementos de Claramente, no es vacío ya que contiene todos los elementos de (productos de largo 1). Igualmente, es fácil ver que es un producto de la forma indicada para estar en . Finalmente, como
Definición. (Subgrupo Generado) Sean un grupo y un subconjunto de Decimos que un subgrupo de está generado por cuando . En tal caso, decimos que es un conjunto de generadores de
Ejemplos.
La siguiente proposición establece una caracterización de en términos de subgrupos de
Proposición 1. (Intersección de Subgrupos) Sean un grupo y un subconjunto de Sea la intersección de todos los subgrupos de que contienen a Entonces, .
-
Demostración: Realmente lo único que hay que probar es que es un subgrupo de Notemos que no es vacío, ya que el elemento neutro es elemento de cualquier subgrupo y, en particular, de aquellos que contienen a Sean x, y elementos de Entonces, dichos elementos estarán en cualquier subgrupo que contenga a (Lema 1). Para cada uno de esos subgrupos , tendremos que está en por lo que estará en la intersección de esos subgrupos. Lo que prueba que es un subgrupo. Por el lema 2, es un subgrupo de Pero como, es la intersección de todos los subgrupos que contienen a está contenido en Luego, .
El siguiente ejemplo muestra como usamos lo anterior para asegurar la existencia de un subgrupo, aunque no tengamos una idea precisa de cuales son sus elementos.
Ejemplo.(Subgrupo de los Conmutadores).
Sea un grupo. Llamamos conmutador de los elementos al elemento denotado por y definido por .
Llamamos subgrupo de los conmutadores o grupo derivado de al subgrupo generado por todos los conmutadores de Lo simbolizamos por .
El grupo Diedral
[editar]Llamamos grupo diedral de orden al grupo denotado por y definido como
Esto es, tiene dos generadores llamados y , sujetos a las restricciones indicadas.
Observemos que genera un subgrupo cíclico de orden y un subgrupo cíclico de orden 2. Luego, es el inverso de mientras que es su propio inverso. Al ser generado por los elementos son productos de . Por la observación anterior, esto se reduce a productos de potencias naturales de y .
donde los son positivos o cero. Observando que la tercera restricción, implica que vemos que cada vez que haya una delante de una , podremos aplicar la relación anterior y la pasa para detrás de Así, que consiste de los productos
Luego, tiene elementos diferentes.
Por ejemplo, supongamos que tenemos en ( ) los elementos , y Entonces, tenemos las siguientes simplificaciones.
De acuerdo a lo anterior, tenemos que,
Aplicando lo dicho arriba, tenemos la siguiente tabla para
Generadores del Grupo Lineal
[editar]En cursos básicos (también en curso de ÁLgebra Lineal) se estudia un procedimiento muy eficaz para la resolución de sistemas numéricos de ecuaciones lineales: el procidiemiento de Gauss-Joradan. Dicho procedimiento consiste de manipulaciones de las filas del sistema que permite (cuando hay solución única) diagonalizar el sistema.
Dichos procedimientos son equivalengtes a multiplicaciones por la izquierda con matrices especiales, llamadas matrices elementales . El procedimiento implica que cualquier matriz invertible, multiplicada de una secuencia de matgrices elementales produce la identidad. Como los inversos de matrices elementales son también elmentales, lo anterior implica que cualquier matriz invertible es igual a un producto de matrices elementales. Es decir que el grupo lineal está generado por las matrices elementales.
Los Generadores del Grupo Simétrico
[editar]En el capítulo anterior, vimos que cada permutación era un producto de ciclos, lo que el lenguaje de esta capítulo dice que los grupos simétricos son generados por ciclos. Veremos, a continuación, otros posibles conjuntos de generadores. Introduciremos la noción de signo de una permutación que ilustrará la eficiencia de disponer de buenos conjuntos de generadores y que nos servirá para introducir un importante subgrupo de el grupo alternante.
Descomposición en transposiciones
[editar]Sabemos que cada permutación puede expresarse como producto de ciclos disjuntos. Veremos, a continuación, como expresar un ciclo como producto de transposiciones y, posteriormente, como producto de una familia especial de transposiciones.
Proposición 2. Cada ciclo de largo es un producto de transposiciones.
-
Demostración: Si el resultado es trivial.
Supongamos el resultado cierto para todos los ciclos de largo inferior o igual a Sea y sea Entonces,
For Also, and Luego, es un ciclo de largo Por inducción,
Multiplicando en la derecha por obtenemos el resultado.
Corolario 1.1. El grupo simétrico es generado por sus transposiciones.
La cantidad de generadores de un grupo simétrico puede reducirse aún más si consideramos una familia especial de transposiciones.
Definición. (Transposición Simple) Llamamos transposiciones simples de a las transposiciones
Una noción que está asociada con las transposiciones es la noción de inversión.Definición. (Inversión) Sea en Una inversión de es un par tal que Simbolizaremos al conjunto formado por todas las inversiones de por y por a la cantidad de inversiones de
Ejemplo.
Sea
Se tiene las siguientes inversiones: (1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (3,4), por lo que
Ejemplo (Bubble Sort).
En muchas situaciones, necesitamos ordenar (respecto a algún criterio) una lista desordenada de objetos. En computación, hay un algoritmo llamado ordenamiento por la burbuja (en inglés, bubble sort) que se basa en el resultado anunciado. El algoritmo es fácil de recordar:
Suponer dada una lista
Ejemplo.
Ordenar la lista 632145 en orden ascendente.
A continuación, indicamos los pasos
Si pensamos la lista original como una permutación de 123456, tenemos que multiplicando por las transposiciones realizadas, obtendremos la identidad.
Luego, como las transposiciones son sus propios inversos, tenemos que
Notemos que aparecieron las transposiciones simples.
Lema A Sea en ssi, Si entonces hay un tal que
-
Demostración: Cuando se tiene que no hay inversiones de donde se tiene el resultado.
Supongamos que Si para todo se tiene que implica que Luego, implica que Si para Entonces implica que Por inducción, concluimos que Luego, hay tales que Sea el menor de tales enteros. Entonces, el par es una inversión. Lo que prueba que
Si se tiene que ; por lo que tenemos la segunda afirmación.
Lema B. Sea una transposición simple y sea en Entonces,
-
Demostración: Supongamos que Entonces,
Por lo que el par es una inversión de Sea una inversión de y consideremos el par Se debe tener que ya que la única inversión de es que como no es una inversión de no se puede tener que Entonces es una inversión de que no es igual a Por lo tanto, la correspondencia que a cada par de le asocia el par de es una función que probaremos que es biyectiva. En efecto, dicha función tiene inversa dada por por el mismo argumento usado arriba. Luego,
Suponer, ahora, que Entonces, Luego, por el resultado anterior. Despejando se obtiene lo anunciado.
Usaremos los lemas anteriores para probar la siguiente proposición.
Proposición 3. Sea en Entonces
-
Demostración: Usaremos inducción sobre para probar a). Si se tiene que que se puede considerar como el producto de un conjunto vacío de transposiciones. Cuando no es la identidad, por el lema A, hay un entero tal que Por lo que Por inducción, puede escribirse como el producto de transposiciones simples. Luego, es el producto de transposiciones simples. Lo que prueba la parte a).
Para probar la minimalidad de supongamos que es la cantidad menor necesaria de transposiciones. Sigue de lo anterior que Por inducción, sobre probaremos que Si el resultado sigue de la primera parte. Supongamos que Entonces, podremos hallar una transposición elemental tal que Por lo que por inducción y por el lema B, se tendrá que de donde el resultado.
El Signo de una Permutación
[editar]Sea Para cada en definamos
Notemos, que difiere de a lo más por el signo. Definamos por
Por lo tanto,
Ejemplo ( ).
Sea Entonces,
Luego,
Ejemplo ( ).
Sea la transposición Probaremos, formalmente que Organizaremos los factores de como en el ejemplo anterior. Primero aquellos donde luego aquellos con etc.
Veamos, el efecto de en y
Luego, Por lo que, \end{ejemplo}
Claramente, cada inversión produce un cambio de signo, por lo que De forma más general, cuando es una función cualquiera, tenemos que
Lema C.
- Demostración:
Proposición 4.
-
Demostración: Todas las transposiciones son conjugadas de Los --ciclos son productos de transposiciones. <
Nomenclatura. Diremos que una permutación es par cuando su signo sea igual a 1; en caso contrario diremos que es una permutación impar.
El Grupo Alternante
[editar]Definición. (Grupo Alternante) Llamamos grupo alternante de grado al núcleo del homomorfismo signo. Es decir al subgrupo de formado por todas las permutaciones pares. Notación:
Observaciones.
La siguiente proposición es un recíproco parcial de la última observación.
Proposición 5. Cada permutación de es un producto de 3-ciclos, cuando Es decir que los 3--ciclos generan al grupo
-
Demostración: Como cada permutación es el producto de una cantidad pares de transposiciones, bastara probar que el producto de dos transposiciones es siempre un 3--ciclo o un producto de 3--ciclos.
Ejercicios
[editar]Los Grupos de Simetrías
[editar]En esta sección, veremos algunos grupos que se presentan de forma natural cuando consideramos simetrías de figuras planas. Primeramente, precisaremos la nomenclatura que usa alremos. Nuestro universo es el plano, al que siempre consideraremos como el plano cartesiano .
Llamamos transformación del plano a cualquier función del plano en si mismo. Las transformaciones biyectivas son los elementos del grupo simétrico del plano. Estamos interesados en una familia de transformaciones especiales: Las congruencias, que son aquellas transformaciones biyectivas que preservan la distancia entre puntos. Es decir, que la distancia entre las imágenes de un par de puntos es igual a la distancia entre los puntos. Es fácil ver que todas las congruencias determinan un grupo de transformaciones del plano, llamado el grupo euclídeo} del plano y que denotaremos como .
En efecto, si y son congruencias, se tiene que
Lo que prueba que efectivamente es un grupo de transformaciones.
En textos de Geometría se prueba que las traslaciones, rotaciones y reflexiones son congruencias. Además, se verifica que las reflexiones generan el grupo Euclídeo. De hecho que cada congruencia es el producto de a lo más tres reflexiones. Ver [1] o [2]
Nomenclatura. Para las transformaciones de un conjunto cualquiera, tenemos la siguiente nomenclatura con respecto a su acción.
Sea una transformación de un conjunto
Una rotación siempre deja a su centro fijo. Una reflexión (del plano) entorno al eje deja fijo puntualmente el eje y globalmente, pero no puntualmente, al eje
Las Simetrías
[editar]Llamamos figura (plana) a un subconjunto cualquiera del plano. Algunos \newline ejemplos de figuras son las líneas, los cuadrados, las circunferencias, los sectores circulares, etc.
Decimos que una congruencia es una simetría de una figura </math> F</math> cuando la congruencia fija globalmente a la figura, o sea es tal que
Las simetrías de una figura forman un grupo, subgrupo del grupo Euclídeo, ya que (como es fácil verificar) la identidad es una simetría (de cualquier figura), la composición de dos simetrías de y la inversa de una simetrías de son simetrías. Usaremos la notación para las simetrías de
Las Simetrías del Cuadrado
[editar]Supongamos que tenemos un cuadrado hecho de un material rígido, donde por material rígido queremos decir que lo podemos manipular sin que se deforme. Supongamos, además, que:

Observemos que si rotamos por un cuarto de vuelta, el cuadrado quedará coincidiendo con su imagen en la superficie y que si no fuera por las etiquetas de los vértices, no nos daríamos cuenta del cambio. Esto es lo que quiere decir dejar fija globalmente a la figura. Llamemos a la rotación por un cuarto de vuelta.
Si volvemos a rotar por nuevamente llevaremos al cuadrado a coincidir con su imagen en la superficie. Simbolizaremos por la doble rotación, por la triple rotación, etc. Notemos que si efectuamos (cuatro cuartos de vuelta), volveremos a la posición original, por lo que si no hubiéramos visto el cambio, diríamos que nada ha pasado, que todo se encuentra idénticamente igual a la posición original. Por esa razón escribiremos que donde significa que las etiquetas en el cuadrado y en la superficie coinciden. Es decir que se trata de la identidad que fija todos los puntos de la figura.
En lenguaje de la teoría de grupos, tiene orden 4.
Es fácil ver que todas las posibles rotaciones distintas, que llevan al cuadrado sobre su imagen, son y y que aplicando consecutivamente dos de esas rotaciones, obtenemos una rotación de ese conjunto. Es decir que tenemos una operación en el conjunto de las rotaciones que corresponde a la composición de transformaciones (como funciones).
Como tenemos que las rotaciones determinan un grupo cíclico.
¿Habrá otros movimientos del cuadrado que lo lleven a cubrir su imagen en la superficie?
La respuesta es afirmativa, pero tendremos que sacar el alfiler que lo sujetaba a la superficie.Sea la reflexión entorno a la diagonal Es decir que envía en en y los puntos y quedan fijos. Notemos que Análogamente, tenemos la reflexión entorno a que envía en y en Hay dos reflexiones adicionales ( ) que introduciremos más tarde. La figura muestra las simetrías que son reflexiones del cuadrado, identificadas por su eje. Introduciremos, a continuación, una notación que nos servirá para identificar las simetrías del cuadrado con permutaciones de los vértices.

Observemos que las simetrías quedan totalmente identificadas cuando damos sus efectos en los vértices. Por ejemplo la rotación es tal que
Por lo que podemos identificar a las simetrías del cuadrado con permutaciones del conjunto de vértices. Usando esta identificación, tenemos que
De la misma manera, tenemos que las reflexiones introducidas tendrán como permutaciones a
Notemos que escribiendo las simetrías anteriores como ciclos, tenemos que
Usando la identificación resulta fácil computar los efectos de aplicar simetrías en forma consecutiva. Por ejemplo,
Es decir que se intercambian con y con Geométricamente, esta es la reflexión entorno a la línea que pasa por los puntos medios de los segmentos y Tendremos otra reflexión, entorno a un línea que pasa por los puntos medios de y es decir que
Computemos
Observemos que implica que
Sea el grupo generado por y Como tenemos las relaciones y vemos que coincide con el grupo diedral poniendo y
Interrogante ¿Habrá otras simetrías del cuadrado?Suponer que es una simetría del cuadrado diferente de la identidad.
Cuando un vértice queda fijo por el vértice opuesto también queda fijo, porque en caso contrario su imagen sería adyacente al vértice fijo y no permanecerían invariantes las distancias entre los vértices. Es decir que es o Este razonamiento prueba también que no hay 3--ciclos que puedan ser simetrías del cuadrado.
Cuando un conjunto de dos vértices queda globalmente fijo, pero no puntualmente fijo, hay una transposición de los dos vértices. Cuando los vértices son adyacentes, sus opuestos deben intercambiarse ( ). Si los vértices son opuestos, el otro par de vértices puede quedar fijo puntualmente o intercambiarse. Por lo que es una de las siguientes simetrías.
es decir y
Si una simetría diferente de la identidad deja fijo globalmente tres vértices, el cuarto vértice quedaría fijo; lo que vimos anteriormente que es imposible.
Finalmente consideremos el caso donde la simetría no tiene subconjuntos con dos elementos fijo globalmente. Por lo que se representa por un 4--ciclo.
Entonces, Si entonces ya que en caso contrario no se preservaría distancias. Luego, la imagen de es un vértice adyacente. El mismo razonamiento aplica a los otros vértices, por lo que concluimos que
o Como conclusión final tenemos la siguiente proposición.
Proposición 6. El grupo diedral contiene a todas las simetrías del cuadrado.
Representación Matricial de D8
[editar]Supongamos que estamos trabajando en el plano cartesiano Supongamos, además, que nuestro cuadrado tiene como vértices a y
Sean y
Es decir que generan un subgrupo de matrices isomorfo a
Ejercicios
[editar]Operaciones con Subconjuntos
[editar]Introduciremos una notación que nos ayudará en el enunciado de teoremas y que, también, será útil en consideraciones posteriores.
Definición. (Operaciones con Subconjuntos) Sea un grupo y sean A, subconjuntos de
Observaciones. Sea un grupo.
Ejemplo.
Sean y ¿Qué es ? Notemos la notación aditiva usada ya que la operación del grupo es suma.
-
Resolución. Como está formado por todos los múltiplos de 2 y por todos los múltiplos de 3, estará formado por todos los enteros que son iguales a la suma de un múltiplo de 2 con un múltiplo de 3.
Como Se tiene que
Advertencia.
Cuando y son subgrupos de el conjunto no es necesariamente un subgrupo de ya que si son elementos de no necesariamente se tiene que sea igual a un de
Ejemplo.
Sea Sean y Entonces, Notemos que, en este ejemplo, y son subgrupos de pero que no lo es (¿por qué no es subgrupo?).
Sea entonces
Ejercicios
[editar]
Subgrupo Generado por dos Subgrupos
[editar]En general, cuando y son subgrupos, el producto no es un subgrupo, por lo que el subgrupo que contenga a dos subgrupos debe definirse otra manera.
Definición. ( ) Sean y subgrupos de un grupo Por denotaremos al subgrupo generado por la (re)unión de y
Sea Claramente, y están contenidos en por lo que y son subgrupos de Sea cualquier subgrupo de que contenga a y a Entonces, contendrá cualquier producto de elementos de y por lo que contendrá a probando que es el menor subgrupo que contiene a y
Proposición 6. ( ) Sean subgrupos de Entonces, es el menor subgrupo (respecto a la inclusión) que contiene a ambos subgrupos.}}
Ejemplo.
Sea Sean y Entonces,
Diagrama de Subconjuntos El conjunto de subgrupos es un conjunto parcialmente ordenado por la inclusión. Dados subgrupos se tiene que
Es decir, que dos elementos tienen siempre un mayor elemento menor o igual que ellos y un menor elemento mayor o igual que ellos. Conjuntos parcialmente ordenados con esa propiedad se llaman Retículos.
Producto Directo de Subgrupos
[editar]Diremos que un grupo es el producto interno de dos subgrupos y cuando sea isomorfo al product
Proposición 7. (Producto Interno) Sea un grupo y sean subgrupos de es el producto interno de y ssi, se cumple que:
- Si está en y está en
- está generado por y
-
Demostración: ( ) Supongamos que hay un isomorfismo tal que Observemos que en es un subgrupo de cuya imagen por es Por lo que Análogamente, Observemos que si entonces está en y por lo debe ser igual a de donde Observando que tenemos la parte 2. La tercera parte sigue de que está generado por
( ) Sea tal que La conmutatividad de los elementos de con los elementos de implica que
Es decir que es un homomorfismo de grupos.
Si tenemos que es decir que h está en por lo que lo que implica que es inyectiva. Como generan a tenemos que los elementos de son productos de la forma
Por la conmutatividad de los elementos de con los elementos de tenemos que el producto anterior se puede reescribir con todos los adelante de los es decir de la forma hk con h en y k en K. Lo que muestra que es suprayectiva, probando que es un isomorfismo.
Ejercicios del Capítulo
[editar]- Hallar el centro y las clases de conjugación del grupo
- Sea el grupo cuya tabla se indica a continuación.
- Probar que
- Probar que es el grupo de las simetrías del hexágono regular. (Sugerencia: Suponga que los vértices del hexágono son en forma ordenada cíclica y Llamar a la rotación entorno al centro por grados. Llamar a la reflexión entorno a la línea que pasa por Probar que y que Representar y como permutaciones para efectuar las computaciones.)
- Hallar cada uno de los subgrupos indicados:
- Dibujar el diagrama de subgrupos de
- Hallar el centro y las clases de conjugación del grupo.
- Probar que Interpretar geométricamente el resultado.
- Sea Sean y Determinar los siguientes conjuntos
- Consideremos el grupo
- Probar que cada número entero puede escribirse como un múltiplo de 5 más un múltiplo de 3. Usar lo anterior, para concluir que
- Probar que
- ¿Cuándo, para un par de números enteros y se cumple que ?
- Sean y subgrupos de tales que Probar que cada elemento de tiene una única representación como con en y en (Sug. Suponer que ).
- Construir la tabla del grupo aditivo Sean math>H= [2],</math> Probar que de las dos maneras siguientes.
- Usando el teorema de la sección de productos.
- Mostrando que y
- Sea Hallar los subgrupos generados por los conjuntos indicados.
- Clasificar los enunciados siguientes en válidos o falsos.
- Todo grupo puede presentarse como un conjunto de generadores.
- Un grupo finitamente generado es finito.
- Cuando los generadores de un grupo permutan entre si, entonces el grupo es abeliano.
- Un grupo que es producto de otros dos es infinito.
- Los generadores de .
Verificar que las matrices elementales generan al grupo lineal.
Las matrices elementales son:donde es cualquier número real.
Hallar los inversos de cada una de las matrices elementales y observar que son también elementales.
Sea invertible. Por lo tanto, el determinante de , no es nu
- Suponer que . Entonces .
Probar que es una matriz diagonal. - Suponer y .Probar que es una matriz que tiene un cero en la posición (2,1).
- Suponer que (por lo que .) Probar que intercambia la primera fila con la segunda.
Los procedimientos anteriores muestran como podemos por multiplicación por matrices elementales obtener una matriz diagonal a partir de una matriz invertible cualquiera.
- Si en la posición (1,1) hay un elemento no nulo, usamos la matriz de intecambio (c) para obtener un elemento no nulo en la posición (1,1) del producto.
- Si en la posición (1,1) hay un elemento no nulo, aplicando el paso (b) obtenemos un elemento nulo en la posicion (2,3) del producto.
- Finalmente, si el elemento en la posición (1,2) no es nulo, aplicamo el paso (a) para obtener un producto con cero en la posición (1,2).
Nuestro producto es ahora una matriz diagonal. Observando que
completamos los productos necesario obtener la identidad.
- Suponer que . Entonces .
Comentarios
[editar]La determinación de los conjuntos generadores de un grupo tienen importancia teórica y práctica. Una rama especializada la teoría combinatoria de grupos, que estudia a los gruposgrupos desde el punto de vista de sus generadores y restricciones.
Un objeto muy interesante es el grupo libre sobre un conjunto que consiste de todos las palabras posibles con alfabeto . Se prueba que tofo grupo finito se obiene por restricciones de un rupo linreinitente generado.
Lectura adicïonal Wiipedia:Concepto generador de un grupo.
Notas
[editar]
9. Los Grupos Cocientes
[editar]10. Teoremas de Homomorfismos
[editar]Introducción
[editar]En este capítulo, veremos el teorema fundamental de homomorfismos, usualmente atribuido a Emmy Noether (1882-1935), que relaciona de una manera brillante los grupos cocientes con las imágenes homomórficas de un grupo. Aplicaremos dichos resultados para obtener unos resultados clásicos de la teoría de números.
Teorema Fundamental de Homomorfismos
[editar]Recordemos que cuando un homomorfismo es un supramorfismo, entonces decimos que es una imagen homomórfica de . El teorema fundamental establece una correspondencia biyectiva entre las imágenes homomórficas de y los subgrupos normales de .
Teorema de Fundamental de Homomorfismos (Teorema de Noether) [1]
Sea un homomorfismo de grupos y sea el núcleo de . Entonces,

El isomorfismo está dado por la correspondencia que a cada de asocia el elemento de .
-
Demostración: Primeramente, estableceremos que es una función bien definida, es decir que su valor es independiente del representante de la clase usado para computar su valor.
Sea en . Entonces, hay un en tal que . Luego,
Lo que prueba que está bien definida. Probaremos, ahora que se trata de un homomorfismo.
Claramente, es suprayectiva, por lo que basta verificar que es inyectiva, para concluir que se trata de un isomorfismo. Si se tiene que por lo que está en de donde el neutro de lo que prueba la inyectividad de .
Corolario.
- Demostración: Se tiene del isomorfismo anteriormente establecido que |f(G)|= |G/K|, donde K = ker(f). De donde, por el teorema de Lagrange obtendremos que |G| = |G/K||K|, lo que al sustituir en la relación anterior nos da el resultado deseado.
Notemos que el orden de la imagen de un homomorfismo es un divisor del orden del grupo.
Cómputo de Homomorfismos
[editar]Ejemplo.
Hallar todos los homomorfismos posibles desde en .
Resolución: Sea un homomorfismo. Entonces, implica que o . En el segundo caso, se trata de el neutro en . En el primer caso, se trata de un monomorfismo que envía el en un elemento de orden 5 en . ¿Cuáles son los elementos de orden 5 en ? La respuesta es 2, 4, 6, y 8. Por lo tanto, tenemos homomorfismos dados por donde a = 2, 4, 6 u 8.
Ejemplo.
Hallar todos los homomorfismos posibles desde en .
Resolución Sea el homomorfismo que envía el generador de en el generador de . Entonces, $\ker(f) \vartriangleleft \textsf{C}_{12}</math> implica que es un divisor de 12, o sea 1, 2, 3, 4, 6 o 12. Por el teorema acerca del orden de subgrupos de un grupo cíclico, tenemos que debe ser un divisor de 9. Lo que elimina a todos los valores de , excepto posiblemente o .
- corresponde al homomorfismo trivial (el neutro de ).
- implica que . La clase de tiene entonces orden 3, por lo que su imagen por debe tener orden 3. Sigue de la proposición mencionada que los únicos elementos de con orden 3, son y . Luego, los homomorfismos no triviales son tales que
- , o sea que , donde es el residuo de la división de por 3, y
- , o sea que , donde es el residuo de la división de por 3.
Ejercicios
[editar]- (Homomorfismos y ordenes) Sea un homomorfismo de grupos. Si entonces .
- Sea el grupo lineal (las matrices invertibles sobre los Reales). El subgrupo de formado por las matrices de determinante 1 es un subgrupo normal de . Describir a su grupo cociente.
- Sea un grupo. Para cada elemento de definamos la función (conjugación por ) de en sí mismo, por: .
- Probar que c_g es un isomorfismo de grupos.
- Si H es un subgrupo de G, entonces c_g(H) será también un subgrupo de G, llamado el conjugado de por c_g. Probar que es normal en ssi, coincide con todos sus conjugados.
- ¿Qué relación hay entre el diagrama de los subgrupos de un grupo y el correspondiente diagrama para un grupo cociente del mismo?
- (Isomorfismo de Productos)
- Sean y numeros enteros positivos relativamente primos entre si. Probar que el grupo es isomorfo a .
- Sean enteros positivos relativamente primos entre sí. Entonces,
donde .
- ¿Cuáles son todos los homomorfismos posibles de en y viceversa?
- Listar todos los posibles homomorfismos de en cuando r y s son iguales respectivamente a
(a) 4, 2. (b) 6, 2. (c) 6, 3. (d) 9, 3. - Listar todos los posibles homomorfismos de en
(a) r = 1, s = n. (b) r = 2, s = 3,4,5,n. (c) r = 4, s = 5,n. (d) r = 4, s = 6,9,n,2n. - Sea tal que .
- Probar que f es un homomorfismo de grupos.
- Probar que donde es el conjunto de todos los complejos cuyo módulo es igual a 1. Geométricamente, es la circunferencia unitaria del plano complejo.
- Hallar el núcleo de . (Se trata de un grupo muy conocido).
- Aplicar el teorema de Noether, para concluir que
- (Segundo Teorema de Isomorfismo) Sea un grupo y subgrupos normales de tales que . Probar las siguientes afirmaciones.
- implica .
- .
- La función tal que es un supramorfismo de grupos.
- El núcleo de consiste de todos las clase tales que está en o sea .
- (Segundo Teorema).
- (Tercer Teorema de Isomorfismo) Sea un grupo y subgrupos de tales que es normal en . Probar las siguientes afirmaciones.
- es un subgrupo de .
- es un subgrupo normal de .
- es un subgrupo de .
- es un subgrupo normal de .
- Sea la asignación a cada de de es un supramorfismo de grupos.
- El kernel de es .
- (Tercer Teorema).
Aplicaciones
[editar]Teorema Chino de los Residuos
[editar]Como una primera aplicación del teorema de Noether, probaremos el siguiente resultado.
Proposición 1. Si y son enteros relativamente primos entre si, se cumple que
-
Demostración: Sea tal que Como
tenemos que es un homomorfismo de grupos.
Computemos ahora el núcleo de Si entonces es divisible tanto por como por por ser y relativamente primos, tenemos que es divisible por por lo que pertenece a Observemos, además, que cualquier elemento de es divisible tanto por como por por lo que su imagen por será precisamente Es decir que el núcleo de es
Luego, por el teorema de Noether, Es decir, Pero, como concluimos que por lo que
La proposición anterior tiene el siguiente corolario, que aparece en la literatura matemática como el teorema Chino de los Residuos.
Corolario 1.1. Sean ... , numeros enteros relativamente primos entre si. Sea igual al producto de esos números. Entonces,
por un isomorfismo tal que
-
Demostración: Inducción sobre
Hay un teorema de igual nombre en teoría de números que enunciamos a continuación.
Corolario (Teorema Chino de los Residuos para los Números Enteros) Sean \dots, números enteros relativamente primos entre si y sea el producto de esos números. El sistema de congruencias
tiene una solución entera. Dos de esas soluciones son congruentes módulo
-
Demostración: Sea el isomorfismo del corolario anterior. La solución a la congruencia es cualquier tal que
La función de Euler
[editar]Recordemos que es la cantidad de enteros positivos menores o iguales que que son relativamente primos con Sabemos que las clases de congruencia de esos números determinan al grupo multiplicativo En esta sección, probaremos un resultado que permitirá computar para cualquier valor entero de Necesitaremos el resultado de la siguiente proposición.
Proposición 2. Sean y dos enteros positivos relativamente primos. Entonces,
-
Demostración: Consideremos el grupo y sean y los subgrupos definidos por
y
Probaremos que Se tiene que y son normales en porque es un grupo abeliano. Si y tenemos que es divisible por y lo que implica, por ser y relativamente primos, que es divisible por o sea que Es decir que Para probar lo anunciado, solamente nos falta probar que está generado por y Como y son relativamente primos, hay enteros tales que
Sean y Observemos que está en y que está en Además,
Lo que prueba que Por la proposición sobre el producto de subgrupos normales, tenemos que
Probaremos ahora que y que lo que concluirá la demostración de la proposición.
Observemos que si es relativamente primo con se cumple que es relativamente primo con Por lo que la correspondencia induce una función Claramente, esta función es un homomorfismo. Si en es tal que se debe cumplir que y Sigue del teorema Chino de los Residuos, que hay un único elemento con esa propiedad, 1. Por lo que es un monomorfismo. Para probar que es suprayectiva, para cada en debemos poder hallar un entero en tal que Es decir un entero tal que y Nuevamente, por el teorema Chino de los Residuos, tal existe, Luego es un isomorfismo de en
De manera análoga, se verifica que Luego,
Contando los elementos en la relación de la proposición anterior, tenemos el siguiente resultado.
Proposición 3. Sean m</math> y enteros positivos relativamente primos. Entonces, se cumple que {Eqn| }}
Una función de los Enteros en los Enteros con la propiedad anterior, se dice que es
Veremos como la proposición anterior, junto con la fórmula para potencias de primos
permite computar para todo número natural
Proposición 4. Sea n</math> un número entero positivo mayor que 1. Si la descomposición en factores primos de es
entonces,
-
Demostración: Aplicar la proposición anterior e inducción.
Ejemplo.
Hallar
Como
Ejemplo
[editar]- Hallar enteros tales que
Los Grupos Simples
[editar]Los grupos simples son una familia muy importante de grupos.
Definición. (Grupo Simple) Decimos que un grupo es simple cuando no contiene subgrupos propios no nulos que sean normales.
Sigue del teorema de Noether que cuando es simple y es un homomorfismo, entonces es el homomorfismo trivial o es un isomorfismo sobre su imagen.
Sea cualquier grupo finito abeliano. Recordemos que cualquier subgrupo de es normal en Sea un elemento no nulo de y sea Si entonces el grupo es cíclico y tiene subgrupos para cada divisor positivo de por lo que será simple, ssi, es primo. Si entonces es un subgrupo propio de y, por lo tanto, normal en
Proposición 5.
Los grupos finitos abelianos simples son los cíclicos de orden primo.
Sea G un grupo finito cualquiera. Cuando G no sea simple, deberá tener un subgrupo normal propio. Seleccionemos un subgrupo N normal maximal. Es decir tal que no haya un subgrupo normal H distinto de N y G, que contenga a N. En tal situación, tenemos el siguiente lema.
Lema. Sea un grupo finito cualquiera y sea un subgrupo normal maximal de Entonces, es simple.
-
Demostración: Sea el supramorfismo canónico, Supongamos que no fuera simple. Entonces, habría un subgrupo normal propio de digamos Sea la imagen inversa de es decir que
Sabemos que es un subgrupo de Probaremos que contiene propiamente a que está contenido propiamente en y que es normal en G, lo que contradice la maximalidad de
Como es un subgrupo propio de se tiene que es decir que hay un en que es diferente de o sea tal que es diferente de lo que implica que es un elemento de que no está en Análogamente, como hay un que no está en por lo que no está en Luego, es un subgrupo propio de que contiene propiamente a Veamos. ahora, por qué es normal en Sea un elemento cualquiera de y un elemento de Entonces, como es normal en tenemos que es un elemento de lo que implica que esta en o sea que
Series de Composición
[editar]Sea un grupo finito cualquiera. Veremos, ahora, como generar una cadena finita de subgrupos de
| (**) |
tal que cada es un subgrupo normal maximal de
Sea un subgrupo normal maximal de Si es simple, En caso contrario, seleccionar un que sea normal y maximal. Repitamos el proceso anterior, usando como grupo inicial a obteniendo un subgrupo que sea normal maximal en Repetir el proceso hasta que el subgrupo maximal normal sea Como cada subgrupo obtenido está propiamente contenido en el subgrupo anterior, el proceso anterior tiene una cantidad finita de pasos.
En la cadena (**) de subgrupos, se tiene que es simple. La sucesión
se llama una serie de composición para
Se puede probar que, seleccionando cualquier subgrupo maximal inicial como (pueden haber varios) que la serie de composición es esencialmente la misma, excepto por una permutación de los grupos cocientes que allí aparecen (teorema de Jordan-Holder). Es decir que la serie solamente depende del grupo G, por lo que grupos isomórficos tienen esencialmente la misma serie. En ese sentido, los grupos simples son los bloques básicos para los grupos finitos generales.
Una de las tareas importantes realizadas por los matemáticos en el siglo XX, fue la construcción de un catálogo de los grupos finitos simples. La tarea envolvió a matemáticos de diferentes países y épocas. Finalmente, en 1982 se estimó que se había completado el catálogo. La demostración de los elementos del catálogo así como de su completitud ocupa varios miles de páginas, distribuidas en centenares de artículos. Una tarea, todavía en proceso (2011), es la reescritura unificada de tal demostración.
Hay otros tipos de series, por ejemplo requiriendo que los cocientes sean abelianos (no necesariamente simples), que caracterizan a familias de grupos.
Ejercicios del Capítulo
[editar]- Sea un grupo y sea el subgrupo de los conmutadores, que es el subgrupo generado por los conmutadores de o sea, los elementos de la forma Probar o hacer lo indicado.
- es un grupo abeliano.
- Si y es abeliano, entonces contiene a
- Hallar el grupo de conmutadores de y
- Sea un grupo cuyos únicos subgrupos son los triviales: y Probar que es finito y su orden es un número primo.
- Un grupo que contiene un subgrupo de orden 2 no es simple.
- Sea todas las matrices invertibles con entradas que son elementos de Hallar todas las matrices de ese conjunto y verificar que determinan un grupo. Hallar un grupo conocido isomorfo a ese grupo.
- Sean y subgrupos normales de un grupo Probar las siguientes afirmaciones.
- Si y entonces
- Sea un grupo de orden con impar. Probar que tiene exactamente un elemento de orden 2, Además que el producto de todos los elementos del grupo es precisamente ese elemento de orden 2.
- La siguiente afirmación es una proposición de la teoría de números enteros que se pueden probar aplicando la teoría de grupos a los grupos para un adecuado. (Wilson) Si es un primo, }.
- Sea un grupo y sea el subgrupo de los conmutadores, que es el subgrupo generado por los conmutadores de o sea, los elementos de la forma Probar o hacer lo indicado.
- es un grupo abeliano.
- Si y es abeliano, entonces contiene a
- Hallar el grupo de conmutadores de y
- Sea un grupo de orden donde es un primo impar. Probar que es el grupo cíclico o el grupo dihedral
- Clasificar cada una de las siguientes afirmaciones como válidas o falsas. Cuando sea válida dar una explicación o demostración de su validez. En caso contrario, proveer un contraejemplo.
- Todo grupo contiene un subgrupo propio cíclico.
- Cuando el conjunto de generadores de un grupo es finito, entonces el grupo es finito.
- Si el orden de es para todo divisor de hay un elemento de de orden
- Si el orden de es para todo divisor primo de hay un elemento de de orden
- En un grupo de orden todos los elementos no nulo tienen orden
- Hay grupos de orden donde para todo en se cumple que para un entero positivo
- La imagen homomórfica de un grupo cíclico es un grupo cíclico.
- La imagen homomórfica de un grupo infinito es siempre un grupo infinito.
- Un subgrupo es normal, ssi, coincide con todos sus conjugados.
- Un grupo de orden 121 contiene un elemento de orden 11.
- Un grupo de orden 100 tiene un subgrupo de orden 4, pero no un subgrupo de orden 8.
- Un subgrupo de orden 256 contiene un subgrupo de orden 16.
- (Variación del Teorema de Noether) Sea un homomorfismo de grupos. Sean la suprayección canónica, tal que y la función definida por la inclusión. se puede factorizar como
- Verificar que se puede factorizar como Comparar esa factorización con la factorización de funciones del apéndice Las Funciones.
- Probar que las funciones en la factorización son homomorfismos de grupos.
- Sea un monoide. Sea un submonoide de (o sea un subconjunto cerrado de que contiene al neutro).
- Definir clases laterales e Probar que la relación ssi, es un relación de equivalencia en Denotaremos por al conjunto formado por todas las clases de equivalencia.
- Suponer que es tal que para todo en Probar que es una operación bien definida en que provee a con una estructura de monoide tal que la función de en es un homomorfismo suprayectivo de monoides.
- Enunciar un teorema análogo al teorema de Noether para los homomorfismo de monoides.
Comentarios
[editar]Teoremas de Isomorfismos. El teorema de Noether es llamado el primer teorema de isomorfismos porque hay al menos otros dos. No parece haber acuerdo acerca de cuál de ellos es el segundo y cuál es el tercero. Ver enunciados de esos teoremas en los ejercicios de la sección Teorema Fundamental de Homomorfismos Ver también Wikipedia:Teoremas de Isomorfía
Notas
[editar]- ↑ Algunas veces, en la literatura matemática, se llama al teorema, "el primer teorema de homomorfismos". Ver los comentarios.
11. Clasificación de Grupos
[editar]Introducción
[editar]Clasificar familias de grupos significa, hallar todos los posibles tipos (no isomorfos) de los grupos de la familia. En este capítulo, veremos la clasificación por orden de grupos finitos.
Sea un grupo con . Sabemos que:
- cuando n es un número primo, es cíclico
- hay un único grupo de orden n, cuando n=1,2,3 y que
- para cada n, hay al menos un grupo de orden n, el grupo cíclico de ese orden
Clasificación de los Grupos de Orden 4
[editar]Sea un grupo de orden 4, que no sea cíclico. Como no es cíclico, todos los elementos diferentes del neutro deben tener orden 2. Por lo que tiene tres subgrupos de orden 2, , donde
Sea .- Si z=e, se tiene que ab = e, lo que implica que aab=a, o sea que b= a. Imposible.
- Si z=a o z=b se concluye, respectivamente que b=e o que a =e. Imposible.
que . Por simetría entre a y b, concluimos que, también, ba=c. Por lo tanto, si existe un grupo no cíclico de orden 4, debería ser
Claramente, este grupo existe, es nuestro viejo conocido: el
grupo de Klein.
Un grupo de orden 4 es isomorfo a:
- el grupo cíclico de orden 4, o
- el grupo de Klein.
La Cardinalidad del Producto de dos Subgrupos
[editar]Antes de continuar nuestros estudios de clasificación, probaremos un resultado acerca de la cardinalidad del conjunto producto de dos subgrupos, que nos ayudará en clasificaciones futuras.
Recordemos que el conjunto producto de dos subgrupos no necesariamente determina un subgrupo. Sean y subgrupos de , ¿cuántos elementos tiene ? Suponiendo y . tendremos que todos los productos que podemos tomar con primer factor en y segundo en serán . Sin embargo, algunos de esos productos podrían ser iguales entre si. Es decir que podemos afirmar que:
Proposición 1 (Cardinalidad de un Conjunto Producto de Subgrupos)
Sean y subgrupos de .
Entonces,Clasificación de los grupos de orden 6
[editar]Aplicaremos los resultados anteriores a la clasificación de los grupos de orden 6. Clasificar significa, hallar todos los posibles tipos (no isomorfos) de una familia de grupos, en este caso de los grupos cuyo orden es 6.
Sea un grupo de orden 6. Como, para cada posible orden tenemos un grupo cíclico de orden 6, nos podemos preguntar ¿aparte del cíclico cuántos (tipos de) grupos diferentes de orden 6 hay? Nosotros conocemos al menos uno adicional, .
Supongamos que no fuera cíclico. Por el teorema de Lagrange, sabemos que los únicos ordenes posibles para los subgrupos y, por lo tanto, para los elementos son 1, 2, 3 y 6.
El neutro es el único elemento de orden .
Si hubiera un elemento con orden 6, el grupo sería cíclico. Lo que nos deja como posibles ordenes para subgrupos 2 y 3, por lo que esos subgrupos necesariamente tienen que ser cíclicos.
Supongamos que todos los elementos diferentes del neutro tuvieran orden 2. En tal caso, como . sigue que para todo . Además, implicará que , o sea que el grupo sería abeliano. Sean y dos de esos elementos de orden . Entonces, sería un subgrupo de . Por la conmutatividad, consistiría exactamente de los productos de la forma . o sea, . Pero esto es imposible, ya que no puede haber un subgrupo de orden 4 en un grupo de orden 6. Conclusión: no todos los elementos pueden tener orden 2; lo cual implica que debe haber al menos un elemento de orden 3, digamos .
Como tiene orden 3, el subgrupo también tiene orden 3, lo que implica y son elementos con orden 3. ¿Habrá algún otro subgrupo de orden ? Supongamos que sí y que se tratara de . Como este subgrupo sería distinto de , tendríamos que . Por lo tanto, calculando la cantidad de elementos del producto , tendríamos que
tanto, hay solamente un subgrupo de orden y todos los elementos restantes, diferentes del neutro, deberán tener orden 2.
Sea uno de ellos, entonces la clase lateral derecha tendrá tres elementos y, por ser disjunta con , coincide con el complemento de . por lo que contendrá a todos los elementos de orden 2. Se tiene así que
estructura de . bastará con conocer el producto de .
- Si entonces, es el inverso de y tendría su mismo orden, lo que no puede ser.
- Si entonces . imposible.
- Si entonces, . imposible.
- Si . entonces . imposible.
- Si . el grupo sería abeliano y el elemento tendría orden 6, por lo que el grupo sería cíclico; imposible.
- Por lo tanto la única posibilidad es que
Los razonamientos anteriores muestran que la única posibilidad de grupo de orden 6, aparte del cíclico, será entonces . Resumiendo tenemos lo siguiente:
- el grupo cíclico de orden 6, o
- el grupo . caracterizado como .
Clasificación de los Grupos Abelianos de orden 8
[editar]Sea un grupo abeliano tal que . Si hay un elemento en cuyo orden sea igual a , se tiene que es un grupo cíclico de orden 8.
Supongamos que no es cíclico. Entonces, todos los elementos no nulos deben tener ordenes 2 o 4.
Suponer que de tiene orden y sea el subgrupo generado por . Supongamos que haya otro elemento de orden 4, digamos tal que no está en . Sea . Si , por el teorema de la cardinalidad de productos, tenemos que
Lo que es imposible, luego . Entonces, o 4. No puede ser 4, porque entonces . Por lo que .
De donde sigue que o sea que . ¿Qué elementos hay comunes en la intersección? Observemos que , por lo que . Observemos que entonces, es un elemento que no está en , porque implica que estaría en . Se tiene que , por lo que hay un elemento de con orden 2. Sea . Entonces , y o sea que . Sigue entonces, de la proposición acerca del producto de subgrupos normales, que .
Si fuera de todos los elementos tuvieran orden 2. Escogiendo, uno cualesquiera de ellos, podríamos repetir el argumento anterior. Supongamos que todos los elementos no nulos tuvieran orden 2. Seleccionando tres de ellos, digamos, , y , tendríamos que
- un grupo cíclico de orden 8, o
- el producto de un grupo cíclico de orden 4 con uno de orden 2, o
- el producto de tres grupos cíclicos de orden 2 cada uno.
Clasificación de los Grupos de orden 9
[editar]Sea un grupo cuyo orden es . Si tiene un elemento de orden 9, es el grupo cíclico de orden 9, . En caso contrario, todos los elementos diferentes del neutro deben tener orden 3. Sean y dos subgrupos diferentes generados por elementos de orden 3. Se tiene que , por lo que . Es decir que . Primeramente, probaremos que es normal en . Es decir que, para todo en se cumple que es un elemento de . El típico elemento de es
| (*) |
Observando que vemos que basta verificar que
está en .
Se tiene que
| (**) |
para tales que . Queremos probar, que
necesariamente . Recordemos, que como los elementos
diferentes del neutro son de orden 3, tenemos que
. Además, y , ya que, en caso contrario, tendríamos que
- Si , entonces (**) implica que lo que implica que , lo que no puede ser. Luego, .
- . Esto dice que . Esto dice que o que , y ambas posibilidades son contradictorias a las elecciones de y .
- implica que , o sea que .
- , lo que sabemos que es contradictorio.
- . Una contradicción.
Como todos los casos con conducen a contradicción, debemos concluir que . Lo que prueba que es normal en .
Por la simetría de la situación, tenemos que es, también, normal en . Por la proposición \ref{propInternoNormales}, tenemos que .
Es decir que cualquier grupo con 9 elementos es el grupo cíclico de 9 elementos, , o el producto de dos grupos cíclicos de orden 3 cada uno. Resumiendo,
|
|
conmutativos de orden 9.
Caracterización de los Grupos Cíclicos Finitos
[editar]Sabemos que cada elemento de un grupo finito tiene un orden que es un divisor del orden del grupo. Introduciremos la noción de exponente de un grupo que nos ayudará en la caracterización de los grupos cíclicos finitos.
Definición. (Exponente de un Grupo) Sea un grupo finito. Llamamos exponente del grupo al menor entero positivo tal que para todo elemento dell grupo. Lo denotaremos por .
Por ejemplo, , .
Como , tenemos que es un
múltiplo de .
Un grupo cíclico es un grupo tal que . El objetivo de esta sección es mostrar que esa relación caracteriza a los grupos cíclicos entre los grupos finitos abelianos.
Necesitaremos el siguiente lema que provee una caracterización para el exponente.
Lema. Sea un grupo finito abeliano y sea un elemento cuyo orden es maximal entre los ordenes de los elementos de . Entonces, .
-
Demostración: Debemos probar que para todo en . Supongamos que tenemos descomposiciones en factores primos de y dadas por
donde los 's son primos diferentes entre si y los exponentes 's, 's son mayores o iguales que cero.
Si , se tendría que habría un , sin perdida de generalidad, podemos suponer que . Sean , , y . Entonces, tenemos que y . Se tiene entonces que el máximo común divisor de y es 1, por lo que . Pero esto contradice la maximalidad de .
Proposición 2. (Caracterización de Grupos Cíclicos) Sea un grupo finito abeliano. Entonces, es cíclico, ssi, .
-
Demostración: Si , entonces
. Recíprocamente, supongamos que
; entonces hay un elemento tal que
, por lo que es cíclico.
Ejercicios del Capítulo
[editar]- Probar que el producto de dos grupos abelianos es un grupo abeliano.
- Sea un grupo abeliano tal que donde y son números primos diferentes. Probar que hay elementos , tales que , y que .
- Clasificar los grupos de orden 10, 14 y 15.
12. Teoremas de Cardinalidad
[editar]Introducción
[editar]Los teoremas de cardinalidad son aquellos teoremas que establecen relaciones referentes a cantidad de elementos o subgrupos con una cierta propiedad. Con anterioridad, hemos visto dos instancias de este clase de resultados: el teorema de Lagrange y el teorema acerca de la cardinalidad del conjunto producto de dos subgrupos. Los resultados principales que veremos en este capítulo serán la ecuación de clases--una relación acerca de la clases de conjugación, el teorema de Cauchy estableciendo la existencia de elementos de cierto orden y el (primer) teorema de Sylow estableciendo la existencia de subgrupos de cierto orden.
La Ecuación de Clases
[editar]Vimos, anteriormente, que la relación de conjugación es una relación de equivalencia en un grupo, por lo que particiona al grupo en clases disjuntas de equivalencias, llamadas clases de conjugación del grupo. La clase de conjugación de un elemento , denotada , está formada por todos los elementos conjugados a , es decir que
donde . Sea un conjunto de representantes de las clases de conjugación, es decir que consiste de un elemento de cada una de las clases de conjugación. Dos elementos diferentes de corresponden a dos clases diferentes. Como la reunión de las clases de conjugación es todo y como las clases son disjuntas, tenemos que la cantidad de elementos de es igual a la suma de los elementos en cada clase, o sea que
| (*) |
Nos referiremos a esa relación como la ecuación de las clases de conjugación. del grupo .
Hay una variación de la ecuación de clases de conjugación que resultará muy útil para futuros resultados, basada en que la cardinalidad de cada clase de equivalencia es igual al índice de un cierto subgrupo. Empezaremos nuestro trabajo introduciendo la noción de centralizador de un elemento.
Definición. (Centralizador) Sea un grupo y un elemento de . Llamamos centralizador en de al subconjunto de denotado por , o ---cuando queremos mencionar el grupo---y que está definido como
Observemos que esta en , ssi, , ssi, , ssi, . Es decir que los elementos del centralizador de son aquellos tales que el conjugado por de es igual a . Por lo que es un elemento de su centralizador.
Proposición 1. El centralizador de un elemento de un grupo es un subgrupo del grupo.
-
Demostración: Sea un grupo y el centralizador de en . El elemento neutro, claramente, está en .
Sean , elementos de . Tenemos que
, lo que muestras que es cerrado respecto a la operación del grupo. Además,
Lo que concluye la demostración.
Nos interesa considerar el conjunto cociente (que, en general, no será un grupo, pues no siempre es normal). Sean y tales que está en la coclase , es decir para algún en . Entonces,
Es decir que dos elementos de la misma coclase respecto a producen el mismo conjugado de .
Veamos el resultado recíproco. Sean , tales que . Como,
Por lo que está en , o sea que .
Por lo que, elementos de diferentes clases de conjugación de corresponden a diferentes coclases respecto a . Es decir que tenemos el siguiente resultado.
Proposición 2. Sea un grupo y un elemento del grupo. La cantidad de conjugados de es igual a la cantidad de coclases del centralizador de , o sea al índice .
Corolario 2.1. El cardinal de una clase de conjugación es un divisor del orden del grupo.
Usaremos el resultado de la proposición para reescribir la ecuación de clases de conjugación vista arriba. Recordemos que cada elemento del centro de un grupo () es el único elemento de su clase de conjugación. Por lo que usando el resultado de la proposición anterior, y reagrupando todos los elementos del centro tendremos que la ecuación de las clases de conjugación del grupo puede presentarse como sigue. (Donde es un conjunto de representantes de las clases de conjugación.)
|
|
Llamamos a esta ecuación, la ecuación de clases del grupo .
Algunos autores llaman ecuación de clases a lo que arriba hemos denominado ecuación de clases de conjugación.
Otra demosración de esta ecuación se puede obtener mediante la teoría de G-conjuntos que estudiaremos en el próximo capítulo.
Proposición 3. Sea un --grupo, es decir un grupo cuyo orden es una potencia de , primo. Entonces, el centro de no es trivial.
-
Demostración: Probaremos que .
Como es un --grupo, tenemos que cualquier elemento o subgrupo de tiene un orden que es una potencia de . Igualmente, el índice de cualquier subgrupo es una potencia de . En particular, para cualquier elemento de tenemos que es una potencia de . Consideremos la ecuación de clases
Tenemos que divide a y a cada sumando en la sumatoria, por lo tanto, divide el orden de .
Corolario 3.1. Un grupo cuyo orden es , primo, es un grupo abeliano.
-
Demostración: Sabemos por la proposición que , o .
- Si entonces y . Sigue de la proposición \ref{prop090404} que es abeliano.
- Si entonces , por lo que es abeliano.
Teoremas de Cauchy y Sylow
[editar]Anteriormente, afirmamos que no siempre era cierto que para cada divisor del orden de un grupo haya un subgrupo que tenga como orden ese divisor (ver ejemplo más adelante). Sin embargo, por el lado positivo tenemos dos importantes resultados, el teorema de Cauchy [1] y el (primer) teorema de Sylow [2].
Teorema. (Cauchy) Sea un factor primo del orden de un grupo. Entonces, hay al menos un subgrupo de orden en .
Teorema. (Primer teorema de Sylow) Sea un factor primo del orden de un grupo y sea , , un divisor del orden del grupo. Entonces, hay al menos un subgrupo de orden en .
Definición. (--Sylow subgrupo) Sea un grupo y un número primo.
Llamamos --Sylow subgrupo de al subgrupo de orden . tal que es la máxima potencia de que divide el orden de .
Notemos que del teorema de Sylow sigue la existencia de un --Sylow subgrupo de cualquier grupo con un divisor del orden de . Cuando , el subgrupo trivial es el --Sylow subgrupo de .
Como aplicaciones de los teoremas anteriores tendríamos, por ejemplo, las siguientes afirmaciones.
- Un grupo de orden 6 tiene al menos un grupo de orden 3 y uno de orden 2.
- Un grupo de orden 12 tiene subgrupos de orden 2, 3 y 4.
- Un grupo de orden 15 tiene subgrupos de orden 3 y 5.
-
(Demostración del teorema de Cauchy)
(Caso Abeliano.) Sea un grupo abeliano cuyo orden es divisible por el primo . Sabemos por ejemplos anteriores, que el resultado de la proposición es válido cuando . Razonando por inducción, supondremos el resultado válido para grupos de orden inferior a . Sea un elemento del grupo con . Si tenemos que es un elemento con orden . Supongamos, entonces, que y consideremos el subgrupo que tiene orden que es por el teorema de Lagrange un divisor de . Como , no puede ser igual a por lo que es un divisor propio de , y lo mismo pasa con el índice . Luego, . Como , pero , tenemos que . Como , aplicando la hipótesis de inducción, tenemos que hay un elemento de orden en . Sea tal que , entonces implica que es un elemento de , digamos que . Sea , como , tenemos que . Entonces,
En consecuencia, tenemos que es igual a 1 o a . Si , se tendría que . Como el orden de es , lo anterior,implicaría que , lo que es imposible, luego, el orden de es . Lo que acaba la demostración del caso abeliano.
(Caso no abeliano.) Sea un grupo no abeliano tal que el orden de es divisible por . Sabemos que el resultado es válido para , el menor grupo no abeliano es . Supongamos el resultado válido para todos los grupos con orden inferior a . Consideremos la ecuación de clases de ,
Si divide el orden de alguno de los , por inducción, este subgrupo propio de contendrá un elemento de orden , que será un elemento de orden de .
En caso contrario, como divide al orden de , será un factor de , para todo en . Como divide a , sigue de la ecuación de clases que divide el orden de , Como es abeliano, sigue del caso anterior, que hay un elemento de orden en y, por lo tanto, en .
-
(Demostración del teorema de Sylow.) Sea un grupo con orden donde es primo y . La demostración será por inducción sobre el orden del grupo. Sigue de los ejemplos, que el teorema es válido para grupos con ordenes pequeños. Analicemos la ecuación de clase para el grupo
Supongamos que no divide uno de los índices que aparecen en la ecuación. Entonces, debe dividir el orden de que, por no estar en el centro del grupo, es un subgrupo propio de . Se tiene, entonces, por inducción, que contiene un subgrupo de orden , por lo que contiene un subgrupo de orden .
En caso contrario, se tiene que divide el orden del centro. Sea cualquier elemento de orden en (que siempre hay por el teorema de Cauchy) y consideremos al grupo cociente , cuyo orden es . Nuevamente, por inducción, tenemos al existencia de un subgrupo de de orden , Sea la preimagen de por el supramorfismo canónico que envía cada elemento de en su coclase respecto a . es un subgrupo de y su orden es .
Observación. Hablamos de primer teorema de Sylow, porque hay otros que teoremas que establecen entre otras cosas que todos los --Sylow subgrupos (puede haber varios) son conjugados entre sí, que la cantidad de tales subgrupos es un divisor del orden del grupo, que dicha cantidad es congruente con 1 módulo y que cada subgrupo de orden una potencia de está contenido en exactamente un --Sylow subgrupo. Tales resultados son muy útiles para la clasificación de subgrupos finitos. Sin embargo, exceden los propósitos de este texto. Ver los comentarios al final del capítulo.
Ejemplo
[editar]El ejemplo de esta sección nos servirá para ilustrar que la relación de ser subgrupo normal no es transitiva y que puede haber grupos tales que no hay un subgrupo cuyo orden sea un divisor dado del grupo.

Rotaciones del tetraedro regular.
Consideremos al tetraedro regular con vértices llamados 1, 2, 3 y 4. Consideraremos, inicialmente, rotaciones por 120 grados alrededor de un eje que pasa por uno de los vértices y el centro de la cara opuesta, Dichas rotaciones fijan uno de los vértices y permutan los otros tres, por lo que las indicaremos como permutaciones de , es decir permutaciones de .
SeanSea . Notemos que cada una de las rotaciones anteriores tiene orden 3. Además son distintas entre si, al igual que sus cuadrados (notar que dejan fijo un vértice distinto). Notemos que el conjunto producto de y tiene 9 elementos. Por lo que el orden de será 12 o 24---los únicos divisores de 24 mayores o iguales a 9. Notemos que la permutación de no puede pertenecer a ya que representa una transformación imposible para un tetraedro rígido. Por lo que .
Notemos que sigue del razonamiento anterior que cualquier par de esas rotaciones genera a todo el grupo. Sean , y . Entonces, todos ellos son elementos de orden 2, ya que
- .
- .
Aplicando el teorema de Sylow a cuyo orden 12 es igual a vemos que debe tener subgrupos de ordenes , y . Subgrupos de orden son obviamente , y . El --Sylow subgrupo de tiene cuatro elementos, por lo que no puede contener ninguna de las rotaciones, por lo que debe ser . Notemos que como cada elemento de es su propio inverso, por lo que es isomorfo al grupo de Klein. Observemos que , por lo que .
Todos los elementos fuera de tienen orden 3, por lo que los conjugados de elementos de serán elementos de y es por lo tanto normal en . Hay cuatro 3--Sylow subgrupos: , , y . Se puede verificar que ninguno de ellos es normal en .
Usaremos el grupo para ilustrar dos situaciones interesantes. Sea . Como se tiene que es un subgrupo de y, en consecuencia, de . Como subgrupo de es normal en , ya que es abeliano. Computando un conjugado,
vemos que no es normal en . Es decir que la relación de ser normal no es transitiva.
Se tiene que 6 es un divisor del orden de . ¿Hay algún subgrupo de orden 6 en ? Supongamos que fuera un subgrupo de orden 6 de . Entonces, debe contener un elemento de orden 3 y uno de orden 2. Observemos que solamente puede contener uno de los , , y por que un subgrupo conteniendo 2 de ellos es igual a . Análogamente, solamente uno de los elementos de orden 2 están en ese grupo, ya que dos de ellos generan un subgrupo de orden 4. Supongamos que fuera el elemento de orden 2. Si está en , está en y , l que no puede ser. Si está en tenemos que estaría en , pero , lo que es imposible. Si está en , también lo estaría , imposible. Finalmente, si estuviera en , también estaría , lo que, nuevamente, es imposible. Repitiendo lo anterior con y , se ve que es imposible la existencia de un subgrupo con 6 elementos.
Ejercicios del Capítulo
[editar]- Sea un grupo abeliano y sean y elementos de tales que el orden de es y el orden de es . Probar que el orden de es igual al mínimo común múltiplo de y . (Probar que si es un múltiplo común de y , entonces ).
- Probar que los grupos abelianos de orden 16 son , , , y .
- Listar todos los subgrupos de .
- Clasificar los grupos abelianos de orden 27.
- Sea un grupo abeliano tal que donde y son números primos diferentes. Probar que hay elementos , tales que y y .
- Analizar las estructuras posibles para un grupo de orden 8. (Sug: Hay cinco posibles; tres abelianos y dos no abelianas).
- Clasificar los grupos de orden 25.
- Sea .
- Probar que es un grupo de orden 12.
- Probar que es isomorfo al grupo de las simetrías del tetraedro.
- Sea un grupo cuyo orden es , primo, . Probar, sin usar el teorema de Cauchy, que tiene un elemento de orden . (Sugerencia: probar las siguientes afirmaciones.) \begin{enumerate}
- Si es cíclico entonces tiene un elemento de orden .
- Si es abeliano entonces contiene un elemento de orden . (Considerar cualquiera de sus subgrupos cíclicos).
- Si no es abeliano, probar que su centro tiene un orden divisible por , por lo que contiene un elemento de orden . (Usar la ecuación de clases.)
Comentarios
[editar]Teoremas de Sylow. Hablamos de primer teorema de Sylow, porque hay
otros dos teoremas que enunciaremos a continuación. La demostración se puede ver en el Apéndice "Teoremas de Sylow".Segundo teorema de Sylow. Sea un grupo. Dos -grupos de Sylow cualesquiera son conjugados. Además, cualquier -subgrupo (subgrupo cuyo orden es una potencia de p) está contenido en un -Sylow subgrupo.
Tercer teorema de Sylow. Sea un grupo tal que donde es un primo que no divide a . Sea el conjunto de todos los -Sylow subgrupos de . Entonces,
- es un divisor de m,
- .
Los teoremas de Sylow están entre los resultados más importantes en la teoría general de grupos finitos. Las demostraciones aparecen en el Apéndice Teoremas de Sylow.
Muchos otros detalles y demostraciones se pueden hallar en [3]
Notas
[editar]13. Las Acciones de Grupos
[editar]Introducción
[editar]Las acciones de un grupo cualquiera sobre un cierto conjunto son generalizaciones de dos importantes acciones:
- la acción del grupo simétrico sobre los elementos de mediante permutación de sus elementos, y
- la acción del grupo lineal sobre los puntos del espacio -dimensional mediante la multiplicación de una matriz por un vector.
G-conjuntos
[editar]Definición. (G-Conjunto) Sean un grupo y un conjunto no vacío. Decimos que actúa en cuando hay una función
tal que, simbolizando a la imagen por de la pareja se cumpla que:
En tal situación, decimos que: es una acción de sobre o, también, que es un G-conjunto.
Ejemplos.
- Sea un conjunto no vacío. El grupo simétrico actúa de manera natural sobre mediante la acción definida por
- La acción de asocia a cada matriz del grupo y punto el punto (multiplicación de matriz por vector).
- Cada grupo actúa sobre si mismo mediante la acción definida por la operación del grupo.
- (Acción por la izquierda)
- (Acción por la derecha)
- Sea un grupo. Otra acción de en si mismo mediante es provista por la conjugación. Para cada en recordemos que llamamos conjugación por a la función de en si mismo, tal que
Es fácil verificar que la función
define una acción de sobre si mismo. \fin
- Sea un grupo y un subgrupo de Entonces actúa en mediante la acción definida por:
Observación. Asociado a -conjuntos, tenemos la noción de -subconjunto. Un subconjunto de un -conjunto es un -subconjunto, ssi, para todo en en está en . También, decimos que es G-invariante.
Definición. (G-morfismo) Sean dos -conjuntos. Decimos que una función es un -morfismo, ssi, permuta con la acción. Es decir, ssi,
- Claramente, la identidad es un -morfismo y la composición de dos -morfismos es un - morfismo.
- Cuando no haya riesgo de confusión, de ahora en adelante, podremos escribir simplemente en lugar de
- La terminología de mono, supra, endo, auto se extiende a -morfismos con el significado obvio.
Como se cumple que se tiene que cada función es invertible. Es decir que podemos definir de manera natural una función
que asigna a cada en la función en Las suposiciones sobre la acción implican que esa función es un homomorfismo de grupos. De forma recíproca, cuando sea un homomorfismo cualquiera de grupos, podemos definir una acción de en por:
Es decir que hay una correspondencia, que se puede probar que es biyectiva, entre acciones de sobre y las representaciones (homomorfismos) de en (Representación permutacional del grupo.)
La última correspondencia nos dice también que si es un -conjunto y hay un homomorfismo de grupos es también un - conjunto, vía la composición de homomorfismos.
En particular, cuando sea una subgrupo de cada - conjunto tendrá una estructura de -conjunto, vía la inclusión, a la que llamaremos la restricción de la acción de G a H.
Definición. (Órbita, Grupo de isotropía) Sean un -conjunto y un elemento de
- Llamamos órbita de por al subconjunto de formado por todos los elementos de de la forma Notación:
- Cuando sólo haya una órbita para la acción del grupo, decimos que el grupo actúa transitivamente, o también que el -conjunto es transitivo.
- Decimos que un elemento de fija a cuando
- Llamamos grupo de isotropía o estabilizador de al subconjunto de formado por todos los elementos de que fijan a
Es fácil verificar que es un subgrupo de (de ahí el nombre de grupo). En efecto, no es vacío, ya que contiene al neutro. Si y están en se tiene que:
Ejemplos.
- El grupo actúa en de manera transitiva, ya que dados elementos la transposición toma uno en el otro. Por lo tanto, todos los elementos de pertenecen a la misma orbita.
- El grupo simétrico en elementos puede considerarse actuando en , por la acción natural sobre Coincide así con el subgrupo de formado por las permutaciones que dejan a fijo. Es decir, que podemos identificar el grupo simétrico con el (sub)grupo de isotropía de en %
- Sea el subgrupo de generado por actúa en fijando y y permutando y Por lo tanto, tendremos tres órbitas: y
- La acción (izquierda o derecha) de una grupo en si mismo definida por la operación es una acción transitiva. Es decir que hay una única órbita para la acción que es igual a todo el grupo.
- En la acción por conjugación, la órbita de es la clase de conjugación de y el grupo de isotropía de es el centralizador de
- El grupo de isotropía de por la acción natural de en consiste de todos los en tales que Es decir de todos los en Es decir, el grupo de isotropía de coincide con Claramente, la acción de es transitiva sobre
La siguiente proposición es de fácil verificación:
Proposición 1. Sea un -morfismo. Entonces, el grupo de isotropía de está contenido en el grupo de isotropía de Además, dichos grupos coincidirán, cuando sea inyectiva.
Sean un -conjunto, elementos de y un elemento en las órbitas de y Entonces, podremos hallar en tales que Por lo que, lo que implica que está en la órbita de y viceversa. Por lo tanto, las órbitas o son iguales o no se intersecan. Es decir, las órbitas de la acción de definen una partición de En otras palabras:
Proposición 2. Sea un -conjunto. Si definimos la relación por ssi, para algún en se tiene que: es una relación de equivalencia cuyas clases de equivalencia coinciden con las órbitas de en
Sea un -grupo y sea un elemento de
Sea definida por Como tendremos que es una -morfismo, cuya imagen es precisamente la órbita de Notemos que es equivalente a afirmar que Es decir, que Esto, a su vez, implica que las clases de equivalencia de coinciden con las clases laterales izquierdas de respecto a En particular, esto nos dice que hay una biyección entre y Tal biyección es un G-morfismo, o sea que como G-conjuntos son isomórficos.
Sea un subgrupo cualquiera de entonces es de forma natural un -conjunto. Supongamos que hubiera una -morfismo de en tal que Entonces, como el grupo de isotropía de estaría contenido en el grupo de isotropía de tendríamos que sería un subgrupo de En forma recíproca, si es un subgrupo de podemos definir por
La función estará bien definida, ya que si se tendría que Además y Es decir, es un -morfismo. Es decir, que hemos probado la siguiente proposición.
Proposición 3. Sea un -conjunto, un subgrupo de y un -mor\-fismo de en tal que ssi, Dicha aplicación es un -isomorfismo cuando Es decir, como -conjuntos son isomorfos y (la órbita de ).
Corolario 3.1. Sea un grupo finito que actúa en el conjunto finito Entonces,
Las órbitas de en el -conjunto determinan una partición de Llamaremos conjunto de representantes de las órbitas, a un subconjunto de que contiene exactamente un elemento de cada una de las órbitas.
Corolario 3.2. (Conteo para -conjuntos) Sea un -conjunto finito. Entonces,
Donde es un conjunto de representantes de las órbitas.
Ejercicios
[editar]- Sea un grupo tal que con primo.
- Cada clase de conjugación de tiene como cardinal una potencia de
- Considere el conjunto formado por todos los elementos cuya clase de conjugación consiste de un sólo elemento. Probar que dicho conjunto no es vacío.
- Usando el hecho que:
donde los denotan a las distintas clases de conjugación de concluir que hay elementos diferentes del neutro que tienen clases de conjugación consistentes de un único elemento. ¿Cuál es el número mínimo de esos elementos?
- El centro de un grupo consiste de todos aquellos elementos que permutan con todos los elementos del grupo.
- Probar que el centro de un grupo es un subgrupo del grupo.
- Probar que la clase de conjugación de cada elemento del centro consiste únicamente del elemento. Usar esto para probar que el centro es un subgrupo normal de G.
- Probar que el centro de un -grupo (un grupo cuyo orden es una potencia de primo) es no trivial.
-
- La intersección de una familia de -conjuntos es un -conjunto, cuando dicha intersección no es vacía.
- Sea un -conjunto, un subconjunto no vacío de Probar que hay un -subconjunto de minimal conteniendo a al que simbolizaremos por y llamaremos el -subconjunto generado por
- El -subconjunto generado por un conjunto no vacío consiste de todas las órbitas de elementos de
- Sea el subgrupo de generado por y Considérese la acción natural izquierda de en ¿Cuáles son las órbitas de cada elemento? ¿Cuáles son sus grupos de isotropía?
- Sean dos -conjuntos. Definir una estructura de -conjunto en de modo que las proyecciones sean -morfismos.
- Sea un conjunto, el producto cartesiano de copias de Para en definir
Probar que la definición anterior define una acción de en
Los Grupos Geométricos
[editar]El apéndice Los Grupos Geométricos contiene definiciones, nociones y teoremas relacionados con la Geometría. En particular, de los grupos asociados a las nociones geométricas.
En esta sección veremos algunas de las acciones de los grupos geométricos del plano.
Acción de las Traslaciones
[editar]Sea P un punto (vector plano) cualquiera del plano y C un vector fijo. La traslación por es la transformación biyectiva . Luego, es fijo por , ssi, , ssi, . Notemos que una traslación deja fijo un punto, ssi, es la traslación por el vector nulo, ssi, . Luego, si una traslación fija un punto, fija a todos los puntos.
Las traslaciones determinan el subgrupo de transformaciones (ver el apéndice citado).
Notemos que dados puntos y del plano, poniendo , tenemos que . Es decir que para la acción deel grupo de las traslaciones, el plano tiene una única órbita, lo que equivale a afirmar que el grupo de las traslaciones actúa transitivamente en el plano.
Acción de las Transformaciones Lineales
[editar]El grupo es el grupo de las matrices invertibles 2x2 (equivalentes a las transformaciones lineales invertibles). Cuando , su acción sobre un punto (representado por una matrix columna) es la multiplicación de matrices. Es decir,
Se verifica (ver apéndice Los Grupos Geométricos) que cuando es un elemento de , envía líneas sobre líneas y preserva el paralelismo (si dos líneas son paralelas, sus imágenes también lo son).
Las rotaciones alrededor del origen forma un grupo que simbolizaremos aquí por , se verifica que tales rotaciones son lineales con matriz dada por
donde es el ángulo de la rotación.
Un cómputo algebraico prueba que si es un rotación alrededor del origen, el único punto fijo por es el origen. Cuando , se tiene que la orbita de es la circunferencia con centro en el origen y radio la distancia de al origen.
Clasificación de las Congruencias
[editar]Ilustraremos la importancia de la noción de punto fijo, clasificando a las congruencias, es decir haciendo un listado de todas las posibles congruencias del plano.
Usaremos el siguiente resultado de la Geometría (ver apéndice citado arriba).
Proposición 4. Los puntos equidistantes a dos puntos dados forman una línea que es perpendicular a la linea que pasa por los puntos y corta a esa línea en el punto medio entre los puntos.
Llamamos simetral ortogonal de los puntos a la línea de la proposición.
Notemos que dada una línea la reflexión entorno a esa línea, fija cada punto de la línea, y envía cada punto que no está en la línea en un punto tal que la línea es la simetral ortogonal de y .
Sea una congruencia del plano.
- Si tiene tres puntos no colineales fijos entonces ; es decir deja a todos los puntos fijos.
Supongamos que , y son los tres puntos fijos. Supongamos que , es decir supongamos que hay un punto tal que . Sea fijo por , o sea . Entonces,
. Lo que dice que equidista de y , por lo que está en la simetral ortogonal de esos puntos. Como esto implica que , y son colineales (están en la misma línea), hemos llegado a una contradicción. Por lo que debe ser la identidad.
- Si tiene dos puntos fijos, es la identidad o una reflexión entorno a la línea que pasa por esos dos puntos.
Sean y los puntos fijos. Supongamos que no es la identidad. Entonces, debe haber un punto que no es colineal con y , tal que . Sea la reflexión en la simetral ortogonal de y . Entonces, razonando, como en el caso anterior, tenemos que y están en , por lo que son fijas por . Tenemos entonces, que
por lo que es una congruencia que fija tres puntos no colineales. del caso anterior, tenemos que , de donde, , de donde . - Si tiene un único punto fijo, entonces es un producto de dos reflexiones cuyos ejes se cortan en el punto fijo.
Sea el punto fijo. Entonces, para todo , . Razonando como arriba, pertenece a la simetral ortogonal a y . Sea la reflexión entorno a esa simetral. Entonces,
Por lo tanto, es una congruencia que deja dos puntos fijos, Por lo que es una reflexión, digamos que . Luego, (multiplicando por en ambos lados, tenemos que %f = \sigma sigma_1 </math>.
- Si no tiene puntos fijos, es el producto de tres reflexiones. Sea un punto cualquiera y sea la reflexión entorno a la simetral ortogonal de y . Entonces, , lo que prueba que tiene un punto fijo, por lo que es un producto de dos reflexiones, digamos . Procediendo, como arriba, se tiene que .
Los razonamientos anteriores prueban el siguiente teorema.
Teorema de Cartan--Dieudonné Cada congruencia del plano es el producto de a lo más tres reflexiones.
Notemos que los cómputos anteriores muestran que las rotaciones son producto de dos reflexiones cuyos ejes se cortan. Se puede probar que el producto de dos reflexiones cuyos ejes son paralelos es una traslación.
Ejercicios
[editar]- Sea un punto del plano. Verificar que las congruencias que fijan al punto forman un grupo de transformaciones
- Sea un punto del plano. Probar que las rotaciones alrededor de forman un grupo . Sea y sea una rotación alrededor del origen, o sea un elemento de .
- Probar que es una rotación alrededor de .
- Probar que y son subgrupos conjugados del grupo de transformaciones del plano.
- Una simetría central con centro en un punto es una transformación que envía cada punto en un punto .
- Probar que (punto medio entre y su imagen.
- Probar que las líneas que pasan por quedan fijas globalmente por .
- Probar que y que , es una traslación.
- Probar que el producto de una traslación por una simetría central es una simetría central.
- Si es el origen, es lineal. Hallar la correspondiente matriz.
Representación Lineal de Grupos
[editar]|
Esta sección requiere un conocimiento de nociones básicas de Álgebra Lineal. |
El objetivo de la sección es ver como podemos obtener para cualquier grupo, un grupo de matrices isomorfo. Podemos considerarlo tanto como una generalización o una concretization del teorema de Cayley por grupos de permutaciones, dependiendo de la familiaridad con el Álgebra Lineal. La teoría de las representaciones lineales iniciadas a fines del siglo XIX por Frobenius [4]. ha sido, es y continuará siendo un área activa, ya que permite un muy buen entendimiento de los grupos.
Sea un espacio vectorial de dimensión . Lo que significa que hay una base de vectores en , es decir un conjunto tal que cada vector de puede escribirse de una única manera como
Cada transformación lineal de en si mismo, tiene asociada una matriz, cuyas columnas son las coordenadas de las imágenes de los vectores de la base. Las transformaciones lineales biyectivas (isomorfismos lineales) tiene asociadas matrices invertibles, que determinan un grupo, el grupo lineal de ,
Definición. (Representación Lineal) Sea un espacio vectorial sobre un cuerpo cualquiera . Sea un grupo. Una representación de en es un homomorfismo de grupos
Tal homomorfismo define una acción de en por
Cada grupo tiene varias representaciones lineales posibles, qu aunque no siempre e pueden determinar el grupo, usualmente proveen valiosa información sobre el mismo. A nosotros nos interesara una representación en particular: la representación regular, que definiremos a continuación.
Sea . Asociaremos con el grupo un espacio vectorial sobre un cuerpo (que puede ser los Reales, los Complejos u otro cualquiera) denotado por y formado por todas las expresiones
Se define una suma y una multiplicación por escalares de modo que es una base de , es decir si y , entonces
Además, podemos definir una multiplicación en usando la multiplicación del grupo
donde es la multiplicación del grupo. Esta multiplicación provee a con una estructura de álgebra (anillo con operaciones compatibles con la multiplicación por escalar.
Para cada en la multiplicación produce una transformación lineal de . Además, es decir que tenemos una representación del grupo por las matrices de la forma . Es fácil verifica que la correspondencia es inyectiva. Esdecir que es isomorfo a un grupo de matrices, subgrupo de del grupo de isomorfismos lineales de .
La matriz de cada tiene una forma peculiar. En efecto, como su efecto en la base es una multiplicación por la izquierda en es una permutación de . Luego, la matriz
Como es un elemento de digamos que , la --ésima columna de , correspondiente a las coordenadas de , tiene un 0 en cada posición, excepto en la --ésima fila donde aparece un 1. (En otras palabras, las matrices tienen como columnas permutaciones de las columnas de la matrix identidad.
Ejemplo.
Sea . Entonces,
Tenemos el siguiente teorema.
Teorema. Cada grupo finito es isomorfo a un grupo de matrices.
Ejercicios
[editar]- Hallar el grupo de matrices correspondientes a la representación regular del grupo de Klein y aquella de
- Sea .
Probar que la asignación
define una representación de .
Comentarios
[editar]En el apéndice F,Teoremas de Sylow, se demuestran el segundo y tercer teorema de Sylow, usando técnicas de acción de grupos.
Notas
[editar]
C. Los Anillos
[editar]14. Los Anillos
[editar]15. Los Ideales y Anillos Cocientes
[editar]16. La Divisibilidad y los Dominios
[editar]Introducción
[editar]En este capítulo, estudiaremos abstracciones de la teoría de la divisibilidad de los Enteros. Aunque muchas de las nociones relevantes pueden extenderse a anillos cualesquiera, la extensión natural es a dominios de integridad (o sea anillos conmutativos con unidad y sin divisores de cero). En este capítulo, y en los siguientes, dominio será sinónimo de dominio de integridad.
Los Enteros están contenidos en los Racionales, que son un cuerpo formado por las fracciones de números enteros. En total analogía, veremos que cada dominio tiene asociado un cuerpo de fracciones de elementos del dominio.
Convenio. Todos nuestros anillos serán conmutativos con identidad, a menos se diga explícitamente lo contrario.
La Divisibilidad
[editar]En primer lugar, extenderemos la divisibilidad y nociones asociadas de los Enteros a anillos conmutativos generales.
Definición. (Divisores, Unidades, Asociados) Sea un anillo conmutativo con identidad.
- Decimos que un elemento no nulo divide a ssi, hay un elemento tal que Simbólicamente
- Decimos que un elemento de es una unidad, ssi, es un divisor de la identidad.
- Decimos que los elementos y son asociados, ssi, hay una unidad tal que
- Cuando divide a podemos también decir alguna de las siguientes expresiones.
- es un factor de
- des un divisor de
- es un múltiplo de
- es divisible por
- Las unidades ya habían sido definidas anteriormente como los elementos invertibles del dominio. Claramente, ambas nociones coinciden.
- Un divisor de cero es cualquier elemento no nulo que divide (en el sentido de la definición) al 0, o que es un factor no nulo del 0.
La siguiente proposición resume las principales propiedades de la divisibilidad.
Proposición 1. Sea un anillo conmutativo con identidad. Para todo en se cumple que
- Cualquier elemento es divisible por 1,
- Cualquier elemento es divisible por sí mismo,
- Cero es divisible por cualquier elemento,
- La relación de divisibilidad es transitiva. Es decir, si y entonces
- Si y entonces
- Si entonces
-
Demostración: Ejercicio.
Unidades
[editar]Como observamos anteriormente, la noción de unidad en un anillo es lo mismo que invertible respecto a la multiplicación, pero la tradición es usar el nombre unidad en el contexto de divisibilidad.
Observemos que cuando es una unidad, como es un divisor de cualquier elemento del anillo. Claramente, en cualquier anillo, y son divisores de 1 y son, por lo tanto, unidades. El siguiente ejemplo muestra que, en general, puede haber otras unidades en un anillo. Además, en cualquier cuerpo, cualquier elemento no nulo es una unidad.
Ejemplo (Enteros de Gauss).
Sea Sabemos de ejemplos anteriores que es un anillo respecto a las operaciones usuales. Además, como es un subconjunto de es un dominio de integridad.
Además de y también son unidades y ya que Se puede verificar que esas son las únicas unidades de ese anillo.
Simbolizamos el conjunto de las unidades de un anillo por o Como las unidades son los elementos invertibles, es cerrado respecto a la multiplicación, contiene al 1 y es cerrado respecto a tomar inversos. Es decir que tiene una estructura de grupo, que es un subgrupo del semigrupo multiplicativo del anillo.
Asociados
[editar]Sea un asociado de , digamos que donde es una unidad. Sea tal que Entonces,
lo que prueba que está asociado con Es decir que la relación "estar asociado con" es una relación simétrica. De hecho, puede probarse que es una relación de equivalencia.
La siguiente proposición es básica para entender el rol de las unidades en la divisibilidad y las nociones asociadas con ella.
Proposición 2. Sea un anillo conmutativo con Identidad. Sean y elementos de tales que
- Cualquier asociado de divide a
- Cualquier asociado de es divisible por
-
Demostración: Supongamos que es tal
Sea con unidad. Entonces, lo que prueba que divide a
Sea con unidad. Entonces, lo que prueba que divide a
Los resultados de la proposición muestran los roles de las unidades en un anillo, y los problemas que ocasionan. Supongamos que queremos definir máximo común divisor (MCD) de dos elementos de un anillo. Nos gustaría tener una definición que leyera como sigue:
- Sean y dos elementos de un anillo (conmutativo con identidad). Un elemento es un MCD de y ssi,
- es un divisor común de y y
- es divisible por cualquier otro divisor común.
Esta definición tiene dos variaciones con respecto a la definición usual para los enteros. En la definición para números enteros se pide que el MCD sea un número positivo. Como en general, no tenemos orden, no podemos hablar de elementos positivos. Sigue de la definición, que si hay un MCD de dos números, por la proposición anterior, cualquier asociado con él, también será un MCD. Por eso es que hablamos de un MCD y no de el MCD.
Ejemplo.
En los Enteros, de acuerdo a la definición anterior de se tiene que 4 y 6 tiene como MCD a 2 y a (el asociado a 2).
La consecuencia de lo anterior es que cualquier definición que use divisibilidad, por ejemplo, elemento primo, no determinará un único elemento, sino que al elemento y a todos sus asociados. Por lo que algunas veces hablaremos de unicidad, excepto por asociados o modulo asociados.
En el caso de los Enteros como y son los únicos asociados con podemos, usando el orden, escoger el positivo.
Algunos elementos importantes en un anillo conmutativo son los elementos irreducibles y los elementos primos, que definiremos a continuación. En el anillo de los Enteros, los números primos tienen dos propiedades básicas:
- (Irreducibilidad). Cada número primo es divisible solamente por si mismo (o un asociado) o por una unidad.
- (Primacidad) Cuando un número primo divide al producto de dos números, divide al menos a uno de ellos.
Generalizaremos esas dos nociones para anillos conmutativos cualesquiera como nociones separadas, ya que en general no coincidirán.
Definición. (Elementos Irreducibles, Primos) Sea un anillo conmutativo con identidad.
- Un elemento de es irreducible (en ), ssi, no es nulo ni es una unidad y implica que o es una unidad.
- Un elemento de es primo (en ), ssi, no es nulo, no es una unidad y cuando entonces o
Claramente, los asociados de irreducibles son irreducibles y los asociados de elementos primos son primos. La definición dice que un irreducible solamente tiene como factores a un asociado con él o a una unidad.
Observaciones.
- En el anillo de los números enteros, los números primos son irreducibles y primos de acuerdo a las definiciones anteriores.
- En un cuerpo, no hay elementos irreducibles ni primos, ya que todos los elementos no nulos son unidades. Desde el punto de vista de la divisibilidad, los cuerpos son triviales.
- Puede haber dominios donde haya elementos irreducibles que no son primos. Ver ejemplo más adelante.
La Aritmética en un Dominio
[editar]La divisibilidad puede definirse sobre cualquier anillo con identidad, tomando precauciones acerca del lado adonde estamos multiplicando. Para los efectos de nuestro estudio, sin embargo, las propiedades más interesantes se presentan cuando trabajamos sobre un dominio de integridad. La divisibilidad en un dominio tiene las siguientes propiedades adicionales.
Proposición 3. Sea un dominio, entonces
- Si y entonces y son asociados.
- Si hay un único elemento tal que Escribiremos que
- Demostración:
- Como hay un tal que Análogamente, implica que hay un tal que Luego, como se tiene que cancelando se tiene que por lo que y son unidades. De donde el resultado.
- Si por cancelación
Proposición 4. (Primos son Irreducibles)
Si es un elemento primo de un dominio es irreducible.
- Demostración: Sea un elemento primo de Supongamos que Luego, por definición de elemento primos se tiene que o Luego para o digamos se cumple que y que Por lo que, por la proposición anterior, se tiene que y son asociados. Luego hay una unidad tal que Como por cancelación se tiene que o sea que es una unidad.
Ejemplo (Un dominio donde hay un irreducible que no es primo).
Sea Sabemos que es un dominio, ya que es un subanillo de
Primeramente, determinaremos las unidades de Para en recordemos que llamamos norma de al número denotado por y definido como donde es el conjugado de como número complejo. Observemos que, en este caso, para cada en se cumple que Por lo que la norma de un elemento de es un número entero. Se cumple, además, que
Supongamos que fuera una unidad de Se tendría, entonces, que hay un tal que Por lo que Como los valores de la norma son enteros positivos o cero, tenemos que la norma de una unidad debe ser igual a 1. Luego, cuando es una unidad, tenemos que por lo que se cumplirá que y Luego, y son las únicas unidades de
Probaremos ahora que es irreducible. Suponiendo que tomando conjugados tenemos que Multiplicando las relaciones anteriores, obtenemos que
Luego es igual a 1 o 3 o 9. Como es imposible con entero y implica que la alternativa es imposible. Luego o Claramente, implica lo que dice que es un unidad. Si no es unidad, pero entonces por que una unidad. En consecuencia, 3 es irreducible.
Observemos ahora que Como, obviamente no divide a o a su conjugado, no puede ser primo.
Máximo Común Divisor y Mínimo Común Múltiplo
[editar]Las definiciones de los conceptos son totalmente análogas a los correspondientes conceptos para con los números enteros, excepto que no hay unicidad.
Definición. (MCD, MCM) Sea un dominio y sean elementos de y al menos uno de ellos no es nulo.
- Un elemento es un mcd (máximo común divisor) de y ssi, es un divisor común de y y es divisible por cualquier otro factor común. Notación
- Un elemento es un mcm (mínimo común múltiplo) de y ssi, es un múltiplo común de y y divide a cualquier otro múltiplo común. Notación
Observaciones.
- Cuando existen, dos mcd (resp. mcm) son asociados. Por lo que, cuando existen mcds, hay tantos mcd (resp. mcm) como unidades.
- Es posible tener dominios donde haya mcd, pero no mcm.
Se tiene la siguiente proposición.
Proposición 5. Sea un dominio y sean elementos no nulos de
- Si y tienen mcd y mcm, entonces, excepto por un asociado, se cumple que
- Si existe entonces
-
Demostración: Ejercicio.
- Probar la proposición 1.
- Sean elementos de un anillo Sea tal que y Probar que para todo en
- Sean una familia de elementos de un anillo y un divisor común de los elementos de la familia. Probar que divide cualquier combinación lineal de los 's con coeficientes en o sea que es un divisor de
para todo 's en - Probar que si y son elementos de un dominio de integridad y entonces
- Probar la proposición 5.
- Sea donde es un entero positivo. Probar que si es una unidad, entonces su conjugado también lo es.
- Sea el dominio de los Enteros de Gauss.
- Probar que es un factor de de y de
- Hallar otros tres factores de 2 en
- Sea un entero primo y sea Probar que es un dominio de integridad. Hallar las unidades y primos de Probar que cada primo en es irreducible.
- Sea Sea Construir la tabla de la adición y multiplicación de Hallar ideales de
- Sea y sea Verificar que;
- ssi, y
- es una unidad, ssi,
- y son unidades de
- es una unidad.
- es asociado de
- (¿Qué pasa con la factorización única?)
- Sea y sea
- Si están en
- La ecuación no tiene soluciones enteras.
- No hay elemento de tal que
- Un entero no nulo divide a ssi, divide a y a
- Hallar los ideales maximales y primos de
- Hallar los ideales maximales y primos de
- Hallar un ideal primo de que no sea maximal.
- Hallar un ideal primo de que no sea maximal.
- Hallar un ideal propio de que no sea primo.
- ¿Cierto o falso?
- Cada ideal primo de un anillo (conmutativo con identidad) es un ideal maximal.
- Cada ideal maximal de un anillo (conmutativo con identidad) es un ideal primo.
- La intersección de dos ideales primos es un ideal primo.
- Sea un entero primo y sea
- Probar que es un subanillo de pero no es un subcuerpo de
- Hallar las unidades de
- Probar que todos los ideales de son principales y de la forma
- Describir
- Dar un ejemplo de un anillo donde hay un ideal primo que no es maximal.
- Probar la proposición 9. .
- Probar que cada elemento de que no es unidad es nilpotente (tiene una potencia igual a cero).
- Verificar que es un cuerpo.
- Verificar que no es un cuerpo.
- ¿Cuáles son todos los ideales de cualquiera? (Sug. Probar que si es un ideal entonces es un ideal de que contiene a ) Aplicar lo anterior para hallar todos los ideales de Buscar los ideales primos y maximales entre ellos.
- Probar que cada ideal primo de un anillo finito (conmutativo con identidad) es maximal.
- Probar que un ideal en un anillo es maximal, ssi, es simple (no tiene ideales propios).
- Sean ideales de un anillo y sea un ideal primo de Probar que implica que o
- Reflexividad. Como se tiene que
- Simetría. Supongamos que de donde Es decir,
- Transitividad. Supongamos que y Entonces, se cumple que
Multiplicando término a término de las ecuaciones anteriores, obtenemos:
Es decir, de donde cancelando en ambos lados, obtendremos que Lo que es equivalente a afirmar que
- es un semigrupo con identidad, cuyos
elementos no nulos son todos invertibles.
Iniciaremos la demostración con la prueba de la asociatividad.
Usaremos la notación empleada en la demostración de la
asociatividad de la suma.
lo que prueba la asociatividad.
La conmutatividad sigue directamente de la definición.
Como concluimos que es una identidad.
Como ssi, Sigue que cuando se tiene que y por lo tanto, que es un elemento de Además se cumple que
Es decir que cada elemento no nulo tiene inverso multiplicativo.
(Distributividad.) Notación como en las pruebas de asociatividad.
lo que prueba la distributividad. - Completar la demostración de la proposición 11.
- Probar que el cuerpo de fracciones de
es
Determinar cuáles de los siguientes números están en En caso afirmativo expresarlos en la forma y racionales.
- Sea entero que no es un cuadrado perfecto. Probar que es un dominio y describir a su cuerpo de fracciones.
- Probar que los Racionales son el cuerpo de fracciones de los Enteros.
- Probar que no hay un número racional tal que (Suponer que lo hay, y usar que 2 es primo en el anillo )
- ¿Cuál es el cuerpo de fracciones de un cuerpo?
- Sean elementos de un dominio. Probar que ssi, y son asociados.
- Probar que la relación de "ser asociado con" es una relación de equivalencia.
- Sea el dominio de los enteros de Gauss y sea la norma de .
- Probar que 5 no es irreducible en Sugerencia por lo que no puede ser un elemento primo de
- Probar que 3 es irreducible en
- Probar que un número entero primo que puede escribirse como la suma de dos cuadrados, digamos no puede ser irreducible en
- Sea un elemento primo de Probar que su conjugado también es primo.
- Sea probar que no está en Sea
Probar que es un dominio de integridad, que cada elemento de puede escribirse de una única manera como
Hallar una descripción el cuerpo de fracciones de
- Sea un monoide cancelativo, es decir que Imitar la construcción del cuerpo de fracciones, para construir un grupo que contiene una copia de y donde cada elemento de es invertible. (Por ejemplo, si el monomio es el grupo será )
- es decir que es la sucesión que tiene todos sus términos nulos, con la excepción del --ésimo que es igual a 1.
- para todo en
- Por inducción sobre implica que También, Supongamos que para se cumple que Entonces,
El único sumando con es aquel donde y, por lo tanto, el correspondiente es igual a Lo que implica que Por inducción, se tiene el resultado.
- Ejercicio.
- Probaremos primeramente que
Suponer el resultado para todo Es decir que para todo en se cumple que Entonces,
El resultado sigue por inducción.
- Cada uno de los 's se llama un coeficiente del polinomio
- Cualquiera de los coeficientes puede ser nulo. Cuando todos los coeficientes sean nulos, diremos que se trata del polinomio nulo o cero.
- Cada uno de los sumandos que aparecen en la definición de se llama un término del polinomio. Cada término es de la forma donde es un elemento del anillo y es un número entero tal que llamados, respectivamente, el coeficiente del término y el grado del término. Dicho termino es el s--ésimo término. Cuando el coeficiente de un término es cero, se puede eliminar de la presentación del polinomio. Por ejemplo, podemos escribir como
- El primer sumando, es el término constante. Como cuando dicho término tiene grado 0. Los términos constantes se identifican con los elementos de
- Supongamos que no es el polinomio nulo. Entonces, al menos uno de los coeficientes de no es nulo. Sea el mayor de los enteros tales que Decimos que el término es el término líder del polinomio y que es el coeficiente líder del polinomio. En tal caso, llamamos grado del polinomio al numero Por lo tanto, el grado de un polinomio no nulo es siempre un número entero positivo o cero, al que denotaremos por Por definición de grado, para todo se tiene que si entonces
- Cuando el coeficiente líder sea igual a 1, diremos que se trata de un polinomio mónico.
- El polinomio nulo no tiene coeficiente líder, por lo que según la definición dada arriba no tiene grado. Resultará conveniente adoptar el siguiente convenio para el grado del polinomio cero
Notemos que esa definición garantiza que el polinomio nulo tiene un grado menor que cualquier polinomio no nulo.
- Cuando dos polinomios y son escritos como sumatoria de términos, los polinomios son iguales, ssi, ambos son nulos o, tienen igual grado y los coeficientes correspondientes iguales.
- Sea el anillo Sean Hallar usando directamente las definiciones de operaciones con sucesiones.
- Sean y polinomios en Hallar
- Efectuar las operaciones indicadas en simplificar las expresiones resultantes y ordenarlas por orden creciente de los exponentes de los monomios.
- Efectuar las operaciones indicadas en simplificar las expresiones resultantes y ordenarlas por orden decreciente de los exponentes de los monomios.
- Usar el método de coeficientes separados para realizar las operaciones indicadas en
- ;
- ;
- y
- Completar las demostraciones de las proposiciones, cuando lo requieran.
- Probar que cuando es un anillo conmutativo, también lo es.
- Hallar dos polinomios y en tales que el grado de la suma de con sea inferior a los grados de cada uno de los sumandos, pero que
- Hallar polinomios en tales que el grado del producto sea inferior a la suma de los grados de los factores.
- ¿Cuántos polinomios distintos de segundo grado, de tercer grado, ... , de enésimo grado podemos formar sobre el cuerpo ?
- Sean y elementos de Hallar
- Sean y dos series en Hallar el producto de con
- Hallar tales que:
- Hallar un polinomio tal que
- Hallar las relaciones entre y para que el polinomio
sea un cuadrado perfecto.
- Cuando es un dominio de integridad, los únicos polinomios invertibles en son aquellos de grado cero y cuyo coeficiente líder es una unidad de
- Sea Obtener el polinomio en la indeterminada que se obtiene de al sustituir por
- Sea un polinomio de segundo grado sobre un cuerpo Probar que hay una sustitución del tipo que convierte a en un polinomio cuyo coeficiente del término lineal es nulo.
- Sea un polinomio de tercer grado sobre un cuerpo Probar que hay una sustitución del tipo que convierte a en un polinomio cuyo coeficiente del término cuadrático es nulo.
- Sean , \ldots elementos de un anillo conmutativo Expandir cada uno de los polinomios siguientes sobre y representar la expresión resultante como un nuevo polinomio. Generalizar los resultados.
- Sean indeterminadas sobre un anillo conmutativo con identidad Entonces:
Donde,
- Sean elementos de un anillo conmutativo. Hallar una fórmula para
- Sea Sean en tales que y para todo número Hallar
- Sean en tales que Escribir de forma explícita como sucesiones a y Hallar
- Simplificar en ---el cuerpo de las fracciones racionales sobre ---las siguientes fracciones.
- Cuando es un dominio de integridad, el anillo de series formales con coeficientes en también lo es. El cuerpo de fracciones de se denota por
Como polinomios son series de potencias, se tiene que los polinomios no nulos son invertibles en
Probar que en se cumple que:
- Sea Entonces,
- Sea Entonces
- Evaluar cada uno de los siguientes polinomios de en los números indicados a continuación.
- Para cada uno de los números siguientes verificar que se trata de un número algebraico, hallando de manera explícita un polinomio anulado por ese número. En cada caso indicar si el número es, o no, un entero algebraico.
- Sean y anillos con identidad y sea un homomorfismo de anillos y sea un elemento de que permuta con los elementos de la imagen de Probar que hay un único homomorfismo de anillos tal que
- Sea en y sea una matriz Probar que es un cero de o sea que es la matriz nula.
- Sea en y sea una matriz Probar que es un cero de
- Sea un anillo conmutativo con identidad. Sea tal que
es un homomorfismo de anillos con identidad.
- Sea Sea el conjunto de todas las sucesiones Con operaciones punto a punto, o sea que
Verificar que es un anillo conmutativo con identidad. Probar que el polinomio de tiene infinitos ceros.
- Dividir por para obtener cociente y residuo Si tenemos que es el MCD buscado, y se concluye la búsqueda. En caso contrario, ir al siguiente paso.
- Continuar dividiendo divisor y residuo obtenidos en el paso anterior, repitiendo el proceso cuantas veces sea necesario hasta obtener un residuo nulo. El último divisor no nulo es el mcd buscado
- Un polinomio de es irreducible (en ), ssi, no es nulo ni una unidad y implica que o es una unidad.
- Un polinomio de es primo (en ), ssi, no es nulo ni es una unidad y cuando entonces o
- Hallar el cociente y el residuo de la división del primer polinomio por el segundo en
- 2.
- Hallar y de modo que sea divisible por
- Efectuar la división de por y determinar condiciones para que el residuo sea nulo.
- Para cada uno de los siguientes pares de polinomios, indicar si el primer polinomio tiene como factor al segundo. En caso contrario, hallar un mcd de ambos polinomios.
- Hallar el MCD y MCM de los conjuntos siguientes de
polinomios en
- Hallar números complejos de manera que sea divisible por
- Hallar el residuo de la división del polinomio por por y por
- Los residuos de la división de un polinomio por y son respectivamente 3, 7 y 13, Hallar el residuo de la división de por
- Sea un entero positivo,
- Probar que cada polinomio puede expresarse de manera única como
- Probar que el residuo de la división de cualquier polinomio por es igual a:
- Probar que cada polinomio puede expresarse de manera única como
- Probar la validez del algoritmo de Euclides (por divisiones sucesivas) para computar un mcd de dos polinomios.
Para hallar el MCD de y (suponiendo grado de mayor o igual que el grado de ), Se procede de la siguiente manera:
Coloquemos y
- [(i)]
- Se divide por y se halla el cociente y el residuo
- Si el residuo es 0, es el máximo común divisor. En caso contrario, se repite el procedimiento con y
Cuando se computa a mano, puede resultar conveniente reemplazar en algunos de los pasos, un polinomio por un asociado.
- Hallar el máximo común divisor de los siguientes conjuntos de polinomios de
- y
- y (Para evitar fracciones en la primera división, multiplicar el primer polinomio por 2, obteniendo un asociado conveniente.)
- y
- y
- y
- y
- y
- y
- Mostrar que cuando el polinomio es primo con los polinomios y (un máximo común divisor es 1), también lo será con
- Mostrar que si los polinomios y son primos entre sí, también lo serán y
- Sobre el cuerpo hallar un polinomio de grado 2 tal que y
- Probar que los polinomios de grado 1 sobre un cuerpo son irreducibles.
- Probar que en dos polinomios son asociados, ssi, son iguales.
- .
- .
- &
- De acuerdo con la definición,
- Ejercicio.
- Ejercicio.
- Sean y Entonces,
Luego,
- Si tiene un factor múltiple entonces y no son relativamente primos.
- Si la característica del cuerpo es 0 y y no son relativamente primos, entonces tiene un factor múltiple.
- Supongamos que en con y Entonces, por la regla del producto, se tiene que
(*)
Lo que prueba que es un divisor común de y - Sea tal que y sea un factor irreducible de Entonces, para algún polinomio Luego, Como sigue de la relación anterior de que Luego, como es irreducible (y, por lo tanto, primo) o Supongamos que entonces y tenemos que es un factor múltiple de Si la característica del cuerpo es 0, entonces implica que
- Hallar el residuo en cuando
- se divide por
- se divide por
- se divide por
- se divide por
- Sea un cuerpo y en Probar que
- Si entonces es irreducible.
- Si o es irreducible, ssi, no tiene ceros en
- Dar ejemplo de un polinomio que es reducible sobre pero que no tiene ceros racionales.
- El residuo de un polinomio de cuando se divide por es ¿Cuál es el residuo de cuando se divide por ?
- Sea en un polinomio tal que su residuo al dividir por es y cuando se divide por su residuo es Hallar el residuo de la división de por
- Hallar todos los ceros de en cuando
a) y b) - (Requiere Cálculo Infinitesimal.) Todos los polinomios con coeficientes reales. Como la característica es cero, cada polinomio define de manera única una función polinomial. Probar las siguientes afirmaciones.
- Cada polinomio de grado impar mayor que 1 no es irreducible.
- Suponer que en es un cero de es un cero múltiple, ssi, la tangente a la gráfica de en es el eje
- Si no tiene ceros múltiples y tiene grado impar, la cantidad de ceros reales es impar.
- Probar que el producto de dos polinomios mónicos es mónico.
- Probar que en primo se cumple que
(Sugerencia: mirar el teorema de Fermat.)
- Hallar una función de en que no es una función polinomial.
- Probar que todas las funciones de en son polinomiales.
- Probar que en el ideal es primo pero no es maximal.
- Sea un cuerpo finito que tiene elementos. Sea un polinomio irreducible de de grado ¿Cuántos elementos tiene el cuerpo ?
- Sea un anillo conmutativo con identidad y sea el conjunto formado por todas las funciones de en Para y en definir suma y producto tales que
¿Es un anillo?
- (Sustituciones) Sea un anillo conmutativo con identidad. Probar que la función tal que en es un automorfismo de anillos. Hallar condiciones suficientes sobre para que la función sea un automorfismo de anillos.
- Sea un cuerpo cualquiera. Probar que en cuando dos polinomios son mónicos, de igual grado y uno de ellos divide al otro, los polinomios son iguales.
- En hallar para cada uno de los pares de polinomios indicados un mcd. de ellos y expresar ese mcd como una combinación lineal de los polinomios dados (Teorema de Bezout)
- y
- y
- y
- Sean y polinomios en un cuerpo cualquiera. con Sean y el cociente y el residuo de la división de por Probar que
- Sean y polinomios no ambos nulos de y sea Probar que hay polinomios y en tales que pero con y
- Hallar las expansiones --arias de cada uno de los siguientes polinomios en cuando
- (Fracciones Parciales) Sean y polinomios con coeficientes en un cuerpo que son primos entre sí. Probar que siempre podemos hallar polinomios y tales que:
Mostrar, además, que podemos seleccionar y de modo que y
- (Fracciones parciales) Sea un irreducible de cuerpo. Probar que para todo polinomio tal que es posible hallar elementos en tales que
- (Fracciones parciales) Sea un polinomio mónico con coeficientes en un cuerpo Suponer que la factorización de en irreducibles está dada por donde cada es irreducible y
Sea un polinomio cualquiera tal que el grado de es inferior al grado de
Probar que hay polinomios tales que y que cumplen con
- Hallar la expansión en fracciones parciales de las fracciones siguientes.
- Los Racionales son el cuerpo de fracciones del dominio , y
- Cada número entero no nulo puede expresarse como una unidad por un producto único de potencias de primos.
- El polinomio es irreducible en ya que satisface el criterio de Eisenstein con .
- Sea un entero primo. Sea
Nos interesa probar que es irreducible en . (Por lo que todos sus ceros serán irracionales.) Claramente, el criterio de Eisenstein no es aplicable, al menos directamente. Pero el siguiente truco lo hace. Sea
Por el criterio, es irreducible. Esto implica que es también irreducible. Ya que si se tendría .
- Hallar un polinomio primitivo que sea un asociado de
- .
- .
- Hallar todos los ceros racionales de
- .
- .
- Probar que un polinomio mónico de es primitivo.
- Probar que es irreducible en , probando que es irreducible sobre . (Sugerencia: probar que no tiene factores lineales ni cuadráticos. Para lo último usar que el único polinomio cuadrático de es .)
- Probar que si es un DFU, entonces es un DFU, donde son indeterminadas sobre .
- Probar que es irreducible en . (Sugerencia. y es primo (irreducible) en .)
- Sea donde es una indeterminada sobre . Probar que es irreducible en .
- Factorizar los siguientes polinomios sobre
- .
- .
- .
- ¿Cuáles de los siguientes polinomios son irreducibles sobre ?
- .
- .
- .
- .
- .
- .
- Probar que si y son números enteros tales que y no es un cuadrado en , entonces es irreducible en .
- Si entonces donde es el módulo o largo de que es igual . El ángulo es el argumento de y está definido por .
- El módulo de es 1.
- .
- .
- .
- Para todo , tiene coeficientes enteros, es decir que
- Los ceros del polinomio de la derecha en a) son las raíces primitivas --ésimas para , que también son ceros del polinomio de la derecha. Supongamos que , fuera un cero del polinomio de la izquierda, entonces es también una raíz primitiva --ésima para algún , por lo que es un cero del polinomio de la derecha. Luego, ambos polinomio son mónicos y tienen los mismos ceros, ninguno de ellos múltiple, deben ser el mismo polinomio.
- (Por inducción sobre ) Claramente, es un polinomio en . Usando la identidad probada en a), tenemos que
Por inducción, . Dividiendo por en , obtenemos y únicos en tales que con y y en . Aplicando la unicidad para polinomios en obtenemos que y , lo que prueba la afirmación. \qedhere
- Hallar , para .
- Hallar , para primo.
- Sea donde y primos diferentes. Probar que
- Verificar que los polinomios , para son irreducibles sobre los enteros. ¿Cuáles de esos polinomios son irreducibles sobre y ?
- Un elemento de se dice que es una raíz primitiva módulo , ssi, el grupo multiplicativo es cíclico y generado por . Es decir que el orden (multiplicativo) de es , donde es la función de Euler. Hallar raíces primitivas, si existen, en:
- , , .
- , , .
- (Existencia de raíz primitiva en cuerpos finitos.) Sea un cuerpo finito con elementos. Entonces, poniendo tenemos que es un grupo con orden . Sea el mínimo común múltiplo de los ordenes de los elementos de . Probar las siguientes afirmaciones.
- Cada elemento de es un cero de , luego .
- Por el teorema de Lagrange, para cada en , , luego .
- , por lo que hay un elemento de orden en .
- Probar las siguientes relaciones sobre los polinomios ciclotómicos en .
- cuando es impar.
- .
- Si entonces en .
- Cada polinomio con coeficientes reales o complejos siempre tiene un cero complejo. (Albert Girad, 1629)
- No hay polinomios irreducibles en de grado mayor que 2.
- Sea un número complejo que no es real. Sean y números reales tales que . Probar que . (Tomar conjugados en la relación ).
- Sea un polinomio en , donde es un cuerpo cualquiera. Probar que si es un cuadrado prefecto en , digamos que , entonces los ceros de en están dados por la "fórmula cuadrática",
- Probar que , donde tiene dos soluciones complejas y (Use la relación de Moivre)
- Sea un número real positivo. Probar que los ceros de son de la forma , , donde es una raíz enésima primitiva de la unidad.
- El número real es algebraico sobre ya que es un cero de .
- Cada número racional es algebraico sobre ya que es un cero del polinomio de .
- El número complejo es algebraico sobre , ya que es un cero de .
- Sea y . Como () es un elemento de , se tiene que la adjunción de a produce un cuerpo . Probar que . Es decir que cualquier fracción de expresiones polinómicas en se puede expresar de la forma con y reales.
- Probar que no puede haber un cuerpo tal que .
- Sea una extensión de un cuerpo . Si es una extensión de , es también una extensión de .
- Sea un dominio de integridad contenido en un cuerpo . Probar que el cuerpo de fracciones de está contenido en .
- Sea una familia de cuerpos que contienen a un conjunto . Sea la intersección de todos esos conjuntos. Probar que es un cuerpo que contiene a .
- Escribir una demostración para la proposición 1.
- Sea algebraico sobre un cuerpo . Probar que el conjunto de polinomios en que tiene a como uno de sus ceros es un ideal de .
- Sea algebraico sobre . Sea un polinomio irreducible sobre tal que . Probar que , , es igual a un polinomio de grado a lo más en . (Esta es una generalización de un ejemplo del texto)
- ;
- es un múltiplo de ;
- , donde es un múltiplo de .
- Sea , donde no es un cuadrado perfecto en . Claramente, el polinomio minimal de es . Entonces, .
- ¿Cuál es el polinomio minimal de sobre ?
Sea el polinomio minimal pedido. Como no es racional, el grado de será mayor que 1. El siguiente cálculo nos proveerá con un polinomio anulado por .
Se verifica que es irreducible, por lo que se trata del polinomio minimal deseado.
- ¿Cuál es el polinomio minimal de sobre ?
Sea el polinomio minimal pedido. Repitamos el cálculo anterior, pero considerando que elementos de son ahora
admisibles como coeficientes.
Es fácil ver, entonces, que , es el polinomio minimal deseado.
- Sea .
- Probar que es irreducible en .
- Hallar polinomios del menor grado posible congruentes módulo a cada uno de los siguientes polinomios:
- , , .
- .
- .
- .
- Sea en . Simplificar .
- Sea . Para cada uno de los siguientes polinomios verificar que son irreducibles sobre y construir .
- .
- .
- .
- Sea . Probar que es irreducible sobre y construir .
- Sea . Hallar un representante de grado de
- Hallar un cuerpo con
- elementos;
- elementos; y
- elementos.
- Sea y sea en .
- Probar que la factorización de en irreducibles de es .
- Probar que y que . Por lo que no es un dominio de integridad.
- Hallar el grupo de unidades de y probar que es cíclico de orden 3.
- Sea un elemento algebraico sobre un cuerpo . Entonces, es algebraico sobre cualquier extensión de que contenga a .
- Hallar cuerpos y elemento de tal que es algebraico sobre , pero no lo es sobre .
- Sea un número entero positivo que no es un cuadrado perfecto. Sea . Probar las afirmaciones siguientes:
- Las potencias naturales de son o un entero o un entero multiplicado por .
- Sea un entero positivo. Entonces, es un racional o un racional multiplicado por .
- Probar que . Si ponemos , y . ¿Qué relación hay entre , , y ?
- Hallar el polinomio minimal sobre de cada uno de los siguientes números complejos.
- Hallar los polinomios minimales sobre de cada uno de los siguientes números complejos: , , , , , . Probar que si es cualquiera de esos números, entonces .
- Sean y dos números algebraicos y que hay polinomios y en tales que y que . Probar que .
- Sea el conjunto de polinomios en que se anulan en un elemento de una extensión de que es algebraico sobre . Probar, usando directamente la definición de ideal, que es un ideal de .
- Probar que el polinomio minimal de un elemento algebraico sobre un cierto cuerpo es irreducible sobre .
- Sea un cero de un polinomio irreducible de grado mayor que 1. Probar que si es un polinomio que tiene a como uno de sus ceros, entonces cada cero de es también un cero de .
- Sea . Sea uno de los ceros del polinomio .
- Verificar que es irreducible.
- De acuerdo a la teoría, podemos escribir cada elemento de de la forma , con racionales. Escribir de esa forma, cada uno de los siguientes elementos de . , , , , .
- (*) Probar que el conjunto de números algebraicos es cerrado respecto a la suma y a la multiplicación.
- Cada cuerpo intermedio tiene asociado un subgrupo de formado por todos los elementos de que fijan (los elementos de) .
- Cada subgrupo de tiene asociado un subcuerpo de formado por los elementos de que quedan fijo para todos los automorfismos en .
- Probar el Teorema de Galois (Proposición 10).
- (Usando la notación de la proposición "Teorema de Galois".) Sea una extensión de un cuerpo y sea .
- Sea un subgrupo de , ¿qué relación hay entre y el subgrupo de de los elementos que fijan el cuerpo intermedio de los elementos fijos por , ?
- Sea un cuerpo intermedio entre y . ¿qué relación hay entre y el subcuerpo fijo por ?
- Sea un polinomio irreducible, mónico y de grado en que tiene ceros simples , , en el cuerpo de descomposición de . Sea .
- Probar que cada de permuta los ceros de . (Ver que al aplicar a , no cambia.
- Concluir que .
- Sea el cuerpo de descomposición de de . Hallar el grupo de automorfismos de .
- y
- si además, , entonces es un grupo cíclico que es igual a e isomorfo al producto de grupos . Se cumple que .
- Si está en la intersección de con , su orden, que es mayor que 1, es un divisor de y , contradiciendo la hipótesis de relativamente primos de esos números.
- Los elementos de son todos los productos de la forma con , los 's en y los en . La hipótesis de conmutatividad dice que cada una de esas expresiones es, entonces, igual a una expresión con , y , . Esto dice que . Como la otra inclusión, siempre es válida, se tiene la igualdad anunciada. Notemos, además, que resulta entonces que el grupo es abeliano. Probaremos, a continuación, que la representación como producto de un elemento de por un elemento de es única. Sean en , en . Entonces,
En la última igualdad, el elemento de la izquierda es un elemento de , mientras que el elemento de la derecha es un elemento de . Luego, ambos elementos deben ser igual al neutro del grupo. Lo que prueba que y . Por lo tanto, la función tal que -- en , en --es biyectiva. Además,
Lo que prueba que es un isomorfismo de grupos. Si se tiene que , de donde y . Luego, por ser y relativamente primos, . Esto implica que el orden de en es divisible por . Pero como, , concluimos que el orden de es , lo que implica que y su isomorfo son cíclicos.
- , por el lema. Por lo que la suma de dos ceros de es otro cero de .
- ; por lo que, el opuesto aditivo de un cero es otro cero. Notemos que la relación anterior es válida aún cuando , ya que en ese caso siempre se tiene que .
- ; o sea que, el producto de dos ceros de es nuevamente un cero de .
- , ya que todos los polinomios de grado 1, son de la forma con en .
- Sea un primo. Como los divisores de son 1 y se tiene, por la relación (*), que . Despejando, se tiene que
Ejemplo. . Por inspección, dichos polinomios son y .
- Sean primos diferentes. Aplicando (*) con se tiene que
Por lo que
Ejemplo. .
- Sea un primo. Entonces .
Aplicando la fórmula (*), se tiene que
Aplicando la fórmula (*) a la sumatoria, se tiene que , de donde se obtiene el resultado.
- Sea cualquier cuerpo finito. Probar que no hay elementos en que sean transcendentes sobre el cuerpo primo de .
- Usar el resultado de la proposición 11.2 para probar que un subgrupo finito del grupo multiplicativo de un cuerpo es cíclico. Aplicar lo anterior para otra prueba de la proposición 11. (Sugerencia: probar que , por el teorema de Lagrange, y que considerando los ceros de . )
- (Automorfismos de ) Sea tal que . Probar las afirmaciones siguientes.
- es un automorfismo de que deja fijo a los elementos de (o sea que, en implica que ).
- Sea un entero tal que . Entonces, (la composición de consigo misma veces) es un automorfismo de tal que .
- Probar que si para todo en se cumple que , entonces . .
- (Automorfismos de (continuación).) Sea un automorfismo cualquiera de que fija los elementos de . Sea un generador del grupo cíclico . Sea en el polinomio minimal de sobre . tiene grado .
- Aplicar el automorfismo a la relación , para concluir que también es un cero de .
- Si se conoce se conoce el valor de en cualquier elemento de .
- Todas las opciones para son los ceros de . Por lo que hay, posibles automorfismos de .
- Todos los automorfismos de son aquellos del ejercicio anterior.
- En la demostración de la existencia de un cuerpo con elementos se uso que cuando un polinomio y su derivada no tienen factores comunes, los ceros del polinomio son simples. Esto solamente había sido probado para característica cero. Suponiendo que la derivada no es el polinomio nulo, probar lo anterior en característica .
- Sea .
- Probar que los únicos polinomios mónicos cuadráticos irreducibles en son: , y .
- Probar que es irreducible en .
- Sea . Hallar el cardinal del cuerpo . Sea . Hallar tal que .
- Listar todos los polinomios mónicos irreducibles de grado 3 de .
- Listar todos los polinomios mónicos irreducibles de grado 4 de .
- Sea .
- Probar que es un cuerpo con 27 elementos.
- Hallar todos los subcuerpos de .
- Hallar .
- En , hallar los recíprocos de (i) , \quad (ii) .
- cada elemento de que no es ni nulo ni unidad, es un producto de elementos irreducibles, y
- si donde los 's y los 's son irreducibles, se cumple que y que, eventualmente después de una reenumeración de los 's, se cumplirá que
- El anillo es un DFU. Sigue, de la definición general de irreducible, que si es irreducible también lo es y no hay otro asociado con él. Podemos seleccionar como representante de la clase al número positivo de la clase.
- El anillo de los polinomios con coeficientes en un cuerpo es un DFU (ver el Teorema A del capítulo La Factorización de Polinomios). En cada clase de equivalencia, siempre hay un polinomio mónico, al que podemos usar como representante predilecto de la clase.
- cada irreducible es primo y
- se cumple la condición de cadenas finitas de divisores propios.
- (i). cada par de elementos tiene MCD y
- (ii) se cumple la condición de cadenas finitas de divisores propios.
- Probar que la relación "ser asociado con" es una relación de equivalencia.
- Sea un DFU. Probar que si entonces donde es el elemento tal que cuando
- Sea un DFU. Sean elementos de Probar que si y que entonces
- Escribir la prueba de que cuando es un DFU, entonces también lo es el anillo de polinomios sobre en indeterminadas,
- es primo;
- es irreducible;
- El ideal es maximal, por lo que es un cuerpo.
- Sean y elementos de un DIP. Probar que el generador del ideal es un mcm de y
- Sea un entero primo. Sea Probar que es un DIP.
- Sea Sea Describir la estructura de (Escribir su tabla de multiplicación). Hallar un ideal maximal de
- Sea Probar que cada ideal de es principal. Hallar los ideales primos y maximales y verificar que no todos los ideales primos son maximales.
- Sea un DIP. Probar que un ideal primo es o o o un ideal maximal.
- Si entonces y
- Para todo a,b en hay elementos y tales que
con tal que o
- Sea una estructura euclídea en un dominio Definamos por donde es un entero fijo. Probar que también es una estructura euclídea en Es decir que, sin perdida de generalidad, siempre se puede suponer que la estructura es tal que para todo elemento no nulo
- Sean y elementos de Hallar un máximo común divisor de y junto con enteros gaussianos tales que
- (Primos en ) Sea un elemento primo de tal que Probar que o es un entero primo de la forma En caso contrario, probar que donde es un entero primo de la forma ¿Cuáles enteros primos son primos Gaussianos?
- Sea un raíz cúbica de la unidad. es un dominio de integridad. Sea
- Sea Probar que y que
- Probar que en es una unidad, ssi,
- Probar que si es un entero primo, entonces es irreducible en
- Probar que es irreducible.
- Probar que es un dominio euclídeo.
- Sea un dominio euclídeo. Probar que podemos computar el mcd de dos elementos usando un algoritmo análogo al existente por los enteros.
- tiene un único elemento de orden 2.
- Si entonces no contiene elemento de orden 4
- Si entonces tiene dos elementos de orden 4, que son soluciones de la congruencia
- Como hay un único subgrupo de orden 2, que será Es decir que es el elemento buscado.
- Como no puede haber elemento de orden 4.
- Como hay un subgrupo de orden 4, que tiene dos generadores, que son elementos de orden 4..
- Los primos enteros de la forma y sus asociados en
- Enteros gaussianos cuya norma es un primo entero, ya sea 2 o de la forma
- Probar que en
- Hallar todos los primos gaussianos cuya norma es igual a 2.
- Probar que en implica que Dar un ejemplo de que el converso no es válido.
- Probar usando solamente análisis de normas que no es un primo gaussiano.
- Si es un primo entero que no es un primo gaussiano, entonces para algún en
- Si es un entero primo tal que entonces no es un primo gaussiano.
- Sea un primo entero, probar que si entonces es de la forma
- Probar que le grupo de las unidades de es isomorfo a
- Hallar un mcd de y
- Probar que para todo se cumple que el polinomio es irreducible sobre
- (Prueba Alternativa del lema H), Sea un entero primo impar.
- (Existencia de elemento de orden 2) Verificar que para concluir que tiene orden 2 en Considerar cualquier con orden 2, y verificar que por lo que o Usar lo anterior para concluir que
- (Ausencia de elementos de orden 4, si ) Usar teorema de Lagrange.
- (Existencia de elementos de orden 4, cuando ). Sea cuyo orden en Por teorema de Cauchy. hay un elemento de orden 2 en Luego, por lo que tiene orden 4 en
- Si cualesquiera de esos números fuera 1, tendríamos que o serían unidades.
- Si fuera un unidad, entonces una contradicción.
- Si fuera una unidad, entonces debe ser que es lo que queríamos probar.
- Las alternativas 3 o 7 son imposibles porque no hay elementos con ese tamaño en
- Finalmente, si uno de ellos fuera 21, el otro sería 1, y estaríamos al comienzo de nuestro análisis.
- Sean elementos de un dominio. Probar que ssi, y son asociados.
- Probar que la relación de "ser asociado con" es una relación de equivalencia.
- Sea Definir (conjugado como complejo)
- Verificar que y que
- Probar que es un dominio.
- Probar que
- Probar que
- Probar que es una unidad, ssi, Hallar las unidades de
- Probar que para todo número complejo hay un elemento de tal que
- Probar que es un dominio euclídeo.
- Probar que es primo en
- Sea
- Probar que es un dominio contenido en .
- Probar que es una unidad.
- Probar que hay infinitas unidades en
- Una función de en se simboliza por . Llamamos dominio o conjunto de partida de la función al conjunto , mientras que el conjunto es el codominio o conjunto de llegada de . La flecha representa la regla de la función, o sea lo que asigna a cada elemento de un elemento de .
- Supongamos que es una función del conjunto en el conjunto . Sea un elemento del conjunto y sea el elemento de asignado por a . Nos referimos a esa situación por cualesquiera de las expresiones siguientes.
- El valor de en es .
- envía en .
- La imagen por de es .
- asigna a , el elemento .
- .
- Supongamos que es una función de en . Podemos simbolizar la regla de asignación por . Cuando queramos mencionar el nombre de la función, lo hacemos de una de las dos maneras siguientes:
La expresión se lee como "la función del conjunto en el conjunto tal que asigna a cada de el elemento de ". Ejemplo: .
- Llamamos la imagen de al subconjunto de denotado por y definido como el conjunto formado por todos elementos de que son imagen de algún elemento de
.
- Simbolizamos por al conjunto formado por todas las funciones de en . En algunos textos, se escribe , para denotar a .
- (Igualdad de Funciones.) Decimos que dos funciones, y , en , son iguales, y escribimos , ssi, y asigna el mismo elemento de a cada uno de los elementos de . Simbólicamente, .
- (La función identidad) En cada conjunto hay al menos una función del conjunto en si mismo, la función identidad que asigna a cada elemento de el mismo elemento, a la que simbolizaremos por o o simplemente (cuando el conjunto es claro del contexto). Es decir tal que
- Sea un subconjunto de . La relación de inclusión define una función tal que . Simbolizamos a esa función por
- Decimos que es suprayectiva o que es una suprayección, si, para todo en , la ecuación tiene al menos una solución.
Algunos textos, llaman epiyectivas a estas funciones.
- Decimos que es inyectiva o que es una inyección, ssi, para todo en , la ecuación tiene a lo más una solución, o sea que si tiene solución, dicha solución es única. Por lo que cuando dos elementos de tengan la misma imagen por , serán iguales.
- Decimos que es biyectiva o que es una biyección, si, para todo en , la ecuación tiene exactamente una solución. Claramente esto pasa cuando la función es inyectiva y suprayectiva a la vez.
- La identidad es una biyección en cualquier conjunto.
- La función definida por la inclusión de un subconjunto es inyectiva, por lo que decimos que se trata de la inyección canónica. Tal función no es suprayectiva, a menos que el subconjunto coincida con el conjunto.
- La función de en que asigna a cada número real el cuadrado de dicho número no es ni inyectiva ni suprayectiva, ya que la ecuación tiene dos soluciones y la ecuación no tiene solución.
- La función de en (reales positivos junto con el cero) en si mismo que asigna a cada número real su cuadrado es suprayectiva, pero no inyectiva. Ya que, tiene como soluciones a .
- Sea un conjunto y una relación de equivalencia en . Simbolizaremos por al conjunto cociente de respecto a esa relación. La correspondencia que asigna a cada en su clase de equivalencia en es una suprayección.
- Sean y dos conjuntos cualesquiera. La función de en (resp. en ) que asigna a cada par su primera (resp. su segunda) coordenada es una función suprayectiva, llamada la primera (resp. la segunda) proyección.
- .
- .
- Las funciones inyectivas son cancelables por la izquierda.
Es decir, cuando es inyectiva se cumple que:
- Las funciones suprayectivas son cancelables por la izquierda. Es decir, cuando es suprayectiva se cumple que:
- Las funciones biyectivas son cancelables por derecha e izquierda y coinciden con las funciones invertibles.
- Llamamos imagen directa de a la función
definida para cada en por
- Llamamos imagen inversa de a la función
definida por
- , ssi, .
- .
- Si entonces .
- .
- .
- .
- .
- .
- Si entonces .
- .
- .
- , cuando .
- .
- .
- Sea . Entonces, hay un en tal que . Por lo tanto, concluimos que: (i) está en ; y (ii) que: , o sea, está en . Luego, pertenece a . Lo que prueba que, . Veamos ahora la inclusión inversa. Sea . Por lo tanto, y hay un tal que . Por definición entonces, . Lo que prueba que
- Sea , entonces, . De donde, está en la imagen inversa de .
- .
- .
- Sea . Entonces, , ssi, hay un en tal que , ssi, , ssi, .
- .
- .
- Sea . Entonces, , ssi, , ssi, , ssi, , ssi, .
- Aplicación.
- Mapeo.
- Transformación.
- Operador.
- Reflexiva, cuando para todo .
- Simétrica, cuando para todo .
- Transitiva, cuando para todo .
- Antisimétrica, cuando para todo .
- De equivalencia, cuando sea reflexiva, simétrica y transitiva a la vez.
- De orden parcial, cuando sea reflexiva, transitiva y antisimétrica a la vez.
- De orden total, cuando sea de orden y dos elementos sean siempre comparables.
- La relación de igualdad en un conjunto es una relación de equivalencia. Cuando queramos recordar a esta relación como un conjunto de pares, la simbolizaremos por o simplemente . proviene de "diagonal principal" del conjunto cartesiano .
- La relación de inclusión es una relación de orden parcial en el conjunto potencia de un conjunto.
- La relación de "menor o igual" en los números es una relación de orden total en el conjunto de los Enteros.
- Sea y una relación en . Entonces, es una relación en que llamaremos la restricción de a y que simbolizaremos por
- El conjunto de vértices del grafo es igual al conjunto .
- El conjunto de aristas del grafo está formado por todos aquellos pares tales que .
- Cada vértice se representa por un punto etiquetado con el nombre del punto.
- Cada arista se representa por un arco de curva uniendo el vértice con el vértice , con una punto de flecha del lado del vértice .
- Cada relación de equivalencia en un conjunto define una partición de , donde cada elemento de la partición coincide con las clases de equivalencia.
- Cada partición de un conjunto define una relación de equivalencia, cuyas clases de equivalencia son precisamente los elementos de la partición.
- Decimos que un elemento es un supremo o cota superior estricta o de un subconjunto , si es una cota superior tal que para cualquier otra cota superior se cumple que .
- Decimos que un elemento es un <ínfimo o cota inferior estricta de un subconjunto , si es una cota inferior tal que para cualquier otra cota inferior , se cumple que .
- La primera vía es suponer la existencia de los Reales (presentados como un cuerpo ordenado completo) y deducir la existencia y propiedades del resto de los sistemas numéricos. Esa será la vía que adoptaremos. El lector interesado puede, por ejemplo mirar a (BB) Spivak.
- La otras vía es comenzar con los axiomas de Peano para los números naturales para, posteriormente, construir los otros sistemas numéricos.
- es válida, y
- cuando un entero es válida, también lo es .
- es válida, y
- suponiendo la propiedad válida para todo , se concluye que lo es .
- Si es un número primo y entonces o .
- Si es un factor de , entonces o . Supongamos que es un factor de . Si es un factor de , no hay nada más que probar. Supongamos que no divida a . Entonces, . Luego, por Bezout, hay enteros , tales que . Multiplicando por en ambos lados de esa relación, obtenemos que . Como es un factor de , es un factor del lado izquierdo, por lo que es un factor del lado derecho, o sea de .
- Un número es compuesto, ssi, con .
- Cada número tiene un factor primo (que puede ser él mismo, cuando es primo). El resultado es válido cuando , ya que 2 es primo. Supongamos arbitrario y que el resultado es válido para números menores que . Si es primo, no hay nada más que probar. Si es compuesto, entonces , con . Por lo que tiene un factor primo, que es también un factor de .
- Se define el conjugado de como el complejo . Se verifica que la conjugación conmuta con la adición y multiplicación.
Además, es un número real que es positivo, excepto cuando .
- Se define el \textbf{módulo} del complejo como . El módulo tiene propiedades análogas al valor absoluto de los reales.
- Cada complejo puede escribirse de la forma donde , y ,
- Se verifica que .
- Definiendo se obtiene una exponencial compleja, con propiedades formales de las potencias.
- ↑ Estudiadas en cursos de Cálculo.
- ↑ (BB) Landau
- ↑ (WEB) HernandezFA.
- Una operación 1--aria es simplemente una función de en si mismo.
- Una operación binaria es una operación 2--aria.
- Una operación 0--aria se interpretará como la selección de un elemento de . Usualmente denotaremos la operación por el nombre del elemento seleccionado, a veces con un subrayado, .
- Un magma es una estructura donde es una operación binaria en . El tipo del magma es .
- Un semigrupo es una estructura donde es una operación binaria en , tal que (axioma) la operación es asociativa. El tipo de un semigrupo es .
- Un monoide es una estructura , donde es una operación binaria y es una operación 0-aria tales que se tiene los siguientes axiomas:
- [M-1] * es una operación asociativa.
- {M-2] en es un neutro para la operación .
El tipo de la estructura monoide es .
- Un grupo es una estructura , donde es una operación binaria, es una operación 0-aria y \textsf{inv} es una operación 1--aria tales que se tiene los siguientes axiomas:
- [G-1]* es una operación asociativa.
- [G-2] en es un neutro para la operación .
- [G-3] Para todo en , es un inverso de respecto a la operación .
El tipo de la estructura grupo es .
- que es una estructura subyacente de semigrupo.
- que es una estructura sin nombre especia y que especifica que >
- (la lista de operadores es vacía; solamente afirmamos que es un conjunto.
- las rotaciones, que se caracterizan por dejar exactamente un punto fijo (el centro de la rotación) y
- las reflexiones que se caracterizan por dejar todos los puntos de una línea fijos y mover los puntos fuera de la línea a una imagen especular de los mismos, usando como espejo a la línea.
- .
- .
- .
- .
- Por los trabajos de la sección anterior cuando sea cualquier múltiplo escalar no nulo de , tendremos que . Por razonamientos anteriores, vemos que cualquier vector no nulo de sirve como vector director de la línea .
- Sean y dos puntos diferentes de la línea . Entonces, . Esto es, dos puntos diferentes de la línea determinan un vector director y, por lo tanto, a la dirección.
- Sea un punto de tal que . Entonces,
Es decir que . Es decir que la línea puede ser descrita por cualesquiera de sus puntos y la dirección de la misma.
- Sigue de lo anterior que dado dos puntos y , hay una
única línea que pasa por esos dos puntos:
- Notemos que es una línea que pasa por el origen y el punto .
- En el lenguaje de la teoría de grupos, las líneas son las clases laterales de los subgrupos de la forma .
- La composición de dos traslaciones es una traslación. En efecto, .
- La traslación por el vector nulo, es la identidad.
- Las traslaciones son invertibles, .
- (PI-1) .
- (PI-2) .
- (PI-3)Si , .
- (Determinante igual a1.)
- . .
- Etc.
Ejercicios
[editar]Ideales Principales
[editar]En el capítulo anterior vimos dos tipos especiales de ideales: primos y maximales. Recordemos que ideal es maximal, cuando no hay otro idel propio diferente de el que lo contenga. Caracterizamos a los ideales maximales I de A, como aquellos idelaes cuyo anillo cociente es un cuerpo. Un ideal J es primo cuando su anillo cociente es un dominio, o equivalentemente, cuando para todo x, y se cumple que xy en J implica que x está en J o y está en J. posteriores:ideales primos e ideales maximales.
A continuación, veremos una relación entre elementos primos e ideales principales (o sea generados por un elemento) primos.
Proposición 8. Sea un anillo conmutativo con identidad y sea un ideal principal no nulo, digamos que El ideal es un ideal primo en ssi, es un elemento primo de
-
Demostración:
() Supongamos que es un ideal primo. Si se tiene que por ser un múltiplo de es un elemento de Por ser primo el ideal, tenemos que o están en Es decir que al menos uno de ellos es un múltiplo de o sea que divide a uno de ellos. Pero eso, es precisamente la definición de elemento primo.
() Sea primo y sean en Eso implica que por lo que o Es decir que está en o está en Lo que prueba que es un ideal primo.
Ejemplo.
Los ideales de con primo, son ideales primos.
La Estructura de los Zm
[editar]Convenio. Con el fin de simplificar la notación, de ahora en adelante, usaremos los representantes canónicos para denotar los elementos del anillo . Así, en denotará la clase de () .
Los anillos proveen interesantes ejemplos de anillos. Sabemos que si es primo, es un cuerpo y que, en caso contrario, contiene divisores de 0.
Sabemos, también, que cuando con entonces
Por inducción, cuando entonces
Las Unidades de Recordemos que vimos anteriormente que un elemento es invertible, ssi, El cardinal de es donde es la función de Euler. Vimos también que, con como en la discusión anterior que
La discusión anterior reduce el problema de la estructura de a considerar el caso donde es una potencia de un primo.
Ejemplo.
Sea donde es un número primo. Consideremos el anillo cociente
Observemos que implica que Por lo que las unidades de corresponden a números que no son divisibles por Luego, un elemento de es un divisor de cero, ssi, Luego, los divisores de cero en son:
Luego, hay divisores de cero. El resto, son unidades, por lo que
Sea un ideal propio de Como no puede contener unidades, los elementos de serán múltiplos de Observemos que si se tiene que es maximal, ya que fuera de todos los elementos son unidades. Además, ese razonamiento muestra, junto con la observación anterior, que es el único ideal maximal de Sea un ideal propiamente contenido en Sea tal que es minimal respecto a que está contenido en Si o , se tiene que es una unidad, por lo que y coincidiría con Luego, Es decir que, tenemos una cadena de ideales,
Proposición 9. Sea y es un entero primo. Si es un cuerpo. Las unidades de forman un grupo de orden y los divisores de cero forman un ideal de cardinalidad que está generado por Dicho ideal es maximal y es el único ideal maximal. Todos los otros ideales son de la forma
-
Demostración: Ejercicio
Ejercicios
[editar]El Cuerpo de Fracciones de un Dominio
[editar]Recordemos que los números racionales se construyen a partir de los enteros, como un conjunto de fracciones de números enteros.
Como veremos en esta sección, hay una construcción análoga de un cuerpo a partir de cualquier dominio. Es decir que dado un dominio es posible hallar un cuerpo que estará formado por las fracciones de elementos de que se llamará, por lo tanto, el cuerpo de fracciones de Recordemos para efectos posteriores que los anillos sin divisores de cero tienen todos sus elementos cancelables. Técnicamente, el problema es cómo inventar fracciones cuando no hay división.
El problema es como inventar fracciones cuando no hay división.
Sea , el conjunto formado por todas las posibles parejas ordenadas de elementos de donde el segundo elemento no puede ser nulo. Intuitivamente, podemos imaginar a cada una de esas parejas como representando una fracción.
Introduciremos una relación en que resultará ser de equivalencia.
- Sean elementos de
Lema A.
La relación es una relación de equivalencia en
-
Demostración:
La proposición anterior implica que divide en una colección de clases disjuntas: las clases de equivalencia de
Notación. Sea el conjunto formado por todas las clases de equivalencia de
Simbolizaremos por la clase de equivalencia de o sea al conjunto formado por todos los elementos de equivalentes con Recordemos que las clases de equivalencias son disjuntas entre sí y que su reunión es todo el conjunto
Los resultados del siguiente lema se usarán sistemáticamente más adelante, en especial la parte a.
Lema B. Sean elementos de tales que Entonces,
-
Demostración:
Introduciremos operaciones en mediante las siguientes definiciones.
Lema C.
Las operaciones anteriores están bien definidas, o sea, no dependen de los representantes escogidos.
-
Demostración: Supongamos que y que
Debemos verificar que y que
Es decir que, para la adición, se cumple que Como
Análogamente, para la multiplicación, deberemos probar que Como se tiene el resultado.
Proposición 10. (Estructura de Cuerpo de )
tiene una estructura de cuerpo.
-
Demostración: ( es un grupo abeliano.)
Sigue inmediato de la definición que la adición es conmutativa en
Como se
concluye que es un neutro respecto a la adición.
Como
concluimos que cada elemento tiene opuesto aditivo.
Finalmente probaremos que la operación es asociativa. Sean
y elementos de Entonces,
Veremos, ahora, que hay un subanillo de que es isomorfo a Identificando con ese subanillo de consideraremos a un subconjunto de
Sea tal que envía cada elemento de en el elemento de Tenemos, en primer lugar que, cuando se cumple que o sea que Es decir que se trata de una función inyectiva.
Además, tenemos que
Lo que prueba que es un homomorfismo inyectivo de cuya imagen (que será un subanillo de es, por lo tanto, isomorfa a como anillos con identidad, ya que Identificaremos a con su imagen, es decir con las fracciones con ``denominador 1.
La identificación anterior nos permitirá escribir los elementos de de manera más simple. Como, de lo anterior, resulta que y como tenemos que
Los elementos de se identifican con las fracciones de denominador 1.
Definición. (Cuerpo de Fracciones) Llamaremos cuerpo de fracciones de un dominio al cuerpo construido arriba. El elemento se escribirá siempre como una fracción
Los elementos de son las fracciones con denominador 1, que se escriben usualmente sin usar fracciones.
El cuerpo de fracciones de un dominio tiene la siguiente propiedad universal.
Proposición 11. (Propiedad Universal del cuerpo de Fracciones) Sea un dominio de integridad y sea su cuerpo de fracciones. Sea un cuerpo cualquiera y sea un homomorfismo inyectivo de anillos con identidad. Entonces, hay un único homomorfismo de cuerpos que coincide con para los elementos de Es decir, que hace conmutativo el siguiente diagrama.
-
Demostración: Recordemos que en un cuerpo, la fracción está definida como Sean elementos de Si queremos que se cumpla la conmutatividad del diagrama debemos tener que
Usando la última relación, como definición para donde la primer fracción es en y la segunda en se ve la unicidad si esa función está bien definida y es un homomorfismo de cuerpos.
Sea entonces por lo que Por lo tanto, ; lo que implica que está bien definida, su valor no depende del representante usado de una fracción. El resto de la demostración queda de ejercicio.
Corolario 11.1. Sea un dominio y su cuerpo de fracciones. Sea un cuerpo cualquiera que contiene a entonces es isomorfo a un subcuerpo de que contiene a
-
Demostración: Aplicar la proposición a la inclusión canónica
En la situación del corolario, es usual identificar el cuerpo de fracciones con el subcuerpo isomorfo.
Cualquier cuerpo de característica cero tiene un anillo primo isomorfo a los Enteros, por lo que contienen un subcuerpo identificable con los racionales, que es obviamente el cuerpo primo del cuerpo.
Ejercicios
[editar]Ejercicios del Capítulo
[editar]Comentarios
[editar]Como hemos mencionado antes, los intentos de prueba del Último teorema de Fermat, condujeron a la creación de nuevas matemáticas. Varios matemáticos intentaron conseguir una solución en dominios de números complejos que incluían radicales. Parecía que la divisibilidad en esos dominios era semejante a aquella de los Enteros. Muchas pruebas erróneas tuvieron origen en esta creencia que siempre la semejanza era perfecta. Al descubrir situaciones donde irreducibles no eran primos llevo a profundizar el estudio de esos dominios, lo que nosotros haremos en el capítulo sobre Álgebra/Álgebra Abstracta (Primer Curso)/Contenidos/Tipos de Dominio|Tipos de dominios]].
17. Los Anillos de Polinomios
[editar]Introducción
[editar]El Álgebra se creó para la resolución de ecuaciones polinómicas. Primeramente, se estudiaron las ecuaciones lineales y cuadráticas, para extenderse posteriormente a ecuaciones polinómicas de grados superiores. En los curso básicos, los polinomios son usualmente considerados como funciones polinómicas. Examinaremos, a continuación, dicha noción y veremos que es insuficiente para nuestros propósitos. Luego de ese análisis, daremos una definición formal de polinomios con coeficientes en cualquier anillo, así como de operaciones que proveerán al conjunto de polinomios de una estructura de anillo.
Posteriormente, veremos que para polinomios con coeficientes en un cuerpo tendremos una teoría de divisibilidad análoga a aquella de los enteros..
Las Funciones Polinómicas Reales
[editar]Las funciones polinómicas reales son funciones de en tales que
donde los 's son números reales. El lector, seguramente, conoce algunas de las propiedades de esas funciones y su relación con las ecuaciones polinómicas con coeficientes reales. Claramente, podríamos generalizar tales funciones de manera que sus coeficientes pertenecieran a un cuerpo cualquiera e inclusive a un anillo cualquiera. Sin embargo, para los propósitos algebraicos necesitaremos una noción más general que llamaremos polinomio formal. Algebraicamente, los polinomios formales tendrán muchas de la propiedades de las funciones polinómicas, pero permitirán estudiar de manera más cómoda y eficiente las ecuaciones polinómicas. Los siguientes ejemplos ilustrarán la necesidad de polinomios formales.
Ejemplo.
Recordemos que un cero de una función polinómica es un número del dominio de la función tal que Consideremos la función polinómica de en tal que Observemos que un "cero" de esa función es el número irracional que no pertenece al dominio de la función.
El problema no es que la función tenga dominio los racionales y no todos los reales, ya que la función tal que tampoco tiene ceros reales, aunque sí complejos.
Es decir que un problema con las funciones y sus ceros, es que puede haber "ceros" de la función que vivan fuera del dominio de la función.
Ejemplo.
Consideremos el cuerpo y sean y funciones de en si mismo tales que y La tabla siguiente muestra los valores de las funciones.
Como para todo de se cumple que tenemos que las funciones polinómicas y son iguales, aunque sus grados son diferentes. Nosotros no queremos que polinomios de diferentes grados sean iguales, por lo que necesitaremos una noción diferente a funciones polinómicas.
Búsqueda de una definición
[editar]Queremos que nuestros polinomios formales tengan propiedades análogas a funciones polinómicas, inclusive que se escriban de manera parecida. Para buscar una definición adecuada, examinaremos las propiedades de la suma y la multiplicación de las funciones polinómicas, especialmente cuando se realizan esas operaciones por coeficientes separados---es decir, cuando solo escribimos los coeficientes.
La suma
[editar]Sean y Hallar la suma de y Las expresiones polinómicas pueden escribirse con los grados en forma ascendente, o en forma descendente. Hemos usado la forma ascendente, porque será más útil para nuestros propósitos.

A la derecha, hemos mostrado el cómputo mediante coeficientes separados, donde se ve claramente que la suma consiste en sumar los coeficientes de los términos de igual grado de los sumandos. Notemos que la notación ascendente de los polinomios, permite alinear fácilmente los términos iniciales. Si llamamos y a los coeficientes de los términos de grado de los sumandos, y si es el coeficiente del término de grado del resultado, tenemos que
| (16-1) |
Esa afirmación supone que cuando un término de un polinomio no aparece, su coeficiente es cero.
La multiplicación de polinomios
[editar]Examinaremos la multiplicación, tratando de ver el patrón de generación de los coeficientes del producto. Sean y dos funciones polinómicas. Veamos la generación de los primeros términos del producto.

Reuniendo los términos de igual grado, obtenemos que
Observemos que en cada coeficiente de un término del producto, el valor de la suma de los subíndices de cada uno de los factores de los sumandos que determinan al coeficiente, es igual al grado del término. Por lo que si llamamos al coeficiente del término de grado del producto, se cumplirá que
| (16-2) |
Observemos, nuevamente, que si no hubiésemos escrito las potencias de (método de los coeficientes separados), habríamos obtenido el resultado, efectuando los mismos cómputos. Es decir que para las operaciones lo único importante son los coeficientes y su posición dentro del polinomio, por lo que podríamos representar el polinomio
como una sucesión
Esa es precisamente la vía que adoptaremos. Nuestros polinomios formales serán sucesiones de números o, en general, de elementos de un anillo, que se operan de acuerdo a las relaciones en las ecuaciones (16-1) y (16-2), y cuyos términos son todos nulos a partir de un cierto término en adelante.
Las Definiciones Formales
[editar]Sea un anillo (conmutativo o no) con identidad. Simbolizaremos por al conjunto formado por todas las sucesiones de en es decir todas las funciones de en El valor de en se denota por y se dice que es el término --ésimo de la sucesión.
Dotaremos a de operaciones de suma y multiplicación análogas a las de la suma y multiplicación de las funciones polinómicas. Por ahora, no nos restringiremos a sucesiones que tengan solamente un número finito de términos no nulos; más tarde, consideraremos esa restricción.
La suma
[editar]Sean y dos sucesiones de La suma de esas sucesiones es la sucesión denotada por y tal que
| (16-3) |
Es decir que el término --ésimo de la suma es la suma de los términos --ésimos de los sumandos.
Notemos que la suma definida es la suma usual de sucesiones que corresponde a la suma de funciones definida punto a punto. Sabemos de trabajos anteriores que tal suma es asociativa, conmutativa, que tiene como neutro la función constante cero (para todo ), y que cada función tiene un opuesto aditivo tal que Por lo que es un grupo abeliano.
La multiplicación
[editar]Sean y dos sucesiones de Definiremos el producto de esas sucesiones por una relación idéntica a aquella en la ecuación (16-2), es decir que
| (16-4) |
Nos interesa probar que es un anillo con identidad. Para eso, nos falta por probar que la multiplicación es asociativa, distributiva y que hay una función identidad para la multiplicación.
Lema A. La multiplicación definida en (16-4) es asociativa.
-
Demostración: Sean y tres sucesiones de en Para todo se cumple que
Lo que prueba la asociatividad. (La clave de la demostración es observar que todos los sumandos son de la forma indicada en la última sumatoria.)
Lema B.
La multiplicación definida es distributiva.
-
Demostración: Sean y tres funciones de en Para todo se cumple que
Análogamente, se verifica la distributividad por la derecha.
Identificación de con un subanillo de
Con cada en asociaremos la función tal que y para todo Como sucesión, tenemos que
Sea tal que Claramente, es una función inyectiva, Probaremos que es un homomorfismo de anillos.
Cuando y son elemento de se cumple que mientras que para tenemos que Luego,
| (16-5) |
Veamos la situación con la multiplicación.
Con se tiene que
La última sumatoria es igual a cero, ya que implica que Veamos la primera sumatoria.
Como cada uno de los sumandos es nulo, se tiene que para
Luego,
| (16-6) |
Las relaciones (16-5) y (16-6) nos dicen que la función es efectivamente un homomorfismo que además es inyectivo. Por lo tanto, es isomorfo (como anillo) con su imagen. Usando ese monomorfismo, identificaremos los elementos de con sus imágenes, por lo cual consideraremos a como un subanillo de
Veamos, ahora, que sucede cuando se multiplica un elemento de por una sucesión cualquiera.
Lema C. Sean en y en Se cumple que (Es decir que cada término de la sucesión se multiplica por )
- Demostración:
Corolario C.1. Es decir que 1 es una identidad en
Todo el trabajo anterior muestra la siguiente proposición.
Proposición 1. El conjunto con las operaciones definidas arriba tiene la estructura de un anillo con identidad que contiene a como subanillo. Cuando es conmutativo, también lo es.
-
Demostración: Queda de ejercicio probar la parte de la conmutatividad de la multiplicación, cuando el anillo es conmutativo.
El Anillo de los Polinomios
[editar]Un polinomio puede considerarse, intuitivamente, como una sucesión donde todos sus términos son nulos, excepto, a lo más, una cantidad finita de ellos. Formalizaremos lo anterior, empezando con la siguiente definición.
Sea en Llamamos soporte de la sucesión al subconjunto de formado por todos los tales que
Con los preparativos anteriores, estamos listos para definir la noción formal de polinomio.
Definición. (Polinomio Formal) Sea un anillo con identidad. Un polinomio (formal) con coeficientes en es una sucesión en con soporte finito.
En términos de sucesiones, un polinomio es una sucesión con un número finito de términos no nulos. Sea
Intuitivamente, corresponde al polinomio Para obtener formalmente lo anterior, definiremos al polinomio También, deberemos probar que la suma y el producto de polinomios es un polinomio, es decir que forman un subanillo de
Previamente, introduciremos el símbolo de Kronecker que nos ayudará a expresar más concisamente nuestras definiciones y demostraciones.
Definición. (Símbolo de Kronecker) Llamamos símbolo de Kronecker a la expresión definida como:
Por ejemplo, cada elemento de define la función que es tal que
Definición. (Indeterminada) Llamamos indeterminada con respecto al anillo a la sucesión de simbolizada y tal que
Es decir que
Claramente, es un polinomio.
Proposición 2. Sea la indeterminada, entonces
-
Demostración:
Proposición 3. El conjunto de los polinomios determina un subanillo con identidad de que será denotado por y que diremos que se trata del anillo de polinomios en una indeterminada con coeficientes en el anillo ,
-
Demostración: Necesitamos tan sólo probar que la suma y el producto de sucesiones con soporte finito son sucesiones con soporte finito. Sean y dos polinomios tales que para se tiene que y para se cumple que
Entonces, si se tiene que al ser mayor que y que
Es decir que es un polinomio.
Sea ahora Entonces,
Los sumandos de la primera sumatoria tiene un factor con lo que implica que por lo que esa sumatoria es 0. Observemos que en la segunda sumatoria, se tiene que Entonces, Por lo que los 's son todos nulos, haciendo la segunda sumatoria nula. Luego, es un polinomio.
A continuación, veremos como recuperar la notación tradicional de polinomios.
Proposición 4. Sea una sucesión no nula con para o sea un polinomio. Sea Entonces,
-
Demostración: Claramente, si Sea tal que
Por lo que las dos sucesiones son iguales.
La proposición muestra como podemos expresar un polinomio como una suma finita de términos de la forma Usaremos esa notación, de ahora en adelante.
Nomenclatura
[editar]Sea un polinomio de al que expresaremos como donde (fj en la notación anterior de sucesiones).
Grados de la Suma y el Producto
[editar]Sean y dos polinomios con grados y respectivamente. Mirando a la demostración de la proposición sobre la suma y multiplicación de polinomios, vemos que tenemos cotas para los grados de la suma y el producto de dos polinomios.
En primer lugar, tenemos que el grado de la suma nunca excede el grado de los sumandos, o sea que
|
|
La desigualdad puede ser estricta, por ejemplo considerar Pero, puede haber también otras circunstancias que hagan estricta a la desigualdad anterior.
Ejemplo.
Sea (enteros modulo 6) y sean Entonces,
Con respecto a la multiplicación, tenemos que
|
|
El siguiente ejemplo muestra que la desigualdad puede ser estricta.
Ejemplo.
Sea se tiene que
El grado, en el ejemplo anterior, es menor que la suma de los grados, ya que los coeficientes lideres de los factores eran divisores de cero. Cuando uno de ellos no es un divisor de cero, tenemos la igualdad.
Proposición 5. Sean y polinomios en tales que el coeficiente líder de al menos uno de esos polinomios no es un divisor de cero. Entonces,
Además, el coeficiente líder del producto es el producto de los coeficientes lideres de los factores.
-
Demostración: Si uno de los polinomios es nulo, el resultado es trivialmente válido. Supongamos que y donde Entonces, el término --ésimo es aquel del mayor grado posible del producto. Se tiene que
Si se cumple que por lo que Igualmente, si entonces Es decir que el único posible sumando no nulo en la sumatoria anterior es Como o no son divisores de cero, se tiene que De donde el resultado.
Corolario 5.1. Cuando es un dominio de integridad, entonces también lo es.
-
Demostración: Cualquier polinomio no nulo tiene un coeficiente líder que no es un divisor de cero. Si y son polinomios no nulos, el coeficiente líder del producto es igual al producto de los coeficientes lideres de y por lo que no puede ser nulo.
Observación. Sean y anillos tales que es un subanillo de Entonces, cada polinomio en puede considerarse un polinomio en Por lo que siempre consideraremos que es un subanillo de Por ejemplo, se cumple que
Cuerpo de las Fracciones Racionales
[editar]Vimos arriba que cuando es un dominio de integridad, en particular un cuerpo, también es un dominio de integridad. Sabemos del capítulo pasado que todo dominio de integridad puede extenderse a un cuerpo de fracciones del anillo.
Definición. (Cuerpo de las Fracciones Racionales) Sea un dominio de integridad. Llamamos cuerpo de las fracciones racionales al cuerpo de fracciones del dominio de integridad Notación:
Polinomios en varias variable
[editar]Sea un anillo con identidad, entonces también es un anillo con identidad, por lo que podríamos considerar polinomios con coeficientes en Si llamamos a la indeterminada correspondiente, tendríamos el anillo con identidad que simbolizamos de forma abreviada como Usando de base ese último anillo, podemos obtener etc.
Anillo de las Series Formales de Potencias
[editar]Volvamos al anillo de las sucesiones con términos en un anillo Poniendo al igual que para los polinomios, tendremos, por la demostración de la proposición de representación como sumatoria de los polinomios, que podríamos escribir cada sucesión como un polinomio de grado infinito, o sea como una sumatoria sin fin
El lector habrá encontrado en sus cursos de Cálculo expresiones análogas llamadas series de potencias. Por tal razón, llamaremos a los elementos de series de potencias formales. Simbolizaremos a como y diremos que se trata del anillo de las series de potencias formales en una indeterminada con coeficientes en el anillo
Ejercicios
[editar]La Evaluación de un Polinomio
[editar]En esta sección, veremos como definir ceros de un polinomio. Sea un anillo conmutativo con identidad y sea el anillo de polinomios en la indeterminada con coeficientes en Supongamos que fuera un superanillo de o sea un anillo que contiene a (pero no necesariamente conmutativo), y que fuera un elemento de que conmuta con todos los elementos de (En particular, si fuera conmutativo, cualquier elemento de )
Decimos que ese elemento de es el valor de en y usaremos la notación funcional para representarlo.
Convenio Notacional.
Notemos que la notación pudiera ser ambigua, ya que si consideramos a como una sucesión o sea una función con dominio puede indicar el coeficiente --ésimo del polinomio o la evaluación de en que en general son dos cosas diferentes. Por lo que de ahora en adelante, la notación funcional se usará únicamente para la evaluación de polinomios y los polinomios siempre se presentarán como suma de términos.
Funciones polinómicas.
Cuando sea un elemento de (que es obviamente un superanillo de si mismo) entonces es un elemento de Por lo que tenemos asociada a cada polinomio de una función que diremos que es la función polinómica definida por A menos que haya un riesgo de confusión, usaremos el mismo nombre para dicha función.
Volviendo a la situación de la definición, tenemos para cada que es un elemento de una función que asigna a cada polinomio de su evaluación en Denotaremos esa función por La siguiente proposición muestra que esa función es un homomorfismo de anillos.
Proposición 6. Sean y polinomios con coeficientes en Sea un elemento de un superanillo del anillo y que permuta con los elementos de Entonces,
Luego,
-
Demostración: Ejercicio.
Sigue de la proposición que es un homomorfismo de anillos.
Proposición 7. (Extensión de Homomorfismos)
Sean y anillos conmutativos con identidad, y un homomorfismo de anillos con identidad. Entonces, hay una función
que es un homomorfismo de anillos.
Es decir que asigna a cada polinomio de el polinomio de que resulta al reemplazar los coeficientes del primer polinomio por sus imágenes por
-
Demostración: Sean y Entonces,
Nomenclatura. Decimos que es el homomorfismo inducido por
Sea el supramorfismo canónico, Entonces, diremos que el polinomio es el polinomio obtenido de por reducción módulo
Ejemplo.
La reducción de módulo 2 es igual a
Sustitución de Indeterminada
[editar]Sea un anillo conmutativo con identidad y sea es un superanillo de y cada uno de sus elementos permuta con los elementos de Por lo que podemos evaluar cada polinomio en en un elemento de o sea en otro polinomio, digamos, de El resultado se dice que es la sustitución de la indeterminada o variable por
Ejemplo.
Sea y sea
Los Ceros de un Polinomio
[editar]Definición. (Cero de un Polinomio) Sean un anillo conmutativo con identidad, un superanillo de y un polinomio con coeficientes en Decimos que un elemento de que permuta con los elementos de es un cero o raíz del polinomio ssi,
Denotaremos por (o simplemente cuando el conjunto de donde se toman los ceros sea claro del contexto) al conjunto formado por todos los ceros de en
Observación. Sea un superanillo de entonces
Ejemplo.
Sea un polinomio en Entonces, Por lo que 2 es un cero del polinomio
Se ve claramente que
Ejemplo.
Sea un polinomio en Entonces, claramente lo que prueba que es un cero del polinomio Además es el único cero en Por lo que, pero
Ejemplo.
Sea un polinomio en
Entonces, claramente lo que prueba que son ceros del polinomio Sabemos que esos números no son racionales, por lo que pero lo que indica porque no podemos omitir el anillo donde estamos considerando los ceros en la notación cuando se trabaja simultáneamente con varios anillos.
Los ejemplos anteriores muestran, además, que los ceros de un polinomio no tienen porque vivir en el anillo de los coeficientes, aunque ese anillo sea un cuerpo.
|
Dado un anillo y un polinomio en determinar todos los posibles ceros de |
Como lo muestran los ejemplos anteriores, para hallar los ceros, a lo mejor será necesario extender el anillo donde están los coeficientes del polinomio.
Números y Enteros Algebraicos
[editar]Definición. (Número Algebraico, Entero Algebraico) Un número complejo se llama número algebraico cuando es un cero de un polinomio con coeficientes en Un número algebraico es un entero algebraico cuando es un cero de un polinomio mónico con coeficientes enteros.
Ejemplo.
es un entero algebraico, ya que es un cero de
Ejemplo.
Hallar un polinomio en tal que sea un cero del polinomio.
Resolución. Pongamos Entonces,
Luego, es un polinomio con el cero indicado.
Ejercicios
[editar]18. La Divisibilidad en los Polinomios
[editar]La Divisibilidad en el Anillo de los Polinomios
[editar]El anillo de los polinomios sobre un anillo conmutativo con identidad es, a su vez, un anillo conmutativo con identidad, por lo que todas las nociones de divisibilidad sobre anillos le aplican. En particular, las nociones de unidad, elemento primo, elemento irreducible. Veremos,a continuación, que la teoría de la divisibilidad en el anillo de polinomios es semejante a la teoría de divisibilidad de los Enteros, especialmente cuando los coeficientes se toman de un cuerpo.
La Divisibilidad en el Anillo de los Polinomios
[editar]El anillo de los polinomios sobre un anillo conmutativo con identidad es, a su vez, un anillo conmutativo con identidad, por lo que todas las nociones de divisibilidad sobre anillos le aplica. En particular, las nociones de unidad, elemento primo, elemento irreducible. Veremos,a continuación, que la teoría de la divisibilidad en el anillo de polinomios es semejante a la teoría de divisibilidad de los Enteros, especialmente cuando los coeficientes se toman de un cuerpo.
Las Unidades y Asociados en un Anillo de Polinomios
[editar]Sea un anillo conmutativo con identidad. ¿Cuáles son las unidades, o sea los elementos con recíprocos, en el anillo de polinomios ? En general, la respuesta puede resultar complicada, como podemos apreciar del siguiente ejemplo.
Ejemplo.
Sea y consideremos los polinomios y Entonces, Es decir que es una unidad.
Como, usualmente, no esperamos que polinomios de grado positivo tengan recíprocos, lo anterior es una anomalía; la que eliminaremos si trabajamos con coeficientes en un dominio de integridad o como también diremos sobre un dominio de integridad, en particular, al trabajar sobre un cuerpo.
Proposición 1. Sea un dominio de integridad. Entonces, las unidades de coinciden con las unidades de
-
Demostración:
Sean y polinomios tales que Entonces, y deben ser polinomios de grado cero, ya que su producto tiene ese grado. Es decir que y con Por lo que concluimos que las unidades en son los polinomios de grado cero cuyos coeficientes son unidades del dominio de los coeficientes.
Cuando sea el anillo de los Enteros, las únicas unidades en son En cambio, si es un cuerpo, cualquier polinomio de grado cero no nulo es una unidad---que están identificados con los elementos no nulos del cuerpo.
Recordemos que decimos que dos elementos de un anillo está asociados cuando uno de ellos es un múltiplo por una unidad del otro.
Lema A. Sobre un cuerpo, cada polinomio tiene asociado un polinomio mónico.
-
Demostración: El polinomio que resulta al multiplicar el polinomio dado por el recíproco de su coeficiente líder es mónico.
Ejemplo.
Suponer Como y es un unidad, se tiene que es un asociado del polinomio original.
El Algoritmo de la División
[editar]En esta sección, veremos que tenemos un Algoritmo de la División para polinomios semejante al de los números enteros, siempre que el coeficiente líder del divisor sea una unidad del anillo.
Teorema. (El Algoritmo de la División).
Sea un anillo conmutativo con identidad. Sean y polinomios con coeficientes en tales que el coeficiente líder de sea una unidad de (o sea, invertible en ). Entonces, podemos hallar polinomios únicos y en tales que
-
Demostración: Primeramente, probaremos la existencia de los polinomios y
Si el grado de es cero, se tiene que donde es un elemento invertible de Entonces,
Lo que prueba la existencia, con y
(Existencia.) Supongamos, ahora, que el grado de es positivo. Si el grado de es menor que el grado de tendremos que:
lo que prueba la existencia con y
Supongamos, ahora, que el grado de fuera mayor o igual que el grado de Digamos que:
con y y invertible. Sea
| (1) |
Notemos que es igual a menos su término de mayor grado, por lo que tiene un grado inferior al de Suponiendo, por inducción, el resultado válido para todo polinomio de grado inferior a se tiene que podemos hallar polinomios y con y tal que
| (2) |
Sigue de (1) y (2) que Lo que finaliza la prueba la existencia.
(Unicidad.) Supongamos que con Entonces, Supongamos que Como el coeficiente líder de no es un divisor de cero, tenemos que
Mientras que por lo que obtenemos una contradicción. Luego, y, en consecuencia,
Nomenclatura. Llamamos dividendo y divisor a los polinomios y de la proposición anterior. Por su parte, los polinomios y se llaman el cociente y el residuo, respectivamente, de la división de por
Observación. Notemos que lo indicado en la demostración del caso cuando el grado del dividendo era mayor o igual al grado del divisor es el comienzo del proceso usual de división manual de polinomios, proceso que suponemos conocido del lector.
La Estructura del Anillo de Polinomios sobre un Cuerpo
[editar]En esta sección, veremos que la teoría de la divisibilidad en cuerpo, es totalmente análoga a la teoría de la divisibilidad en los Enteros.
Proposición 2. es DIP
Sea un cuerpo. Cada ideal de es principal. Los ideales no nulos tienen como generador a un polinomio con el menor grado entre los elementos del ideal.
(DIP significa dominio de ideales principales, todos los ideales son principales).
-
Demostración: Sea un ideal de Si Sea un ideal no nulo, por lo que habrá un polinomio no nulo en Seleccionemos en tal que su grado sea menor o igual a los grados de los otros polinomios no nulos en
Cuando el grado de es cero, se tiene que donde es un elemento de por lo que tiene recíproco. Luego es un elemento de y
Supongamos que el grado de es positivo. Sea cualquier polinomio en Por el algoritmo de la división, hay polinomios y con con nulo o con Se tiene entonces que
por lo que está en Como el grado de es minimal entre los polinomios no nulos de concluimos que Luego, cada elemento de es un múltiplo de o sea que está generado por
Como cada polinomio con coeficientes en un cuerpo tiene asociado un polinomio mónico, podemos siempre escoger como generador de un ideal en a un polinomio mónico.
Ejemplo.
La restricción de que los coeficientes pertenezcan a un cuerpo es necesaria. Veremos que no es un DIP.
Consideremos el ideal generado por el 2 y la indeterminada Los elementos de son todos de la forma No hay un polinomio que divida simultáneamente a 2 y a además 1 no está en Lo que muestra que es un ideal propio que no es principal.
MCD de Polinomios
[editar]Sean y dos polinomios. Si uno de ellos es nulo y el otro no, el polinomio no nulo es el mcd de ellos. Sean y polinomios no nulos. Consideremos el ideal generado por esos polinomios, Como es DIP, hay un polinomio de grado minimal que genera a Luego, para un par de polinomios Sigue de la relación anterior que cualquier divisor común de y es un divisor de Además, claramente, y están en por lo que son múltiplos de Luego, es el MCD buscado. Hemos probado la siguiente proposición.
Proposición 3. (MCD y Bezout para polinomios) Sean polinomios, no ambos nulos, en con cuerpo. Entonces, el ideal generado por y tiene como generador a un máximo común divisor de y que puede ser seleccionado mónico. Si es un se cumple la identidad de Bezout, o sea, hay polinomios y tales que
Como asociados de un mcd son mcd, siempre podemos escoger como EL mcd, al polinomio mónico asociado a un mcd.
Algoritmo para Computar el MCD
[editar]Hay un algoritmo, conocido como algoritmo de Euclides para obtener el MCD de dos polinomios.
El procedimiento (algoritmo) está basado en el siguiente resultado.
Proposición 4.
Sean y polinomios no nulos. Suponer que donde es el cociente de la división de por y es el residuo de esa división. Entonces, (excepto por una unidad),
-
Demostración: Sean y Consideremos la relación Sigue de la relación que cualquier divisor común de y es un divisor de por lo que será un divisor común de y ; aplicando lo anterior a tenemos que divide a Igualmente, la relación indicada implica que cualquier divisor común de y es un divisor común de y ; lo que implicará que divide a Por lo que y son asociados, luego, si son mónicos, son iguales.
Lo anterior sugiere un procedimiento para hallar el mcd de dos polinomios no nulos.
Notemos que como el residuo tiene un grado menor que el divisor, el proceso acaba en un número finito de pasos. El procedimiento se puede adoptar para generar los polinomios de la identidad de Bezout.
MCM de dos polinomios
[editar]Sean y dos polinomios no nulos. Cuando uno de ellos tiene grado cero, el otro es el MCM de los dos. Supongamos que los dos polinomios tienen grado positivo. Sean Como es un dominio de ideales principales, hay un polinomio mónico tal que Como está contenido en y en resulta que es un múltiplo común de e Además, cualquier múltiplo común de y estará tanto en como en por lo que estará en lo que implica que será un múltiplo de Luego,
Polinomios Irreducibles y Polinomios Primos
[editar]Recordemos las nociones de elementos irreducibles y primos en un dominio, pero aplicadas a polinomios.
Notemos que en cuerpo, cualquier polinomio de grado 1 es irreducible. Sin embargo, lo anterior no es cierto, inclusive sobre un dominio de integridad como los Enteros, como lo ilustra el siguiente ejemplo.
Ejemplo.
Sea El polinomio es irreducible en por lo que es irreducible en ya que es un unidad en o sea que está asociado con un irreducible. Sin embargo, no es irreducible en ya que 2 es un irreducible, por lo que es el producto de dos irreducibles de
Sabemos de un capítulo anterior que los elementos primos de un dominio son irreducibles. Veremos que para los polinomios sobre un cuerpo, los irreducibles son primos, por lo que no habrá diferencias entre esas dos clases de polinomios.
Proposición 5. Sea un cuerpo. Los polinomios irreducibles de son primos en
-
Demostración: Sea un polinomio irreducible y supongamos que Debemos probar que o Supongamos que Entonces, Sigue de la identidad de Bezout que hay polinomios tales que Multiplicando por tenemos que
Claramente, es un divisor del lado izquierdo en la última relación, ya que Luego, es un divisor de lo que prueba que es primo.
Cociente de k[X] por un irreducible
[editar]Sea un polinomio irreducible de con grado positivo y sea Sea tal que en Esto significa que no está en o sea que Por la identidad de Bezout, hay polinomios tales que
Pasando al cociente, tenemos que y como concluimos que Es decir que es invertible. Hemos probado, así, parte de la siguiente proposición.
Proposición 6. Sea un polinomio irreducible de con grado positivo mayor que 1. Entonces, es un cuerpo que contiene al cuerpo y a un cero de
-
Demostración: Los razonamientos anteriores al enunciado de la proposición, muestran que es un cuerpo.
Suponemos que mediante la identificación de elementos de con polinomios constantes (polinomios de grado cero o el polinomio nulo) Sea la función que envía de en su clase es la restricción a del supramorfismo canónico de en por lo que es un homomorfismo de anillos con identidad. Si se tiene que por lo que Por razones de grado, tenemos que lo que implica que es inyectiva, o sea que se trata de un monomorfismo que es, por lo tanto, un isomorfismo sobre su imagen. Usando el isomorfismo para identificar con su imagen, tenemos que por lo que es un cuerpo que contiene a
Sea en
Entonces, si pasando al cociente, se tiene que
lo que prueba que es un cero de
La Factorización Única en k[X]
[editar]El objetivo de esta sección es probar un teorema análogo al teorema fundamental de la Aritmética: "Cada entero positivo mayor que 1 es un producto de potencias de primos, tal que los primos y sus exponentes son únicos, excepto por el orden de aparición".
El siguiente resultado será necesario para el teorema deseado.
Lema B. Sea un cuerpo. Todo polinomio de grado positivo tiene un factor irreducible.
-
Demostración: Los polinomios de grado 1 son claramente irreducibles, por lo que el teorema se cumple para ellos, ya que cada polinomio es un divisor de si mismo.
Supongamos el resultado cierto para polinomios de grado a lo más Sea un polinomio de grado Si es irreducible, no hay nada más que probar. Si no es irreducible, entonces donde los grados de y de son inferiores al grado de pero mayores que 0. Por inducción, tiene un factor irreducible, que es también un factor de
Como cualquier asociado del factor de un polinomio es también un factor del polinomio, por lo que podemos escoger factores irreducibles que sean mónicos.
Teorema.(Factorización única).
Sea un cuerpo. Todo polinomio de grado positivo es el producto de una unidad por el producto único de potencias de irreducibles mónicos, diferentes entre ellos. La unicidad dice que los irreducibles que allí aparecen son únicos, así como las potencias a las que aparecen están unívocamente determinadas por excepto por el orden de aparición.
-
Demostración: (Existencia) Si es irreducible, no hay nada más que probar. En particular, polinomios de grado 1, Supongamos que la existencia fuera válida para polinomios de grado a lo más Sea un polinomio de grado Si es irreducible, es el producto de su coeficiente líder (unidad) por su asociado mónico. Si es irreducible, entonces donde Por inducción, y son productos de una unidad por potencias de irreducibles mónicos, luego su producto, también lo será, después de multiplicar las unidades y reagrupar potencias de irreducibles iguales.
(Unicidad) Supongamos que se tuviera que dos descomposiciones de un mismo polinomio. Digamos que
| (*) |
Consideremos al irreducible Como irreducibles son primos, es primo; por lo que es un divisor de Como eso implica que es un divisor de al menos uno de los factores de ese producto, se tiene que divide a uno de los Sin perdida de generalidad, podemos suponer que divide a (si no, cambiamos la notación). Luego, para algún polinomio pero como es irreducible, se tiene que debe ser una unidad. Luego, ambos polinomios tienen igual grado y como son mónicos, la unidad debe ser la identidad 1. Lo que implica que Cancelando factores iguales a en (*), se cancelarán todas las potencias de y Ya que si sobrará alguno de ellos en un lado, sería divisible por alguno de los irreducible del otro lado, pero esto implicaría que son iguales, lo que no puede ser. Si el resultado estaría probado. En caso contrario, procedemos como arriba, para ir eliminando factores iguales en ambos lados, hasta quedar
Ejercicios
[editar]El Teorema del Residuo y los Ceros de Polinomios
[editar]Las siguientes proposiciones nos ayudarán a determinar los ceros de en Tal determinación, como veremos es equivalente a determinar los factores lineales de
Proposición 7. (Teorema del Residuo) Sea un anillo conmutativo con identidad, un polinomio en Sea un elemento de El residuo de la división de por es exactamente
-
Demostración: Por el algoritmo de la división aplicado a (que tiene coeficiente líder invertible), obtenemos que
donde tiene grado menor que Por lo tanto, será un polinomio de grado cero o el polinomio nulo. Evaluando en obtendremos el resultado.
Corolario 7.1. (Teorema del Factor) Sea un anillo conmutativo con identidad, un polinomio de Un elemento de es un cero de ssi, es un factor de
-
Demostración: Por el algoritmo de la división, habrá polinomios y tales que:
Si es un cero de se tendrá que de donde y en consecuencia, será un factor de En forma recíproca, si es un factor de el residuo será nulo.
Ejemplo.
Sea en Como se tiene que es un factor de Dividiendo por obtenemos como cociente a Usando la fórmula cuadrática, obtenemos que ssi,
Lo que nos da los ceros adicionales y Por lo que tendremos que
Por lo que
Ejemplo.
Sea en Claramente 1 es un cero de por lo que tiene el factor Dividiendo por obtendremos como cociente Como
vemos que no tiene otro cero entero, de hecho ni siquiera reales. Luego, Sobre los Complejos,
Ejemplo.
Hallar los ceros de de
Resolución. Los cuerpos finitos, precisamente por su finitud y especialmente cuando la cantidad de elementos es pequeña, se prestan para evaluaciones exhaustivas de sus elementos. En este caso Luego,
Ceros Múltiples, Cantidad de Ceros
[editar]Observemos que cuando es un polinomio no nulo divisible por un polinomio mónico digamos que se tiene que no es un divisor de cero en A[X]. Por lo que tenemos que Luego,
Multiplicidad. Sea un cero de Sea el mayor entero positivo tal que En tal situación, decimos que es un cero múltiple con multiplicidad Sigue de la observación anterior que la multiplicidad es inferior al grado de Cuando la multiplicidad es 1, decimos que el cero es simple. Denotaremos por la multiplicidad de en el polinomio
En los polinomios sobre los Reales o los Complejos, un polinomio de grado tiene a lo más ceros. En general, lo anterior no es cierto, como lo muestra el siguiente ejemplo.
Ejemplo.
Sea y sea La tabla siguiente muestra la evaluación de en los elementos de
Luego, Sin embargo, no es igual o divisible por
Sin embargo, sobre un dominio de integridad, tenemos una situación análoga a aquella sobre los Reales y Complejos. Antes de probar lo anterior, probaremos el siguiente resultado.
Lema C. Sea un dominio de integridad y sean polinomios en Entonces,
-
Demostración: Claramente, Sea en entonces ; como estamos en un dominio, se tiene que o Es decir está en o en Luego
Proposición 8. Sea un dominio y un polinomio no nulo en Si entonces
donde es la multiplicidad de en y La cantidad de ceros de contando las multiplicidades es inferior o igual al grado de
-
Demostración: (Por inducción sobre el grado de )
Si el polinomio tiene grado 1, entonces debe ser 1 y por el teorema del factor.Supongamos que tiene grado mayor que 1 y que el resultado es válido para polinomios de grado inferior al de Sea uno cualquiera de los ceros, entonces
Por la hipótesis de inducción,
donde es la multiplicidad de en y Observemos que para cualquier cero de Por el lema, se tiene que y usando las relaciones para y anteriores se tiene que
De donde, se tiene que la suma de las multiplicidades debe ser inferior al grado de ya que estamos trabajando sobre un dominio.
Corolario. 8.1 (Cantidad de Ceros) En un dominio de integridad un polinomio de grado con coeficientes en el dominio tiene a lo más ceros en
Corolario 8.2. Sea un cuerpo con infinitos elementos y sean y polinomios con coeficientes en Entonces, como polinomios, ssi, son iguales como funciones.
-
Demostración: Si entonces para cada de se cumple que Por lo que y son iguales como funciones.
Supongamos, ahora, que y son polinomios tales que para cada en Sea Sigue de las hipótesis que para cada de Si es infinito se tiene que es un polinomio con infinitos ceros, que es mucho más de lo que puede tener un polinomio de grado Luego, el grado de es menor o igual a 0. Los polinomios de grado 0 no tienen ceros, por lo que la única posibilidad es el polinomio nulo, cuyo grado es menor que 0.
Derivadas y Ceros Múltiples
[editar]Para cada polinomio definiremos la noción de derivada de un polinomio. La derivada que definiremos proporciona el mismo resultado que la derivada de una función polinómica en los cursos de Cálculo. Esta noción de derivada, sin embargo, es formal y no requerirá de límites. La usaremos para determinar la existencia de ceros múltiples de un polinomio.
Definición. (Polinomio Derivado) Sea un polinomio de grado en Llamaremos polinomio derivado de al polinomio denotado por y definido por
La siguiente proposición muestra que los polinomios derivados tienen propiedades análogas a las derivadas de funciones.
Proposición 9. Sean y polinomios en un polinomio constante. Entonces, se tiene las siguientes propiedades:
-
Demostración: Las relaciones a) y b) siguen directamente de la definición.
Proposición 10. (Derivada y Multiplicidad). Sea un cuerpo y sea un polinomio de
-
Demostración:
Ejemplo.
Sea primo. Entonces, ya que el cuerpo tiene característica Es decir, que en esta situación, Lo que muestra la necesidad de la hipótesis de característica 0 en la proposición anterior.
Corolario 10.1. Sea un polinomio de Si hay un cero común a y entonces ese cero es al menos doble.
Corolario 10.2. En un cuerpo de característica cero, los polinomios irreducibles solamente tienen ceros simples.
-
Demostración: Sea un polinomio irreducible de grado Entonces, el coeficiente líder del polinomio derivado es y tiene un grado inferior a por lo que no hay polinomio de grado positivo que divida a y
Ejemplo.
Sea
Se tiene que Usaremos el algoritmo de Euclides para computar el mcd de y
Vemos que Es decir que es el mcd. Esto implica que hay un cero doble y que tal cero es precisamente
Expansión p(X)--aria de un Polinomio
[editar]Es conocido que dado un entero positivo cada número entero positivo se puede escribir de la forma
| (*) |
donde los 's son tales que La expresión en la derecha de (*) se llama la expansión --aria de
El resultado anterior es una consecuencia del algoritmo de la división. Como tal algoritmo es válido para polinomios en un cuerpo, tenemos, como consecuencia, un resultado análogo para los polinomios con coeficientes en un cuerpo.
Proposición 11. (Expansión --aria de un polinomio) Sea un cuerpo, un polinomio de grado positivo de Entonces, todo polinomio se puede escribir de la forma
| (**) |
donde los son polinomios en que son nulos o con grado inferior al grado de La expresión a la derecha de (**) se llama la expansión --aria de .
-
Demostración: Si es nulo o con grado 0, se tiene el resultado con y
Supongamos que es un polinomio de grado Por algoritmo de Euclides, tenemos que
| (1) |
donde y son polinomios en y tiene un grado inferior al grado de Se tiene entonces que grado de es inferior al grado de por lo que, por inducción, tenemos que
| (2) |
Sustituyendo este resultado en (1), obtenemos que
Poniendo, tenemos el resultado.
Corolario 11.1. Si cada uno de los es un elemento del cuerpo
Ejemplo.
Sea entonces
Cuando el cuerpo es de característica 0 se tiene el siguiente interesante resultado.
Proposición 12. (Teorema de Taylor) Sea un cuerpo de característica cero. Sea un elemento del cuerpo. Entonces, cada de grado en puede expandirse como
donde denota la --ésima derivada del polinomio evaluada en
-
Demostración: Ejercicio.
Ejemplo.
Sea el polinomio del ejemplo anterior y sea como en el ejemplo indicado. Entonces,
Lo que muestra como se produjeron los coeficientes de la expansión en el ejemplo anterior.
Este resultado se aplica en la descomposición en fracciones parciales de fracciones de polinomios con coeficientes en un cuerpo. Ver los ejercicios respectivos.
Ejercicios del Capítulo
[editar]19. La Factorización de Polinomios
[editar]Introducción
[editar]Este capítulo tiene como objetivo final el estudio de la factorización de polinomios con coeficientes en Enteros, los Racionales, los Reales y los Complejos.
Cuando se desarrolló la teoría para dicho estudio se observó que dependía de dos resultados:
Los resultados pueden generalizarse fácilmente al estudio de las relaciones entre la factorización de polinomios sobre dominios donde se tiene la propiedad de factorización única y la factorización de esos polinomios sobre el cuerpo de fracciones del dominio/
Este será el camino que seguiremos en las primeras secciones del capítulo. Posteriormente aplicaremos los resultados a la factorización sobre los cuerpos , y .
Veremos, también, los polinomios ciclotómicos que están relacionados con la factorización de , por su importancia en diferentes áreas de la matemática.
Finalmente, veremos una reseña del llamado Teorema Fundamental del Álgebra.
Los Dominios de Factorización Única
[editar]La siguiente definición singulariza a los dominios que tienen la propiedad de factorización única, tales como los Enteros y los anillos de polinomios sobre cuerpos.
Definición. (Dominio de Factorización Única, DFU) Decimos que un dominio es un dominio de factorización única, ssi, cada elemento no nulo que no sea una unidad se puede factorizar como un producto de elementos irreducibles de manera única.
.
Diremos que la expresión de un elemento en un producto de irreducibles es la descomposición del elemento en un producto de irreducibles. La unicidad de la descomposición significa que si tenemos dos descomposiciones del mismo elemento, digamos que
donde 's y 's son irreducibles, entonces se tiene que , y que cada es un asociado de , posiblemente después de una reenumeración de los irreducibles 's.
Los ejemplos básicos de DFUs son los Enteros: , y el anillo de polinomios , cuando es un cuerpo.
Se verifica que los dominios de ideales principales (DIPs) son siempre DFUs. El lector interesado puede examinar lo hecho en el caso de los polinomios sobre un cuerpo para intentar la demostración de esa afirmación.
Una consecuencia de la descomposición única en producto de irreducibles es que dos elementos, no ambos nulos, siempre tienen mcd y mcm.
Proposición 1. En un DFU, dos elementos no nulos tienen MCD y MCM.
-
Demostración: (La demostración es el proceso usual para calcular el mcd y el mcm de dos números enteros cuando se conoce sus factorizaciones en números primos.) Sean y dos elementos no nulos de . Sean la reunión de los irreducibles que aparecen en la descomposición de con los irreducibles que aparecen en la descomposición de . Entonces, podemos poner que
donde los 's y 's pueden ser positivos o cero (cero cuando el irreducible no aparecía en la descomposición en irreducibles del elemento). Sea , . Entonces, es un mcd de y . Análogamente, pero usando el mayor exponente en cada descomposición, obtenemos un mcm. Dejaremos al cuidado de lector la verificación de lo anterior.
Otra consecuencia importante de la descomposición única es la siguiente proposición.
Proposición 2. En un DFU, los irreducibles son primos.
-
Demostración: Supongamos que es un irreducible tal que . Debemos probar que o . Si no hay nada más que probar. Supongamos que y que es tal que (*). Como es un factor de la izquierda en (*), por la unicidad de la descomposición, debe aparecer en la descomposición en irreducibles del lado derecho de (*). Como de be aparecer en la descomposición en irreducibles de . En consecuencia, .
Un estudios más detallado de los DFUs, se hallará en el capítulo Tipos de Dominio.
Polinomios sobre Dominios de Factorización Única
[editar]El principal objetivo de esta sección será generalizar relaciones entre polinomios en y polinomios en , a polinomios sobre -- un DFU---y polinomios sobre , donde es el cuerpo de fracciones de . Comenzaremos generalizando una propiedad de los polinomios con coeficientes enteros, llamada en ese contexto, el teorema de los ceros racionales}.
Proposición 3. (Teorema de los Ceros Racionales de Descartes) Sea un DFU y sea su cuerpo de fracciones. Sea un polinomio de grado en , entonces si con y en y con su mcd igual a 1, es un cero de , se cumple que y que .
-
Demostración: Como es un cero de en , tendremos (en ) que
De donde, multiplicando por , tendremos que:
En la igualdad anterior, divide de manera obvia cada uno de los sumandos, excepto a lo más el último. Como, también, divide trivialmente al segundo miembro, concluimos que debe dividir al mencionado sumando. Es decir, ; pero como , concluimos que .
Razonando de manera análoga con , se concluye el otro resultado.
Corolario 2.1. Sea un DFU y su cuerpo de fracciones. Sea mónico. Cualquier cero en de es un elemento de .
-
Demostración: Sigue del teorema que si es una solución, divide al
coeficiente líder del polinomio; como dicho coeficiente es 1, se concluye que es una unidad, por lo que su recíproco está en . Es decir que está en .
Recordemos que llamamos número algebraico a cualquier número complejo que es un cero de un polinomio con coeficientes enteros. Cuando el polinomio es mónico, decimos que se trata de un entero algebraico. Sigue del corolario anterior que,
Corolario 2.2.
Si es un entero algebraico que es un número racional, se tiene que es un entero ordinario (o sea un elemento de ).
El resultado anterior tiene, entre sus aplicaciones, la demostración de la irracionalidad de algunos números.
Ejemplo.
Probar que es irracional.
Resolución> Busquemos un polinomio que tenga a como un cero.
Luego, es un cero del polinomio mónico que es un polinomio en . Si fuera racional, sería (por el corolario) un número entero . Por la proposición, . Luego, . Pero, y , por lo que no puede ser entero. Hemos llegado a una contradicción que implica que no es racional.
Convenio. En el resto de esta sección, supondremos que es un DFU y que es su cuerpo de fracciones.
Estudiaremos, a continuación, la relación entre los irreducibles de y aquellos de . Para ese estudio, introduciremos la noción de polinomio primitivo que resultara fundamental.
Definición. (Polinomio Primitivo) Sea un DFU. Diremos que un polinomio en es primitivo, ssi, un máximo común divisor de sus coeficientes es una unidad.
Lema A. Sea un DFU. Sea un polinomio en y sea el mcd de sus coeficientes. Entonces donde es primitivo. Además, dicha descomposición es única, excepto por asociados. Es decir, si donde y son elementos de y y son polinomios primitivos, entonces se debe cumplir que y son asociados en , y que y son asociados en .
-
Demostración: La existencia es inmediata, basta con factorizar el mcd de los coeficientes. Supongamos que como en las hipótesis. Como , se ve que y son máximos común divisores de los coeficientes de ,por lo que y son asociados. Digamos que con
unidad. Sustituyendo en la relación anterior, , se ve que y son asociados.
Proposición 4. (Lema de Gauss) El producto de dos polinomios primitivos es primitivo.
-
Demostración: Sean y dos polinomios primitivos y sea . Queremos probar que es primitivo. Sean
Supongamos que hubiera un irreducible en , que dividiera a todos los coeficientes de . En particular, dividiría a , por lo que dividiría a o a . Supongamos que dividiera a . Como y son primitivos, no puede dividir a todos los coeficientes de ni a todos los coeficientes de . Sea el menor coeficiente de tal que y sea el menor coeficiente de tal que . Notemos que , mientras que . Veamos el coeficiente de del producto. Se trata de
Observemos que divide la primera expresión entre paréntesis, ya que divide cada uno de los 's que allí aparece. Igualmente, divide a cada uno de los 's que aparecen en la segunda expresión entre paréntesis. Pero, no divide a . Por lo que no divide a todos los coeficientes del producto. Luego, dicho producto debe ser primitivo.
La siguiente proposición es la proposición central para nuestros efectos.
Proposición 5. Sea un DFU y sea su cuerpo de fracciones Sea un polinomio primitivo en con grado mayor o igual que 1. Entonces es reducible en , ssi, es reducible en .
-
Demostración: Como puede considerarse como un subanillo de , podemos también considerar a como un subanillo de .
Supongamos que fuera reducible en , digamos que
{{Eqn}|1}}
donde ni ni son unidades.
Si , entonces donde es un elemento de . Entonces , pero como es primitivo, sería una unidad, por lo que sería una unidad. Luego . Análogamente, .
Como, es un subanillo de , la ecuación (1) es válida en , y ni ni pueden ser unidades en , por lo que es reducible en .
Recíprocamente, sea un polinomio primitivo en que es reducible en , digamos que en , con grados de y mayores o iguales que 1 y con coeficientes en . Escribamos todos los coeficientes de y de modo que las fracciones en los coeficientes tengan un denominador común, digamos .
Entonces
| (2) |
donde y son polinomios en . Sea el producto del mcd de los coeficientes de y . Entonces,
| (3) |
donde , pero y , son polinomios primitivos en .
Como el lado izquierdo es un polinomio en , se tiene que el polinomio de la derecha es también un polinomio en , por lo que debe ser un factor de todos los coeficientes de y de todos los de . Como esos polinomios son primitivos, se debe cumplir que es una unidad de , digamos que hay un en tal que . Luego,
| (4) |
Como es primitivo, cualquier común divisor de sus coeficientes es una unidad en . Como a la derecha el máximo común divisor de los coeficientes es multiplicado por una unidad, se tiene que es un mcd de los coeficientes de , por lo que debe ser una unidad en . Luego, la ecuación (4) es una igualdad en , que prueba que es reducible.
Ejemplo.
Consideremos el polinomio de . ¿Es reducible como polinomio de ?
Resolución. Si lo fuera, lo sería, por la proposición anterior, también en , donde se tendría que
con y enteros cuya suma debería ser igual a 14 y cuyo producto sería igual a 6. Como, claramente, tales números no existen, concluimos que es irreducible en .
El siguiente corolario a la proposición anterior es clave para la demostración de que es DFU cuando lo es.
Corolario 5.1. Sea un DFU. Los polinomios irreducibles de son polinomios primos.
-
Demostración: Sea un polinomio irreducible de . Probaremos, primeramente, que es primitivo. Por el Lema A se tiene que donde es primitivo. Si no fuera unidad, tendríamos que lo anterior sería una factorización de tal que ninguno de los factores es una unidad. Luego, es una unidad. Esto implica, que y son asociados, por lo que concluimos que es un polinomio primitivo.
Si el grado de fuera 0, tendríamos que es un elemento de y, en un DFU los irreducibles son primos, por lo que sería un elemento primo de . Probaremos, que también es primo en . Supongamos que . Usando el lema citado, podemos escribir
donde y son elementos de y y son polinomios primitivos. Por el lema de Gauss, es también primitivo. Por lo que la única manera que es que , Pero como, irreducibles son primos en , se debe tener que o . Por lo que, o , o sea que se trata de un primo en .
Supongamos ahora que el grado de es positivo y que . Debemos probar que o . Sea el cuerpo de fracciones de y la relación en . Por la proposición, continúa siendo irreducible en ; como es un DFU, tenemos que es primo en . Luego, o . Supongamos que . Es decir que hay un en tal que
| (1) |
Se tiene que podemos escribir como
| (2) |
Donde es un polinomio primitivo en y , son elementos de con . Luego
| (3) |
El producto es un polinomio primitivo, ya que es un producto de polinomios primitivos. Como es un polinomio con coeficientes en , cada coeficiente de debe ser divisible por . Luego, es una unidad de y está en . Luego, la ecuación (3) muestra que divide a en .
Teorema A. Si es un DFU, entonces es un DFU.
- Demostración: Sea un polinomio no nulo, debemos probar que es un producto de irreducibles esencialmente de una única manera---o sea, excepto por factores que sean unidades. La prueba es por inducción sobre el grado de .
Si el grado de es cero, entonces es un elemento de . Si fuera reducible en lo sería en . Es decir que elementos irreducibles de permanecen irreducibles en . Como es un DFU, tiene una factorización única en términos de irreducibles.
Supongamos que el grado de fuera y supongamos el resultado válido para todos los polinomios con grado inferior a . Si es irreducible, no hay nada más que probar. Supongamos que fuera reducible, entonces,
Por la hipótesis de inducción, se tiene que y tienen una descomposición en irreducibles. Por lo que su producto, también la tiene.
Para probar la unicidad, se razona como en la proposición correspondiente en el caso de los polinomios. Es decir, usando que irreducibles son primos, y cancelando los primos asociados en ambas descomposiciones.
Corolario A.1.
es un DFU.
El Criterio de Eisenstein
[editar]Hay un criterio muy útil para saber si un polinomio es irreducible en y, por lo tanto, en , donde es el cuerpo de fracciones de .
Proposición 6. (Criterio de Eisenstein) Sea un DFU. Sea en
Si hay un primo en tal que cuando , y , entonces es irreducible en (y, pot lo tanto, en ).
-
Demostración: Si no es un polinomio primitivo, podemos tomar un máximo común divisor de sus elementos, digamos y poner
, donde es un polinomio primitivo en . Notemos que como polinomios en , y son asociados. Sea un primo que satisface las hipótesis para . Como , tenemos que . Luego, si es el coeficiente del término de grado , tenemos que , ssi, , para . Análogamente, las otras condiciones se cumplen para . Por lo que, sin perdida de generalidad, podemos suponer que el polinomio del enunciado del teorema es primitivo en . Por la proposición 5 basta con probar que es irreducible en . Supongamos que, al contrario, en se cumple que
Por los hipótesis, tenemos que , por lo que o . Sin perdida de generalidad, podemos suponer que . Entonces, ya que . Notemos que no puede dividir todos los coeficientes de , ya que pues . Luego, hay un tal que , pero . Además, . Examinemos el coeficiente de .
Sabemos por hipótesis que . Por definición de , divide todos los sumandos con . Luego, . Como , se debe cumplir que . Pero esto contradice, la elección de . Hemos llegado a una contradicción, lo que prueba que es irreducible en .
Ejemplos.
Ejercicios
[editar]Factorización sobre los Racionales
[editar]La factorización sobre usa todos los resultados anteriores más algunas manipulaciones interesantes. En primer lugar, observemos que si es un polinomio en y es igual al mcm de los denominadores de sus coeficientes, entonces
, donde es un polinomio en . Si resultara que fuera primitivo, tendríamos que sus factores irreducibles en serían iguales a sus factores en , ver la proposición 5. Por lo que, en principio, basta considerar polinomios primitivos en . Como los polinomios mónicos son ciertamente primitivos, veremos a continuación un truco para convertir un polinomio en un polinomio mónico, cuya factorización se refleja en la factorización del polinomio original. Comenzaremos con un ejemplo de factorización, que recuerda un truco de la escuela secundaria.
Ejemplo.
Factorizar .
Resolución. Sea , entonces . Sea . Entonces, , o sea un polinomio mónico. Por inspección es fácil ver que . Por lo que
. Como , tenemos que .
Notemos, la sustitución que ayuda en la factorización anterior.
Lo hecho en el ejemplo anterior es totalmente general. En efecto, sea , . Si entonces es mónico. Supongamos que . Sea . Tenemos que
Poniendo, , se tiene que . Es decir que es mónico como polinomio en la indeterminada .
Proposición 7. Sean y como en la discusión anterior. Entonces, es irreducible, ssi, es irreducible.
-
Demostración: Si fuera una factorización propia de . Entonces, . Análogamente, si fuera reducible.
La demostración muestra que cualquier factor irreducible de lo es de y viceversa. Es decir, que podemos factorizar el polinomio mónico, para obtener la factorización del polinomio general.
Ejemplo.
Factorizar .
Resolución. Sea , con .
Por el teorema de los ceros racionales, los únicos ceros posibles enteros son los divisores de 12: , , , , y . Evaluando tenemos que
Por lo que es un cero y, por lo tanto, es un factor de ; o, equivalentemente es un factor de . Notemos que como el grado de y es 3, podemos hallar los otros posibles ceros, hallando primeramente el cociente entre y .
Usando el resultado del ejemplo siguiente a la proposición 6,el cociente es un polinomio irreducible sobre . Luego,
Criterio de Irreducibilidad: reducción módulo m
[editar]Además del criterio de Eisenstein, hay un método relativamente simple de verificar si un polinomio en es irreducible. Ilustraremos el método con un ejemplo.
Ejemplo.
Probar que es irreducible sobre .
Resolución. Considerando el polinomio como un polinomio sobre , vemos que , es decir que no tiene ceros sobre , por lo que no es factorizable sobre . La conclusión es que no puede serlo sobre , por lo que discutiremos a continuación.
Sea en , tal que . Sea un número entero y definamos como la reducción módulo de los coeficientes de , es decir que . Por ejemplo,
. Notemos que dicho polinomio es, por evaluación en 0 y 1, irreducible en . La siguiente proposición muestra que es irreducible en .
Notemos que si es mónico, también lo será y, entonces, los grados de ambos polinomios son iguales.
Proposición 8. Sea un polinomio mónico en . Si para algún entero , es irreducible en , entonces es irreducible en ; donde es la reducción de los coeficientes módulo .
La demostración sigue del siguiente lema cuya demostración dejaremos de ejercicio.
Lema B. Sea un polinomio mónico en . Si en entonces .
-
Demostración de la proposición: Directo del lema, ya que si es reducible sobre , su reducción módulo también lo será, para todo .
Ejemplo.
Sea . Entonces, . Ese polinomio es reducible en , ya que . Sin embargo, es tal que , por lo que es irreducible en . Luego, el polinomio es irreducible en .
Ejercicios
[editar]Los Polinomios Ciclotómicos
[editar]Consideremos al polinomio de . Los ceros complejos de se llaman las raíces enésimas de la unidad. Sabemos de trabajos anteriores que tales raíces forman un subgrupo multiplicativo de que denotamos por . El grupo es cíclico y de orden .
Decimos que una raíz enésima es una raíz enésima primitiva de la unidad, ssi, es un generador de .
Se sabe que es una raíz primitiva de la unidad, por lo que
Se tiene que es primitiva, ssi, .
La notación resulta muy conveniente en este contexto, porque permite usando propiedades de potencias escribir resultados de forma compacta. La siguiente proposición muestra algunas propiedades de esa notación, que está conectada con la llamada representación polar de los complejos.
Proposición 9. (Propiedades de )
-
Demostración: Ejercicio.
Definición. (Polinomio Ciclotómico Enésimo) Sea un entero positivo y sea una de las raíces primitivas de . Llamamos enésimo polinomio ciclotómico al polinomio en .
Observemos, primeramente que el grado de es donde es la función de Euler.
Los primeros polinomios ciclotómicos son:
Notemos que cada uno de los polinomios anteriores tienen coeficientes enteros. Esto es válido en general.
Proposición 10. Sea . Entonces,
-
Demostración:
Corolario 10.1. ,
-
Demostración: Calculando grados en la igualdad de la parte a).
Ejemplo.
Hallar .
Resolución. Se tiene que . Despejando, tenemos que
Ejercicios
[editar]El Teorema Fundamental del Álgebra
[editar]Discutiremos en esta sección, la factorización de polinomios con coeficientes en los Complejos, que tiene entonces como casos especiales los casos con coeficientes en y en .
Vimos en la sección pasada que la factorización en puede reducirse a la factorización en . Hay, además, algoritmos debidos a Lagrange (no muy efectivo) y a Berlekamp (bastante eficiente) para la factorización para polinomios con coeficientes enteros. Al contrario, para polinomios arbitrarios con coeficientes reales o complejos no hay tales algoritmos. Hay, sin embargo, fórmulas para la resolución de ecuaciones de segundo, tercer y cuarto grado, que permiten factorizar polinomios de grado inferior a 5. La búsqueda de ceros de polinomios cualesquiera en puede hacerse en forma aproximada mediante algoritmos, siendo uno de los más eficientes aquel de Newton--Raphson que aparece en los cursos de Cálculo.
En los aspectos teóricos, la experiencia en la resolución de ecuaciones llevó a conjeturar que
La primera conjetura se conoce como el teorema fundamental del Álgebra, y pruebas relativamente completas de ese resultado empezaron a aparecer a partir de 1801 (Gauss). Formalmente, el resultado es
Teorema Fundamental del Álgebra Cada polinomio en de grado positivo tiene al menos un cero en .
La demostración del teorema escapa el alcance de este libro por lo que referiremos a la literatura para la misma. Usualmente aparece en libros de Análisis sobre los Complejos y, también, en textos más avanzados de Álgebra, por ejemplo, mirar en [5].
Sigue del teorema que cualquier polinomio en de grado factoriza en exactamente factores lineales (con posibles repeticiones). En particular, todos los polinomios con coeficientes racionales o reales factoriza en factores lineales sobre ,
Ejemplo.
En un ejemplo anterior vimos que factoriza sobre como . Usando la fórmula cuadrática, vemos que , ssi,
Si y entonces
Usaremos el teorema fundamental para probar la segunda conjetura mencionada.
Proposición 11. No hay polinomios irreducibles de grado mayor que en ,
-
Demostración: Sea un polinomio de grado mayor que 2 de . Si tiene un cero en , entonces, como sabemos, es reducible.
Supongamos que no tiene ceros reales. Por el teorema fundamental tiene al menos un cero complejo, digamos .
Sea . Si , entonces y
Como no tiene ceros reales es irreducible sobre .
Dividiendo por en , obtendremos un cociente y un residuo tal que , donde el grado de es a lo más 1, digamos que , con y en . Evaluando (1) en se tiene que
Como es un cero de y concluimos que . Pero, esto implica que (ver ejercicio \ref{ex100401}). Luego, , y, por lo tanto, divide a . Es decir que es reducible.
Observación. El tema de los ceros de polinomios con coeficientes reales es un viejo tema. Algunos de los primeros resultados incluyen un teorema (la Regla de Descartes) sobre la cantidad de soluciones positivas y negativas de una ecuación polinómica. Hay otro teorema (algoritmo de Sturm) que permite computar la cantidad de ceros entre dos números dados. Como dijimos anteriormente, cuando se desea factorizar un polinomio real, lo usual es usar métodos aproximados. El lector debe buscar un libro sobre Análisis Numérico para ver acerca de dichos métodos.
Ejercicios
[editar]Notas
[editar]20. Las Extensiones de Cuerpos
[editar]Introducción
[editar]Los Cuerpos son la estructura más completa en término de operaciones. Representan el dominio natural donde estudiar las cuatro ``operaciones aritméticas tradicionales. El Álgebra, hasta el siglo XIX, fue principalmente el estudio de las ecuaciones polinómicas, especialmente sobre los Reales y Complejos. El siglo XIX se inicia, matemáticamente, con las primeras demostraciones más o menos completas del llamado ``teorema fundamental del álgebra (cada polinomio con coeficientes complejos tiene un cero complejo). Los trabajos de Lagrange, Ruffini, Abel y Galois, completan los trabajos de siglos anteriores, iniciando al mismo tiempo una nueva visión del álgebra que llevaría en alrededor de cien años a lo que actualmente concebimos como álgebra abstracta. \medskip Los Complejos se obtienen de los Reales agregando (técnicamente, adjuntando) el número cuyo cuadrado será igual a . Se extiende las operaciones de suma y multiplicación y se obtiene una estructura de cuerpo en los Complejos. Desde el punto de vista de las ecuaciones, tenemos un cero para el polinomio , que era irreducible sobre los Reales--es decir sin ceros reales.
La primera parte de este capítulo está dedicado a la generalización de la construcción de los Complejos, aplicados a un cuerpo cualquiera y a un polinomio irreducible cualquiera. Luego, veremos la relación entre subcuerpos y grupos de automorfismos, que es el aspecto central de la teoría de Galois (Proposición 10). Finalmente, estudiaremos los cuerpos finitos, que además de su importancia en el desarrollo de la teoría, tienen actualmente muchas aplicaciones.
\medskip Recordemos que decimos que un cuerpo es una extensión de un cuerpo , ssi, es un subcuerpo de . Cuando es un extensión de y es un cuerpo tal que , decimos que es un cuerpo intermedio entre y .
Ejemplo.
El cuerpo es una extensión de . es un cuerpo intermedio entre y .
La Adjunción de un Elemento
[editar]Sean una extensión del cuerpo . Sea un elemento de . Nos interesa, ahora, determinar el subcuerpo más pequeño de que contiene a y a . Cuando dicho subcuerpo exista, diremos que se ha obtenido por adjunción de a y lo denotaremos por , Tal cuerpo será intermedio entre y .
Ejemplo.
Consideremos al cuerpo como una extensión del cuerpo y al elemento . ¿Cuál será el subcuerpo más pequeño de que contenga a y a ?
Supongamos que tal subcuerpo existe y que lo denotamos por . En primer lugar, tenemos que debe contener a todos los números racionales y, en segundo lugar, a (usaremos en lugar de , para destacar la validez del proceso siguiente para un número irracional cualquiera). Como es cerrado respecto a la multiplicación, tendremos que todas las potencias naturales positivas de serán elementos de . En particular, cuando sea un número entero positivo cualquiera, tendremos, para cualquier número racional , que es un elemento de . También, las sumas de elementos de la forma anterior serán elementos de . Por lo que los polinomios en serán también elementos de . Como se trata de un cuerpo, los cocientes de tales polinomios serán elementos de .
Usando las reglas de las operaciones con fracciones, vemos que el conjunto formado por tales fracciones tiene la estructura algebraica de un cuerpo. Además, ese cuerpo contiene a los Racionales y a , es decir que debe contener al cuerpo . Por otra parte, cualquier cuerpo que contenga a y debe contener cada una de esas expresiones. Por lo que concluimos que la "menor" extensión de que contiene a está formada por las fracciones de expresiones polinómicas en .El proceso descrito es general, por lo que tenemos la siguiente proposición.
Proposición 1. (Adjunción de un elemento) Sea un cuerpo cualquiera, un elemento de una extensión de . Entonces, el subcuerpo de obtenido adjuntando a , , consiste de todos las fracciones de expresiones polinómicas en con coeficientes en . Dicho cuerpo está contenido en cualquier otro subcuerpo de que contenga a y a .
- Demostración: Ejercicio.
La Adjunción de Elementos Algebraicos
[editar]En esta sección, iniciaremos el estudio de la estructura de las adjunciones de elementos que son ceros de polinomios. Tales elementos reciben un nombre especial que extienden a un contexto general la noción de número algebraico vista anteriormente.
Definición. (Elemento Algebraico) Sea una extensión del cuerpo . Diremos que un elemento de es algebraico sobre , ssi, hay un polinomio con coeficientes en , tal que .
Cuando , recordemos que llamamos números algebraicos a los elementos de que eran, de acuerdo a la definición anterior, algebraicos sobre .
Ejemplos.
Notemos que cuando un elemento sea algebraico sobre un cuerpo, lo será también sobre cualquier extensión del mismo. El resultado converso no es cierto.
En primer lugar, ilustraremos, con un ejemplo, algunas de las peculiaridades que tienen las adjunciones por elementos algebraicos. En una sección posterior, generalizaremos dicho ejemplo a una construcción precisa de una extensión por adjunción de un elemento algebraico.
Ejemplo.
Sean y . Sea un número entero que no es un cuadrado perfecto en . Entonces, los ceros de son números algebraicos que no son racionales, ya que si lo fueran deberían ser enteros. El polinomio será, por lo tanto, irreducible sobre . Sea uno de sus ceros complejos, entonces . Queremos precisar la forma de los elementos de , que por un resultado anterior, son fracciones de polinomios en . Observemos que implica que:
Los ejemplos sugieren que para todo entero mayor que 2, se cumple que es igual a un racional o al producto de un racional por . Lo anterior, se puede verificar fácilmente por inducción, lo que dejaremos al cuidado del lector.
El resultado anterior implica que cualquier expresión polinómica en será igual, por reagrupación de términos con igual potencia de , a una expresión de la forma , con , elementos de .
Por lo tanto, los elementos de serán, de acuerdo con la proposición 1, fracciones de la forma
con , , y en .
Observemos, a continuación, que en , para todo y en se tiene que:
por lo que podremos simplificar aún más las expresiones de los elementos de . En efecto, tendremos que:
Ejercicios
[editar]Congruencias Módulo un Polinomio
[editar]En la sección anterior, iniciamos el estudio de la estructura que resulta al adjuntar un elemento algebraico a un cuerpo. En nuestros ejemplos siempre supusimos la existencia de una extensión del cuerpo donde vivía el elemento algebraico. Pero, cuando queremos solucionar una ecuación no siempre sabremos si tal solución existe y, parte del trabajo. será determinar si tal solución existe. En esta sección, trataremos de responder a esa pregunta, la que formularemos explícitamente como un problema.
Sea un cuerpo y un polinomio en , ¿cuáles serán los ceros de y adónde estarán? O de manera equivalente, ¿habrá una extensión de que contenga al menos un cero del polinomio ?
En primer lugar, observemos que si , cualquier cero de uno de los factores de es también un cero de , por lo que podemos reducir nuestras consideraciones a polinomios irreducibles que además, sin perdida de generalidad, podremos suponer mónicos. Además, como los ceros de polinomios de de grado 1, son elementos de , supondremos que el grado del polinomio es mayor que 1.
La construcción seguirá como ejemplo la construcción de a partir de . Primeramente, usaremos las analogías algebraicas entre el anillo de los Enteros y el anillo de polinomios sobre un cuerpo para extender la noción de congruencia de los números enteros al anillo de los polinomios.
Definición. (Congruencia de Polinomios) Sea un cuerpo cualquiera y sea un polinomio de grado positivo en . Decimos que dos polinomios y son congruentes módulo y escribimos
ssi, es un múltiplo de .
La relación de congruencia anterior tiene propiedades semejantes a la congruencia de números enteros. Por ejemplo, es una relación de equivalencia (¡verificarlo!). Por lo que particiona a en clases de equivalencia. Recordemos que cuando sea un polinomio, su clase de equivalencia (respecto a la relación de congruencia) estará dada por
Recordemos que las clases de equivalencia siempre son disjuntas entre si y que su reunión es todo el conjunto.
La siguiente proposición proporciona, varios enunciados equivalentes a la noción de congruencia anterior.
Proposición 2. Sea un cuerpo y un polinomio de grado positivo de . Las siguientes afirmaciones son equivalentes:
-
Demostración: Ejercicio.
Sean y como arriba y sea el ideal generado por en . Si y son polinomios congruentes módulo , entonces es un elemento de . Viceversa, cuando la diferencia de dos polinomios esté en , dicha diferencia será un múltiplo de . Es decir que las clases de congruencia módulo coinciden con los elementos del anillo cociente .
Estructura de .
Sean cuerpo y un polinomio de grado positivo en . Sea un polinomio cualquiera de . Entonces, por el algoritmo de la división, podemos hallar polinomios y tales que y . Por lo que es un múltiplo de . Es decir que
-
Cada polinomio de es congruente módulo a un polinomio de grado inferior al grado de .
Por lo que, siempre, podremos escoger representantes de las clases de congruencia a polinomios cuyo grado sea inferior al grado de . Además, dos polinomios diferentes con grados inferiores a deben pertenecer a clases diferentes, ya que su diferencia será menor al grado de , por lo que dicha diferencia no puede ser un múltiplo de . Los polinomios de grado 0 pueden identificarse con los elementos de . Por lo que la clase de equivalencia de en será mismo.
Se tiene la siguiente proposición.
Proposición 3. Sea un cuerpo y sea un polinomio en de grado . Entonces, el anillo cociente está formado por las clases de equivalencia de polinomios en con grado a lo más . Dicho anillo contiene una copia isomorfa a formada por las clases de los polinomios constantes y el polinomio nulo.
-
Demostración: Sigue de los razonamientos anteriores que cada clase de congruencia tiene un representante que es un polinomio de grado a lo más . Además, dos polinomios diferentes de ese tipo están en clases diferentes. Sea un polinomio de grado inferior a . Pasando al cociente, tenemos que
La siguiente proposición es el objetivo de nuestra exploración
Proposición 4. (Existencia de Extensión y Cero) Sea un cuerpo y un polinomio irreducible en . Entonces, es una extensión de --cuerpo que contiene a . Además, la clase es un cero del polinomio .
-
Demostración: Como el polinomio es irreducible, el polinomio es primo, por lo que sabemos que es un dominio; probaremos que es un cuerpo. Sea en . Entonces, no está en , lo que implica que . Como es irreducible, eso significa que . Por la identidad de Bezout, hay polinomios y tales que . Pasando al cociente, tenemos que
Como , se tiene que , lo que prueba que es invertible y que, en consecuencia, es un cuerpo. Sigue de la proposición anterior que es una extensión de --identificado con las clases de los polinomios de grado 0 y del polinomio nulo. Finalmente, como la clase de es igual a cero, se tiene que , lo que muestra que es un cero de .
Corolario 4.1. (Existencia de Extensiones) Sea un cuerpo y sea cualquier polinomio de . Entonces, hay una extensión de que contiene un cero de .
- Demostración: Sea un factor irreducible de . Entonces, por la proposición anterior, el cuerpo es una extensión de que contiene un cero de . Como cualquier cero de es un cero de , se tiene el resultado.
La construcción anterior de una extensión del cuerpo para obtener un cero de un polinomio de , fue inventada por el matemático alemán Leopold Kronecker (1823--1891).
Ejemplo.
Sea y .
Por inspección, vemos que no tiene ceros en , por lo que es irreducible sobre . Luego, es un cuerpo que es un extensión de .
Las clases de equivalencias de son , , y .
Como , tenemos que . Es decir que es un cero de . Luego, (se trata de un anillo con característica 2). Luego, .
Sea la clase de en . Se deja de ejercicio verificar las siguientes tablas de operaciones en .
Ejemplo.
Ejemplo.
Consideremos el cuerpo y sea . ¿Tiene ceros? ¿Cuántos ceros?
En primer lugar, observemos que la ecuación no tiene soluciones en , ya que los cuadrados en son , y . Por lo tanto, el polinomio dado es irreducible. Por la teoría general de los ceros de un polinomio sobre un cuerpo, sabemos que tiene a lo más dos ceros. Notemos que si podemos hallar alguna solución, en algún lugar, podríamos llamar a esa solución y, entonces, la otra solución sería , por lo que también estaría en la misma extensión.
Un cuerpo que contiene a y contiene las dos soluciones es
Los ejemplos anteriores muestran situaciones en donde la construcción de un cuerpo que tiene al menos un cero de un polinomio, nos conduce a un cuerpo donde están todos los ceros del cuerpo. Lo anterior, se debe a que el polinomio escogido tenía grado 2. En general, lo anterior no es cierto, como veremos en el próximo ejemplo.
Ejemplo.
Sea y sea . Claramente, se tiene que es irreducible sobre . De ser reducible, tendría necesariamente, un factor de grado 1. Aplicando el teorema de los ceros racionales, ya que el polinomio es mónico, dicho cero debería ser entero y, claramente no hay entero cuyo cubo sea igual a 2.
Sea . Sabemos, por nuestros trabajos que estaría formado por todos los números de la forma
con , y números racionales. Por lo que todos esos números serían números reales.
Por otra parte, sabemos de nuestros trabajos con los números complejos que las soluciones de la ecuación son los números complejos: , , y , donde es una de las raíces cúbicas primitivas de .El ejemplo anterior muestra que la construcción o la adjunción de un cero de un polinomio irreducible a , puede producir un cuerpo que no necesariamente contiene a todos los ceros del polinomio. Los resultados anteriores garantizan tan sólo la existencia de una extensión que contiene, por lo menos, un cero; pero, como muestra el último ejemplo, puede que ese sea el único cero que contenga.
Veremos, a continuación, como obtener una extensión que contenga todos los ceros de un polinomio dado.
Sean cuerpo y un polinomio irreducible sobre . Sea la extensión de donde tiene al menos la solución . Por la teoría general de polinomios, se tendrá que, será un factor de en , o sea que habrá un polinomio en tal que:
Si tiene algún factor lineal, dicho factor nos produce otra solución en . Ver ejemplo discutido arriba. Supongamos que podemos factorizar sobre como , donde puede ser un elemento de o un irreducible sobre y puede ser cero. Con , queremos decir que . La descomposición anterior implica que los ceros de que están en son: y , , ... , . Cuando sea un polinomio de grado cero en , tendremos que esos son todos los ceros de , es decir que todos los ceros de estarán en .
Supongamos que el grado de fuera mayor que 1. Pongamos . Aplicando la construcción anterior a , obtendremos una extensión de , donde habrá al menos un cero de . Como es un factor de y, por lo tanto, de , resulta que el nuevo cero es también un cero de . Si hemos hallado todos los ceros de , contendrá a dichos ceros. En caso contrario, repetimos el proceso anterior, hallando una extensión de conteniendo ceros adicionales de .
Repitiendo el proceso anterior, cuantas veces sea necesario, obtendremos una cadena de extensiones:
Como en cada extensión, obtenemos al menos un cero de y la cantidad de ceros es, a lo más, igual al grado de , tendremos que la cadena anterior acaba después de una cantidad finita de extensiones. Por lo que, hallaremos una extensión , para algún , donde el polinomio tendrá todos sus ceros. Este resultado lo enunciaremos como una proposición, luego de la siguiente definición.
Definición. (Cuerpo de Descomposición) Sea un cuerpo, irreducible. Llamamos cuerpo de descomposición de , a una extensión minimal de , tal que factoriza en factores lineales sobre (equivalentemente, tiene todos sus ceros en ).
Notemos que cualquier cuerpo que contenga todos los ceros de un polinomio es una extensión del cuerpo de descomposición del polinomio.
Formalizaremos la construcción anterior, en la demostración de la siguiente proposición.
Proposición 5. (Existencia de un Cuerpo de Descomposición) Sea un cuerpo, en un polinomio irreducible. Entonces, hay una extensión de que es un cuerpo de descomposición para .
- Demostración: Si el grado de es 1, entonces coincide con el cuerpo de descomposición. Supongamos que el polinomio tiene grado , , y que el resultado es cierto para todos los polinomios irreducibles de grado menor que .
Por una proposición anterior, hay una extensión de de , k[X]/\langle f\rangle,</math> donde tiene al menos un cero. Como muestran los ejemplos, es posible que esa extensión tenga más de un cero. Si los ceros de (habrá de ellos) están en , entonces será un cuerpo de descomposición para . En caso contrario, sean
, , los ceros de en . Por el teorema del factor tendremos que:
Donde será un polinomio con coeficientes en , pero de grado menor que . Si es irreducible, la hipótesis de inducción aplicada a nos producirá una extensión de que será un cuerpo de descomposición para y, por lo tanto, para . Si fuera reducible, procederemos por inducción con cada uno de sus factores irreducibles.
Elementos Trascendentales
[editar]Definición. (Elemento Transcendente) Sea un cuerpo y una extensión de . Cuando un elemento de no sea algebraico sobre (no sea cero de un polinomio con coeficientes en ), diremos que es transcendente sobre .
Ejemplo.
Consideremos a como extensión de . Se ha probado (Lindemann, 1882) que el número real es transcendente sobre . ¿Cuáles serán los elementos de ?
Otro importante número real transcendente sobre es (Hermite, 1873).Proposición 6. Sea un cuerpo y una extensión de que contiene un elemento transcendente sobre . Entonces, contiene una copia de y (el cuerpo de las fracciones racionales de ).
- Demostración: Consideremos la evaluación , . Sabemos que esa función es un homomorfismo de anillos. Además, es inyectiva, ya que no hay un polinomio no nulo tal que . Por lo que la imagen de es un subanillo de , por lo que contiene una copia de . Como, dicha copia es un dominio de integridad, tiene un cuerpo de fracciones (isomorfo a ) que estará contenido en , ya que los cuerpos son cerrados respecto a fracciones de sus elementos.
El Polinomio Minimal
[editar]Sea una extensión de . Sea un elemento de algebraico sobre . Sea el ideal de formado por todos los polinomios que tienen a como un cero. Como es un DIP, dicho ideal es generado por un polinomio mónico del menor grado posible entre los polinomios del ideal, al que daremos el siguiente nombre.
Definición. (Polinomio Minimal) Llamamos polinomio minimal de sobre , al polinomio mónico de menor grado que tiene a como uno de sus ceros.
Notemos que si es el polinomio minimal del elemento y es un polinomio tal que , entonces .
Sigue de nuestros trabajos anteriores la siguiente proposición para la adjunción de elementos algebraicos
Proposición 7. (Teorema de la Adjunción de Algebraico) Sea una extensión del cuerpo . Sea un elemento de que es algebraico sobre y sea su polinomio minimal de grado . Entonces, el subcuerpo de generado por y , consiste de todos los polinomios en de grado a lo más . Dicho cuerpo es isomorfo a .
Ejemplos.
Ejercicios
[editar]Automorfismos de Cuerpos
[editar]Recordemos que un automorfismo de un cuerpo es un isomorfismo de cuerpos de en si mismo. Los automorfismos de un cuerpo forman un grupo con respecto a la composición.
Proposición 8. Sea un cuerpo. Sea un subgrupo del grupo de automorfismos de . Sea el subconjunto de determinado por los elementos de que quedan fijos por los automorfismos en . Entonces, es un subcuerpo de .
- Demostración: Sea en , o sea un automorfismo cualquiera de . Entonces, . Luego, está en . Sean elementos de . Entonces, , como es cualquiera, concluimos que está en . Análogamente, para cualquier en , , y , lo que muestra respectivamente que es un subanillo, subanillo con identidad y subcuerpo de .
Nomenclatura. Diremos que es el subcuerpo fijo por los elementos del grupo de automorfismos es el subcuerpo fijo por .
Corolario 8.1. Sea un cuerpo. El cuerpo primo de es fijo para cada automorfismo de .
- Demostración: Sea cualquier automorfismo de . Como queda fijo por , cada elemento del subanillo generado por 1 queda fijo por , e igualmente las fracciones de los elementos de ese anillo. Por lo que el cuerpo primo queda fijo por todos los automorfismos de .
Proposición 9. Sea una extensión del cuerpo y sea un subcuerpo de . Sea el conjunto formado por todos los automorfismos de que dejan fijos cada elemento de . Entonces es un subgrupo del grupo de los automorfismos de .
-
Demostración: Claramente, no es vacío, ya que la identidad deja fijo cada elemento de y, por lo tanto, cada elemento de sus subcuerpos. Sean y elementos de . Entonces, para cada de se tiene que y . Sea en . Entonces, , lo que muestra que es cerrado respecto a tomar inversos. Igualmente, , lo que muestra que es cerrado por respecto a la composición. Por lo tanto, es un subgrupo del grupo de automorfismos de .
Notación. Sea una extensión del cuerpo . Denotaremos por al grupo de automorfismos de que dejan fijo a (los elementos de) .
Ejemplo.
Sea y . Sea . Entonces, para cada se tiene que
Es decir que cada automorfismo de queda determinado por la imagen por de . Digamos que , . Entonces, implica que , es decir que
Lo que implica que y . De donde, y . Por lo que tenemos solamente dos posibilidades para , la identidad o la conjugación .
Es decir que es un grupo cíclico de orden 2.La siguiente proposición resume las dos proposiciones anteriores para extensiones de cuerpo.
Proposición 10. (Teorema de Galois) Sea una extensión del cuerpo y sea . Entonces,
- Demostración: Ejercicio
La proposición establece correspondencia entre los cuerpos intermedios entre y y los subgrupos de . Dicha correspondencia puede usarse para estudiar la estructura de las extensiones en término de la estructura del grupo . La primera aparición de dicha correspondencia se debe al francés Evariste Galois (1811--1832). El problema era determinar cuando los ceros de un polinomio sobre podían expresarse usando las cuatro operaciones y radicales con los coeficientes del polinomio. Pensar, por ejemplo, en las fórmulas cuadrática o cúbicas. Galois determinó que una condición necesaria para lo anterior, era que el grupo de automorfismo del cuerpo de descomposición del polinomio, tuviera una cadena de subgrupos normales,
tal que cada fuera abeliano.
Observemos que si el cuerpo de descomposición de un polinomio tuviera como grupo de automorfismos a , dicha cadena no existiría y, por lo tanto, los ceros no podrían calcularse mediante fórmulas por radicales. Como hay polinomios de grado 5 que satisfacen lo anterior, se tiene la imposibilidad de la resolución de la ecuación general de quinto grado mediante radicales.
Ejercicios
[editar]Los Cuerpos Finitos
[editar]Los cuerpos finitos tienen característica positiva, es decir un número primo . Por lo que su cuerpo primo se identifica con . Sea un cuerpo finito, digamos con elementos. Entonces, el grupo multiplicativo, denotado por tiene elementos. Por el teorema de Lagrange, tenemos que para cada de se cumple que
| (21-01) |
Luego, para todo de , se cumple que
| (21--02) |
Nuestro primer resultado sobre cuerpos finitos, establecerá que su grupo multiplicativo es cíclico. Usando lo anterior, estableceremos la estructura de un cuerpo finito cualquiera.
El grupo multiplicativo de un cuerpo finito es cíclico
[editar]La demostración del resultado requiere de unos lemas previos. Es posible que dichos resultados hayan aparecidos anteriormente en el texto o los ejercicios, pero daremos aquí los enunciados y demostraciones para completitud. Otra demostración, usando un resultado anterior, aparece en un ejercicio al final de la sección.
Lema A. Sea un grupo y sean , elementos de con ordenes finitos y . Si y son relativamente primos, entonces se cumple lo siguiente.
- Demostración:
Lema B. Sea un grupo tal que para cada natural, la ecuación tiene a lo más soluciones. Entonces, el grupo es cíclico.
-
Demostración: Sea un elemento de tal que y sea . Por el teorema de Lagrange, para cada en se tiene que . Luego, contiene a todos los elementos de orden en . Como el orden de cada conjugado de un elemento en tiene orden , concluimos que es normal en . Luego, todos los subgrupos cíclicos de son normales en .
Sea un elemento de cuyo orden sea maximal entre los elementos de . Probaremos que .
Sea cualquier elemento de con orden igual a . Si entonces contiene un elemento de orden , lo que implica que está contenido en .
Supongamos entonces que . Entonces, hay un primo y un entero tales que , pero . Digamos que y con y . Como hay un elemento en tal que . Por la misma razón, contiene un elemento con . Como los ordenes de y son relativamente primos, y tienen solamente al elemento nulo en la intersección . Consideremos al elemento . Como
se tiene que está en . Como , tenemos que está en . Luego, , lo que implica que .
Por el Lema A, se tiene que tiene orden . Pero, ese número es mayor que el orden de , lo cual es una contradicción.
En conclusión, contiene a todos los elementos de , por lo que es cíclico.
Proposición 11. Sea un cuerpo finito. Entonces es un grupo cíclico.
- Demostración: Para cada natural, la ecuación tiene a lo más soluciones en un cuerpo. Luego, por el lema anterior, es cíclico.
Sea un entero mayor que 1 que no es un cuadrado. Entonces, para infinitos primos se cumple que la clase es un generador del grupo multiplicativo .
Estructura de un Cuerpo Finito
[editar]Sea un cuerpo finito, digamos con elementos. La característica de es un número primo . Sea un polinomio de grado , irreducible sobre . Sigue de la teoría general de los cuerpos que el cociente es un cuerpo que es una extensión de donde tiene al menos un cero, digamos . La teoría dice que está formado por todos los polinomios en de grado a lo más con coeficientes en . Como hay coeficientes y cada coeficiente se puede escoger de maneras diferentes, concluimos que tiene exactamente elementos. Hemos probado la siguiente proposición.
Proposición 12. Sea un cuerpo finito con , Si es un polinomio de grado , entonces la extensión tiene elementos.
Corolario 12.1. Sea un cuerpo finito y un elemento algebraico sobre . Entonces, el cuerpo que resulta al adjuntar , es finito,
-
Demostración: La adjunción es isomorfa como cuerpo a , donde es el polinomio minimal de sobre .
A continuación, veremos que cada cuerpo finito es de la forma anterior, con .
Sea un cuerpo con elementos de característica , primo, por lo que su cuerpo primo es .
Como el grupo multiplicativo es cíclico, tiene un generador que denotaremos por . Considerando la evaluación en de los polinomios con coeficientes en , obtenemos la función de en . Se sabe del capítulo los Anillos de Polinomios que dicha función es un homomorfismo de anillos. Como , tenemos que la función es suprayectiva. Sigue entonces, del teorema de homomorfismo de anillos que , donde es el núcleo de .el ideal es principal, está generado por un polinomio de grado positivo, el polinomio minimal sobre de . Como satisface la ecuación , tenemos que está en ese ideal, por lo que será un factor de . Por el teorema de homomorfismos de anillos, tenemos que . Hemos, por lo tanto, probado la siguiente proposición.
Proposición 13. Sea un cuerpo de característica , primo, que tiene elementos. Entonces, hay un número natural y un polinomio de grado , , irreducible sobre tales que , Además, , la clase de es un generador del grupo cíclico de y es un factor del polinomio .
Existencia de Cuerpos Finitos y Polinomios Irreducibles
[editar]La proposición 13 describe la estructura de un cuerpo con elementos, donde es un número primo. Pero, dado , ¿existe tal cuerpo? o equivalentemente, ¿hay un polinomio irreducible de grado ?
En esta sección, probaremos que tal cuerpo y polinomio efectivamente existen. Sea un número primo. Consideremos el polinomio sobre . Computando la derivada, obtenemos que que es igual a , ya que la característica del cuerpo base es . Pero, eso significa que no hay ceros comunes entre el polinomio y su derivada, por lo que el polinomio no tiene ceros múltiples (ver ejercicio al respecto).
Sea el cuerpo de descomposición de . Sabemos, por la proposición 5 que tal cuerpo existe y que es una extensión de que contiene a todos los ceros de . Por la generación del cuerpo de descomposición, se obtiene esencialmente "adjuntando" los ceros de , como cada adjunción produce un cuerpo finito y hay una cantidad finita de tales adjunciones, se tiene que es un cuerpo finito. Sea el subconjunto de formado por todos los ceros de . Probaremos que es un subcuerpo de . Para eso, necesitaremos un lema que discutiremos a continuación.
Recordemos que, en cualquier anillo conmutativo de característica , se cumple que , Tenemos, además la siguiente generalización.
Lema C. Sea un anillo conmutativo con identidad de característica , primo. Entonces, para todo natural se cumple que
-
Demostración: (Inducción.) El caso , es lo que recordamos arriba. Supongamos que la relación se cumple cuando . Entonces
Volvamos a la discusión del conjunto de los ceros de en el cuerpo de descomposición . Sean y dos de esos ceros. Entonces,
Todo lo anterior muestra que es un subanillo de , por lo que es un dominio de integridad. Como es finito, debe ser un cuerpo que es un subcuerpo de que contiene todos los ceros de . Pero. el cuerpo de descomposición es el cuerpo más pequeño que contiene todos lo ceros de . Luego . Además, como está formado por todos los ceros de , se tiene que . Hemos probado así el siguiente resultado.
Proposición 14. Sea un número primo. Para cada número natural hay un cuerpo extensión de tal que . está formado por todos los ceros del polinomio . Sigue de la proposición 13, el siguiente corolario.
Corolario 14.1. Sea un número primo. Para cada número natural . hay un polinomio irreducible de grado .
Sea un cuerpo con elementos. Sabemos que el grupo multiplicativo de es cíclico, lo que usamos en la demostración de la proposición 13, para que a partir de un generador del grupo cíclico, hallar un polinomio irreducible de grado . Dicho polinomio era el polinomio minimal del generador sobre . Ahora bien, hay generadores del grupo , por lo cual será posible hallar varios polinomios irreducibles de grado . Tomando dos polinomios irreducibles distintos, digamos y , se tiene dos cuerpos diferentes y que tienen cada uno elementos. Probaremos a continuación, que esos cuerpos son isomorfos, por lo que podremos decir que hay un único cuerpo con elementos.
Sean un cuerpo cualquiera con elementos y el cuerpo de descomposición de . Sea un generador del grupo multiplicativo de y sea el polinomio minimal de sobre . Por los resultados anteriores, tenemos que . Como también es un cero de (ver la ecuación 21-02, podemos considerar a como un elemento de . Sea , la evaluación en , que es un homomorfismo de anillos con núcleo . Por el teorema de homomorfismos que hay un isomorfismo de con su imagen en . Pero como dicha imagen tendría elementos, al igual que , concluimos que la imagen es todo . Es decir que es isomorfa con . Por lo que podemos afirmar lo siguiente.
Proposición 15. Dos cuerpos finitos con iguales cantidades de elementos, son isomorfos.
Convenio. La proposición anterior implica que para cada hay un único cuerpo con elementos (excepto por isomorfismos). Simbolizaremos tal cuerpo por . En particular, para primo, .
En algunos textos, se denota por al cuerpo . La notación corresponde a la expresión en inglés "Galois Fields" (cuerpos de Galois) que honra al matemático Evariste Galois.
Subcuerpos
[editar]Veremos, en esta sección, que tiene como subcuerpos exactamente a los , donde es un divisor de . Comenzaremos con un lema sobre divisibilidad de ciertos polinomios.
Lema D. En , , ssi, .
-
Demostración:
() Sea tal que .
Entonces, aplicando la fórmula para la sumatoria de series geométricas, tenemos que
Lo que prueba que .
() Sea con . Entonces,
Por la hipótesis y la parte anterior, tenemos que divide a y a . Por lo que divide a . Por razones de grado, lo anterior es imposible, a menos que . Es decir que .
Sea y sea un subcuerpo de . Entonces, para algún entero menor o igual a . Además, es un subgrupo del grupo cíclico , por lo que su orden debe ser un divisor del orden de , . Luego, por el lema anterior, .
Supongamos, ahora, que . Como el grupo multiplicativo de es cíclico y de orden , y como divide a dicho orden (por el lema), se concluye hay un subgrupo de orden del grupo multiplicativo . Esos elementos son todos los ceros no nulos del polinomio . Por lo que, junto con el 0, determinan el cuerpo de descomposición de ese polinomio, o sea, un cuerpo isomorfo a .
Hemos, así, probado la siguiente proposición.
Proposición 16. Los subcuerpos de son los cuerpos , donde es un divisor de .
Factorización de Xpn - X en Fp[X]
[editar]Como es un dominio de factorización única, el polinomio se puede expresar como un producto de irreducibles sobre . Sin perdida de generalidad, por ajuste de los coeficientes líderes, podemos suponer que todos esos polinomios son mónicos. Sea un factor mónico irreducible de de grado . Como tiene todos sus ceros en , tenemos que todos los ceros de están en . Sea uno de los ceros de , que será, por lo tanto, el polinomio minimal de sobre . Entonces,
Luego, por la proposición de subcuerpos, tendremos que .
Supongamos, ahora, que , entonces hay un polinomio mónico irreducible tal que el cuerpo es isomorfo a . Como , es un subcuerpo de . La isomorfía anterior, implica que tiene un cero en . Como , tenemos que ) (ver lema D), por lo que todos los ceros de están en . Por lo que todos los factores lineales de en son factores lineales de . Luego, .
Tenemos, por lo tanto la siguiente proposición.
Proposición 17. En , el polinomio es el producto de todos los polinomios mónicos irreducibles de grado , para todo que es un divisor de .
. Cantidad de irreducibles. Simbolizaremos por la cantidad de polinomios irreducibles mónicos en .
Corolario 17.1. Sea primo, para todo se cumple que
| (*) |
- Demostración: Calculando los grados en la factorización de .
Ejemplos. Sea un número primo.
Observación. Usando técnicas de la teoría de las funciones multiplicativas, específicamente la fórmula de inversión de Moebius, se obtiene la siguiente fórmula explícita
Donde es la función de Moebius, definida como
El lector interesado deberá buscar los detalles acerca de la fórmula de inversión en libros de teoría de números.
Ejercicios
[editar]
Comentarios
[editar]La Teoría de Galois. Recordemos la disputa central en los tiempos de Galois. Había desde varios siglos anteriores fórmulas para resolver las ecuaciones (polinómicas) de grados inferiores a 5. Dichas fórmulas obtenían las raíces de la ecuación (o sea los ceros del correspondiente polinomio) mediante expresiones que envolvían los coeficientes del polinomio, las cuatro operaciones y radicales.
Los trabajos de Ruffini y Abel mostraron que una fórmula general para ecuaciones de grado 5 (o mayores) era imposible. Lo anterior no impedía que algunas ecuaciones de tales grado tuvieran soluciones con los requisitos indicados. ¿Cuáles eran esas ecuaciones? La relación que Galois (Proposición 10) establece entre cuerpos intermedios de una extensión de un cuerpo base y los subgrupos del grupo de automorfismos, permitió caracterizar a dichas ecuaciones.
Los detalles de las relaciones entre las ecuaciones y los grupos se pueden hallar en Wikipedia:Teoría de Galois. Una magnifica exposición trazando la historia del tema, con referencias a fuentes originales, se halla en [2].
La teoría de Galois---o las ideas subyacentes--- ha tenido extensiones en el siglo XX, notablemente por Grothendieck[3] y Serre[4]. (Ver en Wikipedia en inglés la página "Grothendieck's Galois theory")
Notas
[editar]21. Los Tipos de Dominios
[editar]Introducción
[editar]El anillo de los Enteros es un dominio (de integridad) con algunas propiedades muy interesantes tales como la división euclídea, la factorización de manera única en primos y que sus ideales son todos principales.
Analizaremos dichas propiedades y sus relaciones. Para hacer lo anterior, estudiaremos tres categorías de dominios: dominios euclídeos (que tienen algo parecido al resultado de algoritmo de la división de Euclides), dominios de ideales principales (DIPs) y dominios de factorización única (DFUs).
Tal estudio estará fundamentado principalmente en las relaciones de divisibilidad y las propiedades de primos e irreducibles.
Veremos que, en general, se cumple que dominios euclídeos son DIPS y que los DIPs son DFUs, lo que se ilustra en la figura siguiente. En la última sección, mostraremos que las relaciones de inclusión entre esas clases son estrictas, es decir hay DIPs que no son euclídeos y DFU que no son DIPs.
Nuestros principales ejemplos serán los Enteros, los anillos de polinomios sobre un cuerpo y los subanillos de los Complejos de la forma
Resultará muy interesante ver que la aritmética en esos últimos dominios es dependiente del entero En algunos casos, por ejemplo tendremos que irreducibles siempre será primos, pero en otros no.
Hay una sección completa dedicada a los Enteros Gaussianos, . Además de proveernos con una serie de interesantes y bellos resultados, es una muestra del genio de Gauss.
En este capítulo, para indicar que y son asociados, escribiremos
Los Dominios de Factorización Única, DFUs
[editar]Recordemos que llamamos dominio de factorización única a un dominio donde cada elemento no nulo que no es una unidad puede escribirse como un producto de irreducibles, donde los irreducibles y las veces que aparecen son únicas, excepto por asociados. Decimos que ese producto es una descomposición del elemento en producto de irreducibles. Esto quiere decir que, es un DFU, ssi,
Nuestro ejemplo primero son los Enteros, donde el Teorema Fundamental de la Aritmética establece precisamente que se trata de un DFU.
Observación. Supongamos que el conjunto de elementos irreducibles de se haya particionado de acuerdo a las clases de equivalencia de la relación "es asociado con". En algunos casos, hay una manera natural de seleccionar un representante de cada clase. En tales casos, se puede utilizar dichos representantes para eliminar la referencia a asociados en el enunciado de la descomposición en producto de irreducibles.
| Irreducibles en un DFU son primos |
Sabemos que en un dominio cualquiera los elementos primos son irreducibles. Hemos visto ejemplos de dominios donde hay elementos irreducibles que no son primos, ver también en el ejemplo A de la sección de Contraejemplos. Sin embargo, cuando el dominio es DFU, se cumple que todos los irreducibles son primos como vimos en la proposición 2 del capítulo La Factorización de Polinomios.
El siguiente lema será usado más adelante.
Lema A. Sea un irreducible tal que divide a un elemento de un DFU Entonces, (o un asociado) aparece en cualquier descomposición en irreducibles de
-
Demostración La hipótesis implica que hay un elemento de tal que Descomponiendo por la unicidad de la descomposición, tenemos que (o un asociado) aparece en la descomposición de
Proposición 1. (Existencia de mcd y mcm) Sea un DFU. Dos elementos no nulos siempre tienen mcd y mcm.
- Demostración
(La demostración es el proceso usual para calcular el mcd y el mcm de dos números enteros cuando se conoce sus factorizaciones en números primos.) Sean y dos elementos no nulos de Sean la reunión de los irreducibles que aparecen en la descomposición de con los irreducibles que aparecen en la descomposición de Entonces, podemos poner que
donde los 's y 's pueden ser positivos o cero (cero cuando el irreducible no aparecía en la descomposición en irreducibles del elemento). Sea Entonces, es un mcd de y
Análogamente, pero usando el mayor exponente en cada descomposición, obtenemos el mcm; dejaremos al cuidado de lector la verificación de lo anterior.
En el ejemplo B de la sección de Contraejemplos, se muestra que es un dominio donde hay mcd de dos elementos, pero no mcm, por lo que ese dominio no puede ser un DFU,
Caracterización de los DFU
[editar]El objetivo de esta sección es obtener una caracterización de los DFU usando que irreducibles son primos y que se cumple la llamada condición de cadenas finitas de divisores propios que veremos a continuación
Cadenas Finitas de Divisores Propios
¿Cuántos divisores o factores propios tiene un elemento cualquiera? (Un divisor propio de un elemento es un divisor del elemento que no es una unidad o un asociado del elemento.)
Veamos la situación en un DFU. Sea un elemento que no es una unidad y sea un divisor propio de Entonces, hay un tal que Sean y las descomposiciones de y respectivamente. Entonces,
Sigue de la unicidad que cada uno de los debe aparecer en el lado izquierdo, es decir que hay un por lo que Es decir que cada factor propio está formado por un producto finito de los factores irreducibles de Por lo tanto, la cantidad total de factores de un elemento cualquiera es finita. Por lo que se cumple la siguiente proposición.
Proposición 2. En un DFU no hay una sucesión infinita de elementos tales que cada sea un factor propio de
Llamamos condición de cadenas finitas de divisores propios a la propiedad de la proposición.
El siguiente enunciado es una forma equivalente para la condición.
(CFD) En cualquier sucesión de elementos de tal que hay un tal que implica que
Usando esa noción, tenemos la siguiente proposición caracterizando a los DFUs. La demostración será una simple abstracción de una de las pruebas clásicas del Teorema Fundamental de la Aritmética.
Proposición 3. Sea un dominio cualquiera. Entonces, es un DFU, ssi,
-
Demostración La necesidad de las condiciones ha sido probada con anterioridad, por lo tanto, solamente tenemos que probar que son suficientes.
Primeramente, probaremos que para cada elemento no nulo y que no sea una unidad, tiene un factor irreducible, usando la condición de cadenas finitas. Si es irreducible, no tenemos nada que probar. Si no es irreducible, donde ni ni son unidades. Si alguno de ellos es irreducible, hemos hallado el factor irreducible. En caso contrario, donde ninguno de los factores es una unidad. Si uno de ellos es irreducible, hemos hallado el factor irreducible. Continuando de esta manera generamos una sucesión tal que cada elemento es un divisor propio del anterior, excepto por Por la condición de cadenas, el proceso se acaba, lo que muestra que el término donde la sucesión se estabiliza debe ser irreducible (ya que no tiene divisores propios).
Veamos la existencia de la descomposición en irreducibles. Sea un elemento no nulo que no es una unidad. Por lo probado anteriormente, tiene un factor irreducible digamos por lo que para un cierto elemento Si fuera una unidad, habríamos hallado nuestra descomposición. En caso contrario, no es una unidad, por lo que tiene un factor irreducible tal que Si fuera unidad, habríamos hallado la descomposición. En caso contrario, buscaríamos un factor irreducible de Este proceso acaba en un número finito de pasos, ya que la sucesión genera una cadena de divisores propios
la que no puede ser infinita por la hipótesis (ii).
(Unicidad) Aquí usaremos que irreducibles son primos. Supongamos que tenemos dos descomposiciones que producen el mismo elemento. Digamos que
| (*) |
donde los 's y los 's son irreducibles, y y son unidades.
Como irreducibles son primos, es un primo que divide al producto de la derecha y, por lo tanto, divide a uno de ellos, digamos a Como ambos, y son irreducibles, deben ser asociados. Por reenumeración de los podemos suponer que Por ser donde es una unidad. Cancelando el factor común en ambos lados de (*), obtenemos que
| (**) |
Repitiendo el proceso anterior cancelamos, con posiblemente después de otra reenumeración. Así, cancelaremos todos los irreducibles de la izquierda, ya que un irreducible no puede dividir a una unidad. Esto prueba que Pero, por la misma razón, no puede haber irreducibles a la derecha. Luego, y cada irreducible de un lado es asociado de uno en el otro lado.
Otra caracterización de los UFD
Veremos, a continuación, otra caracterización de los UFD usando la existencia de mcds en lugar de que los irreducibles sean primos.
Necesitaremos algunas propiedades de los MCD que revisaremos a continuación.
Sea un dominio tal que dos elementos no nulos siempre tienen MCD.
Lema B. Cualquier cantidad finita de elementos no nulos, tiene un MCD.
-
Demostración Sea un conjunto finito de elementos de Si por la hipótesis hay un mcd de los elementos de Supongamos el resultado válido para conjuntos con elementos. Consideremos ahora el caso en que Por hipótesis hay un y un Claramente, es un divisor común de todos los 's. Sea un divisor común de todos los . tenemos, entonces que divide a y, en consecuencia, a . Luego, es un mcd buscado.
Lema C. (Asociatividad del MCD)
-
Demostración Basta notar que ambos elementos son mcd de los elementos del conjunto
Lema D.
-
Demostración Sea y
Entonces, por lo que Luego para algún de Hay un tal que Luego, por lo que ; análogamente, Luego lo que implica que es una unidad. Es decir que
Lema E. Si y entonces,
-
Demostración Si el lema anterior, implica que Además, Luego,
La siguiente proposición muestra que la condición de que los irreducibles sean primos es equivalente a que haya mcd de elementos.
Proposición 4. Sea un dominio cualquiera donde dos elementos no nulos cualesquiera tienen un mcd. Entonces, cada irreducible es primo.
-
Demostración Sea un elemento irreducible de tal que Supongamos que y que Como es irreducible, lo anterior implica que y Por el lema E, lo que implica que Lo que contradice la hipótesis sobre . Luego, debe dividir a o a , o sea que es un elemento primo.
Tenemos, en forma inmediata, el siguiente resultado.
Corolario 4.1. (Segunda caracterización de los UFD) Un dominio es DFU, ssi,
| es UFD, cuando lo es. |
Este resultado fue probado en el teorema A del capítulo 20. Tiene importantes consecuencias como que y cuerpo, son DFUs. Por inducción, sigue entonces que y (polinomios en varias indeterminadas) son DFUs.
Ejercicios
[editar]Los Dominios de Ideales Principales
[editar]Recordemos que llamamos dominio de ideales principales, DIP a un dominio tal que cada ideal propio está generado por un elemento. Notemos que los cuerpos son trivialmente DIPS. También sabemos que y son DIPS (ver la proposición 19.2).
Proposición 5. Sea un DIP. Sea un elemento no nulo de Las siguientes propiedades son equivalentes:
-
Demostración La implicación (i) (ii) es general, ver la proposición 17.4.
((ii) (iii)) Supongamos que es un elemento irreducible de y sea tal que Si entonces o es un unidad. Si es un unidad, y son asociados, por lo que En caso contrario, es una unidad, por lo que Lo que prueba que el ideal es maximal.
((iii) (i))
Suponer que es un ideal maximal del dominio Entonces, es un cuerpo, por la proposición 17.6 Como cuerpos son dominios, el ideal es primo (proposición 17.7). Sigue, entonces, de la proposición 17.8 que es primo.
Sea un divisor propio de entonces lo que implica que está en Si estuviera en dividiría a por lo que y serían asociados. Luego, cuando es un divisor propio de es un subconjunto propio de
Sigue de la discusión anterior, que la condición de cadenas finitas de divisores propios es equivalente, en un DIP, a la siguiente condición:
Un dominio satisface la condición noetheriana [5], ssi, no hay una cadena infinita de ideales.
Equivalente, toda cadena de ideales ascendentes es finita.
Proposición 6. DIPS satisfacen la condición noetheriana.
-
Demostración Sea una cadena ascendente de ideales tales que
Sea la reunión de todos los es decir que
Veamos que es un ideal. Sean en Por definición de reunion, hay tales que está en un y está en Sea entonces como e son subconjuntos de tenemos que están ambos en Como es ideal, tenemos que está en y que está en para todo en Por lo tanto, esos elementos están en por lo que es un ideal. Como es DIP, hay un tal que Supongamos que esté en Entonces, pero como es la reunión de los Luego, Por lo tanto, para todo se tiene que por lo que
Como lo anterior implica que se cumple la condición de cadena finita de divisores y que los irreducibles son primos, concluimos que
Proposición 7. Los DIPs son DFUs.
La siguiente proposición es la generalización del teorema de Bezout para los Enteros--- dados dos enteros no nulos, podemos expresar el mcd de ellos como una combinación lineal de dicho enteros.
Proposición 10. (Teorema de Bezout) Sea un DIP y sean y elementos no nulos de Entonces, hay un elemento que es un mcd de y Además, hay elementos tales que
-
Demostración: Sean y elementos no nulos de un DIP Sea el ideal generado por dichos elementos, o sea Como todos los ideales de son principales hay un generador del ideal, o sea Por estar y en tenemos que es un divisor común de ambos. Por estar en hay elementos del anillo tales que
| (*) |
Si es cualquier divisor común de y la relación (*) implica que divide a Luego, es un máximo común divisor de y
Ejercicios
[editar]Los Dominios Euclídeos
[editar]Dijimos en la introducción que los dominios euclídeos representan la abstracción de la división euclídea en los Enteros. A continuación, tendremos la definición formal.
Definición. ({Dominio Euclídeo) Sea un dominio. Decimos que es un dominio euclídeo, ssi, hay una función (llamada el tamaño o la norma euclídea) tal que
Supongamos que es un dominio euclídeo con "tamaño" Como las unidades son divisores de cualquier elemento del dominio, tenemos que para todo unidad y no nulo, se cumple, por (i), que En particular, lo anterior es válido para ; pero como 1 es una unidad, para cualquier unidad Luego, para toda unidad Además, es el menor valor asumido por Es decir que el conjunto de los no nulo es un conjunto de números enteros acotado inferiormente por
Ejemplos de Dominios Euclídeos
[editar]Ejemplo.
El ejemplo prototipo es el dominio de los números enteros con En efecto, si hay un entero tal que ; de donde por lo que ya que Recordemos el teorema de la división euclídea que establece que para todo y enteros, podemos hallar únicos enteros y tales que con Claramente, de allí, sigue la segunda condición de la definición de dominio Euclídeo.
Ejemplo.
Sea el anillo de polinomios con coeficientes en un cuerpo Veremos que se trata de un dominio euclídeo con tamaño o estructura euclídea dada por el \text{gr}ado de los polinomios.
Cuando y son polinomios tales que ninguno de ellos es nulo y entonces
Para los polinomios, se tiene, también, un teorema de la división análogo al de la división euclídea de los Enteros. Es decir, dados polinomios y no nulo, hay polinomios y tales que donde o Es decir que el anillo de polinomios es un dominio euclídeo, con tamaño definido por el \text{gr}ado de un polinomio.
Probaremos, a continuación, que todos los dominios euclídeos comparten con los Enteros, la propiedad de que cada ideal es principal.
Proposición 11. Sea un dominio euclídeo con norma euclídea Entonces, es un DIP (cada ideal es principal). Cuando el ideal no es nulo, su generador, tiene el menor tamaño entre los elementos del ideal.
-
Demostración Sea un ideal no nulo.
Sea entonces es un subconjunto de los enteros acotado inferiormente, por lo que tiene elemento minimal. Sea cualquier elemento de tal que es igual al elemento minimal de Entonces, para cualquier en se tiene que con o Como, implica que concluimos que es un elemento de Luego, ya que Concluimos
que es un múltiplo de es decir que
Corolario 11.1. Los dominios euclídeos son DFUs.
Ejercicios
[editar]Los Enteros de Gauss
[editar]Recordemos que llamamos enteros de Gauss o enteros gaussianos a los elementos del dominio
En esta sección estudiaremos detalladamente el dominio de los enteros gaussianos. Además de su importancia como uno de los primeros dominios de números no tradicional, nos servirá para ilustrar diversas técnicas al trabajar con dominios euclídeos (ya que probaremos que lo es). Llamamos la atención, también, a observar las relaciones que hay entre la aritmética de este dominio y la teoría de los números enteros ordinarios.
Recordemos que llamamos norma del entero gaussiano al número entero denotado y definido como Se verifica que es multiplicativa, o sea que Cuando se cumple que (lo que gráficamente es el cuadrado de la distancia del punto al origen en el plano cartesiano). Notemos que si entonces
Empezaremos nuestro estudio con la siguiente proposición.
Proposición 12. Los enteros de Gauss son un dominio euclídeo con estructura euclídea dada por la norma. La demostración seguirá después de algunos lemas.
Lema F. Para todo complejo hay al menos un entero de Gauss tal que
-
Demostración (Gráficamente) Cualquier complejo se halla en un cuadrado cuyos vértices son enteros de Gauss. El punto más alejado de los vértices es el centro del cuadrado, cuya distancia a los vértices es Como la norma es el cuadrado de la distancia, se tiene el resultado.
(Algebraicamente.) Sea Sean el entero más cercano a y el entero más cercano a Luego, y Sea Entonces,
Lema G. Sean y enteros de Gauss, Entonces, hay enteros de Gauss y tales que
-
Demostración Usar el lema anterior para hallar un tal que Escribamos como
Sea Entonces,
Por lo que,
- Demostración de la proposición.
Solamente falta probar la condición (i) de la definición de dominio euclídeo. Sean y enteros de Gauss no nulos. Se tiene que Luego,
Lo que junto con el lema anterior, prueba lo afirmado.
Sigue de los trabajos generales anteriores que es un DIP y, en consecuencia, un DFU.
A continuación, nos preocuparemos de la divisibilidad en Como se trata de un DFU, elementos irreducibles son primos y viceversa. Mucho del trabajo relacionara primos en con primos en ; para distinguirlos hablaremos de primos gaussianos (en ) y de primos enteros (en ),
Unidades de Z[i]
[editar]Sea un entero gaussiano cuya norma es igual a 1. Entonces, se tiene que lo que implica que o Es decir está en Notemos que cada uno de esos enteros gaussianos es un unidad en (</math>i(-i)=1</math>).
Supongamos, ahora, que fuera una unidad de Entonces hay un tal que Luego, tomando norma y usando que es multiplicativa, tenemos que
Luego, Por lo que,
| 2 no es primo en . |
Observando que tenemos que el primo entero 2 no es irreducible en (ramifica) ya que ni ni son unidades. De hecho se trata de irreducibles.
Si tomando normas tenemos que de donde o o por lo que o es una unidad. Luego, es irreducible en Análogamente, se verifica que es irreducible, u observando que es un asociado de ya que
| Primos Enteros iguales a una suma de cuadrados. |
Sea un entero primo tal que con enteros. Como si se tiene que no es un primo gaussiano. Por ejemplo, etc.
| 3 es un primo gaussiano. |
Supongamos que Tomando normas tenemos que por lo que o Si se ve claramente que es imposible. Si entonces es una unidad. Si entonces y es una unidad. Luego, es un irreducible, por lo tanto, un primo gaussiano.
Primos de Z[i]
[editar]Para el estudio de los primos gaussianos, necesitaremos algunos resultados sobre los primos enteros que veremos a continuación.
En primer lugar, notemos que si es un primo entero impar entonces es de la forma o Veremos que la pertenencia a una de esas clases implica conductas diferentes en
El siguiente resultado será básico para nuestras consideraciones.
Lema H. (Estructura de )
Sea un primo entero impar.
-
Demostración Usaremos que sabemos que es un grupo cíclico de orden y propiedades de los grupos cíclicos. Ver las proposiciones 20.11 y 11.2.
Corolario H.1. Si entonces es un cuadrado en
-
Demostración Si es un elemento de orden 4 en entonces tiene orden 2, por lo que se debe tener que
Lema I. (Fermat) Un entero primo positivo puede representarse como la suma de los cuadrados de dos enteros, ssi, o
-
Demostración Supongamos que es impar.
Supongamos que y que
Entonces, por lo que es decir que tiene orden multiplicativo 4, lo que es imposible.
Supongamos ahora que Por el lema anterior, hay un tal que Es decir que
Considerando a como elemento de se tendría que
Si fuera un primo gaussiano o Como es entero, lo anterior significaría que dividiría la parte imaginaria de esos factores o sea a 1. Luego, no es un primo gaussiano. Luego, donde ni ni son unidades. Computando normas, tendríamos que
Luego, o uno de ellos tiene norma 1 y es, por lo tanto, una unidad, lo que no puede ser. Si
Los Primos Gaussianos
[editar]Lema J. Si es un entero gaussiano tal que es un entero primo, entonces es un primo gaussiano.
-
Demostración Sea Tomando normas tenemos que Como es un primo entero, o o ; es decir que o es una unidad,. En consecuencia, es irreducible, por o que se trata de un primo gaussiano.
<Lema K. Si es un primo gaussiano entonces o donde es un primo entero.
Si entonces o
Si entonces es de la forma y es un asociado de
- Demostración Supongamos que fuera un primo gaussiano. Consideremos la factorización en primos de Como en debe dividir a uno de los primos de dicha factorización. Luego, hay un en tal que
Computando las normas se tiene que
Por lo que (1) o (2) En el caso (1), es la suma de dos cuadrados, por lo que es 2 o un primo de la forma
En el caso (2), se tiene que por lo que es una unidad y y son asociados.
Se tiene que ya que 2 no es primo en Igualmente, si es de la forma por el teorema de Fermat, o sea que no es primo. Luego, debe ser de la forma
Proposición 13. (Los Primos de )
Los primos gaussianos o primos en son:
-
Demostración La parte b) sigue del lema anterior.
a) Si es primo de la forma que es compuesto en los trabajos anteriores muestran que debiera ser igual a la suma de dos cuadrados, por lo que no puede ser de la forma indicada.
Ejercicios
[editar]Contraejemplos
[editar]En esta sección, daremos algunos ejemplos que prueban la inclusión estricta de los dominios euclídeos en los dominios de ideales principales, y la de estos en los dominios de factorización única. Así, como otras excepciones.
Nuestro primer ejemplo, mostrara que hay dominios que no son DFU.
Ejemplo A.
Un dominio que no es DFU.
Sea Vimos en un ejemplo del capítulo La Divisibilidad es un irreducible de que no es primo, por lo que no puede ser un DFU. En consecuencia, tampoco puede ser o euclídeo.
Ejemplo B.
Un dominio donde dos elementos tienen mcd, pero no mcm.
Sea (ver el ejemplo anterior) y sea Entonces, 3 es un elemento irreducible que no divide a por lo que
Supongamos ahora que Entonces, excepto por un factor que fuera una unidad, tendríamos que Sin embargo, este valor para produce una contradicción, ya que (por el ejemplo anterior) 21 es un múltiplo común de 3 y pero no es un múltiplo de Sin embargo, es la única posibilidad lógica. En efecto, sea igual a Entonces, digamos que, Ya que es un múltiplo común, se debe tener que digamos que Tomando conjugados y multiplicando, tendremos que
Pero, por lo que Luego, y son enteros divisores de 21. Por lo que son iguales a 1, 3, 7, o 21.
Ejemplo C.
Un DFU que no es DIP:
Sea el anillo de los polinomios con coeficientes enteros. Vimos que es un DFU, ver corolario A.1 del capítulo La Factorización de Polinomios. Pero, mostraremos a continuación que no es un DIP.
Consideremos al ideal en y supongamos que fuera un DIP. Entonces, tendríamos un polinomio, digamos que generaría el ideal. Como 2 está en se debe cumplir que lo que implica que el grado de es cero y, por lo tanto, que es un elemento de Luego, debe ser una unidad, o sea 1 o o un asociado de o sea 2 o
Como (Si debe tener todos sus coeficientes pares, mientras que es mónico). Luego, como no puede ser un asociado de 2, por lo que debe ser igual a . Sin embargo, como está en debe haber polinomios tales que
Lo que es imposible, ya que no tiene términos constantes y todos los coeficientes de son pares.
Ejemplo D.
Se puede verificar, pero no es trivial, que es un DIP que no tiene estructura euclídea posible.
Ejercicios del Capítulo
[editar]Notas
[editar]Apéndices
[editar]A. Las Funciones
[editar]Introducción
[editar]En este apéndice, revisamos la noción de función y varias nociones asociadas. No todos los resultados son usados en el texto y están aquí para completitud de la exposición. Ver la sección de Comentarios para algunas observaciones sobre la terminología.
Las Definiciones
[editar]Definición. (Función) Llamamos función del conjunto en el conjunto a la asignación a cada elemento de de un único elemento de . La asignación puede ser una regla, una fórmula, una expresión verbal o cualquier cosa que nos permita dado un elemento de , identificar el correspondiente elemento de .
Notación y nomenclatura.
Ejemplos.
La clasificación de las funciones
[editar]Sea una función. Dado un elemento de consideramos la ecuación
Las soluciones de esa ecuación son todos los elementos de cuyas imágenes son iguales al elemento de . Dependiendo del conjunto solución para esas ecuaciones, tenemos la siguiente clasificación para las funciones.
Definición. (Suprayectividad, Inyectividad, Biyectividad) Sea .
Ejemplos.
La Composición de Funciones
[editar]Definición. (Composición de Funciones) Sean y . Llamamos composición de con a la función de en simbolizada por y definida por
Observación. Algunas veces tendremos la situación indicada en los diagramas siguientes:
Cuando, en tales diagramas, haya dos "caminos" de un conjunto a otro que representan iguales funciones (por composicion), decimos que el diagrama correspondiente es conmutativo. En el ejemplo anterior, tenemos un triángulo y un cuadrado conmutativo, lo que quiere decir que y respectivamente.
Proposición. La composición, cuando está definida, es asociativa.
- Demostración:
Proposición. Sea una función entonces:
-
Demostración: Trivial.
La siguiente proposición nos informa acerca de la relación entre la composición de funciones y la "yectividad" de las mismas.
Proposición. La composición de dos funciones inyectivas (resp. suprayectivas, biyectivas) es inyectiva (resp. suprayectiva, biyectiva).
- Demostración: Sean , y .
Caso Suprayectivo. Supongamos que y fueran suprayectivas. Debemos probar que para cualquier en , hay un en tal que . Como es suprayectiva debe haber al menos un en tal que . Por su parte, como es suprayectiva, se debe tener que hay un tal que . Luego,
Lo que prueba que la composición es suprayectiva.
Caso Inyectivo. Supongamos que y son inyectivas. Sean y elementos de que tienen la misma imagen por . Entonces,
Lo que implica que la composición es inyectiva.
Caso Biyectivo. Sigue de los casos anteriores.
La Función Inversa
[editar]Definición. (Inversa de una Función) Sea una función. Decimos que una función es una inversa de , si,
Proposición. Cuando tiene inversa, tiene exactamente una única inversa.
-
Demostración:
Sea y sean y inversas de . Entonces,
Nomenclatura. Cuando exista inversa, por la proposición anterior, dicha inversa será única. Por lo que podremos hablar de LA inversa de , a la que simbolizaremos por .
Proposición. Cuando la inversa de una función existe, es invertible, y su inversa es la función original.
-
Demostración: Directo de la definición, ya que
Proposición. La composición de dos funciones invertibles es una función invertible, cuya inversa es la composición de las inversas de las funciones originales, pero en orden inverso.
-
Demostración:
Sean y invertibles. Entonces,
Análogamente, se verifica que:
Por lo tanto, es una inversa de . Por la unicidad de tales inversas, tenemos el resultado.
Proposición. (Criterio para Invertibilidad) Una función es invertible, si, es biyectiva.
-
Demostración: Sea .
() Sea la inversa de. Sea en , como se tiene que , lo que prueba que es suprayectiva. Supongamos que . Tenemos que
Lo que prueba que es inyectiva. Como es suprayectiva e inyectiva es biyectiva.
() Supongamos que es biyectiva, entonces para cada en hay un único elemento tal que. Por lo tanto, la asignación tal que define una función tal que . Sea en , entonces es un elemento de tal que , por inyectividad, ; o sea que . Lo que prueba que es una inversa de .
Proposición. (Propiedades de Cancelación)
-
Demostración: Ejercicio.
Extensión al Conjunto Potencia
[editar]Sea un conjunto. Simbolizaremos por al conjunto potencia de , es decir al conjunto formado por todos los subconjuntos de .
Definición. (Imágenes Directas e Inversas) Sea una función.
Observación. Cuando es una función de en , algunas veces, se escribe en lugar de y en lugar de .
Nosotros usaremos nuestro convenio en el apéndice (pero no en el texto), excepto que la imagen directa de , que coincide con la imagen de se denotará usualmente por .
Proposición. (Propiedades de la Imagen Directa) Sea . Entonces, cuando , son subconjuntos de se cumple que:
-
Demostración: Ejercicio.
Proposición. Sean y . Entonces
-
Demostración:
Sea . Entonces, , ssi, hay
un en tal que , ssi, ,
ssi,
Proposición. (Propiedades de la Imagen Inversa Sea . Entonces, cuando , son subconjuntos de se cumple que:
- Demostración: Ejercicio.
Proposición. (Relaciones entre Imágenes Directas e Inversas) Sea . Entonces:
-
Demostración:
Proposición. Sean y . Entonces
-
Demostración:
Proposición. Sean y . Entonces
-
Demostración:
Descomposición Canónica de una Función
[editar]Proposición. Sea una función. La relación definida definida por es una relación de equivalencia.
-
Demostración: Ejercicio.
Teorema (Descomposición canónica de una función) Sea una función. Entonces, podemos factorizar como:
donde es la suprayección canónica que envía cada elemento en su clase de equivalencia; asigna el elemento en y es una biyección de en la imagen directa de por , ; y, es la inyección canónica definida por la inclusión.
-
Demostración:
Por la proposición anterior es una relación de
equivalencia; por lo que su conjunto cociente está definido.
Realmente lo único que necesitamos verificar es que está
bien definida y que es una biyección. Notemos que por definición de
, si está en entonces, ; lo que
muestra que está bien definida. Es claro además que
es suprayectiva. Si , se
tendrá que de donde , probando la
inyectividad faltante.
Comentarios
[editar]Terminología. La noción de función es básica en las matemáticas. Funciones aparecen en cualquier área de las matemáticas. No hay, sin embargo, un consenso universal acerca de como referirse a ellas.
Los siguientes nombres han sido usados para denotar funciones:
El uso de esos términos obedece a tradiciones (operadores, por ejemplo, para funciones entre espacios de funciones). Siguiendo el peso tradicional, nosotros usamos transformaciones para ciertas funciones en contextos geométricos.
La terminología de "aplicación" y "mapeo" responden más a consideraciones que llamaría folclóricas, es decir, son usadas en ciertos países y en otros no. Algunos autores e instructores usas esa terminología con fines didácticos, usan funciones para contextos numéricos y aplicaciones o mapeos para funciones entre conjuntos que no son numéricos. Es decir el nombre usado depende de la naturaleza de los objetos considerados. En Álgebra Abstracta, el énfasis es en las propiedades de las operaciones abstrayendo (es decir ignorando) la naturaleza de los elementos donde se trabaja. Principalmente, por esa razón hemos usado función en forma uniforme.
B. Las Relaciones
[editar]Introducción
[editar]Este apéndice contiene las definiciones de relaciones, relaciones de equivalencia, relaciones de orden, así como nociones asociadas.
Las Relaciones
[editar]Definición. (Relación) Llamamos relación entre elementos de un conjunto y elementos de un conjunto a cualquier subconjunto de . Cuando sea una relación, usualmente escribiremos en lugar de .
Cuando sea igual a hablaremos de una relación en el conjunto .
Definición. (Tipos de Relaciones) Decimos que una relación en un conjunto es:
Ejemplos.
Definición. (Grafo) Sea una relación en un conjunto . Llamamos grafo asociado a la relación al par de vértices y aristas, definido de la siguiente manera:
Los grafos se representan gráficamente de la siguiente manera:
Ejemplo.
La representación gráfica del grafo de la relación en el conjunto .

Las Relaciones de Equivalencia
[editar]Recordemos que llamamos relación de equivalencia a una relación reflexiva, simétrica y transitiva en un conjunto . Veremos la noción de partición del conjunto , que resultará ser equivalente a la noción de relación de equivalencia.
Definición. (Partición) Una partición de un conjunto es una colección de subconjuntos no vacíos de cuya reunión es todo y tal que dos a dos son disjuntos.
Proposición. Sea una partición del conjunto . Sea definida en , por , ssi, hay un tal que y pertenecen a . La relación es una relación de equivalencia en .
-
Demostración: La reflexividad y simetría son inmediatas. Veamos la
transitividad, si y , podremos hallar , tales que y están en , y y están en
. Resulta entonces que es un elemento común a ambos subconjuntos, pero como estos son disjuntos dos a dos, concluimos
que . Luego, y están en el mismo ; o sea, .
Definición. (Clase de Equivalencia) Sea una relación de equivalencia en un conjunto . Para todo en , llamaremos clase de equivalencia del elemento , al subconjunto de formado por todos los elementos de que son equivalentes con .
Notación o .
Cada elemento de una de las clases de equivalencia es un representante de dicha clase.
Proposición.
-
Demostración: Sea una relación de equivalencia en . Por la reflexividad, cada es un elemento de , lo que prueba que las clases de equivalencia no son vacías y que su reunión es todo . Supongamos que y tienen intersección no nula, digamos que . Entonces, implica que ; análogamente se tiene que .
Por simetría y transitividad, concluimos que . En
particular esto dice que y que . Sea un elemento cualquiera de ; por transitividad, nuevamente,concluimos que , o sea que . En otras palabras, es un subconjunto de . Pero, como los roles de y son simétricos en las relaciones anteriores, tendremos también que . O sea, . Es decir que las clases de equivalencia son subconjuntos no vacíos, cuya reunión es todo el conjunto y son disjuntas dos a dos. Luego, forman una partición de .
La segunda parte fue probada antes.
Definición. (Conjunto Cociente) Sea un conjunto y una relación de equivalencia en . Llamaremos conjunto cociente de por la relación al conjunto formado por todas las clases de equivalencias de . Notación: .
Las Relaciones de Orden
[editar]En esta sección, introduciremos la notación y la nomenclatura asociadas con relaciones de orden. Recordemos que una relación de orden parcial en un conjunto es una relación reflexiva, transitiva y antisimétrica.
Definición. (Conjunto parcialmente ordenado) Decimos que un conjunto es un conjunto parcialmente ordenado, cuando haya un orden parcial en .
Supongamos que es una relación de orden en un conjunto
. Llamaremos relación dual de a la relación definida por:
La relación dual de comúnmente se simboliza por . El grafo de la relación dual es el "mismo" que el grafo de la relación original, excepto que todas las flechas han invertido su sentido. La siguiente proposición es fácil de verificar.
Proposición. La relación dual de una relación de orden parcial es también una relación de orden parcial.
Los principales ejemplos de relaciones de orden parcial son la inclusión de conjuntos (entre subconjuntos de un conjunto fijo), "mayor que" o "menor que" en los conjuntos de números reales y la divisibilidad en los números enteros positivos. Notemos que la relación dual de "estar contenido" es "contiene a", y que "mayor que" y "menor que" son duales una de la otra.
Definición. (Elementos Comparables) Sea una relación de orden en . Decimos que dos elementos , de son comparables cuando se cumpla que o . En caso contrario, diremos que son incomparables.
Definición. (Orden Total) Decimos que un orden es total, cuando se cumpla que dos elementos cualesquiera del conjunto son siempre comparables.
Un conjunto totalmente ordenado es un conjunto provisto de un orden total.
Definición. (Elemento Maximal, Elemento Minimal) Decimos que un elemento de un conjunto parcialmente ordenado , con un orden parcial es maximal, si,
La siguiente proposición es de fácil verificación.
Proposición. Sea un conjunto parcialmente ordenado finito, con orden . Entonces hay al menos un elemento
maximal y uno minimal del conjunto.
Definición. (Orden Lineal) Un orden es lineal cuando es parcial y se satisface la siguiente relación de tricotomía: para todo , , una, y solo una, de las alternativas siguientes es válida:
Definición. (Cadena) Una cadena es un conjunto parcialmente ordenado cuyo orden además es lineal.
Definición. (Cotas) Sea un conjunto parcialmente ordenado. Decimos que un elemento de es una cota superior de un subconjunto de , si,
Dualmente, decimos que un elemento es una cota inferior de , si,
Definición. (Cota Superior Estricta, Cota Inferior Estricta) Sea un conjunto parcialmente ordenado.
Los siguientes principios, que aquí tomaremos como postulados, son
importantes en el trabajo con conjuntos infinitos.
Principio de Hausdorff. Cada conjunto parcialmente ordenado tiene una cadena maximal.
Lema de Zorn Cuando en un conjunto parcialmente ordenado, cada cadena tiene una cota superior, entonces el conjunto tiene elemento maximal.
Definición. (Reticulado) Llamaremos reticulado a un conjunto parcialmente ordenado tal que cualquier par de elementos , tiene cota superior e inferior estrictas.
Notación:
.
Definición. (Reticulado Completo) Un reticulado es completo, cuando cada conjunto no vacío tiene una cota superior y una cota inferior estricta.
Proposición. Si un conjunto parcialmente ordenado tiene un elemento que es cota superior de todo el conjunto
y si cada subconjunto de tiene cota inferior estricta,
entonces es un reticulado completo.
Ejemplo.
El orden anterior es un reticulado completo.
C. Los Sistemas Numéricos
[editar]Introducción
[editar]Los Sistemas Numéricos son los Naturales, los Enteros, los Racionales, los Reales y los Complejos.
Suponemos conocidas las maneras de efectuar computaciones con los elementos de esos conjuntos así como de sus principales propiedades algebraicas. Aquí solamente daremos un resumen de las mismas, algunas veces con una demostración, cuando no suponemos conocida la demostración.
Formalmente, uno tiene dos caminos para proceder con los Sistemas Numéricos.
Los Números Reales
[editar]El conjunto de números Reales se puede identificar con las expansiones decimales (finitas e infinitas). Formalmente, se supone que determinan un cuerpo ordenado completo.
La noción de cuerpo se estudia en el texto en los capítulos Los Anillos y Extensiones de Cuerpos. Un cuerpo es ordenado cuando hay una relación de orden total compatible con las operaciones. La noción de completo es más delicada, formalmente se pide axiomáticamente que "cualquier subconjunto no vacío tal que ha un número mayor que cada uno de sus elementos (cota superior), tiene una cota superior estricta, menor o igual que cualquier otra cota superior". Ese postulado implica entre otras cosas que cada expansión decimal representa a un número real, que los naturales no tienen cota superior (Propiedad Arquimediana) y que cada sucesión de Cauchy [1] converge. Aunque esas propiedades son muy importantes,para los efectos del texto consideraremos principalmente las nociones de cuerpo y orden. Nuestro desarrollo no será, por lo tanto, totalmente formal.
Los Naturales (), los Enteros () y los Racionales que veremos a continuación son subconjuntos de los Reales. Los Complejos que veremos más tarde, son una extensión de los Reales, o sea que los contienen.
Los Números Naturales
[editar]Decimos que un subconjunto de los Reales es un conjunto inductivo, ssi, (i) contiene al cero (0) y (ii) cuando está en , entonces también está en . Observemos que mismo es un conjunto inductivo.
Definición. (Naturales, ) Llamamos Naturales al subconjunto de que es la intersección de todos los conjuntos inductivos en . Un número natural es un elemento de .
Claramente, es un conjunto inductivo que está contenido en cualquier conjunto inductivo. Aplicando la definición tenemos que
Observemos, que siguiendo las tendencias recientes, incluimos al 0 en los naturales.
La definición nos dice que cuando sea un conjunto inductivo contenido en , deberá ser igual a (ya que está contenido en cualquier conjunto inductivo de ). Esta observación sirve de fundamento para la propiedad más característica de los Naturales: el principio de inducción matemática, usado frecuentemente en el texto.
Proposición. ( (Primer) Principio de Inducción (PIM)) Sea un enunciado que tiene sentido para cada número natural. Si se cumple que
Entonces, es válida para todo número natural.
-
Demostración: Sea el conjunto formado por todos los números naturales tales que el enunciado es válido. Sigue de las hipótesis de la proposición, que es un conjunto inductivo. Por lo que concluye que es igual a .
Se puede también probar lo siguiente. Proposición. (Segundo Principio de Inducción) Sea un enunciado que tiene sentido para cada número natural. Si se cumple que
Entonces, es válida para todo número natural.
Se verifica, por inducción, que los Naturales son cerrados respecto a la adición y a la multiplicación (de los Reales). Cuando <mamth>m</math> y son números naturales, se verifica que $M<n$, ssi, $m-n$ es un natural diferente de 0. De ahí, sigue que cualquier natural diferente de 0 es positivo.
Los Números Enteros
[editar]Definición. (Enteros, ) Decimos que un número real es entero, ssi, es natural positivo o o es un natural positivo.
Las Propiedades Básicas de los Enteros
[editar]Se verifica que los Enteros son cerrados respecto a la suma, resta y multiplicación. Además la multiplicación es cancelativa. En término de estructuras se trata de un dominio de integridad (ver definiciones en el capítulo Estructuras).
El Orden en los Enteros
[editar]Se verifica que , ssi, es un número natural positivo. Se verifica que Sigue de la definición de entero, que para cada entero se cumple una, y solo una, de las siguientes alternativas.
Como cada natural positivo es mayor o igual a 1, no hay un número entero entre y , ya que por ser no nulo y positivo sería natural positivo. Sigue, en forma inmediata de lo anterior, que cuando es un número entero no hay entero entre y .
Principio del Buen Orden (PBO)
[editar]Una de las propiedades más característica de los Enteros con relación al orden es el Principio del Buen Orden, que tiene bastante uso en el texto..
Proposición. (Principio del Buen Orden) Sea un subconjunto de . Si no es vacío, contiene un elemento minimal, es decir un número entero que es menor o igual que todos los otros elementos del conjunto.
-
Demostración: . Supongamos que no tuviera elemento minimal y sea el complemento en los Naturales de . Tenemos que no puede estar en , ya que sería un elemento minimal, por lo que está en . Supongamos que fuera un elemento de . Cualquier número natural menor que no puede estar en , ya que si hubiera tales números en $S$, el menor entre ellos sería un minimal de . Luego, todos los números en deben ser mayores o iguales a ; por lo que no puede estar en , ya que sería un minimal de . Por lo tanto está en . Por PIM, debe ser igual a , pero, esto implica que su complemento sería vacío, lo que contradice la suposición de que no fuera vacío.
Notemos que tal resultado no es válido para los Racionales. En efecto, si consideramos el conjunto de los Racionales formado por todos los recíprocos de enteros positivos, es fácil ver que ese conjunto no tiene un elemento minimal.
El Algoritmo de la División de los Enteros
[editar]El resultado de la siguiente proposición es conocido como el Algoritmo de la División (de Euclides).
Proposición. (Algoritmo de Euclides) Sea y números enteros tales que . Entonces, hay únicos enteros (cociente de la división de por ) y (residuo de la división de por ) tales que
-
Demostración: Suponer que . Considerar el conjunto . Haciendo se ve que contiene números positivos o cero. Por el PBO, hay un que es el menor de todos ellos. Mostraremos que . Si entonces, hallaríamos un tal que . Entonces, la relación implicaría que ; de donde, . Lo que muestra que sería un elemento de que es menor que el minimal , lo que no puede ser. Luego, . Lo que prueba la existencia de y como en la proposición.
Probaremos ahora la unicidad. Supongamos que con . De donde (***). Si , sigue inmediatamente que , por lo tanto la unicidad. Igualmente, si , entonces . Supongamos que . Sin perdida de generalidad podemos suponer que . Entonces, , o sea . Por (***) de be ser positivo, lo que implica que , por lo que . Vemos, entonces, que el lado derecho de (***) es mayor o igual que , mientras que su lado izquierdo es menor que . Como esto es imposible, obtenemos que .
Veamos ahora el caso donde . Aplicando el resultado obtenido a y , obtenemos que hay únicos y tales que
con . De donde
{{Eqn}|****}}
Si se tiene el resultado deseado. Si , sea , Sustituyendo en (****), obtenemos que
Lo que concluye la demostración.
Una consecuencia importante es la siguiente.
Proposición. (Identidad de Bezout) Sean y números enteros positivos y sea el máximo común divisor de y . Entonces, hay enteros , tales que
-
Demostración: Sea . Como contiene al (</math>x=1</math>, ) hay enteros positivos en . Por el PBO hay un menor entero positivo en , digamos que
| (*) |
Sigue directamente de (*) que cualquier divisor común de y divide a . Por el algoritmo de la división, hay , tales que
(**). Usando (*) obtenemos que
, de donde
Si fuera positivo sería un número positivo de que sería menor que el minimal positivo de , lo que no puede ser; luego, . Por (**) es un divisor de . Análogamente , se prueba que es un divisor de . En consecuencia, es un divisor común de y que es divisible por cualquier otro divisor común, luego es el máximo común divisor.
Los Números Primos
[editar]Recordemos que llamamos número primo a un entero positivo cuyos únicos factores positivos son él mismo o 1. Un número diferente de que no es primo se llama un número compuesto.
Propiedades de los Primos.
Teorema Fundamental de la Aritmética
Cada número entero , puede expresarse como un producto único de potencias de primos. La unicidad significa que los primos que aparecen en el producto, y sus exponentes, dependen solamente de .
- Demostración: [Esquema Abreviado de la Demostración] Usando el principio del Buen Orden se prueba que tiene al menos un factor primo. Si no es primo, con . Usando el segundo princpio de inducción, se concluye la existencia de un producto de primos iguales . La unicidad sigue de las propiedades de los primos.
Los Números Racionales e Irracionales
[editar]Los (números) Racionales () son los números reales que son iguales a una fracción de números enteros. La suma, resta, producto y cocientes de dos números racionales es un número racional
Un número racional es positivo si es igual a una fracción de enteros cuyo numerador y denominador son positivos.
Un número real es irracional, ssi, no es irracional.
Se verifica que cuando es primo no puede ser racional (suponiendo que lo es, se halla una contradicción al teorema fundamental.
Los Números Complejos
[editar]Llamamos número complejo a una expresión de la forma donde , son números reales e . Se define la suma y multiplicación por
Se verifica que tales operaciones tiene las propiedades usuales (en término de estructuras, determinan un cuerpo).
Comentarios
[editar]La construcción de los Reales a partir de los axiomas de Peano es más extensa que partiendo de los axiomas de cuerpo ordenado completo. Realmente es la prueba matemática de que tal objeto existe. Los lectores interesados pueden consultar [2] o a la monografía [3].
Notas
[editar]
D. Teoría de las Estructuras Algebraicas
[editar]Introducción
[editar]En el capítulo Las Estructuras Algebraicas se presentó la noción intuitiva de \textit{estructura algebraica} como consistente de un conjunto con una o varias operaciones. Varias veces, en le texto, se hizo referencias a una teoría más general de estructuras (ver las definiciones de subgrupo y de homomorfismo de grupos).
Presentaremos, en este apéndice, un tratamiento más cuidadoso de la noción de estructura, pero limitados a lo necesario para el texto.
La teoría de las estructuras tiene también otros nombres: por ejemplo, álgebra universal. La reciente teoría de categorías también contribuye al estudio de las estructuras. Finalmente, la teorías, más recientes, de programación de computadoras, con sus nociones de clases, superclases, descendientes, etc. tiene conexiones con las estructuras algebraicas. Una teoría general debiera incluir todos esos aspectos, pero excede los alcances de nuestro libro.
Las Operaciones
[editar]La noción básica es veremos es aquella de operación --aria
Definición. (Operación) Una operación --aria, en un conjunto es una función
Donde, cuando, , es el producto cartesiano de consigo mismo veces, o sea el conjunto formado por todas las --uplas ordenadas de elementos de . Por su parte, será el conjunto .
Una operación es una operación --aria para un cierto . El número se llama la aridad de la operación.
Ejemplos.
Definición. (Conjunto cerrado respecto a una Operación) Sea una operación --aria en . Un subconjunto es cerrado respecto a dicha operación, ssi, para todo se cumple que
Cuando un subconjunto de es cerrado respecto a una operación -=aria , tenemos asociada una operación en tal que para todo en se cumple que
Decimos que esa operación en es la restricción de (la operación global) a . Usualmente, denotamos la restricción por el mismo símbolo que la operación (global). Notemos que la operación y su restricción tienen igual aridad.
Notemos, también, que un subconjunto es cerrado respecto a una operación --aria , cuando .
Definición. (Función compatible con operaciones) Sea una operación en un conjunto y una operación de igual aridad en . Decimos que una función es compatible con la pareja , ssi, permuta con las operaciones, es decir que el siguiente diagrama de funciones es conmutativo.
Es decir que .
Notemos que si y son --arias entonces la conmutatividad del diagrama de compatibilidad es la siguiente
Es decir que .
Estructuras Algebraicas
[editar]Definición. (Estructura Algebraica) Una estructura algebraica es una pareja donde es un conjunto, llamado el conjunto portador o base de la estructura y es una lista donde los son operaciones. Nos referiremos a como la lista de parámetros de la estructura. Llamaremos tipo de la estructura a la lista de aridades correspondientes a las operaciones en la lista .
Cuando la lista sea clara del contexto, podremos referirnos a la estructura por el nombre del conjunto base.
Cuando en una estructura, suponemos propiedades especiales de las operaciones de la lista, llamamos axiomas de la estructura a dichas propiedades.
Ejemplos.
Cuando la estructura tiene un nombre podemos referirnos al tipo por el nombre de la estructura.
Definición. (Estructuras comparables y homólogas) Decimos que las estructuras y son comparables, ssi, hay una biyección de en tal que cuando a en le corresponde (por la biyección) en , entonces y tienen la misma aridad.
Decimos que las estructuras son homólogas, cuando sean comparables y las operaciones correspondientes satisfagan los mismo axiomas.
Luego, dos estructuras son comparables, cuando, después de una permutación de la lista de parámetros de una de ellas, tienen el mismo tipo. En el futuro, cuando digamos que dos o más estructuras tienen el mismo tipo, supondremos que las operaciones de una se han permutado de manera que ambas tienen el mismo tipo; es decir que operaciones situadas en la misma posición en la lista de parámetros tienen igual aridad.
Morfismos de Estructuras
[editar]Definición. (Morfismo) Sean y dos estructuras comparables de tipo . Llamamos morfismo (o --morfismo) de en a una función compatible con las parejas de operaciones correspondientes.
Se tiene claramente que la composición de morfismos es un morfismo. Cuando el morfismo sea inyectivo (resp, suprayectivo, biyectivo), podremos hablar de monomorfismo, (resp. supramorfismo, isomorfismo).
Denotamos por el conjunto de morfismos de tipo de en . Cuando , la composición provee a de una estructura de monoide, con neutro la identidad. es el grupo de los isomorfismos de la estructura.
Subestructura
[editar]Sea una estructura de tipo . Sea un subconjunto no vacío cerrado respecto a cada una de las operaciones en . Por lo que tenemos definida una estructura donde está formada por las restricciones de las operaciones en .
Definición. (Subestructura) Decimos que determina una subestructura de tipo de , ssi, la estructura restringida es homóloga a la estructura de . Notación:
Con las notaciones anteriores, la inclusión () de en es compatible con las operación restringida y la operación en .
Ejemplo.
Consideremos el monoide . (Enteros módulo 10). Sea . Veamos la multiplicación en
Vemos de la tabla que es cerrado respecto a la operación, además tiene un neutro . Por lo que es un monomio, que como estructura es comparable con la estructura de . Sin embargo, no es un submonoide, ya el conjunto base de una subestructura debe ser cerrado respecto a todas las operaciones, lo que en nuestro caso no se cumple, ya que no es cerrado respecto a la operación --aria que define al neutro 1 de .
Observación. Dada una familia de subconjuntos bases de subestructuras de una estructura que contienen a un subconjunto , se puede proveer a la intersección de todos los subconjuntos de la familia de una subestructura de . Tal subestructura será la \textit{estructura generada} por .
Observación. Cuando es una subestructura de , la función definida por la inclusión es un morfismo de las estructuras.
Superestructuras, Descendientes, Herencias
[editar]Definición. (Superestructura, descendiente) Sea y dos estructuras tales que o, y el conjunto de axiomas de está contenido en el conjunto de axiomas de . En tal situación decimos que es una subyacente o superesrtructura[1] de o que es un descendiente de . Denotamos dichas relaciones como o .
Cuando , cada propiedad (en particular, los axiomas) de son válidos para . Decimos que hereda las propiedades de . Las relaciones de super y descendencia son transitivas.
Ejemplos.
La estructura de magma es una super estructura de la estructura de semigrupo. Tenemos, las siguientes relaciones
Estructura Subyacente Cuando es una estructura, obtenemos estructuras subyacentes si nos olvidamos de una o varias operaciones, o de algunos axiomas. Esta es la terminología preferida de los algebristas.
Ejemplo.
Sea el monoide aditivo de los naturales. A partir de esa estructura podemos obtener tres estructuras subyacentes (o super estructuras):
Observación. Sea , , estructuras tales que y . Entonces, . Una subestructura de un descendiente de un tercera estructura, es también un descendiente de esa estructura. Por abuso de lenguaje, decimos que es una subestructura del tipo de de .
Comentarios
[editar]La exposición anterior pretendía mostrar que los asuntos de estructuras aunque simples no son triviales y que se debe ser cuidadosos con sus usos.
La noción de estructura puede expandirse a considerar lista de parámetros no homogéneas. Es decir que además de operaciones, incluyan relaciones (por ejemplo, para un cuerpo ordenado), predicados e inclusive otras estructuras.
Ejemplo.
La Estructura de Anillo puede considerarse como una descendiente de la estructura de grupo abeliano, por lo que podría representarse como
Pero, también podríamos escribir
para destacar que se trata de un grupo abeliano (que aparecerá invariablemente) pero que la multiplicación puede tener diferentes propiedades, dando origen a descendientes tales como dominios, anillos con división, cuerpos, etc. También podríamos poner
Dejaremos el tema aquí, porque creemos haber cumplido con lo anunciado en la introducción.
A quien pudiera interesarle el tema, le recomendamos que inicie una búsqueda en la WEB de los temas "Álgebra Universal", "Estructuras Algebraicas" (a veces, aparece como sinónimo de "Álgebra Abstracta").
Notas
[editar]E. Los Grupos Geométricos
[editar]Introducción
[editar]En este apéndice, veremos algunos grupos que tienen su origen en la geometría plana (usando vectores). Nuestro interés primordial será en los aspectos algebraicos por lo que referiremos los aspectos geométricos a textos de Geometría.
Queremos describir algebraicamente las congruencias del plano. Congruencias son transformaciones del plano que preservan la distancia entre puntos (la distancia entre las imágenes de dos puntos es igual a la distancia entre los puntos originales.)
Hay dos tipos importantes de congruencias:
Sigue del teorema de Cartan--Dieudonné (ver capítulo Acción de Grupos ) que todas las congruencias (en particular, las rotaciones) son producto de a lo más tres reflexiones. En la terminología de grupos, las reflexiones generan al grupo de las congruencias.
Necesitaremos para nuestra exposición una breve introducción al Álgebra Lineal del plano y a su geometría basada en vectores.
El Plano Vectorial
[editar]El plano cartesiano consiste de los pares ordenados de números reales a los que llamaremos puntos. Cuando sea un punto, supondremos que sus componentes son , a menos que diga algo distinto. Consideraremos, además, a como un plano vectorial, lo que quiere decir que consideremos a sus elementos como vectores. Intuitivamente, pesaremos a como una flecha que empieza en el origen y acaba en el punto . La punta de la flecha, que identificamos con , nos da tanto una posición---el punto como un "largo" y una "dirección".
Algebraicamente, consideraremos all plano vectorial provisto de una suma por componentes:.
Además, consideraremos una multiplicación por escalares (en el contexto vectorial, llamamos escalares a los números reales y los simbolizamos por letras griegas.).
Se verifica que esta multiplicación es compatible con la suma.
Proposición 1. (Propiedades de la Multiplicación por Escalares) Sean y escalares, y vectores (puntos del plano).
-
Demostración: Ejercicio.
Subgrupos de R2
[editar]Notemos que la suma por componentes define una estructura de grupo en . Cuando sea un vector no nulo, denotaremos por al conjunto formado por todos los múltiplos escalares de , es decir, . Supongamos que y son elementos de , entonces
Lo que prueba que es cerrado respecto a la suma y a tomar opuestos aditivos. Como el vector nulo es también un múltiplo escalar de , tenemos, en la terminología de grupos, que un subgrupo del grupo . (Además, como , es cerrado respecto a la multiplicación por escalar, lo que en la terminología del Álgebra Lineal dice que es un subespacio vectorial de ).
Sean y vectores no nulos, entonces cuando , se cumple que . Lo que implica que los múltiplos escalares de coinciden con los múltiplos escalares de , o sea que
-
Cuando y son vectores no nulos, se cumple que
, ssi, uno de ellos es múltiplo escalar del otro.
Proposición 2.Sean y vectores no nulos. Entonces, , ssi, .
-
Demostración: () Supongamos que , entonces
y , por lo que
() Suponer que . Entonces, (*). Si , entonces implica que ya que . Luego,
Por un argumento similar, si , obtenemos que es un múltiplo escalar de . Supongamos ahora que y no son nulos. Dividiendo por en ambos lados de la ecuación (*) obtenernos
| (**) |
Llamando al valor común de las fracciones en (**), se tiene que
.
Si denotamos por la matriz cuyas columnas son los componentes de los vectores y , la condición de la proposición anterior es equivalente a afirmar que el determinante de dicha matriz es nulo.
Notemos que si y son vectores no nulos tales que entonces se tiene que
En efecto, si hubiera y no nulos, se tendría que es un múltiplo escalar de .
Definición. (Vectores Paralelos) Decimos que dos vectores no nulos y son paralelos o linealmente dependientes, cuando uno de ellos sea múltiplo escalar del otro. En caso contrario, decimos que los vectores son linealmente independientes.
Ejemplo.
Los vectores y son linealmente independientes.
Proposición 3. Sean , vectores linealmente independientes del plano. Entonces, para todo podemos hallar escalares únicos , tales que
| (*) |
-
Demostración: Escribiendo la ecuación (*) en términos de componentes, tenemos que
Se sabe (del álgebra elemental) que tal sistema de ecuaciones tiene soluciones únicas, ssi, el determinante del sistema no es nulo, pero esta es precisamente equivalente a la condición de que y sean linealmente independientes.
Definición. (Base y Coordenadas) Sean un conjunto formado por dos vectores. Decimos que es una base del plano, ssi, podemos expresar cada como una combinación lineal de y , es decir que hay escalares y tales que
Además, los escalares y son únicos, y se llaman las coordenadas de respecto la base .
Las coordenadas de se presentarán usualmente como una matriz columna. En la notación de la definición, se pone
El par , determina una base llamada base canónica del plano. Las coordenadas de son precisamente y .
Revisión de la Geometría Plana
[editar]Llamamos figura a cualquier subconjunto del plano.
Líneas. Llamamos línea a una figura tal que sus puntos son todos de la forma
donde y son vectores.
Es decir que
Sea , un vector no nulo [2]. Cuando es un punto de una línea decimos que la línea pasa por el punto. Como , tenemos que la línea pasa por . Llamaremos a un vector director de la línea y a la dirección de la línea.
Observaciones Sea .
Decimos que dos líneas son paralelas cuando tienen igual dirección. Luego, dos líneas son paralelas cuando tienen vectores directores que son paralelos.
Sigue de lo anterior, que dada línea y un punto , hay una única línea que pasa por y es paralela a ,
Se prueba que cuando dos líneas no son paralelas entonces tienen un único punto en común. Por su parte dos líneas paralelas, o son iguales o son disjuntas.
Ecuación Cartesiana de una Línea Sea . Entonces, cuando , tenemos, poniendo , que
Escribiendo las coordenadas aparte, tenemos que
Eliminamos (el parámetro) multiplicando (i) por y (ii) por , y restando posteriormente,para obtener
La última ecuación se dice que es una ecuación cartesiana de la línea.
Esta ecuación aparece en los tratamientos elementales de la geometría (algebraica) del plano
Supongamos que tenemos la ecuación (*) donde . Mostraremos que dicha ecuación es la ecuación cartesiana de una línea.
(Caso ) La ecuación (*) es equivalente a
Si ponemos
vemos que es un punto de la linea . Además, es fácil ver que la ecuación (*) es una ecuación cartesiana de dicha linea.
(Caso ) La ecuación (*) se reduce a que corresponde a la línea
Proposición 4. Cada línea tiene una ecuación cartesiana de la forma
Viceversa, todos los puntos satisfaciendo una ecuación de esa forma, determinan una línea.
Corolario 4.1. La línea con ecuación cartesiana tiene como dirección a la línea con ecuación cartesiana .
Las Transformaciones del Plano
[editar]Una transformación del plano es una función del plano en si mismo. En contexto geométrico, no necesariamente las transformaciones son biyectivas, por ejemplo la proyección del plano en el eje , . Sin embargo, para nuestros propósitos, las transformaciones interesantes serán biyectivas. Las transformaciones biyectivas determinan un grupo, el grupo simétrico del plano que denotaremos por . Llamamos grupo de transformaciones a cualquier subgrupo de . Notemos que un conjunto no vacío de transformaciones biyectivas determina un grupo de transformaciones cuando es cerrado respecto a la composición de funciones y a tomar inversos.
Las Traslaciones
[editar]Definición. (Traslación) Dado un vector , llamamos traslación por y denotamos por a la transformación tal que
Observaciones (Propiedades de las Traslaciones)
Sigue de lo anterior que el conjunto de las traslaciones determina un grupo de traslaciones denotado por . Notemos que la primera de las relaciones anteriores implica que la función de en es un homomorfismo de grupos que es claramente suprayectivo. Como implica que , la función anterior es un isomorfismo de grupos. Es decir, que como grupos, el grupo de las traslaciones y el grupo son isomorfos.
Proposición 5.Las traslaciones envían líneas sobre líneas paralelas a la original.
-
Demostración: Sea la traslación por y sea . Entonces, para todo en , tenemos que
Lo que prueba que es un punto de la linea Sea , entonces
lo que implica que . Las líneas y son paralelas porque tienen la misma dirección.
Corolario 5.1. Traslaciones preservan paralelismos entre líneas.
Las Transformaciones Lineales
[editar]Las transformaciones lineales provienen de la estructura de espacio vectorial del plano, es decir son transformaciones compatibles con la suma de vectores y con la multiplicación por escalar.
Definición. (Transformación Lineal) Llamamos transformación lineal del plano a una función tal que
Ejemplo.
Sea . Definimos una transformación de en si mismo por
(Observemos que escribimos el punto como una matriz columna, o sea como sus coordenadas respecto a la base canónica)
Se verifica por computación directa o aplicando propiedades de la multiplicación de matrices que
o sea que es lineal.
Decimos que es la transformación lineal definida por la matriz y la denotaremos simplemente por .
Veremos a continuación, que una vez seleccionada una base del plano, cada transformación lineal es equivalente a la transformación lineal definida por una matriz (usando las coordenadas respecto a la base seleccionada).
Sea una base del plano y sea una transformación lineal. Supongamos que las coordenadas de y son respectivamente y . Sea las coordenadas de respecto a la base . Es decir que
Luego,
Es decir, que en término de coordenadas.
Por lo que el efecto de es equivalente a multiplicar por una matriz que tiene en la primera (resp. segunda) columna las coordenadas de (resp. de ).
Las transformaciones lineales biyectivas corresponden a las matrices invertibles o sea aquellas que tienen determinante no nulo.
Grupo Lineal. Llamamos grupo lineal de dimensión 2 al grupo que denotamos por y que está formado por todas las matrices invertibles (con entradas reales).
Interpretaremos cada matriz como una transformación lineal biyectiva respecto a la base canónica.
Observación. Se puede definir un grupo lineal interpretando las matrices con respecto a una base diferentes de la canónica. Un resultado de Álgebra Lineal, establece que es conjugado con en el grupo , y que, por lo tanto, se trata de grupos isomorfos.
Acción de las transformaciones lineales biyectivas
[editar]Sea en y sea . Entonces, si es un punto de se tiene que
| (*) |
Como es biyectiva, , luego es un punto de la línea . Sea un punto de la línea , entonces , lo que prueba que .
Proposición 6. Las transformaciones lineales biyectivas envían líneas sobre líneas. Además, preservan el paralelismo entre líneas.
Relaciones de las traslaciones con las transformaciones lineales
[editar]Lema A. Sea una transformación lineal (cualquiera) y la traslación por , entonces .
-
Demostración:
El Grupo Afín
[editar]Definición. (Grupo Afín) Llamamos Grupo Afín al grupo de transformaciones generado por el grupo de las traslaciones y el grupo lineal. Simbolizamos dicho grupo por y decimos que sus elementos son las transformaciones afines del plano.
Sea una transformación afín. Sigue de la definición que es un producto de la forma
donde los son traslaciones y los son transformaciones lineales biyectivas. Sigue del lema A que podemos agrupar primero las traslaciones y luego las transformaciones lineales de modo que , donde es una traslación y es lineal. Tal representación es además única. En efecto si
En la última igualdad, tenemos en el lado izquierdo a una traslación y una transformación lineal a la derecha. Como transformaciones lineales siempre fijan al vector nulo, la traslación de la izquierda debe fijar al vector nulo. Como la única traslación que fija puntos del plano es la identidad, se tiene que , de donde . De ahí, sigue que también se cumple que .
Decimos cuando , que es la traslación de y es la parte lineal de .
Notemos que sigue de nuestro trabajo con traslaciones y transformaciones lineales biyectivas, que las transformaciones afines envían líneas sobre líneas y que preservan el paralelismo entre líneas.
- Se verifica en cursos de Geometría que las transformaciones afines pueden caracterizarse como las transformaciones biyectivas del plano que envían líneas en líneas. Dicho resultado se cita a veces como el "teorema fundamental de la geometría afín".
Proposición 7.El grupo de las traslaciones es un subgrupo normal del grupo afín. El grupo cociente es isomorfo al grupo lineal .
-
Demostración: Sea la función que asigna a cada transformación afín su parte lineal . Veamos que se trata de un homomorfismo de grupos
Como, cada es iguala , , se trata de un supramorfismo, cuyo núcleo son las traslaciones. Luego, es normal en . Por el teorema de Noether (ver capítulo Teoremas de Homomorfismos), se tiene que
La Geometría Euclídea
[editar]Las congruencias son las transformaciones que preservan la distancia entre puntos del plano. Para definirlas propiamente, necesitamos una noción de distancia. En los curso básicos, usando el teorema de Pitágoras, se define la distancia entre los puntos y como
Podríamos usar esa definición como definición de distancia, pero usaremos un camino distinto, más propio de la geometría vectorial. Definiremos algo llamado producto interior de vectores, que nos servirá para definir las nociones de largo y distancia.
El Producto Interior
[editar]Definición. (Producto Interior) Llamamos producto interior [3] a la función que asigna a cada par de vectores de el número real denotado por y definido como
Proposición 8. (Propiedades del Producto Interior)
-
Demostración: Computaciones directas.
La primera propiedad dice que el producto interior es lineal en su primer argumento, por la simetría de la segunda propiedad, tenemos que también es lineal en el segundo argumento. Por lo que se recuerda las propiedades anteriores, diciendo que el producto interior es bilineal (lineal en cada argumento), simétrico (PI-2) y positivamente definido (PI-3).
Ortogonalidad y Perpendicularidad. Decimos que dos vectores son ortogonales cuando su producto interior es nulo. Notación .
Sigue de las propiedades del producto interior que si , cualquier múltiplo de es perpendicular a .
Decimos que dos líneas son perpendiculares u ortogonales cuando tienen vectores directores ortogonales. Sigue de la observación anterior que cualquier par de vectores directores sirve para establecer la perpendicularidad de dos líneas.
Proposición 9. Sea un vector no nulo. Los vectores perpendiculares a determinan una línea que pasa por el origen, que denotaremos por y que tiene como un vector director a .
-
Demostración: Sea perpendicular a . Entonces, , ssi,
| (*) |
que es la ecuación cartesiana de una línea, ver la proposición 4.
Resolvamos la ecuación (*) para y . Es decir hallemos vectores perpendiculares a . Si , (*) implica que , lo que implica que . Luego,
Lo que prueba que, en este caso es un vector director de . Supongamos que , entonces (*) implica que ; de donde
Lo que termina la prueba.
Sea la línea con ecuación cartesiana
| (*) |
Sea un punto cualquiera de la línea. Entonces,
. Sustituyendo en la ecuación (*), tenemos que:
La siguiente proposición sigue de esos cálculos.
Proposición 10. La ecuación representa una línea que pasa por un punto y tal que sus vectores directores son perpendiculares al vector que se dice que es un vector normal a la línea.
Largos y Distancias
[editar]Largo. Llamamos largo del vector al número real simbolizado por y definido como
| . | (Largo) |
Distancia. Usando la definición de largo, tenemos que
Es decir que podemos definir la distancia entre y como
| (Distancia) |
Ejemplo.
Sea y la base canónica del plano. Dichos vectores tienen largo 1 y son ortogonales entre si. Por lo que la base se llama ortonormal. Notemos, además .
Propiedades
[editar]Proposición 11. (Cuadrado del Binomio para PI) Sean , dos vectores.
| (Ec-Bin) |
donde .
-
Demostración:
Corolario 11.1. (Teorema de Pitágoras) Si y son ortogonales.
Despejando el producto interior en la fórmula (Ec-Bin), obtenemos
| (PI-Form) |
Sea donde y es la base canónica del plano. Entonces,
Análogamente, obtenemos que .
Transformaciones Ortogonales
[editar]Definición. (Transformaciones Ortogonales) Una transformación lineal es ortogonal, ssi, preserva el producto interior. Es decir, ssi, para todo , se cumple que
Proposición 12. Las transformaciones ortogonales preservan largos y distancias entre puntos.
-
Demostración: Sean , puntos y sea ortogonal.
Sea una transformación lineal que es una congruencia. Entonces, para todo se tiene que
Es decir que las congruencias lineales preservan largo de vectores. Proposición 13. Las congruencias lineales son transformaciones ortogonales.
-
Demostración: Sea una congruencia lineal. Aplicando la fórmula (PI-Form) tenemos que
Simetral Ortogonal
[editar]Sean y dos puntos del plano. Buscaremos una ecuación para la figura determinada por todos los puntos que equidistan de y .
Punto Medio. Sea se tiene que
Lo que dice que . Además, ; lo que prueba que está en la línea que pasa por y . es el punto medio entre y .
Sea un punto cualquiera que equidista de y . Se tiene que
Sigue de la proposición 9, la siguiente proposición.
Proposición 14. Los puntos que equidistan de dos puntos es una línea que pasa por el punto medio de los dos puntos y es perpendicular a la línea que pasa por los puntos. Llamamos simetral ortogonal de los puntos y a la línea de la proposición.
El Grupo Euclídeo
[editar]Definición. (Congruencias) Llamamos congruencia a una transformación afín que preserva la distancia entre puntos.
Denotamos por al conjunto de todas las congruencias.
Ejemplo.
Las traslaciones son congruencias.
Sea , entonces,
Proposición 15. es un subgrupo del grupo afín del plano llamado el grupo Euclídeo del plano. La parte lineal de una congruencia es una transformación ortogonal. Las transformaciones ortogonales determinan un subgrupo, , llamado el grupo ortogonal. El grupo de las traslaciones es también un subgrupo del grupo euclídeo.
-
Demostración: La identidad es una congruencia. Sean y congruencias.
Lo que muestra que las congruencias determinan un subgrupo del grupo afín.
Sea una congruencia afín. Entonces, es una congruencia, por ser composición de congruencias, y es lineal, por lo tanto, es una transformación ortogonal.
El Grupo Ortogonal
[editar]¿Cómo son las matrices de una transformación ortogonal? Sea una transformación ortogonal y consideremos la base ortonormal canónica . Sean y . Como transformaciones ortogonales preservan largos y productos interiores, tenemos que
(Luego es otra base ortonormal del plano.) La matriz determinada por tiene como columnas a las coordenadas de , respecto a la base canónica. Supongamos que . Como se debe cumplir que . Como es perpendicular a se tiene (por proposición 9) que . Como , tenemos que . Es decir que tenemos dos posibilidades para ; por lo que las matrices tienen una de las formas siguientes:
donde . Notemos que en el primer caso el determinante de la matriz es 1, mientras que en el segundo es .
Es fácil verificar que ambos tipos producen trasformaciones ortogonales.
La función determinante (restringida a ) tiene imagen y su núcleo es el subgrupo normal, denotado por , formado por todas las transformaciones ortogonales con determinante 1.
Buscaremos puntos fijos para ambos tipos de transformaciones ortogonales. Recordemos que las transformaciones lineales fijan el origen.
(Caso I) Sea con . Sea , entonces , ssi,
Escribiendo la ecuación matricial como sistema de ecuaciones, obtenemos que
Lo que es equivalente a
El último sistema tiene soluciones no triviales (diferentes de ), ssi, su determinante es cero. El determinante del sistema es
Por lo tanto, el determinante es nulo, ssi, , lo que implica que ; o sea, cuando es la identidad.
Por lo que, cuando una matriz tiene la forma (I) y no es la identidad, el único punto fijo será el origen. Por lo que cada punto se mueve a un punto que está a igual distancia del origen que la distancia de al origen. Informalmente podemos decir que se mueve sobre la circunferencia de centro el origen y radio . Lo que nos dice que se trata de una rotación alrededor del origen.
Se acostumbra definir el ángulo de la rotación como el ángulo tal que
Llamando a la rotación por vemos que
Usando las definiciones anteriores de coseno y seno, junto con las propiedades de las transformaciones ortogonales, se pueden deducir las relaciones trigonométricas básicas tales como
(Caso II) Sea con . Sea , entonces , ssi,
Escribiendo la ecuación matricial como sistema de ecuaciones, obtenemos que
Lo que es equivalente a
El último sistema tiene soluciones no triviales (diferentes de ), ssi, su determinante es cero. El determinante del sistema es
Por lo tanto, siempre hay soluciones no triviales del sistema. Un punto está fijo por , ssi, {{Eqn|*}}
Si entonces que es una transformación que intercambia el eje con el eje , dejando la diagonal principal () fija punto a punto.
En forma más general, si se tiene por la ecuación (*) que está fijo por . Si queda fijo, entonces , es decir que deja fijo punto a punto a la línea .
Por la forma de la matriz, nunca puede ser la identidad, por lo que hay un punto tal que . Como no queda fijo, no puede estar en la línea . Como para todo en se cumple que
tenemos, por la proposición 14, que es una línea perpendicular la línea que pasa por y , cortando a dicha línea en el punto medio entre y . Es decir que se trata de una reflexión en torno a la línea .
Notas
[editar]F. Teoremas de Sylow
[editar]En este apéndice, obtendremos algunos de los resultados más importantes de la teoría de grupos finitos, uno de los cuales es una forma más débil del recíproco del teorema de Lagrange. Éste será el primer resultado que obtendremos.
Teorema 1 (Primer teorema de Sylow): Sea un grupo y un numero primo. Si divide el orden de , entonces tiene un subgrupo de orden .
Demostración: Por inducción sobre . Para se cumple, pues en ese caso ninguna potencia de un número primo divide a . Supongamos el teorema cierto para todo grupo de orden menor que . Supongamos que . Para todo , , y si divide a para algún , entonces la hipótesis de inducción nos da un subgrupo de de orden y el teorema es cierto. Si no divide a para ningún , entonces debe dividir a para todo no contenido en , y así divide a , donde la suma recorre las clases de conjugación de más de un elemento. Entonces la ecuación de clases
nos dice que divide a , y sabemos que, al ser abeliano, este contiene un elemento de orden . Ya que , es normal en , y podemos formar el grupo cociente , el cual es de orden divisible por (pues ). Aplicando la hipótesis de inducción, tiene un subgrupo de orden que por el teorema de correspondencia es de la forma para algún subgrupo , y .
Así, por ejemplo, el grupo alternado de orden tiene subgrupos de orden 2, 4, 3 y 5, y el grupo alternado de orden tiene subgrupos de orden 2, 4, 8, 3, 9 y 5, pues todos estos números son potencias de números primos que dividen al orden de cada grupo.
En particular, tenemos el
Corolario 2 (Cauchy): Si es un grupo y es un número primo divisor del orden de , entonces tiene un elemento de orden .
La formulación de los resultados restantes que obtendremos en esta sección se hacen en términos de la definición siguiente.
Definición. Sea un grupo y un número primo. Si es un grupo de orden y divide a y no divide a , entonces se dice un -subgrupo de Sylow.
Por el teorema de Lagrange, si es un -subgrupo de Sylow, entonces no hay un -subgrupo de orden mayor que el de , pues el orden de éste no dividiría al orden de , y por ello no puede ser un subgrupo de . Por lo tanto, un -subgrupo de Sylow es un -subgrupo maximal. Por el primer teorema de Sylow, un grupo siempre tiene al menos un -subgrupo de Sylow para cada primo , si bien es posible que éste sea trivial (cuando es la mayor potencia de que divide al orden del grupo). Notemos que si es un -subgrupo de Sylow de , entonces es también un -subgrupo de Sylow, puesto que este subgrupo es la imagen de por el automorfismo interno dado por . En consecuencia, un -subgrupo de Sylow es normal en si y sólo si éste es el único -subgrupo de Sylow de .
La demostración del segundo teorema de Sylow que daremos aquí depende del lema siguiente.
Demostración: Sabemos que es la unión disjunta de las órbitas (), y es la unión de las órbitas de un sólo elemento, de modo que
pero para todo , luego divide a y con esto
Teorema 4 (Segundo teorema de Sylow): Sea un grupo finito y un número primo divisor del orden de . Si es un -subgrupo de Sylow, entonces todo -grupo está contenido en algún para cierto . En particular, cualesquiera dos -subgrupos de Sylow son conjugados.
Demostración: Sea un -subgrupo de (no necesariamente de Sylow) y un -subgrupo de Sylow. El subgrupo actúa sobre el conjunto de clases laterales por medio de traslación izquierda, y por el Lema 3 sabemos que , pero como no divide a , debe ser , luego es no vacío y existe al menos un tal que para todo , lo que equivale a , luego . Si es un -subgrupo de Sylow, entonces , lo que implica .
Teorema 5 (Tercer teorema de Sylow): Sea un grupo finito, un número primo y el conjunto de todos los -subgrupos de Sylow de . Entonces y divide a .
Demostración: Sea un -subgrupo de Sylow y consideremos la acción de sobre por conjugación. Por supuesto , y si es otro -subgrupo de Sylow tal que , entonces , por lo que y son también -subgrupos de Syolow de , y por el segundo teorema de Sylow, son conjugados en , pero al ser normal en , debe ser . Por lo tanto , y el Lema 3 nos da . Puesto que se obtiene conjugando por cada elemento de , y puesto que el número de subgrupos conjugados de es , tenemos , el cual divide a .
- Álgebra Abstracta
- Operaciones (Matemáticas)
- Estructuras Algebraicas
- Matemáticas Universitarias
- Grupo (matemáticas)
- Homomorfismo de Grupos
- Subrupos
- Grupos Cíclicos
- Grupos Generados
- Clasificación de Grupos Finitos
- Divisibilidad
- Polinomios
- Cuerpos
- Dominios de Integridad
- Páginas que utilizan un formato obsoleto de las etiquetas math




































































































































































![{\displaystyle \mathbb {Q} [{\sqrt {5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5691f5e84ebcf23acbd458f90f57c0945549be8c)




















































































































![{\displaystyle \scriptstyle {\begin{matrix}f_{0}={\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}}&f_{1}={\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}}&f_{2}={\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}}\\[5mm]f_{3}={\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}}&f_{4}={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}&f_{5}={\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a7765f931baee5ba3d84b74b0504330b2554ccd)





![{\displaystyle {\begin{array}{lcl}{\begin{bmatrix}a&b\\c&d\end{bmatrix}}+{\begin{bmatrix}x&y\\z&w\end{bmatrix}}&=&{\begin{bmatrix}a+x&b+y\\c+z&d+w\end{bmatrix}}\\[5mm]{\begin{bmatrix}a&b\\c&d\end{bmatrix}}\cdot {\begin{bmatrix}x&y\\z&w\end{bmatrix}}&=&{\begin{bmatrix}ax+bz&ay+bw\\cx+dz&cy+dw\end{bmatrix}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6db3d1bc208597b2e6255cff198b7c2baa29f7f9)


















![{\displaystyle [x]=\{0,2,-2,4,-4,\dots \}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6392314521f6f60e772e1906eb89e2fe4e40e82)
![{\displaystyle [1]=\{1,-1,3,-3,\dots \}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d710299d1dcce072d8646e17548987fa2418aba)
![{\displaystyle \mathbb {Z} _{2}=\{[0],[1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc8cfe8b8eb99225795b2ede7a00a2732ddb71d7)
![{\displaystyle [0]=\{0,\pm 5,\pm 10,\pm 15,...\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a24089c9f6590ac9f69f989015470ab2cac21c33)


![{\displaystyle [1]=\{1,6,-4,11,-9,16,-14,....\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3b1a1fb001daf7714b558abf11d387fdfe1d3c)
![{\displaystyle [2]=\{2,7,-3,12,-8,17,-13,...\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ce8cb4beef375eabb78a3f0901b777b2530bd9)
![{\displaystyle [3]=\{3,8,-2,13,-7,18,...\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48f67419272ac639f1290125a2513d6b69218266)
![{\displaystyle [4]=\{4,9,-1,14,-6,19,...\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0420114515d6ce7048b1c7b0772dce307fa47ef)
![{\displaystyle [5]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38506b28c9fe3c535f3a2fecdda7448ad30477c8)
![{\displaystyle [6]=[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3516bebb85dd9a1bfcb74dacce27c3fd973ea297)
![{\displaystyle \mathbb {Z} _{5}=\{[0],[1],[2],[3],[4]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1177e3409ff2b24d68f06487ed3f2a51226a7f3)
![{\displaystyle [x]+[y]:=[x+y]\qquad [x]\cdot [y]=[x\cdot y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f61da45bbb8869a4e75fa08a15a178cef8f0cd0)










![{\displaystyle [a]=[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/410d2187c04d4e54d4ccec24556a76fd427a93aa)
![{\displaystyle [c]=[d].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/220bee6505785eba8fbdd1839b4a7e0b4f8f6bc7)
![{\displaystyle [a+c]=[b+d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19b2c98aa9cf6b7e2ad46ad8eb5ff501a1fe6401)
![{\displaystyle [ac]=[bd].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09d99b437304070b1e9b5ff3cf4cba05582bf62)
![{\displaystyle {\begin{array}{rcl}[a]+([b]+[c])&=&[a]+[b+c]=[a+b+c]\\([a]+[b])+[c]&=&[a+b]+[c]=[a+b+c]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66721c23069586773e08fc5e29995ccf26479169)
![{\displaystyle [a]+[b]=[a+b]=[b+a]=[b]+[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2df1bff6884614b55f751c5b4d0aa32d6979e37)
![{\displaystyle [a]+[0]=[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759b67517d0c34e79838c0fc1dc63a893079d84)
![{\displaystyle [a]+[m-a]=[m]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6330d6c97e1c88500163279d01000105ff7b645b)
![{\displaystyle [m-a]=-[a].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a55b7855f0d57717965247078e5c75469e2da03c)
![{\displaystyle [a][1]=[a\cdot 1]=[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160bd73d29b48bddf3017f20dee68105edf1d505)

![{\displaystyle [2]\cdot [3]=[6]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35c3006e53918e3eb9f6db6337a3cfa7fdd42ec0)


![{\displaystyle \mathbb {Z} _{[}13]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3100c27af68b936dbc46e9739e8a5db73c25578)
![{\displaystyle x^{2}+[3]x+[15]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2c29590e2dd532392e13a63dec65bdf19da3da8)







![{\displaystyle [x]+[y]=[x+y]\quad {\text{ y }}\quad [x]\,[y]=[xy]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3261cf65f214075aa75e30f417cccdcb6e89addc)

![{\displaystyle [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)

![{\displaystyle {\begin{array}{lrcl}&ax+py&=&1\\\implies &[ax+py]&=&[1]\\\implies &[ax]+[py]&=&[1]\\\implies &[a]\,[x]+[p][y]&=&[1]\\\implies &[a]\,[x]&=&1.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0efb58c05449e2785213ae804260f1b07c2b10c6)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)







![{\displaystyle [x],[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5915b430f4a1abc6149b0e2ad009f74abf0d39f7)
![{\displaystyle [x][y]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6db3f45781fdb0c23621f305e491c4f8d8efd28d)











































































































































































































































































![{\displaystyle \nu (x+y)=[x+y]=[x]+[y]=\nu (x)+\nu (y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3db1bf282acb8b4f2aef242894b4069d9d36148b)











































































































































































![{\displaystyle <[2]>}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4391d840f4a9ebcc1e2e6bc76af5987d12a070)
![{\displaystyle <[3]>}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a57821533d9c78fb615e78170dcdcd89ba0fc0c)














































![{\displaystyle [3]{\text{ y }}[4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85480d22d7ab5910d43756eb94a27d43fa3bb232)











































































![{\displaystyle det(M_{x})=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/394a6a31bcb662d2323520433510cf3dd7f5cf07)
![{\displaystyle \det(M_{x}A)=[x]\det(A)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47cdd30d262fcef63b576f8671c0352b1be831e3)





























![{\displaystyle {\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c|c|}{\text{elemento}}&[0]&[1]&[2]&[3]&[4]&[5]&[6]&[7]&[8]&[9]&[10]&[11]\\\hline {\text{orden}}&1&12&6&4&3&12&2&12&3&4&6&12\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1e618804d2e6947d364c71dd582847c799c021f)















![{\displaystyle o([3])=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4768d713b53174175eeffdefb21c145d6b231365)
![{\displaystyle 4\cdot [3]=[12]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b51985aa448022d54c82f69c7a9391f84f2aac)
![{\displaystyle 1[3]=[3]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47b7644bd0e907ada9e3f8c766538fb288dc3a6b)
![{\displaystyle 2[3]=[6]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3455755a0b4f4956eaafe2fe9bab3b04b9f84de)
![{\displaystyle 3[3]=[9]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/975a6feecf4bba1d93dd074cfbc3eea28925c33f)

































































































































































































































































![{\displaystyle \mathbb {Z} _{30},\quad [10].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f006f9104a286d8aca01551fdefdcc69207a566)
![{\displaystyle \mathbb {Z} _{50},\quad [12].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1620c9561924c7811d9024d33a7596a485547685)
![{\displaystyle \mathbb {Z} _{50},\quad [11].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a547ec964e18ec6f03b6c1f38bf9c6a877b8b46)






































![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)
![{\displaystyle [x,y]:=xyx^{-1}y^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e110bfa4015dd8bd969254ae1fe0dde25ed02c85)













































































































































































































































































































































































































![{\displaystyle A=\{[2],[4],[5]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f34655b65b462b5e92004ea85bcfa7566e09896)
![{\displaystyle B=\{[1],[7]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c85026591bd7ab898a8d5e84401c828d9c8d073e)

















































































![{\displaystyle [x]_{H}\subset [x]_{K}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94ba1babc2eff3821db8c0edb385e09e368c9607)














![{\displaystyle f(x)=([x]_{r},[x]_{s}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9af3ca8adb5b4ee77e0822fa70ed0642a991ecff)
![{\displaystyle {\begin{array}{rcl}f(x+y)&=&([x+y]_{r}[x+y]_{s})=([x]_{r}+[y]_{r},[x]_{s}+[y]_{s})\\&=&([x]_{r},[x]_{s})+([y]_{r},[y]_{s})=f(x)+f(y),\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5babf5087b53b17090cc9f19f1fe72b3e7589562)
![{\displaystyle f(x)=([0]_{r},[0]_{s}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2107029f2d4e7e34328445a2c8c511bda5d2e76f)



![{\displaystyle ([0]_{r},[0]_{s}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04878b732d0add9486f84d510134786a6fecaf6)










![{\displaystyle \phi ([x]_{n})=([x]_{n_{1}},[x]_{n_{2}},\dots ,[x]_{n_{k}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f02993f2f83a036118ba794eed5276f145ef2e3)


![{\displaystyle [x]_{n}=\phi ^{-1}([a_{1}]_{n_{1}},[a_{2}]_{n_{2}},\ldots ,[a_{k}]_{n_{k}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e4d5ad8439afca7c94e142503465687a0a529d)



![{\displaystyle H=\{[x]\in \mathbb {Z} _{mn}^{*}:x\equiv 1{\pmod {n}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea3758a563fff75789823956d1398889da392390)
![{\displaystyle K=\{[x]\in \mathbb {Z} _{mn}^{*}:x\equiv 1{\pmod {m}}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80085c7e1b611f5edf7e35f723da5bfb0a2f3a36)






![{\displaystyle H\cap K=\{[1]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3794d2a4bf21eeb158e776e6c296f989b66c2dae)





![{\displaystyle [h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/495b120a49645594b0e587207059eb2391ecc8ac)
![{\displaystyle [k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9278f059ccf89ce18a2e393c1301a934faec8d5d)





![{\displaystyle [x]_{mn}\rightarrow [x]_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc1d986aac60a4c93d672ec6f871707f17db446c)

![{\displaystyle f(x)=[x]_{m}=1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9464dadd5ac5b5aabc63a3a600cfd65f536675)

![{\displaystyle [x]_{m}=[a]_{m},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a932daebcaac8c5000c05693b56c32101f841745)






































































![{\displaystyle {\overline {f}}([x])=f(x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5653698b4e5927f64cf30af2877287a189b80da)












![{\displaystyle x\mapsto [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a07b95c49afdb5a84f26120657148e94c94a69be)





















































































































































![{\displaystyle [G:C(a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39794b76393e9644f74f878827d168845f5d3a42)
![{\displaystyle |{\mathcal {C}}(a)|=[G:C(a)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2e07361b73be18120e96da0e0f475118fcc695f)
![{\displaystyle |G|=|Z(G)|\quad +\sum _{a\in D\setminus Z(G)}[G:C(a)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7477ec7e2e46115f29a2b7578b8bbf8c7b67b8)



















![{\displaystyle [G:\langle x\rangle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea56b5a2f0b3edb80f78829f7e13877ad34cd503)




















![{\displaystyle |G|=|Z(G)|\quad +\sum _{a\in D\setminus Z(G)}[G:C_{G(a)}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86ef8e5c9ccef57ece9fb1b3d504d171302e716c)

![{\displaystyle [G:C(a)]=|G|/|C(a)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8713b7a6beb65e84202b5b30ed41263c5b3d3)



![{\displaystyle |G|=|Z(G)|+\sum _{a\in D\setminus Z(G)}[G:C(a)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55dbfe42903ed25d717ee739fed0ca6bb8432f48)
































































































































































































![{\displaystyle k[G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a13dacf8d6ff682a6b5d59e84f93e589cba3fa1)






























![{\displaystyle A=\mathbb {Z} [i]=\{a+bi:a,b\in \mathbb {Z} ,i^{2}=-1\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca38dc5461f11f4bbf599df4c9fabe4b207a0ba1)



































![{\displaystyle D=\mathbb {Z} [{\sqrt {-5}}]=\{a+bi{\sqrt {5}}:a,b\in \mathbb {Z} ,\quad i^{2}=-1\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa857891cecae0cba096e5dc865e3294e30e142)













































![{\displaystyle D=\mathbb {Z} [{\sqrt {-m}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9340dfb0447bd26e31991e3de396ab9c4d8a0fc)

![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)




![{\displaystyle \mathbb {Z} [i].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03900897cdf515bbbc52879377653a871b9efc06)














































![{\displaystyle p,2p,,\dots ,(p-1)p,[p*p,(p+1)p,\ldots ,(p^{2}-1)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ca318b0b05d31e7e8f2cc9974187f1564ba2cc5)


![{\displaystyle [p].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f877f891f90f682792de5b93e82a972696151921)




![{\displaystyle [rp]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d76da7ca9dab913f4e8e3fe8ef98fff61a43728f)
























![{\displaystyle I=\{x:[x]\in J\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5011d7e399a8817987c3ac175cae300ec28e0e7)





























![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




![{\displaystyle {\begin{matrix}{\text{a. }}&[ca,cb]=[a,b]\quad &\quad &{\text{b. }}&[0,b]=[0,1].\quad &\quad &{\text{c. }}&[a,a]=[1,1].\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6234983ec62b8358ff996bd9806f8cdc69faca5d)

![{\displaystyle [0,b]=[0\cdot b,1\cdot b]=[0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f353c3811d1ff811310eee5a454d686c2dc0f542)
![{\displaystyle [a,a]=[1\cdot a,1\cdot a]=[1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/627be1112c0f11ddc0cb09018c88859131e8bbea)
![{\displaystyle \quad [a,b]+[c,d]=[ad+bc,bd].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28b8fb43154a6d41eca441d21573d11af8ee01a8)
![{\displaystyle \quad [a,b]\cdot [c,d]=[ac,bd].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/512e94edc09f0e497910d8ce8a45a8137b01a09e)


![{\displaystyle [a,b]+[c,d]=[a',b']+[c',d']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95359a60c130ee14c778f5f3afc6b7292f36bb40)
![{\displaystyle [a,b]\cdot [c,d]=[a',b']\cdot [c',d'].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9809273a4e8bc4ba3fe2c5837551bb8b4f617369)
![{\displaystyle [ad+bc,bd]=[a'd'+b'c',b'd'].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/259e927218e3debb4a5aa79e52c0e402b272a376)

![{\displaystyle [ac,bd]=[a'c',b'd'].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cf69e236d2bcf16281b5d4a5b13fdf6f0451221)



![{\displaystyle [a,b]+[0,1]=[a\cdot 1+b\cdot 0,b\cdot 1]=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b137c32a7a2bd411157387a19ad43c5307cf16d4)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle [a,b]+[-a,b]=[ab+b(-a),b^{2}]=[0,b^{2}]=[0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43173beedf4bdc5e39d0ab7074518e2f89d4890f)
![{\displaystyle \alpha =[a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612a26b7f7438ec13b379d07e752e7964efbd085)
![{\displaystyle \beta =[c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f637aebafdd78321279041fc342a2b61efbacec)
![{\displaystyle \gamma =[e,f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceeb14c736cfe0d1228da733f308f61577178d07)
![{\displaystyle {\begin{array}{rcl}\alpha +(\beta +\gamma )&=&[a,b]+[cf+de,df]\\&=&[adf+bcf+bde,bdf]\quad {\text{y}}\\(\alpha +\beta )+\gamma &=&[ad+bc,bd]+[e,f]\\&=&[adf+bcf+bde,bdf]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d257e106831bd83ac2eb8c7fd67a03a05beef30c)

![{\displaystyle {\begin{array}{rcl}\alpha \cdot (\beta \cdot \gamma )&=&[a,b]\cdot [ce,df]=[ace,bdf]\quad {\text{y,}}\\(\alpha \cdot \beta )\cdot \gamma &=&[ac,bd]+[e,f]=[ace,bdf],\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d00664ec1fd90ab63070e14207143d462b424f8)
![{\displaystyle [a,b]\cdot [1,1]=[a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0b994a727e0663e42f9fb4e86142ebe8dbaf502)
![{\displaystyle [1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a93c33bf544dd008f34d152345c97525bda7fe8)
![{\displaystyle [a,b]=[0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/307cf556999b4e354456f8f61851377172a1a639)

![{\displaystyle [a,b]\neq [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02c9d8dcb19297269294a5a39da67f049cd63e1)

![{\displaystyle [b,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3015146003c7dab01d939e34e07159fa9604bc3)
![{\displaystyle [a,b]\cdot [b,a]=[ab,ab]=[1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c02331e5a23eb5081ee5413b1bc8f6b56361e292)
![{\displaystyle {\begin{array}{rcl}\alpha \cdot (\beta +\gamma )&=&[a,b]\cdot [cf+de,df]=[acf+ade,bdf]\quad {\text{y,}}\\\alpha \cdot \beta +\alpha \cdot \gamma &=&[ac,bd]+[ae,bf]=[abcf+abde,b^{2}df]\\&=&[b(acf+aed),b(bdf)]=[acf+aed,bdf]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4dc5e3bcaef227a3aa03b2ca187fffee31166d)

![{\displaystyle [a,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec86c99378fcefca03faf5139c7922106015937)
![{\displaystyle [a,1]=[b,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3ec477d76be1c9b55e553171c555a4a35615791)


![{\displaystyle {\begin{array}{rcl}f(a)+f(b)&=&[a,1]+[b,1]=[a\cdot 1+1\cdot b,1\cdot 1]=[a+b,1]=f(a+b)\quad y\\f(a)f(b)&=&[a,1]\cdot [b,1]=[ab,1]=f(ab).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fe8c24d101b4bc4706b73e0ee3060ed9015b260)
![{\displaystyle f(1)=[1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d682f1a5f3bc1236ce33ad71d31cfa43831c79a)
![{\displaystyle [a,b]=[a,1][1,b]=a[1,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb3f6e09556730a786453d927057e0b1a79f6dd6)
![{\displaystyle [1,b]=[b,1]^{-1}=b^{-1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/583cd19aa374d746518a46a8b65372ab98f9f4ea)
![{\displaystyle [a,b]=ab^{-1}={\frac {a}{b}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34130d3f76d33ff5b83acaf03da9ceeb4af85798)















![{\displaystyle \mathbb {Z} [{\sqrt {13}}]=\{a+b{\sqrt {13}}:a,b\in \mathbb {Z} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ca79db000bc1c1064488a2d04f2807c4e2c7545)
![{\displaystyle K=\mathbb {Q} [{\sqrt {13}}]=\{x+y{\sqrt {13}}:x,y\in \mathbb {Q} \}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5e225d98181be62f34c1995268aeae01a89d5c)


![{\displaystyle D=\mathbb {Z} [{\sqrt {m}}]=\{x+y{\sqrt {m}}:x,y\in \mathbb {Z} \},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6a4b16064311afc6e2f09e3df9e02eb265bd96)



![{\displaystyle D=\mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3e5294b697d24ab1922b499f79ea03d554d4c8d)




![{\displaystyle D=\mathbb {Z} [{\sqrt {2}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/206da139d4eac1ccd9593133fda50f9466851017)

![{\displaystyle E=D[{\sqrt {3}}]=\{\alpha +\beta {\sqrt {3}}:\alpha ,\beta \in D\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/568f145efbb117087a142c62421a9677c9200e12)

























































































![{\displaystyle \mathbf {A[X]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/71525b41111499ead0202af72b200b6fe36a9cac)

























![{\displaystyle A[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/090f400ff9885a71ac632850c53a44200e1ec4ab)

























![{\displaystyle A[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40abd94a808a2369931fac9811cbd1cbdd44497d)















![{\displaystyle B[X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb8d20f358c84716b0bde2483ef711ff9c263011)
![{\displaystyle \mathbb {Z} [X]<\mathbb {Q} [X]<\mathbb {R} [X]<\mathbb {C} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/536fe4e748fb166d462fda15e8625775e8ef08ee)
![{\displaystyle A[X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0195132abd0b4f9fb108e9c38838f3b60f33b0)

![{\displaystyle A[X][Y],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09e9e94504b25d608519cdc75f420532f1b8c5a3)
![{\displaystyle A[X,Y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7026fba64721ea7dee3d0299e1016d460d35afc0)
![{\displaystyle A[X,Y,Z]=A[X,Y][Z],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af3eb9fcab8231f6ff7862c18fc6628165681c12)

![{\displaystyle A[[X]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6859aedb35d49362a6fea7725d7cc9c2f6301fd2)











![{\displaystyle \mathbb {Z} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dff5f5cc8f92c9047be4851007baca114ceb3e2)








![{\displaystyle \mathbb {Z} _{3}[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd48ae85f99fd1d44940cf84dc926674947e494)




![{\displaystyle \mathbb {Z} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a538d203a057d4c604f799c28e9a7be410fdcac)



![{\displaystyle \mathbb {Z} [[X]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d405ff4b301e3592ca0e972a830af696cda5418)


![{\displaystyle \mathbb {Q} [[X]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb23a5adf83c041dc5b999b72165576981ea3776)



![{\displaystyle D[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa482bb7dcd759ae8e7e38fa47bea024feb50892)

























![{\displaystyle {\begin{matrix}a.&{\dfrac {X}{X^{3}+2X}}.&b.&{\dfrac {X^{3}-5X^{2}+6X}{X^{2}-2X}}.\\[2mm]c.&{\dfrac {X^{4}-1}{X^{2}-1}}.&d.&{\dfrac {X^{6}-64}{X^{3}-8}}.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74aa408b190ff23d8704c36619210703a5137403)
![{\displaystyle A[[X]],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd4d6006edc92c7972179bb79486fe9322a785bf)

















![{\displaystyle {\rm {{ev}_{\alpha }:A[X]\longrightarrow B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0631a96a629363b84727eab52b34074e08e8746d)

![{\displaystyle {\widetilde {\phi }}:A[X]\longrightarrow B[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71d658b9ee6a9faef3675566b870ce5aa3a9a17f)



![{\displaystyle B[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597e929ed0771e50e046a31b2e6e378fe24c3d9b)





![{\displaystyle x\mapsto [x].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e914ebc3c9d5d3224a0b218c8b7ea6df8a61e16d)




![{\displaystyle B=A[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b428c0eeb836b1999c17217f0a4457b911b6a6d)




















![{\displaystyle \mathbb {Z} [X]<\mathbb {Q} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6507565648739ba5118a40fade8c9545334a667)











![{\displaystyle \mathbb {Q} [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a347aa1f28466fd55bc276972be2d6e49cc926f)


![{\displaystyle 1,\ 2,\ {\sqrt {3}},\ 2+{\sqrt {3}},\ 1+{\sqrt[{3}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c2e37de07be5e6f6a9cd726637a2e1af8dcaba)
![{\displaystyle {\begin{matrix}a.&{\sqrt {2}}.&\quad &b&3-{\sqrt {7}}.\\c.&{\sqrt {3}}+{\sqrt {2}}.&\quad &d.&{\sqrt {5}}+{\sqrt[{3}]{2}}.\\e.&{\dfrac {1+{\sqrt {-3}}}{2}}.&\quad &f.&{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}.\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/249ee2fbd96ed67ca2d3cc1bb432a6001d820ff2)

![{\displaystyle {\widetilde {f}}:A[X]\longrightarrow B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a69bb2f2f7e3da1fcbe1e7f875c907b1ac2bafc3)


![{\displaystyle \mathbb {R} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16d740527b0b7f949b4bf9c9ce004134bb490b68)





![{\displaystyle \varphi :A[X]\longrightarrow A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d09d10d7e804fb0c06c9092c33fa1b66b8af787)





![{\displaystyle F[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26dc049157db08b423b1c6916eba0c81b1bdc18b)



































![{\displaystyle k[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4013b934bf67b95971a82ebabab1b56dafd88835)
![{\displaystyle \mathbf {k} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22af1b7286e4bd307bd8969d447694f1cfb481be)
![{\displaystyle k[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4d0e89263c5739d911e9ef04e374f746a37be6c)
![{\displaystyle k[X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8369e412546aa50876eae8d1baaac3c1b3528cd)











![{\displaystyle J=\{xf+yg:x,y\in k[X]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52dc5599f4032bef4836de9c0a81b9be3f13e407)



























![{\displaystyle \mathbb {Q} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f611a32bc84287517e9f4b283ac998c0394479)
![{\displaystyle \mathbb {Z} [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/451c1a17c145340a300e8bd4f1827c9de1606dce)







![{\displaystyle A=k[X]/<f>.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f809cd1335dd536d93b7caeb51e8f8fa97390ff)
![{\displaystyle [g]\neq [0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb6995b544d679a785dd621ac5194222bcb85368)



![{\displaystyle [a][g]+[b][f]=[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00737433422986ec24a730bfb1201017f5420df6)
![{\displaystyle [f]=[0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7d7d7f4b7481ac7ae3179f189371ac48c9d716)
![{\displaystyle [a][g]=[1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba2263b77a66d550f32e23513b6c666b92b18fd)
![{\displaystyle [g]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6545341f409fd77429f02ba8bb88e4445bc2002a)
![{\displaystyle k[X]/<f>}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c030fe77807931d9376d16aae5c112f31e92d14d)
![{\displaystyle k\subset k[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531c3f272678b7550f4b3a98effd7e5464be0e19)
![{\displaystyle [\alpha ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e09d1dcb41984c30930c3b235d1d81b1577aaa3f)
![{\displaystyle k[X]/<f>,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/408282b4df7efd31f11a83eceb7eab7212b05cd9)
![{\displaystyle [\alpha ]=[\beta ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3264e313f12b23daa4a12ebee3b5eb61e13a9fc9)
![{\displaystyle [\alpha -\beta ]=[0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85eeceb25a55666871996a657feec8895a9dee19)


![{\displaystyle k\subset k[X]/<f>,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41565af4bedafc7b22d3e64a6378e0aaffdbcebd)
![{\displaystyle \theta =[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b5fe5dc27b85eb792124b6d9dfc9e8fc90b4128)
![{\displaystyle k[X]/<f>.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82fa7d7026568f16918b301c5eb0d8e5dfe33e35)

![{\displaystyle [0]=[f]=\sum _{i}[a_{i}][X]^{i}=\sum _{i}a_{i}\theta ^{i};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635f82f0f7047cf8b51b7d3a7985b134ca253ec5)
![{\displaystyle f\in k[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aac9766795342d43b6954b69741a2d175f5b5106)

















![{\displaystyle \mathbb {Q} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42555484bfcbd23f412c81e7cef86c9b5d08aba1)


































































![{\displaystyle \mathbb {Z} _{2}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4f1592669b3b33c43c57c6d90c4b4c590d607e8)
















































![{\displaystyle D[X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f632b0285995fb3493073e5e50813167be6cc2de)

































![{\displaystyle {\begin{array}{rcl}(fg)'&=&(\sum _{k=0}^{m+n}\sum _{i+j=k}a_{i}b_{j}X^{i+j})'\\&=&\sum _{k=0}^{m+n}(\sum _{i+j=k}a_{i}b_{j}X^{i+j})'\quad {\text{ por e)}}\\&=&\sum _{k=0}^{m+n}\sum _{i+j=k}(a_{i}b_{j}X^{i+j})'\quad {\text{ por e)}}\\&=&\sum _{k=0}^{m+n}\sum _{i+j=k}a_{i}b_{j}(X^{i+j})'\quad {\text{ por d)}}\\&=&\sum _{k=0}^{m+n}\sum _{i+j=k}a_{i}b_{j}[(X^{i})'X^{j}+X^{i}(X^{j})']\quad {\text{ por f)}}\\&=&\sum _{k=0}^{m+n}\sum _{i+j=k}a_{i}b_{j}(X^{i})'X^{j}\\&&\quad +\sum _{k=0}^{m+n}\sum _{i+j=k}a_{i}b_{j}X^{i}(X^{j})'\\&=&f'g+fg'.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8837627bd6688ce65f652ab610d3457b07fbaff8)


















![{\displaystyle u=X^{p}-a\in \mathbb {Z} _{p}[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c2c1e9e96d44a5720181f451c1b8066b3c22a9)





![{\displaystyle {\begin{array}{rcl}x^{4}-5x^{2}-3x+18&=&\quad 94x^{3}-15x^{2}+10x-3)({\frac {1}{4}}x-{\frac {5}{16}})+(-{\frac {35}{16}}x^{2}+{\frac {7}{8}}x+{\frac {273}{16}})\\[2mm]4x^{3}-15x^{2}+10x-3&=&\quad (-{\frac {35}{16}}x^{2}+{\frac {7}{8}}x+{\frac {273}{16}})(-{\frac {64}{35}}x+{\frac {1072}{175}}+({\frac {896}{25}}x-{\frac {2688}{25}})\\[2mm]-{\frac {35}{16}}x^{2}+{\frac {7}{8}}x+{\frac {273}{16}}&=&\quad ({\frac {896}{25}}x-{\frac {2688}{25}})(-{\frac {125}{2048}}x-{\frac {325}{2048}})+0\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/690d75202f4a3804fb89e5bbbaa5e769c01b14a7)












































![{\displaystyle \mathbb {Z} _{p}[X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af98689c91522d90e0279dce19b8ee206edc2b6)




![{\displaystyle \eta :A[X]\longrightarrow A[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d0af725d2c0b7752c0a465fba54d82b066625ac)

















































![{\displaystyle f\in D[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a6feacfab8d0de81922c91d23fcfcd3f595c38)

























































![{\displaystyle D[X]:}](https://wikimedia.org/api/rest_v1/media/math/render/svg/330696af5a931798f814573780060022ba63b937)




































![{\displaystyle D[X,Y,Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de32305b84e7067c6bdf19185d65cf8af9767082)


![{\displaystyle \mathbb {Q} [X,Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3c2b8ce5462578c7280b2ad496801b681b9393d)
![{\displaystyle \mathbb {Q} [X,Y]=\mathbb {Q} [Y][X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03f74d5926efdd92ad383a9eb7d39bd7f802d74)
![{\displaystyle \mathbb {Q} [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89f74c5efaab5e8b7711d0e18399211934cf73c)
![{\displaystyle D=\mathbb {Z} _{2}[Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cff49a6d56ee935b9349bff38f8fefb64f876b4)






































![{\displaystyle \phi _{m}:\mathbb {Z} [X]\longrightarrow \mathbb {Z} _{m}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eb81f5c5717d2057e8809ee6585bfdb8a9c2ab0)
![{\displaystyle \phi _{m}(f)=\sum _{i}[a_{i}]_{m}X^{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b670e2a86a2032384ec2bb9efd172d5bb922ca7d)


![{\displaystyle Z_{m}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579f86712c4deece609c70d65131dd15e6c0df16)



































![{\displaystyle \mathbb {C} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6c0e47242946827f33aad1803d66106d2f0307e)





![{\displaystyle \Phi _{d}(X)\in \mathbb {Z} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1256919c712649f57d5c54df1dfdd42b0c3bd038)




![{\displaystyle f\in \mathbb {Z} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0cc39aaa62a3915bbecd714f9e52c2beb2dd8e2)















































![{\displaystyle {\sqrt[{n}]{a}}\zeta ^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e67b0a11857c841fc1890605680d113273d8626)























![{\displaystyle {\begin{array}{lcl}{\dfrac {a+b\alpha }{c+d\alpha }}&=&{\dfrac {a+b\alpha }{c+d\alpha }}\cdot {\dfrac {c-d\alpha }{c-d\alpha }}\\[3mm]&=&{\dfrac {(ac-bdm)+(ad+bc\alpha )}{c^{2}-d^{2}m}}\\[3mm]&=&{\dfrac {ac-bdm}{c^{2}-d^{2}m}}+{\dfrac {ad+bc}{c^{2}-d^{2}m}}\alpha .\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2efe03f76f4c8ffd61246de57bd275d1c30d63)











![{\displaystyle [f]_{m}=\{g\in k{X}:g\equiv f{\pmod {m}}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8c4e8dab28ac138349dfeaaa689dcc3d6c6df84)


![{\displaystyle k[X]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7528169f03862ee8a2e7fb47381117b2473ef6d5)
![{\displaystyle k[X]/\langle m\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8e9198a56bc26d15a4ffbea929c8bf963e6aea9)




![{\displaystyle {\begin{array}{rcl}[h]&=&[\sum _{i=0}^{n-1}a_{i}X^{i}]=\sum _{i=0}^{n-1}[a_{i}X^{i}]=\sum _{i=0}^{n-1}[a_{i}][X^{i}]=\sum _{i=0}^{n-1}a_{i}[X]^{i}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a2e900e152ffc6b79eeaa9308ab921cf1c44205)
![{\displaystyle E=k[X]/\langle m\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8af6c15b6c801f7671be85fd6c6a4ae391dc9ef)
![{\displaystyle [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)
![{\displaystyle [h]\neq [0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268c7b6857cc903e7ec4e70cc386a4ed05b51f69)




![{\displaystyle [f][h]+[g][m]=[1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae6cf2fd5fe4ca5ca5ac352b40ed632b5148344)
![{\displaystyle [m]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04e5df8dd175e6cbbc57f84235e5b8ec91c3b16f)
![{\displaystyle [f][h]=[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6604dd69f234fc2a53f3dba77e9c081a9e4b1837)
![{\displaystyle m([X])=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/369d7530ed744911215b355c99b6e3f6426f1074)



![{\displaystyle K=k[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92af59724403e330afc8d8b9e92eadc3a33ca474)
![{\displaystyle [0]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b38ec385a3f0604a33b1c8a3905402f88b385d7)
![{\displaystyle [1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6606ef0a0281091619c74fe539c123cf6001ce54)
![{\displaystyle [X+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ab730ac221279f5e47e5df6b161b121b56424a)
![{\displaystyle 0=[m]=[X^{2}+X+1]=[X]^{2}+[X]+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fae1f33760d9e32a4d956a11a1d8ef9b121c7c3b)
![{\displaystyle [X^{2}]=[X]+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cb3aa9efa40f8433b02e7b4ca3fb7f3948743de)
![{\displaystyle [X][X+1]=[X]^{2}+[X]=[X]+1+[X]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edec2fcf10cb5ab23bee31a89537395249682917)











![{\displaystyle \alpha ={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b004957ace3903d27ea13a7d8013ce12e7869294)


![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
![{\displaystyle \omega {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8760a51aec3a8be3be7ac8e05719a1a7a06efa)
![{\displaystyle \omega ^{2}{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2911699e8a17b9af565dccd6758d598bae9d90)

![{\displaystyle \alpha =[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55fcccdec703ad4a778fc79d92b8c158d30a36f8)

![{\displaystyle K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb4d802ca5718a14dc961af8692f35cdfad169b)




















![{\displaystyle ev_{\mu }:k[X]\longrightarrow E}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8406b5fd5bc4e772ffcfb41e9884768446a9267e)



![{\displaystyle k[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/da568f82ff4be403aab27b61de3734e8f3163151)

![{\displaystyle Q({\sqrt {m}})=\{a+b{\sqrt {m}}:a,b\in \mathbb {Q} \}=\mathbb {Q} [{\sqrt {m}}]=\mathbb {Q} [X]/\langle X^{2}-m\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d18a0b5c7f5911d29406cbdc93f004eac7b44992)














![{\displaystyle \alpha =[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02c7c980af2791ce7ae4e2abf308afdae1ba2cc9)







![{\displaystyle {\begin{matrix}a.&[X^{4}].&&b.&[X^{8}].&&c.&[X^{n}],\quad n>0,{\text{ cualquiera}}.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4b61a29aa6be0f6c91b4faade912f533a3cf5e)



![{\displaystyle A=\mathbb {Z} _{2}[X]/\langle X^{3}+1\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c83d9942f2ae17876bf0298e0722268f4dc9d24c)










![{\displaystyle {\begin{matrix}a.&{\sqrt {7}}.&&b.&1/{\sqrt {7}}.&&c.&{\sqrt[{3}]{2}}.\\d.&3+{\sqrt {2}}.&&e.&{\sqrt {-5}}.&\ &f.&{\dfrac {1}{2}}+{\dfrac {\sqrt {3}}{2}}i.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec3d84d57435440b929c96908f6b9324a89dcf0f)









![{\displaystyle \mathbb {Q} [\alpha ]=\mathbb {Q} [\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe8fc62dee69b88c6cd64fbf97d61e1476ba343)
![{\displaystyle E=\mathbb {Q} [X]/(X^{2}+X+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac07e1f0a69e5153fd25a56be70f18371a974508)






































































































![{\displaystyle E=k[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/849c0fb17d8397b044f1754c22deb74abb8a2ceb)



![{\displaystyle \mathbb {Z} _{p}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de003d02e4e521633a0d25dcf88c18209500f160)


![{\displaystyle \mathbb {Z} _{p}[X]/I\cong F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/859b4e201f122ee6aa2137f340c0c6ff62f68ced)


![{\displaystyle F\cong \mathbb {Z} _{p}[X]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a2b33bc3da4e0ced71928b9a9fd2766cb8c173)

![{\displaystyle F\cong \mathbb {Z} _{p}[X]/\langle g\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a586bc861605d4f036d29f467b3913f9bbc4996)



















![{\displaystyle K_{f}=\mathbb {Z} _{p}[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/584993d5b346bce3de84220f9a1cc604d6df2814)
![{\displaystyle K_{g}=\mathbb {Z} _{p}[X]/\langle g\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fa5dd981407316089b1ba63933425ac93848268)
![{\displaystyle K\cong \mathbb {Z} _{p}[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/af082251201a05c463b72a82e76f0f8bb14404d4)
![{\displaystyle ev_{\alpha }:\mathbb {Z} _{p}[X]\longrightarrow E}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026213a109b11f3a2100b2796bd1bbc1a533d474)

![{\displaystyle \mathbb {Z} _{p}[X]/\langle f\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/79b697f4f64bf8a7635f7495371355a7fff68e82)






















![{\displaystyle \mathbb {F} _{p}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eded0c154aa847807d7f992fdf6db7eb5a73476)

![{\displaystyle \mathbb {F} _{p}[X]/\langle g\rangle \cong \mathbb {F} _{p}(\gamma )\cong \mathbb {F} _{p^{d}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d68d70796ae781e421a7024a418a585aca1661bb)
![{\displaystyle \mathbb {F} _{p}[X]/\langle h\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8be81148590f8dbbd3b3753cae877aa4a6435203)

![{\displaystyle \mathbb {F} _{p^{n}}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597587c4f74acbb4f32f400eac5083268ac1a2d3)
































![{\displaystyle A=\mathbb {F} _{3}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b808b8e1dfc44bc910696e4f54911fa2fe52a2b)





![{\displaystyle \mathbb {F} _{3}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952f4d959e33b576de39a3bbbff1dcbcc82a482b)
![{\displaystyle \mathbb {F} _{2}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8103d8dabb10f0607e27ff6068740418e81a5af4)
![{\displaystyle E=\mathbb {F} _{3}[X]/\langle X^{3}+2x+1\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/09303a9c7f1860da728bfeab7903b155b888db6e)

![{\displaystyle \mathbb {F} _{3}[X]/\langle x^{3}+2x+1\rangle =\mathbb {F} _{3}[\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95f2e349149b67fee414d0fbcbacc65ce7d91c1c)



![{\displaystyle \mathbb {Z} [m]=\{a+b{\sqrt {m}}:a,b\in \mathbb {Z} ,m{\text{ un entero que no es un cuadrado}}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c342bcc5e5d58d2dbf1c4687a140f84f97b6e3f)
![{\displaystyle \mathbb {Z} [i],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59ada2ccab5ac1f61c1a433445d58dea97a0c69d)












![{\displaystyle \mathbb {Z} [{\sqrt {-5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a37499ef27234d8a67a65932184280bb17301312)










































































![{\displaystyle \mathbb {Z} [X_{1},X_{2},X_{3},\dots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93a6fa668a07840eb2baccf17bc623a220dd280e)
![{\displaystyle k[X_{1},X_{2},X_{3},\dots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1bb73e2e018bef5071bb1e5fee1a84a2b62f82f)






![{\displaystyle D[X_{1},X_{2},\dots ,X_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f35d66756e77ce19f73578ed5a1c0e780f147b4)






































![{\displaystyle D=\mathbb {Z} [{\sqrt {2}}]=\{a+b{\sqrt {2}};A,b\in \mathbb {Z} \}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90c7ad2f35d63fc1baaecb1f8b74eb3db617ea79)






















![{\displaystyle D=k[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e665a7e8787f02a1c5424971dc5b85876d2af87d)




















![{\displaystyle \mathbb {Z} [\omega ]=\{a+b\omega :a,b\in \mathbb {Z} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b07a7e53e432294b39d5817fe4b604b8b98fcb6)




![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)

![{\displaystyle \mathbb {Z} [\omega ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a661e97c4c69834950b46ffb47fb19179829cd4e)

![{\displaystyle \mathbb {Z} [i]=\{a+bi:a,b\in \mathbb {Z} ,\quad i^{2}=-1\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb17abd228f727f3440b0d64eca1b5b2be0cfcff)












![{\displaystyle \tau =u_{1}+iu_{2}\in \mathbb {Z} [i].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e68d68e8173522a047bbc9ce26a83e683a8d9754)










![{\displaystyle \mathbb {Z} [I].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f733f72a20d7bec634428ed32848ae0cacd63c4)
![{\displaystyle \mathbb {Z} [I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17565a0b84424b8021910edbf00e4b955f73a822)




![{\displaystyle \mathbb {Z} [I],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd33964eb9fd904228c0115dd7f88f2dd955ca0d)


![{\displaystyle z\in \mathbb {Z} [I]{\text{ es una unidad }}\iff N(z)=1\iff z\in \{1,-1,i,-i\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3de2f39b465c89d2b275fcbf7608e6b29183fe8f)




































































![{\displaystyle \mathbf {\mathbb {Z} [i]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f233634501f262b44bc1c52382890258e538c2c)




















![{\displaystyle D=Z[{\sqrt {-5}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1cf26643a6585c825e6b1352a99d75d76c5f136)

![{\displaystyle D=Z[{\sqrt {-5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c915a53552cab85224c7003bb80697aba4726312)































![{\displaystyle \mathbb {Z} [(1+{\sqrt {-19}})/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49349e5a522b8fe9fe4cb4fb297ef30c3dbb9a06)
![{\displaystyle \mathbb {Z} [\omega ]=\{a+b\omega :a,b\in \mathbb {Z} ,\omega =(-1+i{\sqrt {3}})/2\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/554d4dfbaeb4bd42e5d36de7de88e053740cdd1c)







































































































































![{\displaystyle [a]=[a']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d536eab9633152e7551010d8676dcd6dc42249)
























![{\displaystyle [b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e016d81a1b29bb79b275e446042b925b7dd6b6d7)
![{\displaystyle x\in [a]\cap [b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87f4ad2e545b68ce32364bc604f11acb042cd09d)
![{\displaystyle x\in [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27ef3fb924e56d35478cdd6157a9bd842ca3aaf)



![{\displaystyle a\in [b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8abb5047c33633d5a0697408f3df2aead151e4ea)
![{\displaystyle b\in [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd1c441d4221216c8947ac50d43331042f72672b)

![{\displaystyle y\in [b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efde430c29cd5af74db44a270be12531cdb3f6f2)
![{\displaystyle [b]\subset [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cdb669f8b342f7ab3d8f5948fdaf179dddcafdd)












































































































































































![{\displaystyle [[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5891cd5afb04a8c63110dff73848a9c06b8c91ff)







![{\displaystyle [[B]]=[[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c44576f47c101dcf48b957f21709d80d1cc9b176)



















![{\displaystyle [[B]]\neq [[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399fee83340b8913a1039b09d273e776f5bcd7a3)










![{\displaystyle \ell =A+[[D]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/762f72ac07efbc2077f4937183491ee901e73dbb)
![{\displaystyle \ell =A+[[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f94387ab3d974cffed90053be68896753ba7bd5)


![{\displaystyle [[D']]=[[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3878e599cb12494e97284f4a678abf078a043b22)






![{\displaystyle B+[[D]]=A+[[D]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd39794a8546640dcac536d0e9a863555c3d8b3)
![{\displaystyle \ell _{A,B}=A+[[B-A]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb26e8861a2a3fc9e39aa9cf60e8e94062aa6cb2)
![{\displaystyle m=B+[[D]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/602bf1560c3afaf8eb01b6872bf932fbb57376c5)









![{\displaystyle m=(0,r/q)+[[1,(-p/q)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7efafdb921447868f98d1ce19980edb226b28b1f)

![{\displaystyle (r/p,0)+[[(0,1)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62f5a5b373ec0814aacd7046b875360cc2b2e3df)

















![{\displaystyle m=C+A+[[D]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24c934582af1f860a5a7d3b6491332d8f6fcb6f3)




















![{\displaystyle m=u(A)+[[u(D)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ec5d3a95a823b40562aae70fff1eeebf91c290)





















































































































![{\displaystyle \ell =[[P]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25bfe4296302b5ccc6fef57b667c09feffe8a4d7)






![{\displaystyle |G|=[G:C(g)]|C(g)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/add2b60309f17757c86836e6a3fb7e2f13b492ec)


![{\displaystyle [G:C(g)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe49e38343696923ea8812a887822d60f776f1df)
![{\displaystyle \sum _{|g^{G}|>1}[G:c(g)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec6e930696dfdec2f25a730ddacf3bae8dbdfbe8)
![{\displaystyle |G|=|Z(G)|+\sum _{|g^{G}|>1}[G:C(g)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ff5e13a04b8f654717c4f8e0e2c5aa67cc36cc)

























![{\displaystyle |\mathrm {fij} (G/P)|\equiv [G:P]\,(\mathop {\mbox{mód}} p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/624ae54250684ef8237a3a9b608f69061ce28357)
![{\displaystyle [G:P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d9b140b647d80194dc6fcc4e87457b12f16240b)

















![{\displaystyle [G:N_{G}(P)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69f6c380f12b8b38c5974ebbf0f09643135f701a)
![{\displaystyle |\mathrm {Syl} _{p}(G)|=[G:N_{G}(P)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb52403d3d7e48153033ae8c9118a221dd9bed7a)
