Ábaco Oriental/Métodos del Ábaco Moderno/División Moderna

Introducción y primeros métodos

División euclidiana

Si consideramos dos números naturales $a$ y $b$ , la división de $a$ por $b$ (indicado como $a/b$ o $a\div b$ ) responde a la pregunta de cuántas veces el número $b$ está contenido en el número $a$ . El número $a$ en $a/b$ es el dividendo y $b$ el divisor. La respuesta o resultado $q=a/b$ se denomina cociente.

Tomemos $a=1225$ y $b=35$ como ejemplo. No hay forma más sencilla de proceder para responder a la pregunta que mediante la resta repetida, contando el número de veces que podemos restar el divisor del dividendo. Podemos hacerlo directamente sobre el ábaco usando una columna como contador:

1225÷35 = 35, primera forma
Ábaco	Comentario
ABCDEFGHIJKL
35 1225
+1 -35	Restar 35 de KL, sumar 1 al contador en F
35 1 1190
+1 -35	Restar 35 de KL, sumar 1 al contador en F
35 2 1155
+1 -35	Restar 35 de KL, sumar 1 al contador en F
35 3 1120
...	Continuar 33 veces mas del mismo modo...
35 33 70
+1 -35	Restar 35 de KL, sumar 1 al contador en F
35 34 35
+1 -35	Restar 35 de KL, sumar 1 al contador en F
35 35 00	Hecho!, el cociente es 35 en EF

Así descubrimos que el número $35$ está contenido exactamente $35$ veces en $1225$ , ya que no podemos continuar restando $35$ sin empezar a tratar con números negativos. Por lo tanto, en este ejemplo, el cociente es: $q=35$ .

Como podemos ver, en este caso podemos escribir $1225=35\times 35$ , o bien:

$a=q\times b$

lo que no podemos esperar en el caso general. Si repitiéramos el proceso con $a=1240$ , veríamos que después de restar $35$ por $35$ nos quedaría $15$ en el ábaco, del que no podríamos seguir restando $35$ sin introducir números negativos. Por lo tanto, tenemos que $1240=35\times 35+15$ ; es decir, el resultado de dividir $1240$ por $35$ da un cociente de $35$ dejando un resto de $15$ . En general tendremos:

$a=q\times b+r$

dónde:

$a$ : dividendo
$b$ : divisor
$q$ : cociente
$r$ : resto

En el caso de que el resto sea cero, decimos que la división es exacta y el dividendo es un múltiplo del divisor.

Este es el concepto de división euclidiana para números naturales a la que se puede reducir la división de números con fracciones decimales sin más que multiplicar $a$ y/o $b$ por potencias de 10 adecuadas y después ajustar el punto decimal en el resultado.

Algunas mejoras: métodos de división a trozos

El procedimiento seguido en la sección anterior es el más simple posible conceptualmente, pero es extraordinariamente largo e ineficiente. En lugar de comenzar directamente restando el divisor $b$ ( $35$ ) del dividendo, comencemos preguntando qué potencia de 10 veces el divisor podemos restar del dividendo; en nuestro caso: ¿podemos restar 3500, 350 o solo 35? Claramente podemos restar 350 y comenzaremos a restar trozos de 350 , y cuando no podamos continuar, comenzaremos a restar trozos de 35 de la siguiente manera:

1225÷35 = 35, una gran mejora
Ábaco	Comentario
ABCDEFGHI
35 1225	Comienzo, contador en D
35 1 875	Restar 35 de GH, sumar 1 al contador D
35 2 525	Restar 35 de GH, sumar 1 al contador D
35 3 175	Restar 35 de GH, sumar 1 al contador D
35 31140	Restar 35 de HI, sumar 1 al contador E
35 32105	Restar 35 de HI, sumar 1 al contador E
35 33 70	Restar 35 de HI, sumar 1 al contador E
35 34 35	Restar 35 de HI, sumar 1 al contador E
35 35 00	Restar 35 de HI, sumar 1 al contador E
35 35	Sin resto, hecho!. El cociente es 35

Lo cual ha sido mucho más rápido. Como ve en el proceso anterior, hemos reducido intencionadamente la distancia entre el contador y el dividendo tanto como nos ha sido posible. Esto quizás oscurezca un poco el proceso, pero nos acerca a lo que haremos habitualmente con el método de división moderno que explicamos más abajo. Estudie el cálculo anterior cuidadosamente usando su propio ábaco. El método de división que hemos seguido aquí es el usado por las calculadoras mecánicas que mencionamos en el capítulo dedicado a la multiplicación.

Continuemos desde aquí buscando aún más eficiencia.

Si podemos duplicar fácilmente el divisor y retenerlo en la memoria, podemos acortar la operación restando trozos de una o dos veces el divisor.

Veces	Trozo
1	35
2	70

1225÷35 = 35, algo más sofisticado
Ábaco	Comentario
ABCDEFGHI
35 1225	Comienzo, contador en D
35 2 525	Restar 70 de GH, sumar 2 al contador en D
35 3 175	Restar 35 de GH, sumar 1 al contador en D
35 32105	Restar 70 de HI, sumar 2 al contador en E
35 34 35	Restar 70 de HI, sumar 2 al contador en E
35 35 00	Restar 35 de HI, sumar 1 al contador en E
35 35	Sin resto. Hecho, El cociente es 35

O incluso mejor si podemos construir una tabla como la de abajo doblando el divisor tres veces^[1]:

Veces	Trozo
1	35
2	70
4	140
8	280

1225÷35 = 35, un método muy efectivo
Ábaco	Comentario
ABCDEFGHI
35 1225	Comienzo, contador en D
35 2 525	Restar 70 de GH, sumar 2 al contador en D
35 3 175	Restar 35 de GH, sumar 1 al contador en D
35 34 35	Restar 140 de HI, sumar 4 al contador en E
35 35 00	Restar 35 de HI, sumar 1 al contador en E
35 35	Sin resto. Hecho, El cociente es 35

que es algo más corto y, claramente, nada podría ser más rápido que tener una tabla de multiplicar completa del divisor.

Tabla de multiplicación del divisor

Si disponemos de la tabla de múltiplos del divisor, en nuestro caso 35

Tabla de multiplicar por 35
Veces	Trozo
1	35
2	70
3	105
4	140
5	175
6	210
7	245
8	280
9	315

entonces podemos abreviar las cosas aún más.

1225÷35 = 35, el método más corto
Ábaco	Comentario
ABCDEFGHI
35 1225	Comienzo, contador en D
35 3 175	Restar 105 de GH, sumar 3 al contador en D
35 35 00	Restar 175 de HI, sumar 5 al contador en E
35 35	Resto nulo. Hecho, el cociente es 35

No hay duda, este es un método de división óptimo, ya que nada puede ser más rápido y cómodo... una vez que tengamos una tabla como la de arriba. Pero calcular la tabla de multiplicar de un divisor lleva tiempo, requiere papel y lápiz para anotarla y este trabajo adicional sólo estaría justificado si tenemos una gran cantidad de divisiones por hacer con el mismo divisor común.

En 1617 John Napier (Neper), el padre de los logaritmos, presentó un invento para aliviar este problema que consiste en una serie de tablillas, conocidas como ábaco neperiano o tablas neperianas, con la tabla de multiplicar de un dígito escrita en ellos y que podían combinarse para obtener la tabla de multiplicar de cualquier número. Por ejemplo, en nuestro caso

Tabla de multiplicar por 35 usando las tablas neperianas
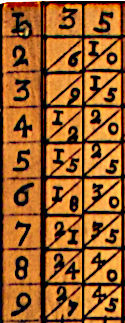
	1	35
	2	70
	3	105
	4	140
	5	175
	6	210
	7	245
	8	280
	9	315

No hay duda de que tal invento se extendió muy pronto a Oriente de mano de los misioneros Jesuitas^[2] y se usó junto con el ábaco, pero este uso debe considerarse excepcional; no todo el mundo tenía tablillas neperianas al alcance de la mano. Se necesita otra herramienta y esa herramienta es la tradicional tabla de multiplicar de 1 dígito que se aprende de memoria y que vamos a usar como aproximación a la tabla de multiplicar específica del divisor (la que se usó arriba), esta tabla nos guiará para elegir el dígito del cociente que debemos probar.

Cabe señalar que los procedimientos anteriores no agotan las posibilidades de los métodos de división por trozos^[3].

División moderna

División moderna vs tradicional

El método moderno de división se llama así porque, a lo largo de la primera mitad del siglo XX, su uso ha desplazado al del método tradicional, pero de hecho es mucho más antiguo que éste, habiendo sido desplazado por él en el siglo XIII. Una característica del método moderno es el uso de la tabla de multiplicar de 1 dígito como guía para la elección de la cifra provisional que tenemos que probar como cociente y para el cálculo del trozo que tenemos que restar del dividendo.

Tabla de multiplicar decimal
×	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

En comparación, el método tradicional utiliza tanto una tabla de división especial como guía para la cifra provisional del cociente como la tabla de multiplicar para calcular la parte a sustraer.

La razón principal por la que el método moderno comenzó a desplazar al método tradicional en Japón, después de la Restauración Meiji, es que puede ser aprendido de manera más fácil y rápida por quienes ya saben dividir con papel y lápiz al no requerir la memorización de una compleja tabla de división. Por otro lado, anticipemos que el método tradicional hace de la división un proceso completamente automatizado, sin necesidad de pensar; solo hay que seguir las reglas para obtener el resultado, lo que permite realizar la operación sin ningún cansancio mental. Trataremos sobre esta división tradicional el la sección de este libro dedicada a los métodos tradicionales.

Punto clave de la división con el ábaco

Uno de los puntos clave del aprendizaje del ábaco es ser conscientes de que este instrumento nos permite corregir algunas cosas de forma muy rápida y sin dejar rastros, lo que convierte al ábaco en un instrumento especialmente indicado para procedimientos de prueba y error. Esto nos es especialmente útil en el caso de la división. Si tenemos que dividir $634263\div 79283$ , en lugar de forzar nuestra mente tratando de encontrar la cifra correcta del cociente, simplemente elegimos una cifra aproximada provisional o interina simplificando el problema original a $63\div 7$ y la probamos intentando restar el trozo (cociente provisional)✕79283 del dividendo; al hacerlo, ocurrirá una de las siguientes situaciones:

El dígito del cociente intermedio es correcto: es decir, podemos restar el fragmento (dígito del cociente intermedio) ✕ (divisor), pero no podemos restar el cociente una vez más porque el resto es menor que el divisor.
Es insuficiente y debemos revisarlo al alza: podemos restar el fragmento (dígito intermedio del cociente) ✕ (divisor), pero aún podemos restar el cociente una vez más porque el resto es mayor o igual que el divisor. Agregamos uno al cociente intermedio y restamos el divisor nuevamente del resto.
Es excesivo y debemos revisarlo a la baja.: esta es la situación más compleja y propensa a errores. Por lo general, descubrimos demasiado tarde (en medio de la resta de fragmentos) que la cifra intermedia es excesiva y tenemos que retroceder, restar uno del cociente y restaurar el dividendo/resto agregándole lo que se le ha restado en exceso antes de que podamos seguir.

Por tanto, el proceso de obtención de un dígito del cociente tiene dos fases (prueba y error):

Elegir un dígito de cociente provisional.
Probar si es correcto y modificarlo si no lo es.

Una vez que hayamos encontrado la cifra correcta, generalmente tendremos un resto distinto de cero que actuará como dividendo si queremos extender la división al siguiente dígito del cociente.

Veremos todo esto a lo largo de los ejemplos que siguen, pero primero, necesitamos algunas palabras sobre cómo organizar la división en el ábaco.

Disposición en el ábaco de la división moderna

El dividendo es el término activo con el que vamos a trabajar en el ábaco, el divisor es inactivo y permanecerá invariable durante la operación, de hecho no es imprescindible introducirlo en el ábaco pero sí recomendable, especialmente para los principiantes. Como en el caso de la multiplicación, existen dos estilos para colocar dividendo y divisor en el ábaco, cada uno con sus ventajas y desventajas. Siéntase libre de probar ambas formas.

Disposición tradicional china

El divisor se sitúa en el extremo derecho del ábaco mientras que el dividendo se coloca hacia la izquierda, dejando al menos dos columnas libres a su izquierda.

**1225÷35 Disposición al estilo chino**
A	B	C	D	E	F	G	H	I	K	J	L	M

		1	2	2	5						3	5

Disposición tradicional japonesa

El divisor va al extremo izquierdo del ábaco mientras que el dividendo se sitúa a su derecha, dejando al menos cuatro columnas libres entre los dos términos.

**1225÷35 Disposición al estilo japonés**
A	B	C	D	E	F	G	H	I	K	J	L	M

3	5					1	2	2	5

En este capítulo usaremos el estilo japonés para los ejemplos, pero siéntase libre de probar ambos.

Colocando la cifra del cociente

La cifra del cociente intermedio se coloca en una de las dos columnas directamente a la izquierda del dividendo. Para decidir en cuál, necesitamos comparar el divisor con un número igual de cifras de los primeros dígitos del dividendo, agregando ceros a su derecha si fuera necesario; llamemos a estas cifras el dividendo de trabajo:

Dividendo de trabajo mayor o igual que el divisor: esto significa que el divisor cabe en el dividendo de trabajo y el cociente, es decir, el número de veces que el divisor entra en el dividendo de trabajo, se sitúa en la segunda columna a la izquierda del primer dígito del dividendo; Ejemplo: 827÷46. El dividendo de trabajo 82 es mayor que el divisor 46, luego el cociente intermedio va a la segunda columna a la izquierda del dividendo. La tabla de multiplicar sugiere que usemos 2 como cociente provisional (simplificando 827÷46 a 8÷4)

827÷46
Ábaco	Comentario
ABCDEFGHIJKLM
46 827
46 2 827	Situamos el cociente provisional 2 en E

Dividendo de trabajo menor que el divisor: esto significa que el divisor no cabe en el dividendo de trabajo. En este caso, necesitamos incluir el siguiente dígito del dividendo, o un cero si no quedan más, en nuestro dividendo de trabajo, y el cociente, el número de veces que el divisor entra en este dividendo de trabajo ampliado, se sitúa en la columna directamente a la izquierda del primer dígito del dividendo; Ejemplo: 18÷467, el dividendo de trabajo 180 es menor que 467, entonces lo ampliamos a 1800 y el cociente provisional se situará en la primera columna a la izquierda del dividendo. La tabla de multiplicar sugiere que usemos 4 como cociente intermedio después de simplificar 1800÷467 a 18÷4.

Caption text
Ábaco	Comentario
ABCDEFGHIJKLM
467 18
467 418	Situamos el cociente provisional 4 en G

Ejemplos

Debe comenzar haciendo ejercicios con divisores de un solo dígito y luego probar con divisores de dos, tres, etc. cifras. Con divisores de un dígito, nunca debería tener que revisar al alza o la baja. Por ejemplo, empiece por dividir 123456789 por los dígitos 2, 3, ..., 9. Veamos la división por 9 aquí.

Ejemplo: 123456789÷9 = 13717421

Por favor lea el símbolo "->" como: "la tabla de multiplicar sugiere usar ...".
Como verá, en todos los casos excepto en el último, el dividendo de trabajo es menor que el divisor y necesitamos expandirlo a dos dígitos.

123456789÷9 = 13717421
Ábaco	Comentario
ABCDEFGHIJKLMNO
9 123456789	12/9 -> 1 como cociente provisional
9 1123456789	situar cociente prov. en E
-9	restar 9✕1=9 de FG
9 1 33456789	33/9 -> 3 como cociente provisional
9 1333456789	situar cociente prov. en F
-27	restar 9✕3=27 de GH
9 13 6456789	64/9 -> 7 como cociente provisional
9 1376456789	situar cociente prov. en G
-63	restar 9✕7=63 de HI
9 137 156789	15/9 -> 1 como cociente provisional
9 1371156789	situar cociente prov. en H
-9	restar 9✕1=9 de IJ
9 1371 66789	66/9 -> 7 como cociente provisional
9 1371766789	situar cociente prov. en I
-63	restar 9✕7=63 de JK
9 13717 3789	37/9 -> 4 como cociente provisional
9 1371743789	situar cociente prov. en J
-36	restar 9✕4=36 de KL
9 137174 189	18/9 -> 2 como cociente provisional
9 1371742189	situar cociente prov. en K
-18	restar 9✕2=18 de LM
9 1371742 9	9/9 -> 1 como cociente provisional
9 13717421 9	situar cociente prov. en L
-9	restar 9✕1=9 de MN
9 13717421	Resto nulo, hecho! 123456789÷9 = 13717421

123456789 es un número curioso, es precisamente el producto de 9 por 13717421, ¡un número primo grande!

Ejemplo: 1225 ÷ 35 = 35 Divisor de dos dígitos. Revisando al alza y a la baja

1225÷35 = 35
Ábaco	Comentario
ABCDEFGHIJ
35 1225	12÷3↦4 como cociente provisional
+4	situar cociente prov. en F
35 41225	Tratar de restar 4✕35 de GHI,
-12	primero 4✕3 de GH
35 40025	ahora 4✕5 de HI
-20	¡No se puede!
-1	Revisar a la baja la cifra del cociente
35 30025
+3	Devolver lo sustraido en exceso de GH^[1]
35 30325
-15	continuar normalmente: restar 3✕5 de HI
35 3 175	17÷3↦5 como cociente provisional
+5	situar cociente prov. en G
35 35175	Tratar de restar 5✕35 de HIJ
-15	primero 5✕3 de HI
35 35025
-25	ahora 5✕5 de IJ
35 35	Resto nulo, fin! 1225÷35 = 35

Nota:

1

Hemos restado 4 × 3 = 12 de 'FGH' , pero si el dígito del cociente correcto es 3, deberíamos haber restado 3 × 3 = 9, por lo que restamos 3 en exceso (solo el primer dígito del divisor ). Debemos devolver este exceso antes de continuar.

Ahora, supongamos que después de nuestra "mala experiencia" revisando a la baja la primera cifra del cociente, y en exceso de prudencia, elegimos 4 como segundo cociente provisional en lugar de 5 como sugiere la tabla de multiplicar. Esta sería la continuación:

1225÷35 = 35, segundo dígito del cociente, ejemplo de revisión al alza
Ábaco	Comentario
ABCDEFGHI
35 3 175	17÷3 -> 5, pero usaremos 4 4!
+4	situar cociente prov. en G
35 34175	Tratamos de sustraer 4✕35 de HIJ
-12	primero 4✕3 = 12 de HI
-20	ahora 4✕5 = 20 de IJ
35 34 20	¡Resto mayor o igual al divisor!
+1	Revisar al alza G
-20	restar divisor del resto HI
35 34	Resto nulo, fin! 1225÷35 = 35

Ejemplo 1÷327

Hasta ahora hemos considerado divisiones entre números naturales con cocientes y residuos, así como números naturales, pero podemos operar con números decimales exactamente como lo hacemos en el cálculo escrito con división larga. Por ejemplo, encontremos el inverso de 327; es decir, 1/327 en un ábaco con 13 columnas.

1÷327 = 0.00305810...
Ábaco	Comentario
ABCDEFGHIJKLM
327 1	10/3 -> 3 como cociente provisional
327 31	situar cociente prov. en G
-09	restar 3✕3=9 de HI
327 3 1
-06	restar 3✕2=6 de IJ
327 3 4
-21	restar 3✕7=21 de JK
327 3 19	19/3 -> 6 como cociente provisional
327 30619	situar cociente prov. en I
-18	restar 6✕3=18 de JK
327 306 1
-12	no se puede restar 6✕2=12 de KL!
-1	revisar a la baja I
+3	restaurar el exceso sustraido de JK
327 305 4
-10	continuar normalmente, restar 5✕2=10 de KL
327 305 30
-35	restar 5✕7=35 de LM
327 305 265	36/3 -> 8 como cociente provisional
327 3058265	situar cociente prov. en J
-24	restar 8✕3=24 de KL
327 3058 25
-16	restar 8✕2=16 de LM
327 3058 9	Resultado hasta aquí: 3058

Hemos obtenido $3058$ como los primeros dígitos de $1/327$ , pero $1/327\approx 1/300=1/(3\cdot 100)=(1/3)\cdot 0.01\approx 0.33\cdot 0.01=0.0033$ por lo que nuestro resultado es en realidad $0.003058$ . Mas abajo daremos una regla para encontrar la varilla unidad de la división.

Ejemplo: 634263 ÷ 79283 = 7,999987 ..., un caso complicado

Finalmente, obtengamos el primer dígito del cociente de esta división especialmente maliciosa.

634263÷79283 = 7,999987...
Ábaco	Comentario
ABCDEFGHIJKLM
79283 634263	63/7 -> Probamos 9
79283 9634263
-63	restar 9*7=63 de HI
79283 9004263
-81	no se puede restar 9*9=81 de IJ!
-1	revisar D a la baja
+7	restaurar lo restado en exceso del dividendo
79283 8 74263
-72	continuar restando 8x9=72 de IJ
79283 8 02263
-16	restar 8*2=16 de JK
79283 8 00663
-64	restar 8*8=64 de KL
79283 8 00023	no se puede restar 9*3=27 de LM!
-1	revisar D a la baja
+7928	restaurar lo restado en exceso del dividendo
79283 7 79303
-21	continuar restando 7x3=21 de LM
79283 7 79282	cociente: 7, resto: 79283

No hay duda de que en este caso redondear el divisor 79283 a 80000 nos habría dado mejores resultados ya que 63÷8 sugiere usar 7 (la cifra correcta) como dígito del cociente provisional.

634263÷79283 = 7,999987..., divisor redondeado
Ábaco	Comentario
ABCDEFGHIJKLM
79283 634263	63/8 -> probamos 7
7634263
-49	restar 7*7=49 del dividendo HI
79283 7144263
-63	restar 7*9=63 del dividendo IJ
79283 7 81263
-14	restar 7*2=14 del dividendo JK
79283 7 79863
-56	restar 7*8=56 del dividendo KL
79283 7 79303
-21	restar 7*3=21 del dividendo LM
79283 7 79282	cociente: 7, resto: 79283

La varilla unidad y los decimales

La contrapartida de la regla para encontrar la varilla unidad en el caso de la multiplicación es la siguiente regla para la división:

La columna de las unidades de los cocientes se ubica $n+1$ columnas a la izquierda de la columna de las unidades del dividendo; donde $n$ es el número de dígitos del divisor a la izquierda de su punto decimal (¡que puede ser negativo!).

La siguiente tabla muestra los valores de $n$ para algunos divisores:


Divisor	n
32.7	2
3.27	1
0.327	0
0.00327	-2

Ejemplo: 1/327 (lo hemos visto arriba)

1/327; columna unidad
Ábaco	Comentario
ABCDEFGHIJKLM
327 1	el divisor tiene 3 dígitos. n=3
.	varilla unidad del dividendo
...
327 3058 9	Fin de la división. Resultado: 3058
.	varilla unidad del dividendo
<---	desplazarla n+1 = 4 posiciones a la izquierda
.	varilla unidad del cociente
3058	por lo tanto, ésto...
.003058	... debe leerse: 0.003058

Multiplicación y división como operaciones inversas

En los cálculos escritos siempre podemos revisar nuestro trabajo para asegurarnos de que no hemos cometido errores y que el resultado obtenido es el correcto. En los cálculos con el ábaco esto no es posible ya que el ábaco no guarda memoria del pasado y de los resultados intermedios. Podemos recurrir a algunos artificios como la prueba del nueve o del once, pero la forma tradicional de verificar los resultados con el ábaco ha sido repetir los cálculos o deshacerlos.

Deshacer sumas y restas es tan simple como partir del resultado y restar lo que hemos sumado y sumar lo que hemos restado; Si hacemos tanto el cálculo como la verificación correctamente, deberíamos terminar con un ábaco limpio, puesto a cero. Para verificar una multiplicación usaremos la división y, recíprocamente, para verificar una división usaremos la multiplicación, sumando el resto si lo hay. Después de hacer esto, devolveremos el ábaco a su estado inicial con los dos operandos originales en sus posiciones de partida. Veamos un ejemplo:

Comprobando 2461÷64 por multiplicación
Ábaco	Comentario
ABCDEFGHIJ
64 2461	24/6 -> 4 como cociente provisional
42461	situar cociente prov. en F
-24	restar 4✕6=24 del dividendo GH
64 4 61
-16	no se puede restar 4✕4=16 del dividendo HI
-1	revisar cociente a la baja
64 3 61
+6	restaurar lo restado en exceso del dividendo GH
64 3 661
-12	continuar normalmente, restar 3✕4=12 del dividendo HI
64 3 541	54/6 -> 9, pero vamos a usar 8
64 38541
-48	restar 8✕6=48 del dividendo HI
64 38 61
-32	restar 8✕4=32 del dividendo IJ
64 38 29	cociente: 38, resa 29
	La revisión por multiplicación empieza aquí
+48	sumar 8✕6=48 a HI
64 38509
+32	sumar 8✕4=32 a IJ
64 38541
64 3 541	borrar G
+18	sumar 3✕6=18 a GH
64 32341
+12	sumar 3✕4=12 a HI
64 32461
64 2461	borrar F. Estado inicial!

En este libro se ha sugerido usar el número 123456789 para sus primeros ejercicios tanto de multiplicación como de división por un solo dígito. Intente combinarlos con la operación inversa; por ejemplo: divida 123456789 por 9 para obtener 13717421 y multiplique este resultado por 9 para que 123456789 vuelva a la misma posición inicial en el ábaco. O bien comience multiplicando 123456789 por 9 para obtener 1111111101 y luego divida este resultado por 9 para volver al punto de partida. Pruebe todos los dígitos del 2 al 9. Es un buen ejercicio de rutina.

Referencias

↑ Wilson, Jeff. «Long Division Teaching Aid, "Double Division"». Double Division. Archivado desde el original, el March 02, 2021.
↑ *Michael R. Williams, Michael R. (1990). «Early Calculation». En Aspray, William. Computing Before Computers. Iowa State University Press,. ISBN 0-8138-0047-1. http://ed-thelen.org/comp-hist/CBC.html.
↑ «The Definitive Higher Math Guide on Integer Long Division (and Its Variants)». Math Vault. Archivado desde el original, el May 14, 2021.

Recursos externos

Hojas de ejercicios

«The generator». Practicing the soroban.

Otras lecturas

«Division». The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle Co., Inc.. 1954. ISBN 978-0-8048-0278-9. https://archive.org/details/japaneseabacus00taka/page/64/mode/2up.
Heffelfinger, Totton (2004). «Division». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el June 29, 2021.
Siqueira, Edvaldo (2004). «Decimals & Division». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el May 6, 2021.

Ábaco Oriental

▶[+6] Índice, Introducción, Página de edición, Enlaces, Texto completo

La humanidad ha utilizado ábacos, de un tipo u otro, desde los albores de la civilización para satisfacer sus necesidades de cálculo y contabilidad. La versión moderna del ábaco oriental, originario de China, todavía se utiliza hoy en día en todo el mundo para ayudar a los niños a mejorar su comprensión y habilidades numéricas. La Aritmética con Cuentas (珠算; léase zhūsuàn en chino, shuzan en japonés), o arte del uso del ábaco oriental, ha sido inscrito en 2013 en la Lista Representativa del Patrimonio Cultural Inmaterial de la Humanidad de la UNESCO.▶

{{Ábaco Oriental}}/◇

[IDchunk-1] Wilson, Jeff. «Long Division Teaching Aid, "Double Division"». Double Division. Archivado desde el original, el March 02, 2021.

[2] *Michael R. Williams, Michael R. (1990). «Early Calculation». En Aspray, William. Computing Before Computers. Iowa State University Press,. ISBN 0-8138-0047-1. http://ed-thelen.org/comp-hist/CBC.html.

[3] «The Definitive Higher Math Guide on Integer Long Division (and Its Variants)». Math Vault. Archivado desde el original, el May 14, 2021.

[1]

[2]

[3]